
Наврозов, В. В. Элементы высшей математики 1
.pdfМИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«Вятская государственная сельскохозяйственная академия» Кафедра математики
В.В. Наврозов, Т.В. Малых
Элементы высшей математики 1
Дифференциальное исчисление
Учебное пособие для студентов биологического факультета
Киров 2012
УДК 517.2 ББК 22.161.11
Наврозов В.В., Малых Т.В. Элементы высшей математики 1. Дифференциальное исчисление: Учебное пособие для студентов биологического факультета. – Киров: ФГБОУ ВПО Вятская ГСХА, 2012.- 42с.
Рецензенты: доцент кафедры математики Вятской ГСХА, кандидат физикоматематических наук Фарафонов В.Г.; доцент кафедры математического моделирования в экономике ВятГУ, кандидат физикоматематических наук Ковязина Е.М.
Учебное пособие рассмотрено и утверждено методической комиссией инженерного факультета Вятской государственной сельскохозяйственной академии (протокол № 8 от 3 мая 2012 г.).
В учебном пособии рассмотрены основные понятия дифференциального исчисления. Приведены примеры решения задач, задания для самостоятельной работы и контрольные задания.
ФГБОУ ВПО Вятская ГСХА , 2012
Наврозов Виктор Васильевич, Малых Татьяна Викторовна, 2012
2
Оглавление
1.Производная функции…………………………………………........4
2.Геометрические приложения производной……………………….8
3.Производные высших порядков…………………………….........10
4.Дифференциал функции. Приложение дифференциала к приближенным вычислениям……………………………………….12
5.Правило Лопиталя…………………………………………...…….15
6.Исследование функций с помощью производных……………....18
6.1Возрастание и убывание функций. Точки экстремума………...18
6.2Наибольшее и наименьшее значения функции на отрезке…….23
6.3Выпуклость и вогнутость графика функции. Точки перегиба...25
6.4Асимптоты………………………………………………………...28
6.5Исследование функций и построение их графиков. Общая схема исследования функции…………………………………………….....31
Контрольные задания………………………...………………………37
3

1. Производная функции
Правила дифференцирования
U =U (x);V =V (x) − дифференцируемые функции аргумента х.
I. (U ±V )′ =U ′±V ′ |
II. |
|
IIа.(CU ) |
= CU , C − const |
III. |
′ |
′ |
|
(UV )′ =U ′V +UV ′
U |
′ |
|
|
′ |
′ |
|
|
= |
U V −UV |
|
|||
|
|
|
|
|
|
|
|
|
V 2 |
|
|||
V |
|
|
|
|
||
IV. Производная сложной функции.
y = f (u),u =ϕ(x) y = f (ϕ(x)) , тогда y′x = y'u u′x .
Производная сложной функции равна произведению производной внешней функции по внутреннему аргументу на производную внутренней функции по конечному аргументу.
V. Производная обратной функции.
y = y(x) x = x(y) x′(y)= y′1(x).
Формулы дифференцирования
|
|
|
|
|
|
|
|
′ |
|
8. y = cos x y′ = −sin x |
|
|
|
|
|||||||||
1. y =С−const y |
=0 |
|
|
|
|
|
|||||||||||||||||
|
|
α |
′ |
|
|
|
|
α−1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|||
2. |
y =x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
y |
=αx |
|
|
9. y = tgx y′ = |
cos2 |
|
|
x |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
x |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
3. y =a |
x |
y =a |
lna |
|
10. y = ctgx y′ = − |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
sin2 |
x |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
4. |
y = ex y′= ex |
|
|
|
|
11. y = arcsin x y |
′ |
= |
|
|
1 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − x2 |
||||||||||
5. |
y = loga х y′ = |
|
1 |
|
12. y = arccos x y′ = − |
1 |
|
||||||||||||||||
|
x ln a |
|
|
1 − x2 |
|||||||||||||||||||
6. y = ln x y′ |
1 |
|
|
|
|
13. y = arctgx y′ = |
|
|
|
1 |
|
|
|
|
|
||||||||
= |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
x |
|
|
|
|
|
|
1 + x2 |
|
|
||||||||||||||
7. |
y = sin x y′ = cos x |
|
14. y = arcctgx y′ = − |
|
1 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 + x2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
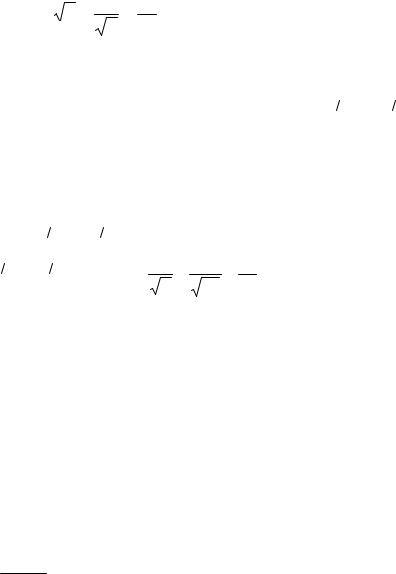
Примеры. Найти производные функций:
а) y = 3x2 + 2 x − 3 3x − x14 + 5 .
Решение. Вводя дробные и отрицательные показатели степени, преобразуем данную функцию: y = 3x2 + 2x1 2 − 3x−1 3 − x−4 + 5.
Применяя правило дифференцирования суммы функций и формулу 2 (см. стр.4), получим
y′ = (3x2 + 2x1 2 −3x−1 3 − x−4 +5)′ = 3(x2 )′ + 2(x1 2 )′ −3(x−1
2 )′ −3(x−1 3 )′ −(x−4 )′ +5′ =
3 )′ −(x−4 )′ +5′ =
6x + x−1 2 + x−4 3 + x−5 = 6x + |
1 |
+ |
1 |
+ |
4 . |
|
x |
|
3 x4 |
|
x5 |
б) y = x2 cos x.
Решение. Применяя правило дифференцирования произведения функций и формулы 2, 8 (стр.4), получим
y′ = (x2 cos x)′ = (x2 )′cos x + x2 (cos x)′ = 2x cos x − x2 sin x.
в) y = ex . arctgx
Решение. Применяя правило дифференцирования частного и формулы 4, 13 (стр.4), получим
|
ex |
′ |
|
(ex )′ arctgx − ex (arctgx)′ |
|
e |
x |
arctgx − |
|
ex |
|
|
ex (1 + x2 )arctgx − ex |
|
|||||||
|
|
|
1 |
+ x2 |
|
|
|
||||||||||||||
y′ = |
|
|
= |
|
|
|
= |
|
|
|
|
|
|
|
= |
|
|
|
|
|
. |
|
|
2 |
|
|
|
|
2 |
|
|
|
(1 + x |
2 |
)arctg |
2 |
|
||||||
|
|
|
|
arctg |
x |
|
|
|
arctg |
x |
|
|
|
x |
|
||||||
arctgx |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
5

|
|
3 |
|
|
2 |
|
г) |
y = x |
|
5x +1 |
− |
|
. |
|
|
|||||
|
|
|
|
|
3x |
|
Решение. Сначала раскроем скобки, затем дифференцируем как сумму функций.
|
|
y = 5x4 + x3 − |
2 x2 |
, |
|
|||
|
|
|
|
|
|
3 |
|
|
y′ = |
5x4 |
+ x3 − |
2 x2 |
′ |
= 20x3 |
+3x2 − |
4 x . |
|
|
|
|
3 |
|
|
|
|
3 |
д) |
y = xln x + |
3x |
. |
|
sin x |
||||
|
|
|
Решение. Здесь применим правило дифференцирования суммы функций (I), затем правила дифференцирования произведения (II) и частного (III).
|
|
|
|
|
x |
|
′ |
|
|
|
x ′ |
|
x |
|
′ |
|
|
|
|
|
|
|
|
||
|
|
|
3 |
|
|
= x′ln x + x(ln x)′ + |
(3 )sin x −3 (sin x) |
|
|
|
|
|
|
|
|
|
|||||||||
y′ = x ln x |
+ |
|
|
|
= ln x +1 + |
|
|
||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
sin |
2 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
+3x sin x ln 3 −cos x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
sin2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Упражнение 1. Найти производные функций: |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
1) |
y = 2x + |
|
3 −53 |
x + 7 ; |
2) y = x − 2 x ; |
|
|
3) y = 84 x − 4 x + 3 ; |
|||||||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4) |
y = 4cos x + 5ex ; |
|
5) |
y = 3x + x3 ; |
|
|
6) y = 2 ln x cos x ; |
|
|
||||||||||||||||
7) |
y = (3x − 2)tgx ; |
|
8) |
y = x2 arcctgx |
|
; 9) |
y = |
|
|
|
|
1 |
|
|
; |
||||||||||
|
|
x |
2 |
+ 5x + |
6 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
10) y = |
e |
|
; |
|
|
|
|
|
11) y = 1 + x ; |
|
|
12) |
|
y = |
|
x |
−3 |
; |
|
|
|||||
3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
+ 3 |
|
|
||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
x |
|
|
|
||
6
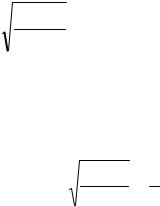
13) |
y = |
|
|
3x |
|
− arctgx ; 14) y = |
x |
; 15) |
y = |
|
e х |
|
. |
|
|
|
|
|
|
− x |
2 |
||||||
1 |
+ x |
2 |
sin x + cos x |
||||||||||
|
|
|
|
|
4 |
|
|
||||||
Примеры. Найти производные следующих функций:
а) y = (1 + 4x2 )3 .
Решение. Применяя правило функции (IV) и учитывая, что получаем
дифференцирования сложной
(1 + 4x2 )- внутренняя функция,
y′ = ((1 + 4x2 )3 )′ = 3(1 + 4x2 )2 (1 + 4x2 )′ = 24x(1 + 4x2 )2 .
б) y = ln tgx .
Решение. Применяя правило дифференцирования сложной функции и учитывая, что tgx − внутренняя функция, получаем
|
|
y′ = |
(ln tgx)′ = |
1 |
(tgx)′ = |
|
1 |
|
|
|
= |
|
|
2 |
|
|
. |
|
|
|
|
|||||||
|
|
|
tgx cos |
2 |
|
x |
|
sin 2x |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
tgx |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
в) y = ln 3 |
e2 x |
2 x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Прежде чем находить |
|
производную, |
|
|
функцию |
|||||||||||||||||||||||
преобразуем, используя правила логарифмирования: |
|
|
|
|
||||||||||||||||||||||||
|
y = ln 3 |
1 |
e2 x2 x |
= 1 [ln e2 x − ln(1 + e |
2 x )]= |
1 |
[2x − ln(1 + e2 x )]. |
|||||||||||||||||||||
|
|
|
+ e |
3 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[2x − ln(1 + e2 x )] |
′ |
|
|
|
|
2e |
2 x |
|
|
|
|
|
|
|
|
|
|
||||||||
|
y′ = 1 |
= 1 |
|
− |
|
= |
|
2 |
|
|
|
|
|
|||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||||
|
|
+ e |
2 x |
3(1 |
+ e |
2 x |
) |
|||||||||||||||||||||
|
|
3 |
|
|
|
|
|
3 |
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||
Упражнение 2. Найти производные функций:
7
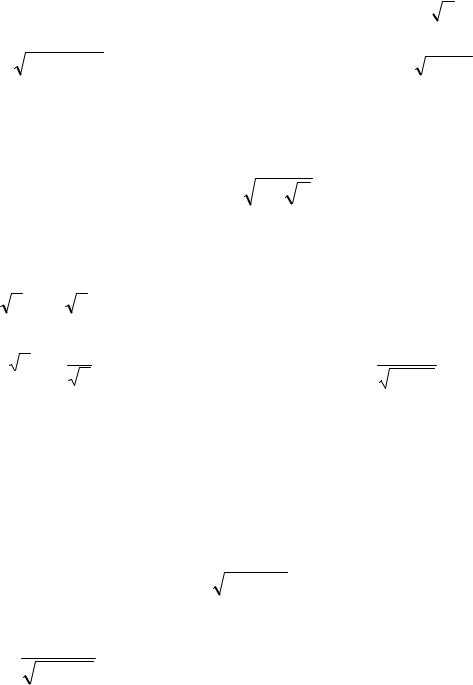
1) |
y = sin(3x − 5); |
|
2) |
|
y = e4 x+2 ; |
|
|
3) |
y = tg3 x ; |
|
|
|
|||||||||||||||||||
4) |
y = 5 x2 |
+ x +5 |
; |
|
5) y = ln cos 3x ; |
|
|
6) |
y = |
sin 2x ; |
|
|
|
||||||||||||||||||
7) y = cos |
2 |
4x ; |
|
|
|
8) y = ln |
3x2 |
; |
|
|
9) y = ln(5x2 + 6x +1); |
||||||||||||||||||||
|
|
|
|
1 − x2 |
|
|
|||||||||||||||||||||||||
10) |
y = arctg 1x ; |
|
|
|
11) y = |
1 + |
x ; |
|
12) y = sin5x cos |
x |
. |
|
|||||||||||||||||||
|
|
|
|
5 |
|
||||||||||||||||||||||||||
Упражнение 3. Найти производные функций: |
|
|
|
|
|
|
|
||||||||||||||||||||||||
1) y = x(x3 − x + 2)3 ; 2) y = 2x10x ; |
|
3) y = (x3 −3x + 2) (x4 + x −1); |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
tgx |
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
4) y = ( x + |
1) |
|
− |
1 |
; 5) |
y = |
|
|
; |
|
|
|
|
|
6) y = |
|
|
|
|
; |
|
|
|
|
|||||||
x |
|
x |
|
|
|
|
|
x2 + |
4 |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
7) y = |
2x4 |
; |
|
|
|
8) |
y = |
|
ex |
|
; |
|
|
9) y |
= |
x2 +1 |
; |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
5 + x |
2 |
|
|
|
|
|
|
|
|
|||||||||||||||
2 |
|
|
|
|
|
arctgx |
|
|
|
|
|
||||||||||||||||||||
|
|
9 − x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
10) |
y = arctgx2 ; |
|
11) |
y = arcsin |
5 |
; |
|
12) |
|
y = x ln(x3 − 6x); |
|
||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13) |
y = log2 (x2 +1); |
14) |
y = 1 + ln4 x ; |
|
15) |
y = |
1 |
|
|
; |
|
|
|
|
|||||||||||||||||
|
ln x |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
16) |
y = arccos x |
; |
|
17) |
y = cos2 x cos x2 |
; 18) |
y = ex sin x cos2 x |
. |
|
|
|||||||||||||||||||||
|
1 − 4x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
2. Геометрические приложения производной |
|
|||||||||||||||||||||||||
Значение производной f ′(x0 ) |
функции |
y = f (x) в точке x0 |
равно |
||||||||||||||||||||||||||||
тангенсу угла наклона касательной |
к графику функции в точке |
||||||||||||||||||||||||||||||
M (x0 ; f (x0 )), т.е. kτ |
= f ′(x0 ) . Тогда уравнение касательной к графику |
||||||||||||||||||||||||||||||
функции y = f (x) в точке M (x0 ; y0 = f (x0 )) |
будет следующим: |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
y − f (x0 )= f ′(x0 )(x − x0 ). |
|
|
|
|
|
|
|
|
|
|
(2.1) |
|||||||||||
или |
|
|
y −y0 = y0′(x −x0 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
, где y0 = f (x0 ), |
y0′ |
|
= f ′(x0 ). |
|
|
|
|
(2.2) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Нормаль − прямая, перпендикулярная касательной в точке
касания, поэтому kn = − |
1 |
и уравнение нормали к графику функции |
|||||
k |
|||||||
|
τ |
|
|
|
|
|
|
y = f (x) в точке M (x0 ; y0 ) |
следующее: |
|
|
|
|||
y −y =− |
1 |
(x −x |
) |
. |
(2.3) |
||
|
|||||||
|
|
0 |
y0′ |
0 |
|
||
|
|
|
|
|
|
|
|
Пример. Найти уравнения касательных, проведенных к параболе y =x2 −4:
а) в точке (−2;0) ;
б) в точках пересечения параболы с прямой x − y − 2 = 0 .
Решение.
а) x0 = −2, y0 = 0.
Для определения углового коэффициента касательной k , найдем производную функции y = x2 −4 и вычислим ее частное значение при x = −2:
y′ = (x2 −4)′ = 2x , тогда k = y0′ = y′(−2)=−4.
Подставляя значения x0, y0, y0′ в уравнение (2.2), получим уравнение касательной:
y = −4(x + 2) 4x + y +8 = 0 .
б) Точка пересечения принадлежит обеим линиям, поэтому координаты точки находим, решая систему уравнений:
|
2 |
−4, |
|
2 |
−4, |
A(2;0), B(−1;−3). |
y = x |
y = x |
|||||
|
|
|
|
|
||
x − y −2 =0. |
y = x −2. |
|
||||
|
|
|
|
|
9 |
|
Из предыдущей задачи |
y′ = 2x . Тогда |
угловой коэффициент |
|
касательной в точке A y0′ = 4 , в точке B y0′ |
= −2 . |
||
Уравнения касательных |
к |
параболе |
y = x2 −4 в точках |
пересечения с прямой x − y − 2 = 0 имеют следующий вид: |
|||
y = 4x +8 |
(в точке A(2;0) ), |
||
y = −2x −5 |
(в точке B(−1;−3) ). |
||
Упражнение 4.
1) Составить уравнения касательной и нормали к графику функции
y = 2x3 − x 2 + 2 :
а) в точке, абсцисса которой х =1 ;
б) в точке пересечения с параболой y = −x2 .
2)В каких точках угловой коэффициент касательной к кубической параболе равен 1?
3)В какой точке касательная к параболе y = x2 …
а) параллельна прямой y = 4x −5 ;
б) перпендикулярна к прямой |
2x −6 y + 5 = 0 ; |
в) образует с прямой 3x − y +1 |
= 0 угол 450 ? |
3. Производные высших порядков |
|
Если y′ есть производная |
функции y = f (x) и y′ = f ′(x) − |
дифференцируемая функция, то производная от y′ называется
10
