Добавил:

fench Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Кузбасский государственный технический университет

Предмет:

Физика

Файл:

Методички / А.А. Колесникова Физика. Программа, методические указания к практическим занятия и контрольные задания по общему курсу физики для студентов заочной формы обучения специальностей 060808 и 060814

.pdf

Скачиваний:

Добавлен:

19.08.2013

Размер:

752.9 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

При изотермическом		(T = const) расширении
А =	m	RT ln	V2	=	m	RT ln	P1	.	(43)
	M
			V		M		P
		1					2
Количество теплоты, необходимое для нагревания вещества массой m
на ∆ Т кельвинов:		Q = m C ∆ T ,							(44)

где С - удельная теплоемкость вещества, которая зависит от характера нагревания: Ср - при постоянном давлении, Сv - при постоянном объеме.

i + 2

(45)

Первое начало термодинамики:

Q =

A +

∆ U .

(46)

Коэффициент полезного действия цикла Карно:

Q1 −

T1 − T2

(47)

где Q1 - количество тепла, полученное от нагревателя

с температурой T1;

Q2 - количество тепла, отданное холодильнику с температурой T2 .

2.2. Примеры решения задач

1. В сосуде объемом 3 м3 находится смесь 7 кг азота и 2 кг водорода при температуре 27° С. Определить давление и молярную массу смеси газов.

Дано:

V = 3 м3 m1 = 7 кг m2 = 2 кг

М1 = 28 10-3 кг/моль М2 = 2 10-3 кг/моль

Т= 300 К

Р- ? М - ?

Решение Запишем уравнение (34) для азота и

водорода:

Р V =		m1	RT ,	P V =	m2	RT,
Р V =			RT ,	P V =		RT,
1		M1		2	M 2
		M1			M 2
где Р1	и Р2 -		парциальные давления
азота и водорода.
Выразим	Р1	и	Р2:

	16
Р1 =	m1RT	,	P2	=	m2RT
Р1 =	M1V	,	P2	=	M 2V
	M1V				M 2V

и подставим их в уравнение (38) - закон Дальтона:

Р =

(

M1 M 2

8,31 300

Р =

(

) = 1,04 106

Па.

10− 3

2 10− 3

Молярную массу смеси газов найдем по формуле (39):

М =	(m1 +	m2 )M1M 2					= 7,2 10− 3 кг/моль.
	m M
		2	+	m	M	1
	1			2
Ответ : Р = 1,04 106 Па;				M = 7,2 10− 3 кг/моль.

2. Кислород массой 320 г нагревают при постоянном давлении от 300 до 310 К. Определить количество теплоты, поглощенное газом, изменение внутренней энергии и работу расширения газа.

Дано:

Решение

m = 320 г = 0,32 кг

Изменение внутренней энергии

Т1 =

300 К

газа

(40):

i m

Т2 =

310 К

∆

U =

2 M R∆ T ,

М =

32 10-3 кг/моль

Q − ? ÄU - ? A - ?

где i = 5 – число степеней свободы

двухатомных молекул.

∆ U =

0,32

8,31(310 −

300) =

2080 Дж .

2 0,32 10−

Работа расширения газа при изобарном процессе (42):

А =

Р ∆ V .

(P =

Запишем уравнение Менделеева-Клапейрона

(34) для двух состояний

const) :

PV =

RT ,

PV =

RT .

Почленным вычитанием находим:

P(V − V ) =

R(T

− T ).

		17
Следовательно:			m
	A =		m	R∆ T ,
	A =		M	R∆ T ,
	0,32		M
A =	0,32	8,31 10 = 830 Дж .
A =	0,32 10− 1	8,31 10 = 830 Дж .

Поглощенное газом количество теплоты найдем по первому началу

термодинамики (46):

Q = A + ∆ U ,

Q = 830 + 2080 = 2910 Дж .

Ответ: Q = 2910 Дж; U = 2080 Дж; A = 830 Дж.

3. Постоянный ток (задачи 21 - 30).

3.1. Законы постоянного тока. Основные формулы Закон Ома для однородного участка цепи:

I =	U	,	(48)
I =	R	,	(48)
	R
где I - сила тока; U - напряжение на участке цепи;			R - сопротивление уча-
стка.

Закон Ома для замкнутой цепи:

	I =	ε
			,
где ε		R + r
	- электродвижущая сила источника тока;
цепи;	r - внутреннее сопротивление источника.
	Сопротивление однородного проводника

(49)

R - сопротивление внешней

R =	ρ			l	,	(50)
R =	ρ			S	,	(50)
				S	l - длина;	S - площадь поперечного се-
где ρ - удельное сопротивление;					l - длина;	S - площадь поперечного се-
чения проводника.
Плотность тока		I
j =		I	.			(51)
j =			.			(51)
		S
Закон Ома в дифференциальной форме:
j =	γ E ,					(52)

18
где γ - удельная проводимость проводника (γ =			1	); Е	- напряженность
где γ - удельная проводимость проводника (γ =				); Е	- напряженность
поля в проводнике. E = U /l.			ρ
поля в проводнике. E = U /l.
Закон Джоуля-Ленца:	U 2
Q = IUt = I 2 Rt =	U 2	t,			(53)
Q = IUt = I 2 Rt =		t,			(53)
	R

где Q - количество теплоты, выделяющееся на однородном участке цепи

при прохождении тока за время t .

Работа тока эквивалентна количеству теплоты: А = Q.

A = IUt = I 2Rt =	U 2	t.

	R

Мощность, выделяющаяся на однородном участке цепи:

N = IU = I 2R =	U 2	.

	R

Мощность, выделяющаяся во всей цепи:

N =	Iε =	I 2 (R +	r) =	ε 2		.
				R +	r

Коэффициент полезного действия (КПД) источника тока:

η =	Nn	=	U	=	R	.
			ε		R + r
	N з

(54)

(55)

(56)

3.2. Примеры решения задач
1. В медном проводнике сечением				S =	6 мм2 и длиной l = 5 м те-
чет ток. За	1 мин	в проводнике выделяется			18 Дж	теплоты. Опреде-
лить напряженность поля, плотность тока и силу тока в проводнике.
Дано:					Решение
S = 6 10-6 м2			Силу тока	найдем из		закона Джоуля–
l = 5 м				Ленца (53):
t = 60 c				I =	Q	QS
Q = 18 Дж				I =	Rt =	ρ l t ,
ñ = 1,7 10-8 Ом м
Е − ?	j − ? I − ?

		19
I =	18 6 10−		6
	1,7	10− 8 5	= 4,6 A .
			60

Плотность тока j				по определению равна:
		j =		I	,	j =	4,6		= 7,7 105
							10−	6
				S		6
Напряженность поля определим из закона
альной форме (52):
E =	j	= j ρ	;			E = 7,7	105 1,7 10− 8 =

	γ

м2

Ома в дифференци-

1,3 10− 2 B/м.

Ответ: E = 1,3 10− 2 B/м; j = 7,7 105 A/м2; I = 4,6 A .

2. Внутреннее сопротивление аккумулятора r = 2 Ом. При замыкании его сопротивлением R1 сила тока I1 = 4 A, при замыкании сопротивлением R2 сила тока I2 = 2 A . Во внешней цепи в обоих случа-

ях выделяется одинаковая мощность. Определить ЭДС аккумулятора и внешние сопротивления R1 и R2.

Дано:

Решение

r = 2 Ом

Запишем закон Ома для замкнутой цепи:

I1 = 4 A

I1 =

I2 =

I2 = 2 А

R1 +

R2 +

N1 =

откуда следует:

ε − ?

R1 − ? R2 −

I1(R1 + r) = I2 (R2 + r).

Из равенства мощностей получаем

I 2 R

I 2R .

Решая совместно два последних уравнения, находим

R =

I2r

R =

I1r

R =

2 2

= 1Ом,

4 2

R =

4 Ом,

= I

(R + r),

ε = 4(1+ 2) = 12 B .

Ответ: ε =

12 В,

R1 = 1Oм;

R2 =

4 Oм.

3. ЭДС батареи равна 20 В. КПД батареи η = 0,8 при силе тока I = 4 А. Чему равно внутреннее сопротивление батареи?

Дано:

Решение

å=

20 В

Из формулы (56)

для КПД имеем

η =

0,8

ηε

I = 4 A

η =

R =

r −

Закон Ома для замкнутой цепи (49) позволяет

определить:

ε − IR = ε − Iηε

/ I = ε (1− η ) ,

r =

20(1−

0,8)

= 1Ом.

Ответ:

r = 1Ом.

4. Рассчитать стоимость электроэнергии, потребляемой телевизором за месяц, если он включается ежедневно на 2 ч; мощность телевизора 60 Вт, цена 10 к. за 1кВт ч.

Дано:		Решение
t =	2 30 ч	Потребляемую электроэнергию находим
N =	60 Вт = 60 10-3 кВт	по формуле
Ц =	10 к./кВт ч	W = N t ,

S - ?

где N – мощность электроприбора; t – время его работы.

Стоимость электроэнергии равна

S = W Ц ,

S = N t Ц, S = 60 60 10 10− 3 = 36 к.

Ответ: S = 36 к.

4. Магнитное поле тока. Явление электромагнитной индукции (задачи 31 – 40)

4.1. Основные законы и формулы

Связь между индукцией магнитного поля и напряженностью:
!	!
В =	µ µ 0 Н .	(57)

Закон Био–Савара–Лапласа:


dB = µµ	0		Idl				→	→
			Idl		sin (I dl,			r ) ,	(58)
					sin (I dl,			r ) ,	(58)
4π			r 2
где dB – модуль вектора магнитной индукции поля, созданного
током I в проводнике длиной dl				на расстоянии r от dl ;					- магнит-
ная проницаемость среды; µ 0 =		4π		10− 7 Гн/м – магнитная постоянная.
На основе формулы (58)		можно вывести магнитную индукцию
поля, созданного:
а) бесконечно длинным прямым проводником с током:
	В =					0I	;		(59)
				2π		r
						0
б) отрезком проводника с током:
В =	0 I (cosα					1 −	cosα	2 ),	(60)
4π	r0

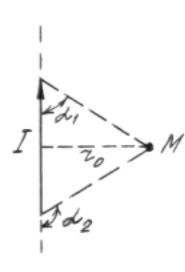
где r0 – кратчайшее расстояние от проводника до точки М , в которой

находится индукция магнитного поля; α 1 и α 2 – углы, определяющие границы проводника (рис. 9);

в) током в длинном соленоиде:

	В = 0nI,	(61)
где n – число витков провода на единице
длины соленоида.
Сила, действующая на прямолинейный
проводник длиной l с током I , помещенный
в магнитное поле индукцией B :
где α	F = I l B sinα ,	(62)
	- угол между проводником и вектором
!
B .
Магнитный момент контура с током
где S – площадь контура.	Рm = IS,	(63)

Магнитный поток Ф однородного магнитного поля через поверх-
ность площадью S :
Ф!=	B S cosα ,	(64)
где α - угол между вектором B	и нормалью к поверхности S .

		22
Потокосцепление соленоида
ψ	= NФ = LI,						(65)
где N – число витков соленоида;			L – его индуктивность.
Электродвижущая сила (основной закон электромагнитной ин-
дукции):			dФ
ε	= −				.		(66)

			dt
Электродвижущая сила самоиндукции:
ε с	= −	L		dI		.	(67)

				dt
Индуктивность соленоида:		0n2l S,
L =							(68)
где n – плотность витков (n =	N /l) ; l – длина соленоида; S – площадь

поперечного сечения соленоида. 4.2. Примеры решения задач

1. Два параллельных бесконечно длинных провода, по которым текут в противоположных направлениях токи I = 60 А, расположены на расстоянии d = 10 cм друг от друга. Определить магнитную индукцию в точке А, отстоящей от одного проводника на расстоянии r1 = 5 см и

от другого – на расстоянии

r2 =

12 см.

Дано:

Решение

I =

60 A

Значения индукции В1

и В2 магнитного поля прямого

d =

0,1м

тока находим по формуле (59):

r1 =

0,05 м

r2 = 0,12 м

2π r

2π

В - ?

Построив векторы

В1

и В2

как касательные к

силовым линиям

(рис. 10),

определяем модуль

результирующего вектора В по теореме косинусов:

В =

В2

+ В2

−

2В В сos α .

Сos α

вычислим из ∆ АДС:

Рис. 11

		r2	+	r2	− d 2
Сos α	=	1		2
Сos α	=			2r1r2
				2r1r2

Подстановка численных данных дает cosα Формула для B приобретает вид

= 0,576.

			µ 0 I		1	1		2
		В =	2π		r12 + r22		−	r1r2 cosα ,
B =	4π 10− 7 60	1 104		+	1 104	−	2 0,576 104		= 286 10− 3	Тл.
	2π		25		144			5 12

Ответ: В = 286 мТл.

2. Определить магнитную индукцию В

поля, создаваемого отрез-

ком бесконечно длинного прямого провода,

в точке М,

равноудален-

ной от концов провода и находящейся на расстоянии r0 =

20 см от про-

вода (рис. 9). Сила тока в проводе I = 30 A, длина отрезка

l = 60 см.

Дано:

Решение

I = 30 A

Воспользуемся формулой (60):

r0 = 0,2 м

В =

(cosα 1 −

cosα 2 ).

l = 0,6 м

4π

В - ?

При симметричном расположении точки М относительно отрезка

провода cos α

2 = − cos α

1. Следовательно:

В =

cosα 1.

Из рис. 9

видно, что

2π

l / 2

сosα 1 =

l 2 / 4

4r 2

+ l 2

В =

2π r0

4r02 + l 2

B =

4π 10− 7 30

0,6

(0,6)2

2,49 10− 5

Тл.

2π 0,2

4(0,2)2 +

Ответ: В = 2,49 10− 5 Тл = 24,9 мкТл.

3. По соленоиду течет ток I = 2 А. Магнитный поток Ф, пронизывающий поперечное сечение соленоида, равен 4 мкВб. Определить индуктивность L соленоида, если он имеет 800 витков.

Дано:					Решение
I = 2 A		По формуле (65) для потокосцепления находим
Ф = 4 мкВб				L		ψ			ФN
N = 800					=			=			,
N = 800					=		I	=	I		,
L = ?			4 10− 6 800
		L =	4 10− 6 800	=	1,6 10− 3					Гн.
		L =		=	1,6 10− 3					Гн.
	2
Ответ: L = 1,6 мГн.
5. Волновая оптика (задачи 41 – 50)
5.1.	Основные формулы
Оптическая разность хода двух лучей:
			∆ Х = S2n2 −			S1n1,					(69)

где S1 и S2 – геометрическая длина пути первого и второго лучей; n1 и n2 – показатели преломления сред, в которых эти лучи распространяются.

Условие интерференционного максимума интенсивности света:

∆ Х = ± Кλ , (70)

где К = 0, 1, 2… - порядок максимума; λ - длина волны световых лучей.

Условие интерференционного минимума интенсивности света:

∆ Х = ± (2К + 1)	λ .	(71)
	2

Оптическая разность хода лучей в тонких пленках в отраженном свете:

∆ Х =	2d	n2 − sin2 i +	λ ,	(72)
где d – толщина пленки;			2
где d – толщина пленки;	n – ее показатель преломления;			i – угол па-
дения лучей на пленку.
Условие максимума интенсивности света при дифракции на щели:
аsinϕ		= ± (2K + 1) λ	,	(73)
		2

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

Соседние файлы в папке Методички