
- •Кинетика и термодинамика ферментативных реакций
- •Специальность 020208.65 - Биохимия
- •Составитель: н.М.Титова
- •ВвЕдение
- •Раздел 1. Уравнение Михаэлиса-Ментен
- •Характеристика кинетических констант
- •Методы определения Км и Vmax
- •Задачи к разделу 1
- •Раздел 2. Ингибиторы ферментов
- •2.1. Конкурентное ингибирование
- •2.2. Неконкурентное ингибирование
- •2.3. Бесконкурентное ингибирование
- •2.4. Смешанный тип ингибирования
- •2.5. Методы определения константы ингибирования
- •2.6. Субстратное ингибирование
- •2.7. Задачи к разделу 2.
- •Раздел 3. Ферменты, не подчиняющиеся кинетике Михаэлиса-Ментен
- •3.1 Методы определения коэффициента Хилла
- •3.2. Определение коэффициента крутизны Кошланда
- •3.3. Задачи к разделу 3.
- •Раздел 4. Задачи к коллоквиумам и тестам
- •Оглавление
- •660041, Г. Красноярск, пр. Свободный, 79
- •660041, Г. Красноярск, пр. Свободный, 82а
Министерство образования и науки Российской Федерации
Сибирский федеральный университет
Кинетика и термодинамика ферментативных реакций
Учебно-методическое пособие
к практическим занятиям
Специальность 020208.65 - Биохимия
Красноярск
СФУ
2012
УДК 577.15(07)
ББК 28.072.534
Составитель: н.М.Титова
Кинетика и термодинамика ферментативных реакций: Сборник задач к практическим занятиям /[Текст] / сост. Н.М. Титова. – Красноярск: Сиб. федер. ун-т, 2012. – 64 с.
Сборник задач по курсу «Кинетика и термодинамика ферментативных реакций» составлен в соответствии с программой курса и является учебно-методическим руководством по решению задач по кинетическим свойствам ферментов.
В учебном пособии представлены четко структурированные задачи по основному разделу курса «Кинетика ферментативных реакций» разной степени сложности. Предназначено для студентов биологических и медико-биологических специальностей университетов.
УДК 577.15(07)
ББК 28.072.534
© Сибирский
федеральный
университет, 2012
ВвЕдение
В ферментативной кинетике концепция стационарности применима к концентрациям связанных с ферментом интермедиатов. Когда фермент смешивается с избытком субстрата наблюдается начальный период, известный как предстационарное состояние, в течение которого концентрации этих интермедиатов достигают стационарного уровня. По достижении интермедиатами стационарных концентраций скорость реакции относительно медленно изменяется со временем и именно в данный период традиционно измеряют скорости энзиматических реакций.
Стационарное состояние является аппроксимацией, поскольку субстрат постепенно превращается в ходе эксперимента. Но, принимая во внимание, что измерения осуществляются за короткий промежуток времени, когда концентрация субстрата изменяется незначительно, стационарное состояние является хорошей аппроксимацией. Хотя изучение предстационарной кинетики позволяет анализировать механизмы ферментативного катализа, стационарная кинетика более важна для измерения каталитической активности фермента при стационарных состояниях в клетке.
Раздел 1. Уравнение Михаэлиса-Ментен
Впервые А. Браун (Brown A.J.) и затем В.Анри (Henri V.) в начале ХХ века высказали предположение о том, что в основе ферментативной реакции лежит обратимое взаимодействис субстрата с ферментом с образованием комплекса, который далее распадается с образованием продуктов реакции и регенерацией исходного фермента. Эта гипотеза была далее развита в работах Михаэлиса (L. Michaelis) и Ментен (M.L. Menten) (1913 г.) и позднее – Бригсом (G.E. Briggs) и Холденом (J.B.S. Haldane) (1925 г.).
Кинетическую схему простейшей односторонней ферментативной реакции превращения одного субстрата в продукт можно представить следующим образом:
 (1.1)
(1.1)
Ферментативная реакция протекает в два этапа. На первом этапе фермент и субстрат образуют фермент-субстратный комплекс ES. Этот этап является быстрым и обратимым, он не сопровождается какими-либо химическими изменениями субстрата. Константы скорости реакции образования фермент-субстратного комплекса и обратного его распада равны соответственно k+1 и k-1. В образовании фермент-субстратного комплекса (ФСК, комплекс Михаэлиса) принимают участие нековалентные взаимодействия.
Каталитический процесс осуществляется на втором этапе реакции с константой первого порядка k+2 (kcat, число оборотов фермента). Комплекс Михаэлиса распадается с образованием конечного продукта реакции Р и регенерацией исходного фермента. Распад фермент-субстратного комплекса может происходить по-разному: в данной кинетической схеме он распадается в одну стадию, но в других случаях этих стадий может быть несколько.
Исходя из уравнения (1), можно расписать уравнения для скоростей отдельных стадий реакции.
Скорость образования фермент-субстратного комплекса:
![]() .
.
Скорость обратной реакции (диссоциации комплекса на исходные вещества):
![]() .
.
Скорость распада комплекса ES с образованием продуктов реакции и регенерацией фермента:
![]() .
.
Стационарное течение процесса возможно тогда, когда концентрация субстрата существенно превосходит концентрацию фермента ([S]>> [E]). В этом случае распад комплекса ES по реакциям (+2) и (-1) уравновешивается его образованием по реакции (+1). Поэтому для условия стационарности можно записать:
![]()
или
![]() .
.
Обозначив общую концентрацию фермента через [E]0, при условии, что [E]0 = [E] + [ES], преобразуем предыдущее уравнение
![]() .
.
Откуда концентрация фермент-субстратного комплекса будет равна
![]() .
.
Обозначив
![]() ,
,
получим
![]() .
.
Скорость ферментативной реакции, измеряемая согласно схеме (1) по образованию продукта реакции Р из комплекса ES, может быть выражена следующим образом
![]() .
.
Подставляя в это выражение найденное значение [ES], получаем
(1.2)![]()
Данное уравнение отражает зависимость скорости ферментативной реакции от концентрации фермента и субстрата. Константа Км носит название константы Михаэлиса и имеет размерность концентрации субстрата. Уравнение (2) свидетельствует, что зависимость скорости ферментативной реакции от концентрации субстрата при [E]0=const является гиперболической функцией (рис. 1.1).
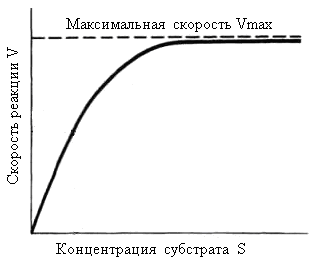
Рис.1.1. Зависимость скорости ферментативной реакции от концентрации субстрата
Кривая представляет собой равнобочную гиперболу. При достаточно малых концентрациях субстрата, когда [S] << Км, можно принять, что Км + [S] ≈ Км и тогда
V = k+2[E]0, [S]/ Км,
поэтому реакция имеет первый порядок по отношению к субстрату и является линейной функцией концентрации субстрата.
Когда [S] = Км, скорость реакции является полумаксимальной, т.е. v= 1/2 Vmax. В области высоких значений концентрации субстрата, когда [S] >> Км, можно принять, что Км + [S] ≈ [S], и тогда
v ≈ k+2[E]0 = Vmax,
а реакция имеет нулевой порядок по отношению к субстрату. Следовательно, при достижении определенной концентрации субстрата скорость ферментативной реакции достигает максимального значения Vmax и при дальнейшем увеличении концентрации субстрата не изменяется.
Смысл такого рода зависимости очевиден: скорость ферментативной реакции определяется в целом концентрацией фермент-субстратного комплекса и при малых концентрациях субстрата концентрация комплекса Михаэлиса пропорциональна [S], тогда как при избытке субстрата фактически весь фермент находится в форме ES. Дальнейшее повышение концентрации субстрата не приводит к увеличению [ES].
С учетом приведенного выше выражения, окончательное уравнение зависимости скорости ферментативной реакции от концентрации фермента и субстрата приобретает вид
![]() .
(1.3)
.
(1.3)
Уравнение (3) является фундаментальным уравнением ферментативной кинетики и обычно называется уравнением Михаэлиса-Ментен.
Скорость реакции приближается к максимальной достаточно медленно, и даже при [S]= 10Км, величина скорости достигает только 0,91 Vmax. В связи с этим значение максимальной скорости очень часто трудно измеримо и его приходится рассчитывать из скоростей, наблюдаемых при концентрациях субстрата ниже насыщающих.
