
Добавил:
fench
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:Курнаев Введение в пучковую електронику 2008
.pdf

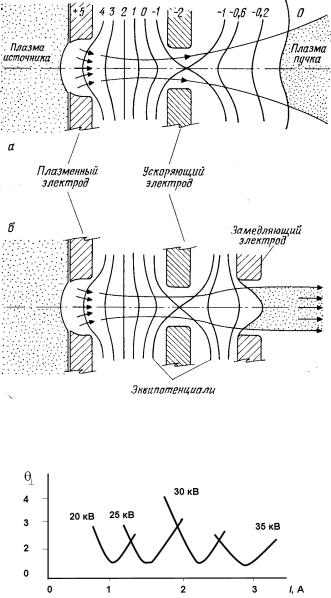
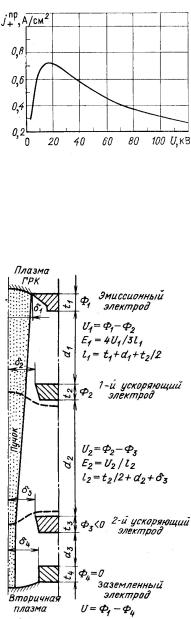
Рис. 3.87. Траектории ионов и эквипотенциали в ускоряющейзамедляющей ионно-оптической системе ионного источника с потенциалом относительно земли 5 кВ без специального замедляющего электрода (а) и с ним (б)
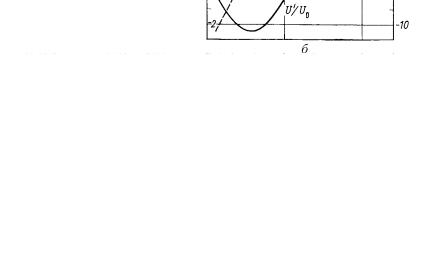
Рис. 3.88. Расходимость пучка ионов водорода, извлекаемого из плазменного источника ионов от тока разряда при разном ускоряющем потенциале при постоянном значении ускоряющего промежутка 4 мм
417
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
