Курнаев Введение в пучковую електронику 2008
.pdf
|
|
1 ∂B |
|
||
rot E = − |
|
|
|
; |
|
c |
|
∂t |
|||
|
|
|
|
||
|
|
|
|
|
|
div B = 0; |
|
|
|
||
|
4π |
|
|
|
|
rot B = |
j, |
|
|||
|
|
||||
|
c |
|
|
|
|
|
|
|
|
|
|
и закон Ома: j |
= σE |
эф |
= σ E + |
1 |
V × B . |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
К последнему уравнению системы применим операцию rot: |
||||||||||||||||||||
|
|
|
|
|
|
|
|
rot rot B = rot |
4π |
j ; |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|||
|
|
|
|
|
[a ×[b ×c]] = b (ac) −c (ab) ; |
|
||||||||||||||
|
×[ ×B] = ( B) − 2B = grad div B − 2 B = |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4π |
|
|
|
|
|
1 |
|
|
|
|
|
|||
|
|
|
|
= |
|
|
σ rot E |
+ rot |
|
|
V ×B |
|
; |
|||||||
|
|
|
|
|
c |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
1 ∂B |
c |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
=− |
|
∂t |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
∂B |
c |
|
|
c2 |
|
|
||||||||
|
|
|
|
|
|
= rot V |
×B + |
|
B . |
|
||||||||||
|
|
|
|
|
|
∂t |
|
4πσ |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Если плазма покоится, то V = 0 . |
|
|
|
|
|
|
|
|||||||||||||
∂B |
= |
c2 |
|
B – уравнение диффузии магнитного поля. |
||||||||||||||||
∂t |
4πσ |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
При |
σ = ∞ |
|
∂B = rot V |
× B – уравнение |
«вмороженности» |
|||||||||||||||
|
|
|
|
∂t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
магнитного поля. Уравнение диффузии магнитного поля имеет вид:
|
|
|
∂B |
|
|
|
|
|
|
∂2B |
+ |
∂2B |
+ |
∂2B |
; |
||||
|
|
|
∂t |
|
= Dмаг |
∂x2 |
|
∂y2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∂z2 |
|
|||||
|
|
|
|
|
|
|
|
|
c2 |
|
= D |
|
|
= δ2S ; |
|
(3.55) |
|||
|
|
|
|
|
|
|
|
4πσ |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
маг |
τS |
|
|
|
||||||
δ |
S |
= |
D |
τ |
S |
= |
|
c2 |
τ |
S |
|
– глубина скин-слоя. |
|||||||
|
4πσ |
|
|||||||||||||||||
|
|
маг |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
402 |
|
|
|
|||

V = 0 1c j × B = p – это условие равновесия плазмы, из которого
следует, что вектора j и B лежат на поверхности p = const , т.е. магнитные поверхности в плазме являются изобарическими. Если
магнитное поле однородно, то |
1 |
j × B |
|
= − |
|
Bz2 |
, т.е. газокинети- |
|
z |
8π |
|||||
|
c |
|
|
||||
B2
ческое давление уравнивается магнитным: p = − 8πz . Или
|
|
|
|
|
|
|
B2 |
|
B2 |
B2 |
||
можно записать: p + |
|
z |
= 0 p + |
|
= 0 p + |
z |
= const . |
|||||
8π |
|
|
||||||||||
|
|
|
|
|
|
|
8π |
8π |
||||
Если учесть, |
что вне плазмы Bz = B0 , |
то можно написать соот- |
||||||||||
|
B2 |
B2 |
|
|
|
|
|
|
|
|||
ношение: p + |
|
z |
= |
0 |
, т.е. магнитное поле в плазме ослабляется, |
|||||||
|
|
|
||||||||||
|
8π |
8π |
|
|
|
|
|
|
|
|||
плазма выталкивает магнитное поле как диэлектрик. Таким образом, магнитное поле в плазме зависит от давления плазмы и меня-
B2
ется так, чтобы оставалась постоянной величина p + 8πz = const .
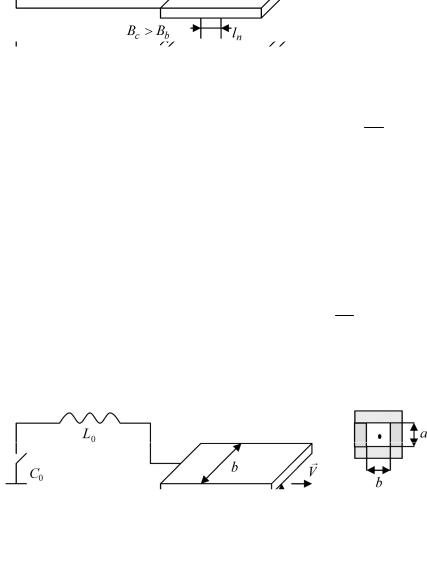
3.8.4.Рельсотрон
Водномерном случае плазменный ускоритель имеет вид рельсотрона (рис. 3.77).
Рис. 3.77. Рельсотрон
405