
Кулик Введение в теорию квантовых вычислений Книга 2 2008
.pdf
тогда
|
|
|
|
|
|
|
|
|
v = M3 ×{H X } = |
|
|
|
|
|
|
|
|
||||||||
|
|
|
1 0 0 0 |
|
|
|
|
|
0 1 0 1 |
|
|
|
|
|
|
0 1 0 1 |
|
||||||||
|
|
|
0 1 0 0 |
|
1 |
|
1 0 1 0 |
|
|
1 |
|
1 0 1 0 |
|
|
|||||||||||
|
= |
|
|
|
× |
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
, |
||
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|||||||||||||
|
|
|
0 0 0 1 |
|
|
|
0 1 0 −1 |
|
|
|
|
|
1 0 −1 0 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 0 1 0 |
|
|
|
|
|
1 0 −1 0 |
|
|
|
|
|
|
0 1 0 −1 |
|
||||||||
|
|
|
|
|
|
|
|
|
y = {X I }×v = |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
0 0 1 0 |
|
|
|
|
0 1 0 1 |
|
|
|
|
|
1 0 −1 0 |
|
|
|
|
||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||
|
= 0 0 0 1 |
× |
|
1 0 1 0 |
= |
0 1 0 |
−1 |
, |
|
||||||||||||||||
|
|
2 |
|
|
|
2 |
|
||||||||||||||||||
|
|
1 0 0 0 |
|
|
|
1 0 −1 0 |
|
|
|
0 1 0 1 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 1 0 0 |
|
|
|
|
0 1 0 −1 |
|
|
|
|
1 0 1 0 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
z = M3 × y = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 0 0 0 |
|
|
|
|
1 0 −1 0 |
|
|
|
|
|
1 0 −1 0 |
|
|
|
|
||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||
|
= 0 1 0 0 |
× |
|
0 1 0 −1 = |
0 1 0 |
−1 |
, |
|
|||||||||||||||||
|
|
2 |
|
|
|
2 |
|
||||||||||||||||||
|
|
0 0 0 1 |
|
|
|
0 1 0 1 |
|
|
|
1 0 1 0 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 0 1 0 |
|
|
|
|
1 0 1 0 |
|
|
|
|
|
0 1 0 1 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
M00 = {H I }× z = |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
1 0 |
1 0 |
|
|
|
|
1 0 −1 0 |
1 0 |
0 0 |
|
|||||||||||||
|
|
1 |
|
0 1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
0 0 |
|
|
||||||
= |
0 1 |
|
× |
|
0 1 0 |
−1 = |
0 1 |
|
, |
||||||||||||||||
2 |
|
|
|
|
2 |
|
|
||||||||||||||||||
|
1 0 −1 0 |
|
|
|
|
1 0 1 0 |
0 0 −1 0 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
0 1 |
0 −1 |
|
|
|
|
0 1 0 1 |
0 0 |
0 −1 |
|
|||||||||||||
т.е. получилась не совсем единичная матрица (так как один и тот же результат можно получить разными матрицами).
12). На этом закончим рассмотрение данного примера ▄
491

Прежде чем рассмотреть очередное правило для квантовой схемотехники, вернемся вновь к унитарной матрице гейта, реализующего некоторое унитарное преобразование.
В унитарных матрицах, которые мы рассматриваем, строки и столбцы нумеруются слева направо и сверху вниз, а сама нумерация представляется как
00…0, 00…1, …, 11…1,
причем самый нижний провод на квантовой схеме соответствует именно самому младшему биту.
На рис. 5.22, 5.23 представлены следующие матрицы:
|
|
|
|
a00 |
a01 |
a02 |
a03 |
|
a |
a |
|
, |
a |
a |
a |
a |
|
00 |
01 |
|
10 |
11 |
12 |
13 |
. |
|
a10 |
a11 |
|
|
a20 |
a21 |
a22 |
a23 |
|
|
|
|
|
|
a |
a |
a |
|
|
|
|
|
a |
|
|||
|
|
|
|
30 |
31 |
32 |
33 |
|
На рис. 5.22 представлена в общем виде унитарная матрица для однокубитового гейта, а на рис. 5.23 — для двухкубитового гейта.
Состояния | 0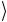 , | 1
, | 1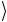 (для однокубитовых схем) или | 00
(для однокубитовых схем) или | 00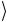 , | 01
, | 01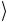 ,
,
| 10 , | 11
, | 11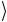 (для двухкубитовых схем) являются базисными состоя-
(для двухкубитовых схем) являются базисными состоя-
ниями и к тому же они, как правило, являются и вычислительным базисом. На рис. 5.22, 5.23 столбцы соответствуют базисным векторам на выходе гейта. Например, если на вход однокубитового
гейта поступил вектор | ψ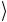 , который есть базисный вектор | 1
, который есть базисный вектор | 1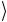 ,
,
т.е. | ψ =| 1
=| 1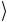 (рис. 5.22), то на выходе этого гейта будет выходной
(рис. 5.22), то на выходе этого гейта будет выходной
вектор | ψ |
′ |
из базисных векторов с амплитудами в соответствую- |
|
|
|||
|
|
′ |
= a01 | 0 + a11 | 1 . Аналогичное справедливо |
щем столбце, т.е. | ψ |
|||
и для двухкубитового гейта. Например, если на вход двухкубито-
вого гейта поступил базисный вектор | ψ =| 01 |
(рис. 5.23), то на |
|
|
′ |
из базисных век- |
выходе этого гейта будет выходной вектор | ψ |
||
торов с амплитудами в соответствующем столбце, т.е. |
||
′ |
= a01 | 00 + a11 | 01 + a21 | 10 + a31 |
| 11 . |
| ψ |
||
|
492 |
|

Из квантовой механики, из работы П. Шора [12, с. 211], из содержания главы 2 и данного раздела следует, что:
•тождественное преобразование с единичной унитарной матрицей I{n} не изменяет вектора | ψi  состояния i–го кубита или квантового регистра | Rg
состояния i–го кубита или квантового регистра | Rg ;
;
•если применяется гейт (с унитарной матрицей M) к двум кубитам большого вектора состояния квантового
регистра | Rg (предполагается, что квантовая схема состоит более чем из двух кубитов), то для каждого базисного вектора следует применять преобразование этого гейта, изменяющее состояние только этих двух кубитов согласно матрице M и не затрагивающее состояния других кубитов квантового регистра (это полностью соответствует умножению полного вектора состояния | Rg
(предполагается, что квантовая схема состоит более чем из двух кубитов), то для каждого базисного вектора следует применять преобразование этого гейта, изменяющее состояние только этих двух кубитов согласно матрице M и не затрагивающее состояния других кубитов квантового регистра (это полностью соответствует умножению полного вектора состояния | Rg , на тензорное произведение матрицы M
, на тензорное произведение матрицы M
этого гейта, действующего на два кубита, и единичных матриц I оставшихся кубитов).
Для многокубитовых схем (т.е. квантовых схем с числом кубитов больше двух) сформулируем следующее важное правило.
Правило 5.8 Если в многокубитовой схеме (т.е. в квантовой схеме, в
которой число кубитов квантового регистра больше двух) применяется двухкубитовый гейт (с унитарной матрицей M) к состояниям двух кубитов (предполагается, что кван-
товый регистр находится в состоянии | Rg ), то для
), то для
каждого базисного вектора следует применять преобразование этого гейта, изменяющее состояние только этих двух кубитов согласно матрице M и не затрагивающее состояния других кубитов в этом базисном состоянии ▄
Данное правило позволяет относительно быстро вычислять новый вектор состояния квантового регистра.
Следующий сокращенный пример показывает, как можно применять это правило.
494
Пример 5.27 (три кубита и состояние квантового регистра [12]) Имеется некоторая трехкубитовая квантовая схема. Унитарная матрица M для двухкубитового гейта известна:
|
|
|
2 |
0 |
0 |
0 |
|
|
1 |
|
|
2 |
0 |
|
|
M = |
0 |
0 |
|||||
|
|
|
|
|
. |
||
2 |
0 |
0 |
1 |
||||
|
|
1 |
|||||
|
|
|
0 |
0 |
1 |
|
|
|
|
|
−1 |
||||
Известен также исходный вектор состояния квантового регистра
| Rg =|110
=|110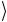 .
.
Требуется определить состояние квантового регистра | Rg′ на
на
выходе квантовой схемы, т.е. после применения этого двухкубитового гейта с унитарной матрицей M к первым двум кубитам.
Решение
1). Применим Правило 5.8, а для этого представим унитарную мат-
рицу M в следующем виде:
ВХОД
| 00 | 01
| 01 | 10
| 10 | 11
| 11
|
| 00 |
|
1 |
0 |
0 |
|
0 |
|
|
| 01 |
|
0 |
1 |
0 |
|
0 |
|
|
|
|
|
|||||
ВЫХОД |
| 10 |
|
0 |
0 |
1 |
|
1 |
|
|
|
|
||||||
|
2 |
|
2 |
|||||
|
|
|
|
|
|
|
||
|
| 11 |
|
0 |
0 |
1 |
− |
1 |
|
|
|
|
|
|
||||
|
2 |
|
||||||
|
|
|
|
|
|
2 |
||
495

2). На основании принципа суперпозиции произвольное состояние
| Rg |
рассматриваемого n-кубитового регистра при N=2n–1 |
имеет вид (n=3, N=7):
| Rg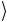 = a0 | 0...00 + a1 | 0...01 +...+ aN |1...11
= a0 | 0...00 + a1 | 0...01 +...+ aN |1...11
или
| Rg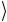 = a0 | 000 + a1 | 001 + a2 | 010 + a3 | 011 +
= a0 | 000 + a1 | 001 + a2 | 010 + a3 | 011 +
=a4 |100 + a5 |101 + a6 |110 + a7 |111 .
Вданном случае | Rg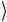 =|110
=|110 , т.е. имеем следующие ампли-
, т.е. имеем следующие ампли-
туды для входного состояния квантового регистра: a0=a1=a2=a3=a4=a5=a7=0, a6=1.
3). По условию задачи квантовая схема содержит 3 кубита, 1 двухкубитовый гейт, действующий на 2 первых кубита, а исходное
состояние квантового регистра есть | Rg =| 110
=| 110 . Тогда квантовая схема может быть представлена следующим образом:
. Тогда квантовая схема может быть представлена следующим образом:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ψ |
|
|
= | 11 |
|
|
|
|
|
|
|
M |
|
|
′ |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ψ12 |
|
|
||||||||
| Rg = |
| 110 |
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Rg′ |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
||||||||||||||||||
4). Так как | Rg |
=| 110 |
, |
то | ψ12 |
=| 11 , т.е. два первых кубита |
||||||||||||||||||||
находятся в состоянии | 11 , тогда согласно матрице M на вход |
||||||||||||||||||||||||
гейта поступает состояние | 11 , аеговыходобразуетсостояние |
||||||||||||||||||||||||
′ |
00 +0| 01 |
|
|
1 |
| 10 |
|
|
|
1 |
|
|
11 = |
1 |
| 10 − |
1 |
| 11 , |
||||||||
| ψ12 = 0| |
+ |
|
− |
|
| |
|
|
|||||||||||||||||
2 |
2 |
2 |
2 |
|||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
а значит |
| Rg |
= 2 |
|
| 100 − |
2 | 110 |
, |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
т.е. состояние 3-го кубита не меняется. 5). И тем самым задача решена▄
На этом закончим рассмотрение примеров.
496
5.7. Двухкубитовая схема алгоритма Дойча
«По сути, разработка многих квантовых алгоритмов сводится к хитроумному выбору функции и окончательного преобразования, позволяющих эффективно определять полезную глобальную информацию о функции — информацию, которую нельзя быстро получить на классическом компьютере.»
М. Нильсен, И. Чанг [1, с.58]
Рассмотрим очень важный пример одного из упрощенных и усовершенствованных вариантов [1, с.56-58] квантового алгоритма Д. Дойча для двух кубитов. Именно этот вариант легко может быть масштабирован на большее число кубитов (т.е. на многоразрядную логическую функцию f).
Алгоритм решает следующую задачу для булевой функции f, отображающей {0, 1} в себя.
Существуют только следующие 4 функции [7, с.53]:
постоянные
f1(0)= f1(1)=0; f2(0)= f2(1)=1;
сбалансированные
f3(0)=0, f3(1)=1; f4(0)=1, f4(1)=0.
Под сбалансированной функцией f понимается [1, с.58] такая функция, которая для одной половины всех возможных своих аргументов принимает значение 1 и принимает значение 0 для другой половины своих аргументов.
Имеется возможность вычислить значение функции только один раз. Случайно выбирается одна из 4 функций, но не известно, какая именно.
Ставится задача определить, что это за отобранная функция, т.е.
является ли она сбалансированной или постоянной.
Специально еще раз отметим, что в классическом случае для определения такого глобального свойства функции f требуется вычислить как значение f(1), так и значение f(0), что как, очевидно, потребует дважды вычислять значение этой функции.
497
Данная задача допускает следующую простую [13, с.131] интерпретацию с монетой.
В подлинной монете на одной стороне изображена решка, а на другой стороне — орел. В фальшивой монете на каждой стороне изображен орел. Для того чтобы определить подлинность монеты, необходимо посмотреть на монету дважды, т.е. один раз с одной стороны, а второй раз — с другой стороны. Таким образом, в классическом случае необходимо выполнить измерение дважды.
С помощью квантовых вычислений при решении этой задачи уже потребуется только однократное вычисление значения функции(т.е. всхемеиспользуетсятолько1 гейтUf, вычисляющий f).
ТеорияалгоритмаДойчаиегообобщения изложены в разделе 3.1 Квантовая схема, решающая эту задачу (см. [1, с.56-58; 13,с.132; 14, с.147]), представлена на рис. 5.24. На этой схеме показаны два однокубитовых регистра. Первый (верхний) кубит является регистром данных x для аргумента функции f(x), а второй (нижний) кубит является регистром значений y, т.е. результат (y f(x)) для
гейта Uf.
Квантовая схема для алгоритма Дойча на 2-х кубитах
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
| 0 |
|
|
|
|
|
|
|
H |
|
|
|
|
|
H |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
Uf |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
| 0 |
|
|
|
|
X |
|
|
H |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
T0 |
T1 |
|
|
|
|
|
|
|
|
|||||||||||
T2 |
|
T3 |
|
|
T4 |
|
T5 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Рис. 5.24 |
|
|
|
|
|
|
|||
Проведем подробное исследование (см. рис. 5.24) этой квантовой схемы.
1). В исходной квантовой схеме имеются два кубита (верхний кубит с номером 1, а нижний кубит с номером 2).
498

Первый кубит находится в базисном состоянии, т.е. | ψ1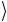 =| 0
=| 0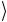 . Второй кубит также находится в базисном состоянии, т.е. | ψ2
. Второй кубит также находится в базисном состоянии, т.е. | ψ2 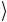 =| 0
=| 0 . На эти два кубита действует квантовая схема, содер-
. На эти два кубита действует квантовая схема, содер-
жащая три гейта H, гейт X и гейт Uf, а также измерительный элемент для измерения состояния первого кубита. В данной квантовой схеме каждый кубит является однокубитовым регистром, при этом оба этих кубита (т.е. регистра) представляют квантовую систему из двух кубитов (регистров), которую будем называть составным регистром, а состояние этого составного
регистра будем обозначать как | Rg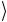 , причем входной вектор и
, причем входной вектор и
есть исходное состояние составного регистра, а выходной вектор есть конечное состояние составного регистра.
2). Будем далее предполагать, что входной вектор | Rg , промежу-
, промежу-
точные векторы состояний, выходной вектор | Rg′ и все мат-
и все мат-
рицы преобразования соответствуют одному и тому же вычислительному базису:
| 0 |
= |
1 |
, |
|1 |
= |
0 |
|
. |
|||||
|
|
0 |
|
|
|
1 |
3). Применим Правило 5.0б, результат Примера 5.15а и получим следующие векторы вычислительного базиса:
|
|
1 |
|
|
|
0 |
|
||
|
|
|
|
|
|
|
|
|
|
| 00 |
=| 0 | 0 |
= 0 |
|
, |
| 01 |
=| 0 |1 |
= 1 |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
||
|
|
0 |
|
|
|
0 |
|
||
|
|
0 |
|
|
|
0 |
|
||
|
|
|
|
|
|
|
|
|
|
|10 |
=|1 | 0 |
= 0 |
, |
|11 |
=|1 |1 |
= 0 . |
|||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
0 |
|
||
|
|
0 |
|
|
|
1 |
|
||
|
|
499 |
|
|
|
|
|
||
Таким образом, исходное состояние | Rg составного регистра
составного регистра
есть
1
| Rg =| ψ1
=| ψ1 | ψ2
| ψ2 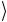 =| 0
=| 0 | 0
| 0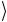 = | 00
= | 00 = 00 .
= 00 .
⎣0
4). Определим состояния кубитов | ψ1m  , | ψ2m
, | ψ2m  и состояние само-
и состояние само-
го составного регистра | Rgm 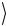 , где m=0, 1, 2, …, в различные
, где m=0, 1, 2, …, в различные
моменты времени Tm, отмеченные на схеме (рис. 5.24) как T0, T1, T2, T3, T4, T5. В моменты T0, T1, T2 эти состояния одинаковы
ине зависят от различных унитарных матриц гейта Uf.
Вмомент T0
| ψ10 |
= | 0 |
1 |
, |
| ψ20 |
= | 0 |
1 |
, |
= |
= |
||||||
|
|
0 |
|
|
|
0 |
|
1
| Rg0 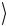 =| 00
=| 00 =| 0
=| 0 | 0
| 0 = 00 ,
= 00 ,
⎣0
т.е. кубиты и квантовый регистр находятся в чистом состоянии.
В момент T1 |
1 |
|
|
|
|
|
|
0 1 1 0 |
|
|||||||||
| ψ11 |
= | 0 |
, | ψ21 |
=X | 0 |
= |
=|1 , |
|||||||||||||
= |
|
|
|
× = |
||||||||||||||
|
|
0 |
|
|
|
|
|
|
1 0 0 1 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||
|
| Rg1 =| ψ 1 |
| ψ 1 |
= |
1 |
0 |
|
= |
1 |
|
= 1 |
, |
|||||||
|
|
1 |
2 |
|
|
|
|
|
|
|
|
0 |
0 |
|
||||
|
|
|
|
|
0 1 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
500 |
|
|
|
|
|
|
|
|
|
|
|
||


 |
| 
 |
|  |
|  |
| 