Борман Теория разделения изотопов 2007

(2.63) – (2.64). Если считать, что концентрации в начале секции заданы

то расчет секции сводится к решению уравнений (2.63) – (2.64), т.е. с начальными условиями (2.217) к обычной задаче Коши. Поскольку значения концентраций в каждой точке секции при известных концентрациях в потоке отбора ciP и

отвала ciW зависят от координаты s, отсчитываемой от нача-

ла секции, и потока секции L, задача сводится к поиску таких значений s и L, при которых функция (2.216) минимальна. На рис. 2.9 представлены зависимости относительных отноше-

приведенного потока ε0 L2P в каскаде постоянной ширины,

аппроксимирующего Q-каскад, для шестикомпонентной смеси изотопов криптона. Из рисунка видно, что в точке, соответствующей минимуму функции (2.216), относительные отношения концентрации малы и не превышают 3%.

Рис. 2.9. Зависимость относительных отклонений концентраций и функции невязки (216) от приведенного потока ε0L/ P [17]

241

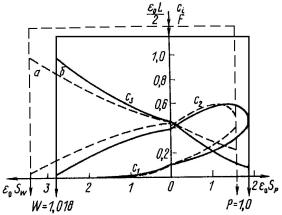
Таким образом, критерий (2.216) позволяет с определенной точностью рассчитать ПСК, в котором распределения концентраций компонентов близки к их распределению Q-каска- де. Однако этот ПСК в общем случае не оптимален по значению суммарного потока, являющегося одним из основных критериев оценки эффективности каскада, несмотря на то, что в критерии (2.216) использованы концентрации в соответствующих сечениях оптимального Q-каскада.

На рис. 2.10 представлены профили потока и распределения концентраций компонентов для двух прямоугольных каскадов, заменяющих Q-каскад, оптимальный в отношении суммарного потока. Оптимизация Q-каскада сводится к нахождению параметра М (формула (2.113)), соответствующего минимальному значению суммарного потока в каскаде. Параметры одного из каскадов выбраны в соответствии с минимумом функции (2.216), а второго – в результате оптимизации суммарного потока. Расчеты проведены для случая разделения трехкомпонентной модельной смеси с концентрациями в

Рис. 2.10. Распределение концентраций компонентов модельной трехкомпонентной смеси в каскаде прямоугольного профиля:

а – получено в результате аппроксимации Q-каскада, по критерию (2.216); б – оптимальное [18]

242

потоке питания c1F = 0, 2; c2F = 0,3; c3F = 0,5. Задача оп-

тимизации имеет следующую формулировку: определить параметры каскада с заданным отбором и концентрациями целевого компонента в потоке отбора из области допустимых значений (формулы (2.115) – (2.120)), соответствующих минимуму суммарного потока. Из зависимостей, приведенных на рис. 2.10, следует, что аппроксимация по критерию (2/216) не решает основной задачи – получить оптимальный ПСК на основе оптимального Q-каскада, так как суммарный поток, профиль и распределения концентраций в ПСК, полученных при аппроксимации, не совпадают с оптимальными. Так, в данном случае отклонение суммарного потока от его минимального значения составляет ~10%, а для смесей другого состава оно может быть и больше.

В работе [18] предложена методика аппроксимационного расчета ПСК и одновременной его оптимизации по какомулибо критерию. Методика основана на использовании целевой функции оптимизации, учитывающей как критерий оптимальности, так и сумму отклонений компонентов на стыке обогатительной (отборной) и обеднительной (отвальной) частей. В случае, когда в качестве критерия оптимальности выбран суммарный поток, целевая функция имеет вид

тания, полученные в результате интегрирования системы (2.63) – (2.64) по длине обогатительной (отборной) и обеднительной (отвальной) частей по направлению от концов каска-

да к точке подачи питания. ∑LПСК, ∑LQ – суммарные по-

токи аппроксимирующего ПСК и Q-каскада соответственно. Целевую аппроксимацию осуществляют в процессе оптимизационного поиска параметров каскада, при которых значе-

243

ние функции φ минимально. На каждом этапе оптимизации

проводят только интегрирование системы (2.63)–(2.64) с граничными условиями

где ciPQ , ciWQ – концентрации на концах аппроксимируемого

Q-каскада.

Первый член функции (2.218) определяет точность расчета ПСК, соответствующего оптимальному Q-каскаду и имеющего те же концентрации компонентов на концах. Второй член характеризует степень приближения ПСК к оптимальному по суммарному потоку Q-каскаду и является величиной обратной КПД* формы ηФ . Следует отметить, что

вместо КПД формы можно использовать отношение длин ПСК и Q-каскада или какой-либо другой критерий.

Для повышения точности расчета необходимо, чтобы члены функции (2.218) были одного порядка. С этой целью введены нормирующие коэффициенты K1 и K2 . Их

соотношения зависят от числа компонентов, состава исходной смеси, значения ключевого компонента в исходной смеси и значения его обогащения. Для определения диапазона изменения отношения K2 K1 в работе [18]

исследовали зависимости концентраций компонентов в потоках отбора и отвала и значения 1ηΦ для изотопных

смесей различного состава. В результате было определено, что для смесей различного состава с числом компонентов от 3 до 6 отношение K1 K2 изменяется в пределах от 10 до 30.

* Под КПД формы условно понимают в данном случае отно-

244

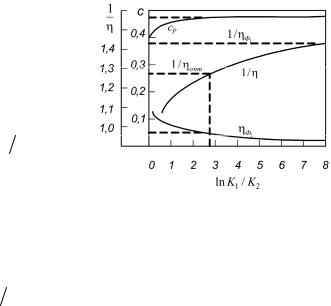
На рис. 2.11 приведены зависимости концентраций целевого компонента с2 рассмотренной трехкомпонентной смеси в

потоках отбора и отвала и значения обратного КПД формы от отношения коэффициентов K1K2 . Видно, что для

первым можно пренебречь, и результатом аппроксимации является ПСК, близкий к

рассчитанному по критерию (2.216) с КПД, равным ηΦ1 . При

малых K1K2 может нарушаться условие непрерывности

концентраций компонентов в точке подачи питания. В этом случае для уточнения расчета необходимо решить систему

где ciP, f , ciW, f – концентрации i-го компонента в точке подачи

питания, полученные из расчета от концов каскада, отборного и отвального соответственно.

245

Полученные в результате этого решения значения концентраций целевого компонента в потоках отбора и отвала могут существенно отличаться от заданных (см. рис. 2.9). Таким образом, схема расчета оптимального ПСК по данной методике имеет следующий вид: расчет и оптимизация Q-каскада; одновременный расчет и оптимизация ПСК, аппроксимирующего этот Q-каскад; уточнение концентрации целевого компонента в потоках отбора и отвала полученного каскада. Целесообразно оптимизацию Q-каскада и ПСК проводить по одному критерию. Изложенный подход может быть использован и при расчете каскадов, имеющих несколько потоков отбора и отвала.

2.3.5. Нестационарные процессы в каскаде [19–26] 2.3.5.1. Уравнение нестационарного переноса в каскаде

Математическую модель нестационарного разделительного процесса в приближении «слабого обогащения» (наличие большого числа разделительных ступеней, малость и независимость от текущих концентраций коэффициентов обогащения) по аналогии со случаем разделения бинарных смесей можно представить в виде следующей системы дифференциальных уравнений в частных производных [19–26]

перенос i-го компонента в направлении ступени с возрастающими номерами; t – время; s – координата, определяющая местоположение ступени в каскаде; H, T и L(s) – задержка раз-

246

деляемой смеси, перенос смеси и поток на входе s-ую ступень; εij – относительные коэффициенты обогащения пары

компонентов с номерами i и j. Если считать, что компоненты пронумерованы в порядке возрастания массовых чисел, и принять, что направление возрастания координаты s совпадает с направлением обогащения легких компонентов, то для молекулярно-кинетических методов разделения величина εij

где ε0 – коэффициент обогащения, приходящийся на еди-

ничную разность массовых чисел.

Обычно считают, что в системе уравнений (2.221) значения H, T и L(s) не зависят от времени. Если использовать но-

(221) приобретает вид, не зависящий от конкретного метода разделения

Для определенности рассмотрим прямоугольный каскад, имеющий в промежуточной точке поток питания F, а на концах каскада отводимые потоки – W (на «тяжелом» конце; условно – поток отвала) и P (на «легком» конце; условно – поток отбора). В этом случае перенос T определен как T = −W в отвальной секции каскада и T = P в отборной. Из условия сохранения переноса каждого компонента можно получить граничные условия для решения уравнений (2.224) в виде

247

ордината точки подачи потока питания; знаки +, - обозначают производные справа и слева от рассматриваемой точки.

Для решения полученной краевой задачи необходимо задание начального распределения концентраций всех компонентов по каскаду, которые в простейшем случае первоначального заполнения каскада однородной питающей смесью с

Таким образом, (m −1) уравнений вида (2.224) с краевыми условиями (2.225) – (2.227), начальным распределением

m

(2.228) и тождеством ∑c j (y,τ) ≡1 определяют полную сис-

j =1

тему для нахождения любой концентрации в каждой точке каскада в любой момент времени.

Приведенные выражения легко обобщить на случай каскадов любого профиля (с любым видом распределения потока L(s) ) и каскадов, имеющих несколько потоков питания и от-

бора. В случае расчетов каскадов, работа которых основана на использовании двухфазных (физико-химических) методов

248

разделения в краевых условиях, необходимо проводить учет накопления изотопов в емкостях, где происходит обращение фаз [19, 20, 24].

Моделирование переходных процессов связано с известными математическими трудностями даже применительно к случаю разделения бинарных смесей изотопов, когда система (2.224) приводится всего к одному уравнению в частных производных (см. раздел 1.12.1.). Если же число компонентов больше двух, то, по-видимому, единственно возможным является путь численного интегрирования, который в свою очередь предполагает разработку эффективных с точки зрения реализации на ЭВМ алгоритмов решения задачи.

Известные из литературы подходы к решению этой проблемы в основном сводятся к использованию сеточных ко- нечно-разностных и дифференциально-разностных моделей уравнений нестационарных процессов.

Существенным недостатком первых является то, что для краевых задач подобного типа достаточно устойчивыми оказываются неявные схемы, которые приводят к тому, что на каждом просчитанном временном слое приходится решать большие системы нелинейных алгебраических уравнений. Применение же традиционных явных методов, свободных от этого недостатка, ограничивается недопустимо малой величиной шага интегрирования по времени [19].

Второй подход обосновывается тем, что в настоящее время методы численного интегрирования обыкновенных дифференциальных уравнений развиты лучше, чем методы решения систем нелинейных алгебраических уравнений. Дифференци- ально-разностные модели («методы прямых») можно рассматривать как предельный случай сеточных моделей, когда одни из размеров сетки (шаг интегрирования по времени) стремится к нулю. В этом направлении можно выделить несколько работ. Например, в [20] краевая задача для каскадов с устройствами для обращения фаз путем асимптотических преобразований сведена к задаче Коши для системы обыкно-

249

венных дифференциальных уравнений. Это позволяет получить систему с хорошо обусловленными матрицами коэффициентов, что допускает использование для её решения простейших методов интегрирования, например, метода Эйлера. Однако апробация этой модели на молекулярно-кинетических методах разделения не дала положительных результатов. В работе [23] переход к системам обыкновенных дифференциальных уравнений осуществляется с помощью замены пространственных производных симметричными конечноразностными соотношениями. Решение системы производится методом типа Рунге–Кутта, который для своей устойчивости требует относительно малого шага интегрирования. В работах [24–25] разработан численный метод интегрирования системы (2.224) – (2.228), свободный от указанных недостатков. Ниже приводится краткое изложение сути этого метода.

Как известно [27], для решения линейных краевых задач параболического типа существует явный метод, который абсолютно устойчив, т.е. устойчив при любом законе стремления величин шагов интегрирования к нулю. Этот метод известен в литературе, как метод Дюфорта–Франкеля (E.DuFort, S.Frankel). Его идея состоит в том, что в симметричных ко- нечно-разностных соотношениях, аппроксимирующих дифференциальное уравнение в частных производных, проводится осреднение по двум соседним временным слоям центрального члена во второй пространственной производной. В работах [24–26] используется конечно-разностный сеточный метод, построенный по аналогии с методом Дюфорта– Франкеля. Для перехода к конечным разностям вся область интегрирования покрывается равномерной ортогональной сеткой: y = k∆ (k = 0, 1,KK) , τ = n∆τ (n =1, 2K) , где ∆ –

шаг интегрирования по пространственной переменной, ∆τ – шаг интегрирования по времени, n – номер временного слоя, k – номер пространственного узла на расчетной сетке.

250