Федеральное агентство по образованию

Гоу впо Кубанский государственный технологический университет (КубГту)

Кафедра автоматизации производственных процессов

Факультет Компьютерных технологий и автоматизированных систем

Лабораторный практикум по дисциплине

СИСТЕМЫ УПРАВЛЕНИЯ ХИМИКО-ТЕХНОЛОГИЧЕСКИМИ ПРОЦЕССАМИ

Методические указания к лабораторным работам для студентов всех форм обучения химико-технологических специальностей:

Краснодар

Издательство КубГТУ

2008

УДК 62-50.007(07)

Печатается по решению кафедры Автоматизации производственных процессов КубГТУ от 04.07 2008 г., протокол № 15.

Составитель: канд. техн. наук доцент В.И.Пугачев

СИСТЕМЫ УПРАВЛЕНИЯ ТЕХНОЛОГИЧЕСКИМИ ПРОЦЕССАМИ

Методические указания к лабораторным работам для студентов всех форм обучения технологических специальностей

Кубан.гос.технол.ун-т, сост.В.И.Пугачев.

Краснодар, 2008, 46 с.

Приведено описание к лабораторным работам по исследованию основных характеристик звеньев и системы автоматического управления, качеству их работы и особенностям цифровых систем управления, даны основные теоретические обоснования и требования к отчету.

Предназначены для студентов технологических специальностей, изучающих дисциплину: «Сиситемы управления технологическими процессами»

Ил. 10 Библиогр. 5 назв.

Рецензенты:

д-р техн. наук профессор зав. кафедрой МТМ и РП факультета пищевых биотехнологий и ресторанного бизнеса КубГТУ Г.И. Касьянов

канд. техн. наук, доц. каф. АПП Осокин В.В.

( Кубанский государственный технологический университет)

Лабораторная работа №1 Простейшие динамические звенья систем управления и их характеристики

1 Цель работы

Целью работы является ознакомление с основными понятиями, используемыми при анализе и синтезе систем управления, получение практических навыков использования основных характеристик звеньев и систем управления.

2 Общие сведения

2.1 Типовые входные сигналы

Исследование свойств звеньев или систем управления может быть проведено по реакции на одинаковые входные сигналы. В качестве ти­повых входных сигналов используются различные функции.

а) ступенчатая функция, аналитическое выражение которой можно записать так:

Функция называется единичной ступенчатой функцией. Реакция звена или системы управления на единичную ступенчатую функцию называется переходной функцией. Она может быть получена путем решения дифференциального уравнения при единичном ступенчатом входном воздействии. Если реакция звена или системы на ступенча­тое входное воздействие получена экспериментально, то она называется кривой разгона.

б) импульсная функция. Является производной ступенчатой функции и обозначается . Она представляет импульс бесконечно большой величины и бесконечно малой длительности интеграл от которой. Реально такой импульс иметь нельзя, одна­ко являясь математической идеализацией, он облегчает исследование САУ. Изображениеможно получить с помощью предельного перехода для изображения импульсного сигнала, когда его амплитуда стремится к бесконечности, а длительность к нулю.

.

Поскольку , а,

то - переходная функция звена или

системы, имеющей передаточную функцию .

Передаточная функция звена или системы есть отношение операторных изображений выходной и входной величин при нулевых начальных условиях.

Переходная и импульсная переходная функцияназываются временными характеристиками звена или системы.

.

в) гармоническая функция. Она может быть задана в веществен­ной или комплексной форме:

, или ,

где -угловая частота;- период колебаний.

Весьма удобной при исследовании CАУ оказывается комплексная форма задания гармонической функции:

.

При этом интерес представляет способность звена или системы воспроизводить входной сигнал на выходе, т.е. частное реше­ние неоднородного дифференциального уравнения которое также представляет гармоническую функцию, но с амплитудой и фазой, отличной от входного воздействия. Амплитуда и фаза выходной величины зависят от частоты и параметров системы. Поэтому исследование реакции звена или системы на гармоническое воздействие приводит к понятию частотных характеристик.

Пусть на САУ действует гармоническое воздействие. Тогда частное решение дифференциального уравнения будет также гармонической функцией, но отличающейся от входного воздействия по амплитуде и фазе.

;,

,

и т.д.

Если имеется дифференциальное уравнение

, (1)

то, заменив в нем значения входного и выходного сигналов и производных, получим

.

Отношение установившегося гармонического сигнала на выходе звена или системы к гармоническому входному сигналу называется амплитудно-фазовой характеристикой (АФХ)

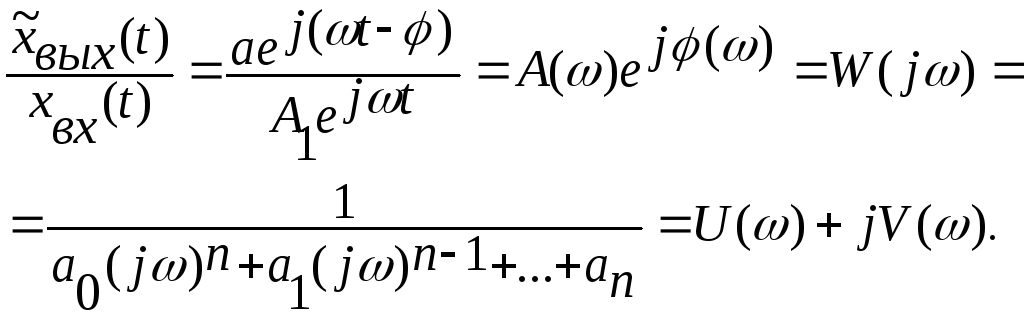(2)

где - вещественная часть амплитудно-фазовой характеристики;- мнимая часть амплитудно-фазовой характеристики.

В выражении (2) есть амплитудно-частотная характеристика;- фазочастотная характеристика.

Формально амплитудно-фазовая характеристика может бытьполучена путем замены в передаточной функциина. Действительно, дифференциальное уравнение (1) в операторной форме имеет вид:

,

откуда передаточная функция

,

амплитудно-фазовая характеристика

.

2.2 Типовые звенья САУ

По динамическим свойствам независимо от физической природы простейшие (неделимые) звенья подразделяются на усилительные (масштабные), апериодические, интегрирующие, дифференцирующие, ко­лебательные, звенья чистого запаздывания. На эти звенья можно разложить систему любой сложности, а также синтезировать из них желае­мую систему любой сложности.

Основными характеристиками звеньев являются: дифференциальное уравнение, передаточная и переходная функции, амплитудно-фазовая характеристика, логарифмические частотные характеристики (ЛАЧХ, ЛФЧХ).

Усилительные звенья

Особенностью усилительных звеньев является их практическая безынеционность, т.е. выходная величина в точности воспроизводит входную в измененном масштабе (усилители, потенциометры, редукто­ры, рычаги и т.д.):

, (3)

где - коэффициент усиления, который может быть больше и меньше единицы и иметь размерность, согласующую выходную и входную вели­чины.

В операторной форме (3) запишем так:

.

Передаточная функция усилительного звена:

.

Амплитудно-фазовая характеристика

не зависит от частоты.

На комплексной плоскости представляем точку на положительной вещественной оси, удаленную от начала координат за величину .

Если на вход звена подается ступенчатый единичный сигнал, то на выходе получается переходная функция в виде ступенчатого сигнала величины .

Апериодическое звено

Его называют инерционным звеном первого порядка, одноёмкостным статическим звеном. Дифференциальное уравнение его запишем так:

, (4)

где - постоянная времени, имеющая размерность времени,-коэффициент усиления.

В операторной форме (4) запишем так (при нулевых начальных условиях):

. (5)

Передаточная функция звена будет такой:

. (6)

Если , т.е., то

,

откуда .

Используя метод неопределенных коэффициентов, получаем:

.

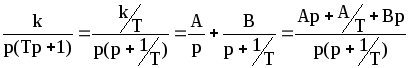Приравняв коэффициенты числителя при одинаковых степенях , получаем:

;.

Отсюда ;и

. (7)

Сделав в передаточной функции (6) замену , получим:

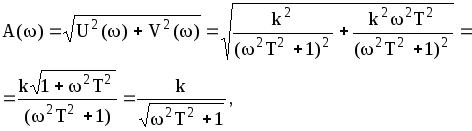. (8)

где - амплитудно-частотная характеристика.

Фазо-частотная характеристика .

(9)

АФХ апериодического звена представляет окружность с центром на вещественной оси на расстоянии и радиусом. Действительно,,

.

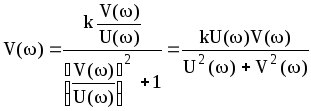Отсюда . Это выражение можно записать так:.

Оно представляет окружность радиусом с центром на вещественной положительной оси на расстоянииот начала координат (рисунок 1).

Рисунок 1 - АФХ апериодического звена

Интегрирующее звено

Выходная величина интегрирующего звена равна интегралу по вре

мени от входной, , или

. (10)

В операторной форме выражение (10) запишем так:

, передаточная Функция звена равна:

; . (11)

Решение уравнения (4.12) при нулевых начальных условиях и при единич­ном входном воздействии имеет вид:

, или , (12)

где - постоянная времени интегрирования, численно равна време­ни, через которое значение выходной величины станет равно входному воздействию (рисунок 4.3).

Амплитудно-Фазовая характеристика интегрирующего звена по­лучается из уравнения (11) заменой :

. (13)

Очевидно, что АФХ интегрирующего звена совпадает с мнимой осью комплексной плоскости, начинаясь в прии стремясь к нулю при.

Примерами интегрирующих звеньев могут служить гидравлический сервомотор, электрический двигатель постоянного тока, если выходной величиной является угол поворота, одноёмкостный объект без саморегулирования.

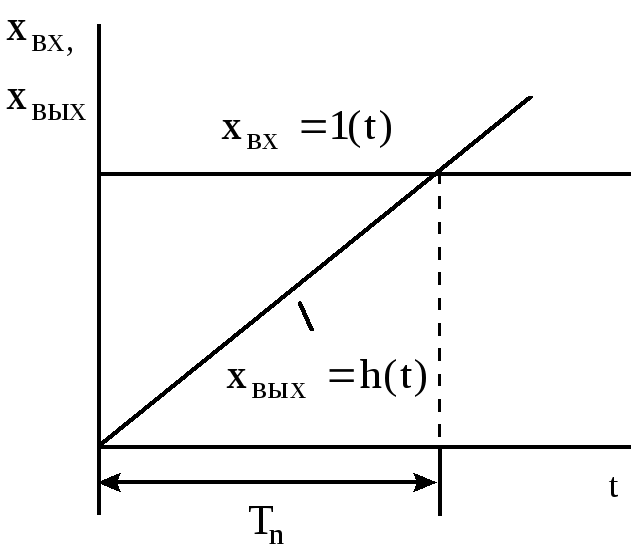
Рисунок 2 - Иллюстрация постоянной времени идеального интегрирующего звена

Дифференцирующее звено

Для идеального (физически не реализуемого) дифференцирующего звена выходная величина пропорциональна скорости изменения входной

, (14)

где - постоянная времени дифференцирования.

Если на вход такого звена подавать сигнал, изменяющийся с постоянной скоростью, то выходной сигнал будет постоянен. Время, за которое входной сигнал, изменяясь с постоянной скоростью от нуля до единицы, обеспечит выходной сигнал равный единице, называется постоянной времени дифференцирования идеального дифференцирующего звена.

Переходная функция дифференцирующего звена представляет бесконечно большой амплитуды и бесконечно малой длительности импульс, площадь которого равна .

,

где 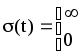при.

Передаточная и амплитудно-фазовая характеристики дифференцирующего звена получаются из выражения (4.16) и равны:

; . (15)

Легко видеть, что АФХ дифференцирующего звена совпадает с мнимой осью. Она начинается в начале координат при и устремляется в верхнюю полуплоскость при.

Колебательное звено

Статические и динамические свойства колебательного звена описываются дифференциальным уравнением второго порядка вида

, (16)

где ,- постоянные времени, имеющие размерность времени. В операторном виде уравнение (16) запишем так:

, (17)

откуда передаточная функция

. (18)

Для получения переходной функции необходимо решить уравнение (17) при единичном входном воздействии. При этом решение будет зависеть от вида свободной составляющей, определяемой корням характеристического уравнения

, (19)

где .

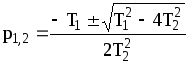Рассмотрим вид переходной функции для различных видов корней характеристического уравнения (19).

а) . В этом случае корнибудут вещественными отрицательными,,. Вынужденная составляющая может быть найдена исходя из нового установившегося состояния, когда

. (20)

Полное решение уравнения (17) имеет вид

. (21)

Постоянные интегрирования иопределяют по начальным условиям. При ступенчатом воздействии,равно нулю при. В противном случае, что невозможно, поскольку правая часть уравнения (4.19) конечна. Аналогичнопри, так как иначеравнялось бы бесконечности. Учитывая это обстоятельство, получим систему уравнений:

(22)

откуда ;.

Переходную функцию запишем так:

. (23)

б) .,

. (24)

Для нулевых начальных условий, обоснование которых дано выше, имеем:

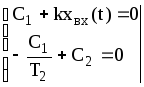(25)

отсюда ;.

. (26)

в) , где;,

. (27)

Постоянные интегрирования инайдем по нулевым начальным условиям,

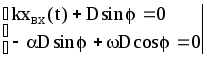, (28)

откуда ,

.

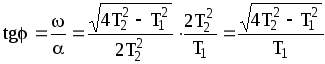. (29)

С учетом выражения (29) переходная функция принимает вид:

(30)

При условии инерционное звено второго порядка превращается в колебательное. Мнимая часть корней является круговой частотой колебаний,, где- период колебаний. Оценку переходного процесса в колебательном звене производят по относительной степени затухания:

;

.

Степень затухания тем больше, чем больше отношение , и равна единице при. Если, то, при этом, и переходная функция (4.33) принимает вид:

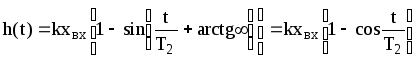. (31)

Амплитудно-фазовая характеристика колебательного звена получается из выражения (18) заменой :

(32)

. (33)

. (34)

При АФХ колебательного звена, начинаясь на положительной вещественной полуоси комплексной плоскости, проходит 4-й и 3-й квадранты и приближается к началу координат при изменении.

Если корни характеристического уравнения вещественные отрицательные, то передаточную функцию (18) можно записать так:

. (35)

Это эквивалентно включению последовательно двух апериодических звеньев, а звено называется апериодическим второго порядка.

Звено чистого запаздывания

Уравнение, связывающее выходную и входную величины:

. (36)

Передаточная функция звена

. (37)

Амплитудно-фазовая характеристик

. (38)

АФХ представляет на комплексной плоскости окружность единичного радиуса с центром в начале координат.

ЛАЧХ сливается с осью абсцисс, а ФЧХ есть линейная функция , проходящая через начало координат.

2.3 Основные законы регулирования

Будем считать, что на вход регулятора подается сигнал рассогласования между заданным и действительным значением регулируемой величины :

. (39)

Кроме того, рассмотрим законы регулирования идеальных регуляторов, т.е. таких, какими стремятся их сделать. Однако конст­руктивные особенности, условия физической реализуемости, наличие промежуточных неидеальных звеньев приводят к появлению дополни­тельных балластных звеньев типа апериодических, искажающих желаемые свойства регулятора.

В настоящее время промышленные регуляторы реализуют следующие основные законы регулирования: П - пропорциональный, И - интегральный, ПИ - пропорционально-интегральный ПД - пропорционально-дифференциальный, ПИД - пропорционально – интегрально - дифференциальный.

Для идеального регулятора, реализующего П - закон регулирования справедливо соотношение

, (40)

где - неравномерность регулятора - то изменение регулируе­мой величины, которое обеспечивает полный ход регулирующего органа.

Интегральный регулятор

Описывается уравнением

(41)

где - постоянная времени интегрирования, является настроеч­ным параметром регулятора. Характеристики его аналогичны характеристикам идеального интегрирующего звена.

Пропорционально-интегральный регулятор

Может быть реализован с независимыми параметрами настройки :

(42)

и с зависимыми:

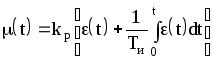. (43)

В случае (42) называется постоянной времени интегри­рования и есть время, через которое выходная величина за счет интегральной составляющей достигнет значения входного воздействия. Проинтегрировав (42), получим

.

При второе слагаемое равно, т.е. входной величине.

В случае (43) называется временем изодрома или временем удвоения. Проинтегрировав (43), получим

.

При второе слагаемое, получаемое за счет интегральной составляющей, достигает значения выходной величины, получаемой за счет пропорциональности составляющей, а на выходе регулятора результирующий сигнал удваивается.

Записав выражения (42) и (43) в операторной форме, легко получить передаточную функцию регулятора:

или из выражения (43):

(44)

В дальнейшем рассмотрим свойства ПИ-регулятора, имеющего передаточную функцию вида (44). АФХ регулятора:

(45)

где .

АФХ регулятора изображена на рисунке 3.

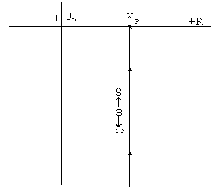
Рисунок 3 – Амплитудно-фазовая характеристика ПИ – регулятора

Пропорционально-дифференциальный регулятор

Связь выходной и входной величин определяется соотношением

(46)

где - постоянная времени дифференцирования.

Передаточная функция имеет вид

(47)

Амплитудно-фазовая характеристика

(48)

На комплексной плоскости представляет прямую, начинающуюся на положительной вещественной оси на расстояниии проходящую параллельно мнимой оси в первом квадранте.

Пропорционально -интегрально-дифференциальный регулятор

Имеет три параметра настройки: изменяемые в определенном диапазоне. Связь выходной величины регулятора с входной такая:

(49)

Записав (4.70) в операторной форме и взяв отношение выходной величины к входной при нулевых начальных условиях, получим передаточную функцию регулятора:

. (50)

Амплитудно-фазовая характеристика (АФХ):

.

(51)

ПИД - регулятор соединяет положительные свойства «ПИ» и «ПД»-регуляторов. Благодаря интегральной составляющей исключается статическая ошибка, а благодаря наличию производной в законе регулирования увеличивается коэффициент усиления регулятора на высоких частотах, что повышает его быстродействие.