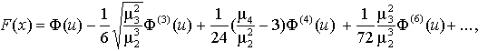Обработка эксперим данных Роганов
.pdf

|
|
|
|
|
|
|
|
|
|
|
Математическое ожидание m1, |
||
|
|
Тип и функция плотности |
дисперсия m2, |
||||||||||
|
|
асимметрия b1 = m3 / m23 / 2 , |
|||||||||||
|
|
|
|
распределения |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
эксцесс b2 = m4 |
/ m22 |
|
|
|
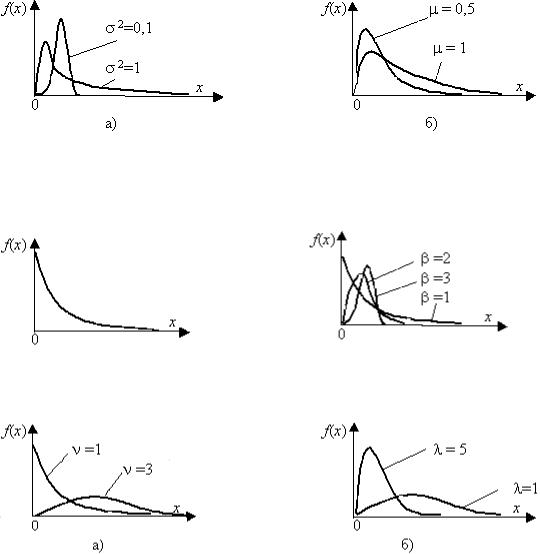
Нормальное |
|
|
|
m1 = μ1, m2 = σ2 = 2, |
|||||||
1 |
exp(− (x − μ1 )2 |
/(2σ 2 )), − ∞ < x < +∞ |
b1 = 0, b2 = 3 |
|
|||||||||
|
|
|
|||||||||||
σ 2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
Логарифмически нормальное |
m1 = exp(μ1 +0,5μ2 ), |
|
|||||||||||
1 |
|
|
|
|
(ln x − μ )2 |
|
,0, х ≤ 0 |
m2 = exp(2μ1 + μ2 )(exp(μ2 )−1), |
|||||
|
|
|
|
|
|
|
1 |
|
x > 0 |
|
|
|
|
σx 2π |
exp − |
|
2σ |
2 |
, |
b1 = (exp(μ2 )+ 2) exp(μ2 )−1, |
|||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
b2 = exp(4μ2 )+ 2exp(3μ2 )+3exp(2μ2 )−3 |
||
|
|
Экспоненциальное |
|
m1 = 1/λ m2 = 1/λ2 |
|||||||||
|
|
λexp(-λx), x≥ 0, 0, x < 0 |
b1 = 2, |
b2 = 9 |
|
||||||||
β |
x |
|
|
Вейбулла |
|
|
m1 =δg1, m2 |
=δ 2 (g2 − g12 ), |
|||||
β −1 |
|
x |
β |
|
x ≥ 0, 0, x < 0 |
|
|
3 |
|||||
|
δ |
|
|
exp − |
|
|
, |
b1 = (g3 −3g1g2 + 2g13 )/(g2 − g12 ) 2 , |
|||||
δ |
|
|
|
|
δ |
|
|
|
a = (g4 −4g1g3 +6g2 g12 −3g14 ), |
||||
|
|
|
|
|
δ > 0, β > 0 |
|
|||||||
|
|
|
|
|
|
a |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b2 = (g2 − g12 )2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
gi = Γ(1+i / β ) |
|
|
|
|
|
|
|
Гамма |
|
|
m =ν / λ, |
m =ν / λ2 |
, |
|||
|
λν |
|
xν −1 exp(−λx), |
|
|
|
1 |
2 |
|
||||
|
|
x ≥ 0, 0, x < 0 |
b1 = 2 / ν , |
b2 = 3(ν + 2)/ν |
|||||||||
Γ(ν ) |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
ν > 0, λ > 0 |
|
|
|
|
||||
Следует |
|
отметить, |
что |
гамма-распределение |
соответствует |
||||||||
распределению Эрланга, если λ – целое, и экспоненциальному |
|||||||||||||
распределению при ν = 1. |
|
|
|
|
|||||||||
|
|
После выбора подходящего вида распределения производится оценка |
|||||||||||
его параметров, используя методы максимального правдоподобия, моментов |
|||||||||||||
или квантилей. В целях упрощения решения задачи в табл. 8.2 приведены |
|||||||||||||
расчетные формулы для вычисления оценок параметров типовых |
|||||||||||||
распределений. |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 8.2 |
127

Тип |
|
Оценка параметров распределения |
|
||||||||||||||
распределения |
|
|
|
|
по выборочным данным |
|
|||||||||||
Нормальное |
|
|
|
|
n |
|
|
|
|
|
|
|
|
n |
|
(xi − μ)2 |
|
|
|
μ1 |
= |
1 ∑xi , |
μ2 |
=σ 2 |
|
= |
n |
1 |
∑ |
|
|||||
|
|
|
|
|
n i=1 |
|
|
|
|
|
−1 i=1 |
|
|
|
|||
Логарифмически |
|
μ1 = |
|
n |
μ2 |
|
|
|
|
|
1 |
n |
|
(ln xi − μ)2 |
|
||
|
1 ∑ln xi , |
=σ 2 |
|
= |
n |
∑ |
|
||||||||||
нормальное |
|
|
|
n i=1 |
|
|
|
|
|
−1 i=1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Экспоненциальное |
|
|
|
|
λ = |
1 |
|
1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
∑xi |
|
|
|
|||||
|
|
|
|
|
|
|
n i=1 |
|
|
|
|
|
|
||||
Вейбулла |
|
|
|
ln a ln xq −ln b ln xp |
|
|
|
ln a −ln b |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
β = |
|
|
, |
|
|
δ = exp |
ln a −ln b |
|
|
|
, |
ln xq −ln xp |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
0 < q < p <1, a = −ln(1− p), b = −ln(1−q) |
|
|||||||||||||||
|
|
|
xq, xp — выборочные квантили |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
Гамма |
|
(0,5001−0,1649q −0,0544q )−1, |
0 < q ≤ 0,577, |
||||||||||||||
|
|
||||||||||||||||
|
a = |
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
(8,899 +9,060q +0,9775q2 ) |
−1, 0,577 < q ≤17, |
||||||||||||||
|
|
|
|
(17,80 +11,97q + q |
2 |
)q |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
где q=ln(μ 1/6), β = μ1 /(1 + a), |
|
n |
|
|||||||||||||
|
μ1 = 1 ∑xi |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n i =1 |
|
Применительно к выбранному закону распределения производится проверка гипотезы о том, что имеющаяся выборка может принадлежать этому закону. Если гипотеза не отвергается, то можно считать, что задача аппроксимации решена. Если гипотеза отвергается, то возможны следующие действия: изменения значений оценок параметров распределения; выбор другого вида закона распределения; продолжение наблюдений и пополнение выборки. Конечно, такой подход не гарантирует нахождение "истинного" или даже подбора подходящего закона распределения. Преимущество применения типовых законов распределения состоит в их хорошей изученности и возможности получения состоятельных, несмещенных и относительно высоко эффективных оценок параметров. Однако
128