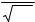Обработка эксперим данных Роганов

критериев, называемых критериями согласия, составляет одну из важных задач математической статистики.

Рассмотрим случай простой гипотезы H = (FX (x)= F (x)). Пусть

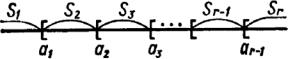
X1, X2 , ..., Xn – случайная выборка, т.е. наблюдаемые значения случайной величины Х, и пусть Fn* (x) эмпирическая функция распределения выборки.

Определим некоторую неотрицательную меру D отклонения

можно определить многими способами, в соответствии с которыми получаются различные критерии для проверки интересующей нас гипотезы. Например, можно положить

получим критерий Колмогорова, во втором случае (при k =1) – критерий ω2

Мизеса.

Величины X1, X2 , ..., Xn, образующие выборку, в случае справедливости выдвинутой гипотезы можно рассматривать как независимые одинаково распределенные случайные величины с функцией распределения

F(x). Но тогда величина D, как бы она ни была определена, является функцией от случайных величин и поэтому сама есть величина случайная.

111

осуществление события с вероятностью ε в единичном опыте. Считая известным распределение случайной величины D, можно найти такое число

означает, что событие с вероятностью ε произошло (т.е. произошло событие, которое считаем практически невозможным).

Таким образом, если D > Do, то предположение о справедливости выдвинутой гипотезы привело к выводу, что произошло практически невозможное событие, т.е. гипотеза опровергнута опытом. Если же вычисленная величина D(Fn* , F ) окажется меньше Do , то считают, что гипотеза не противоречит опытным данным и, возможно, может быть принята.

Отметим, что опровержение гипотезы при D > Do ни в коем случае не означает логического опровержения, равно как и подтверждение гипотезы в

возможностью можно пренебречь. Событие D < Do может осуществиться и в случае, если наша гипотеза неверна, поэтому ее необходимо проверить с помощью большого числа различных критериев, прежде чем считать ее подтвержденной опытными данными.

Выясним статистический смысл ε . Предположим, что производится последовательность серий однородных испытаний. Рассмотрим n серий, в которых гипотеза Н справедлива. Если mn – число тех из них, в которых эта

гипотеза отклонена, то mn →ε при n → ∞. n p

112

Число ε , выбор которого зависит от характера задачи, называют уровнем значимости критерия, а величину Do , определяемую из условия

P{D > D0 }= ε , – пределом значимости.

подлежащие оценке по выборке, так же рассматривают некоторую меру

D(Fn* , F ) отклонения эмпирической функции распределения

F(x,α1,α2 ...,αk ). Последняя в этом случае сама является величиной случайной, так как α1, α2 , ..., αk – функции наблюдаемых значений, и,

следовательно, случайные величины.

Критерий χ2 в случае простой гипотезы

При получении критерия для проверки гипотезы, состоящей в том, что функция распределения FX (x) случайной величины Х есть вполне определенная функция F(x), мы условились образовывать меру D

отклонения эмпирической функции распределения Fn* (x) выборки

X1, X2 , ..., Xn от предполагаемой (теоретической) функции распределения

F(x). Наиболее употребительной является мера, введенная Пирсоном,

приводящая к так называемому критерию χ2 Пирсона. Разобьем множество

113

чисел a1 < a2 <...< ar−1. При этом правый конец каждого интервала исключают из соответствующего множества, а левый – включают (рис. 3).

Величина χ2 случайная и нас интересует ее распределение,

вычисленное в предположении, что принятая гипотеза верна, т.е.

FX (x)= F(x).

Если распределение величины χ2 известно, то по заданному уровню значимости можно найти предел значимости для проверки принятой гипотезы. Не вычисляя распределение величины χ2 при каждом значении n,

укажем ее предельное (при n → ∞) распределение. Ответ на вопрос о

114

предельном распределении величины χ2 дает теорема Пирсона, которая приводится без доказательства.

Теорема Пирсона. Какова бы ни была функция распределения F(x)

случайной величины Х, при n → ∞ распределение величины χ2 стремится к

χ2 - распределению с (r −1) степенями свободы, т.е. при n → ∞

P(χ 2 < x)→ ∫x kr−1 (t)dt

0

в каждой точке х, где kr−1 (x) – плотность распределения χ2 с (r −1)

степенями свободы.

С помощью теоремы Пирсона введем критерий для проверки гипотезы. Зададим число ε > 0 такое, что событие с вероятностью ε (ε – уровень значимости) можно считать практически невозможным. По таблице для распределения χ2 с (r −1) степенями свободы найдем такое число χε2

(предел значимости), что

можно считать практически невозможным. Таким образом, если гипотеза верна, т.е. Fε (x)= F(x), то значения χ2 , превышающие предел значимости

χε2 , практически невозможны. Если для данной выборки окажется, что

χ2 > χε2, то гипотезу считают опровергнутой опытными данными; если же

χ2 ≤ χε2 , то опытные данные можно считать совместимыми с принятой

гипотезой, однако одного этого еще недостаточно для установления истинности гипотезы.

115

Применение теоремы Пирсона на практике дает достаточно хорошие результаты во всех случаях, когда величины npi ≥10, i = 1, 2, ..., r .

Критерий согласия Колмогорова

Рассмотрим случай, когда гипотетическая функция распределения полностью определена, т.е. задана функция F(x)= FX (x), которую предположим непрерывной. Мера D отклонения эмпирической функции распределения Fn* (x) выборки X1, X 2 , ..., X n от гипотетической функции распределения F(x), предложенная А. Н. Колмогоровым, определяется следующим образом:

Dn = D{Fn* , F}=sup Fn* (x)− F(x),

x

где sup – верхняя грань множества по всевозможным значениям х.

справедлива. Ответ на поставленный вопрос дает следующая теорема. Теорема Колмогорова. Если функция распределения F(x) непрерывна,

то при n →∞

Функция распределения К(х) табулирована ввиду ее важности для практики.

!!!!!!!!!!!!!!НЕТ ПАРАГРАФОВ 1-3!!!!!!!!!!

§ 4. Экспоненциальное распределение

Такие величины используются при моделировании на тренажерах "времени появления". Например, если в заданный интервал времени порывы ветра бывают в среднем один раз, то промежутки времени между двумя

116

последовательными порывами ветра имеют экспоненциальное распределение со средним значением μ . Это распределение записывается как:

F(x) =1− e−x / μ , x ≥ 0 .

Отсюда следует, что если X имеет экспоненциальное распределение со средним значением 1, то μ X подчиняется экспоненциальному распределению со средним μ . Поэтому достаточно рассмотреть случай при

μ =1. Из известных методов [Кнут] рассмотрим логарифмический метод и метод случайной минимизации.

X = −lnU

распределена экспоненциально со средним значением, равным единице (в программах, реализующих алгоритм следует избегать U = 0 ).

§ 5. Нормальное распределение

Считается, что нормальное распределение со средним значением, равным нулю, и стандартным отклонением, равным единице, возможно является важнейшим из неравномерных непрерывных распределений. Стандартная запись такого распределения:

Для его генерации существует несколько методов. Один из них получил название метода полярных координат.

117

В основе этого метода лежит использование двух независимых случайных чисел U1 и U 2 для получения двух независимых нормально распределенных величин X1 и X 2 [Кнут]. Предлагается следующий алгоритм

(рис. А2) генерирующий по два нормально распределенных числа. При необходимости увеличения количества требуемых величин необходимо повторять этот алгоритм снова и снова, получая каждый раз по паре требуемых чисел.

Существует метод доказательства точности предложенного алгоритма. Он связан с аналитической геометрией, что во многом послужило причиной

распределенным случайным величинам U1 и U 2 :

1.Получить два случайных числа U1 и U 2 , равномерно распределенных между 0 и 1.

2.Пересчитать интервал распределения, задав границы –1 +1 для

переменных V1 и V2 . Для этого вычислить V1 = 2U1 −1 и V2 = 2U 2 −1.

3.S =V12 +V22 .

4.If S ≥1 then шаг 1

else

6. Повторить шаги 1-5.

При S <1, точка плоскости с декартовыми координатами (V1 , V2 ) является

случайной точкой, равномерно расположенной внутри единичного круга

радиусом R .

118

Кроме того, Θ' равномерно распределена между 0 и 2π , а вероятность

Тогда вероятность того, что X1 ≤ x1 , а X 2 ≤ x2 , равна

Это доказывает, что X1 и X 2 независимы и нормально распределены.

Рассмотренный случай относится к нормальному распределению с нулевым средним значением и стандартным отклонением, равным единице.

119

§ 6. Другие виды числовых распределений

На практике, достаточно часто требуется не только нормальное распределение, но и другие виды распределений. Большинство из них были рассмотрены Джоном фон Нейманом, а затем улучшались по мере необходимости.

Существует множество алгоритмов формирования случайных и псевдослучайных последовательностей [Кнут]. Рассмотрим наиболее простые и часто используемые.

Самое общее распределение действительных случайных величин описывается в терминах "функции распределения" F(x) . То есть необходимо,

чтобы случайная величина X принимала значение, меньшее или равное x с вероятностью F(x) :

F(x) = вероятность (X ≤ x) .

Эта функция всегда монотонно увеличивается от нуля до единицы:

F(x1 ) ≤ F(x2 ) , если x1 ≤ x2 ;

120