3.1 Поступательное движение твердого тела

Это такое движение, при котором любая прямая, про­веденная в теле, перемещается параллельно самой себе. Теорема: при поступательном движении все точки тела перемещаются по одинаковым траек­ториям и имеют в каждый момент равные (по величине и направлению) скорости и ускорения.

И з AOB:

. (*)

Так как , то траектории точек A и B при наложении совпа­дают. Дифференцируя (*) по времени, имеем ; .

Теорема доказана.

Так как все точки движутся идентично. То в качест­ве кинематических характеристик тела достаточно за­дать кинематические характеристики любой его точки, т.е. задачи кинематики поступательного движения тела сводятся к задачам кинематики точки.

3.2 Вращение твердого тела вокруг неподвижной оси

Это движение, при котором все точки тела движутся по окружностям, центры которых лежат на оси вращения.

П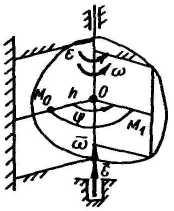 оложение тела задается двугранным углом  (углом поворота).

 =  (t) - уравнение движения.

Кинематические характеристики те­ла:

- угловая скорость, с^-1;

- угловое ускорение, с^-2.

Величины  и  можно представить в виде векторов , расположенных на оси вращения, направление вектора таково, что с его конца враще­ние тела видно происходящим против часовой стрелки. Направление совпадает с , если >о.

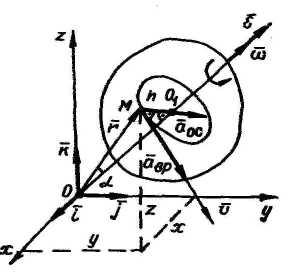П оложение точки тела: M₀M₁ = S = h.

Скорость точки ; при этом .

откуда ; ; .

Ускорение точки тела ,  ‑ вращательное ускорение (в кинематике точки – касательное ‑  ): - осестремительное ускорение (в кинематике точки - нор­мальное - ).

Модули: ; ; .

Равномерное и равнопеременное вращение

1. Равномерное:  = const, ; ;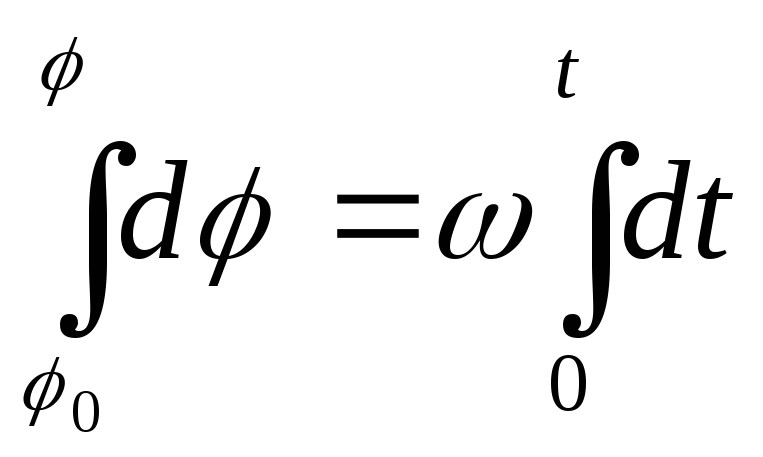 - уравнение движения.

2. Равнопеременное:  = const, ; ;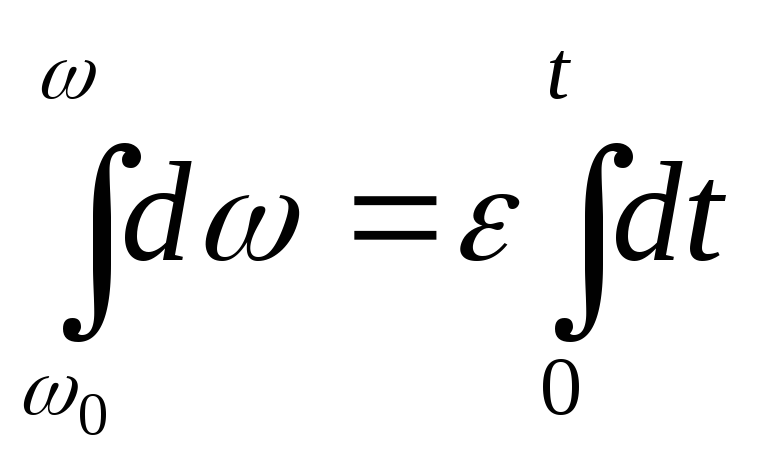 ; ; 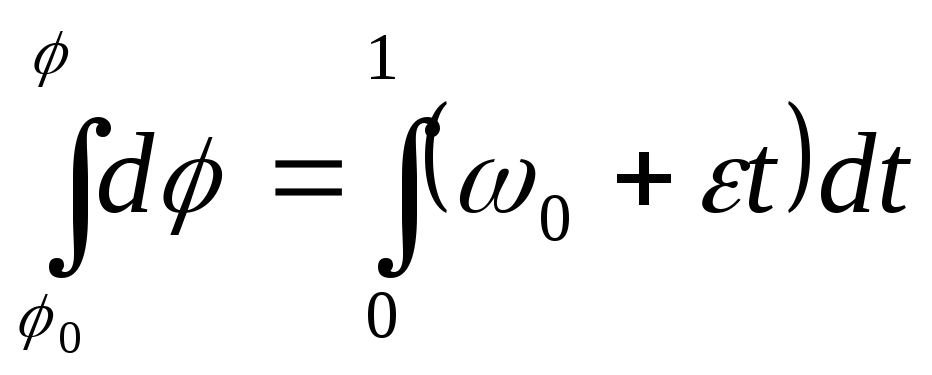- уравнение движения.

2 ). Механический привод состоит из шкива 1, ремня 2 и ступенчатых колес 3 и 4. Найти скорость рейки 5, а также ускорение точки M в момент времени t₁ = 1с. Если угловая ско­рость шкива равна ₁ = 0,2t , с^-1; R₁ = 15; R₃ = 40; r₃ = 5; R₄ = 20; r₄ = 8 (в сантиметрах).

Решение

Скорость рейки

;

; ; .

Откуда ; ; , с^-1.

Из (1) и (2) получим , см.

Ускорение точки M .

, с^-2 при t₁ = 1 с; a = 34,84 см/с².

3.3 Плоскопараллельное (плоское) движение твердого тела

Э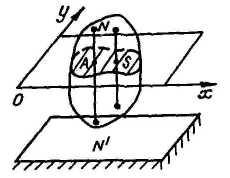 то движение, при котором все точки тела движутся в плоскостях, параллельных некоторой неподвижной пло­скости.

Все точки тела на любой прямой, перпендикулярной неподвижной пло­скости, движутся одинаково. Поэтому анализ плоского движения тела сво­дится к исследованию движения пло­ской фигуры (сечение S) в ее плоскости (xy).

Это движение можно представить как совокупность поступательного движения вместе с некоторой произвольно выбранной точкой а, называемой полюсом, и вращательного движе­ния вокруг полюса.

Уравнения движения плоской фигуры

x_а = x_a(t); у_а = у_а; j = j(t)

Кинематические характеристи­ки плоской фигуры:

- скорость и ускорение по­люса; w, e - угловая скорость и угловое ускорение (не зависят от выбора полюса).

У равнения движения любой точки плоской фигуры (B) можно получить, проектируя векторное равенство на оси x и у

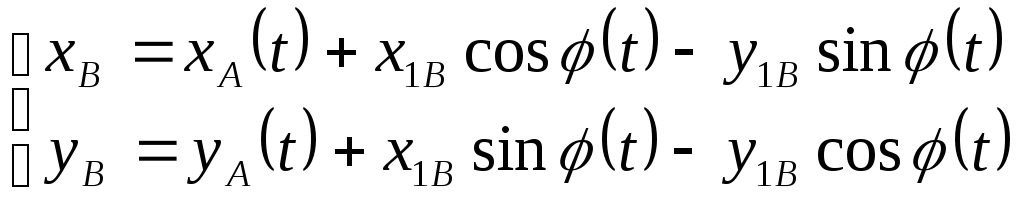
x_1B, y_1B - координаты точки в системе координат, свя­занной с фигурой.

Определение скоростей точек

1). Аналитический способ.

Зная уравнения движения x_n = x_n(t); y_n = y_n(t), находим ; ; .

2). Теорема о распределении скоростей.

Д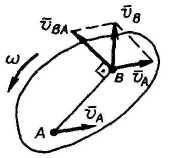 ифференцируя равенство , получим ,

- скорость точки B при вращении пло­ской фигуры вокруг полюса A; ;

Формула распределения скоро­стей точек плоской фигуры .

Пример

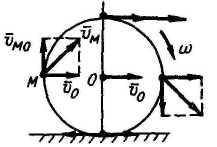
С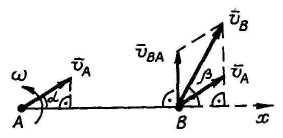 корость точки M колеса, катящегося без скольжения

; .

3). Теорема о проекциях ско­ростей.

Проекции скоростей двух то­чек тела на ось, проходящую че­рез эти точки, равны. Проектируя равенство на ось x, имеем

П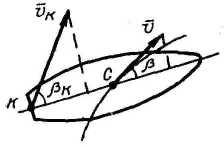 ример

Определить скорость натекания воды v_Н на руль корабля, если извест­ны (скорость центра тяжести суд­на), b и b_K (углы дрейфа).

Решение: .

4). Мгновенный центр скоростей (МЦС).

Скорости точек при плоском движении тела можно определять по формулам вращательного движения, используя понятие МЦС.

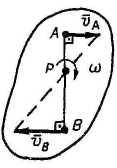
МЦС - точка, связанная с плоской фигурой, скорость которой в данный момент времени равна нулю (v_p = 0).

В общем случае МЦС - точка пере­сечения перпендикуляров к направле­ниям скоростей двух точек фигуры.

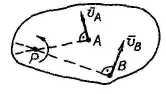
Принимая точку P за полюс, имеем для произвольной точки

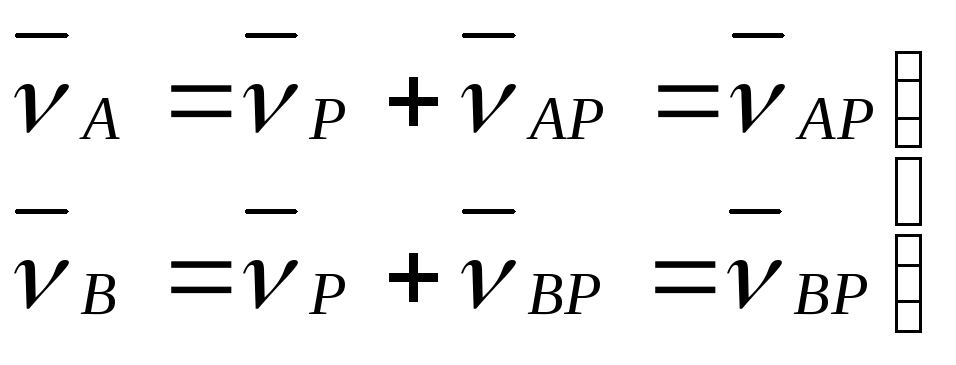, тогда

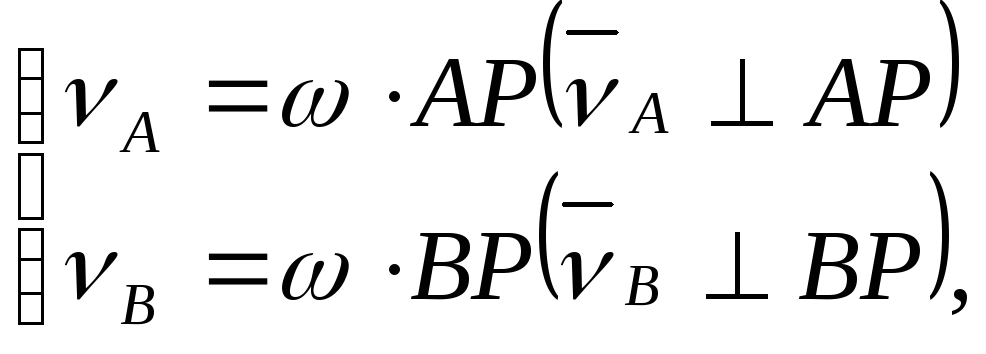
Откуда - угловая скорость фигуры и , т.е. скорости точек плоской фигуры пропор­циональны их расстояниям до МЦС.

Возможные случаи нахождения МЦС
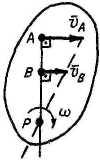
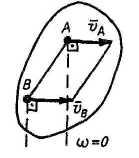
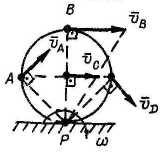
а		б	в Качение без скольжения
		МЦС - в бес­конечности

Случай б соответствует мгновенно поступательному распределению скоростей.

Примеры

1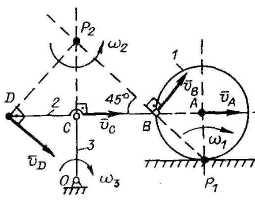 ). Для заданного положения механизма найти v_B, v_C,v_D, w₁, w₂, w₃, если в данный момент v_A = 20 см/с; BC = CD = 40 см; OC = 25 см; R = 20 см.

Решение МЦС катка 1 - точка P₁:

с^-1; см/с.

МЦС звена 2 - точка P₂ пересечения перпендикуляров к на­правлениям скоростей точек B и C:

с^-1; см/с; см/с; с^-1.

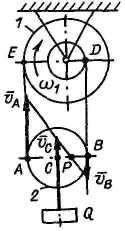
2). Груз Q поднимается с помощью ступенчатого бара­бана 1, угловая скорость которого w₁ = 1 с^-1; R₁ = 3r₁ = 15 см; AE || BD. Найти скорость v_C оси подвижного блока 2.

Решение

Находим скорости точек A и B:

v_A = v_E = w_1*R₁ = 15 см/с; v_B = v_D = w_1*r₁ = 5 см/с.

MЦС блока 2 - точка P. Тогда , откуда ; ; см/с.