Естественный способ задания движения

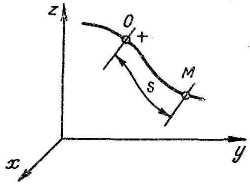
В этом способе считаются известными: 1) траектория движения; 2) начало отсчета о; 3) положительное и отрицатель­ное направления отсчета (+, -); 4) уравнение движения точки по траектории s = s(t).

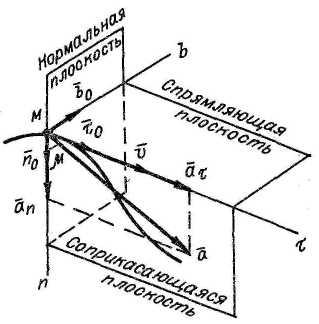
Скорость и ускорение точки определяются в проек­циях на оси естественного трехгранника:

t - касательная; n - главная нормаль; b - бинормаль; , , - орты этих осей; Скорость точки M (алгебра­ическое значение) .

Полное ускорение точки M равно векторной сумме касательного и нормального ускорений (а_b=0)

; ; .

Где r - радиус кривизны траектории в т. M.

Модуль ускорения

Направление .

Связь между координатным и естественным способами задания движения

Движение точки задано в декартовой системе координат x = x(t), у = y(t), z = z(t).

Касательное ускорение

.

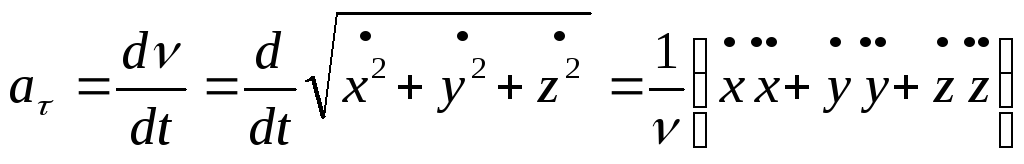Нормальное ускорение находится по формуле или из очевидного соотношения (приz=const)

.

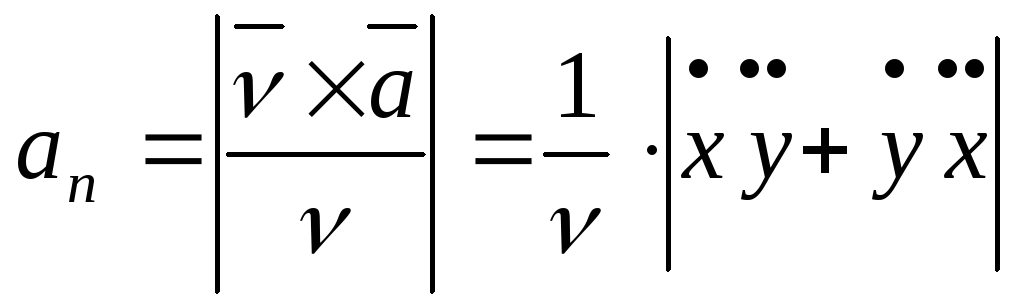Частные случаи движения точки

1. Равномерное прямолинейное движение (v = const; r = ¥)

; ;.

2. Равнопеременное пря­молинейное движение (at=const, r = ¥) ; ; ; .		Ускоренное
		Замедленное

3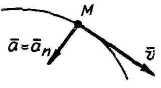. Равномерное криволинейное движение (v = const) ; ;.

4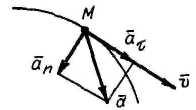. Равнопеременное криволинейное движение (а_т = const) ; ;

Примеры

1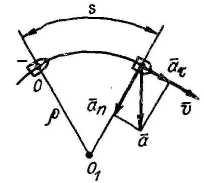). Судно движется равноускоренно на повороте ре­ки с радиусом закругления 1000 м и проходит путьS_k = 1000 м. Имея начальную скорость v₀ = 3,6 км/ч и конечную v_k = 18 км/ч, определить время движения t и ускорение судна в конце пути.

Решение

Так как движение равноускоренное, имеем

(1)

Найдем время t, подставляя значения S_k и v_k в (1), получим , откуда

2). Уравнения движения т. M: x = -6t² + 2; у = 2t. Найти уравнение траектории, а также положение точки, скорость, ускорение и его составляющие при t = 1 с. x и v - в метрах.

Решение

Уравнение траектории в координатной форме

.

Положение точки при

Скорость точки .

У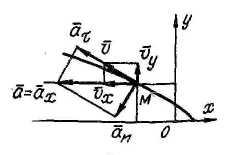скорение точки.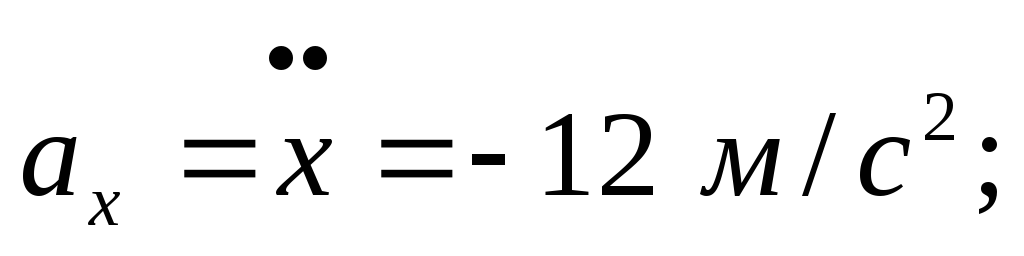

4). Частица грунта, слетающая с транспортера, движется с ускорением, проекции которого a_x = 0, а_у = g. Найти величину выдвига транспортера C, при котором частица упадет на расстоянии l = 7,5 м от борта баржи. Дано: H = 5 м; a = 30°; v₀ = 3,5 м/с; g = 9,8 м/с².

Р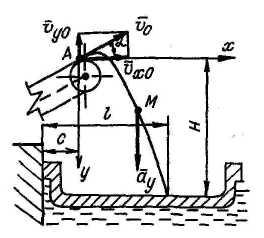ешение

Найдем уравнения движения час­тицы

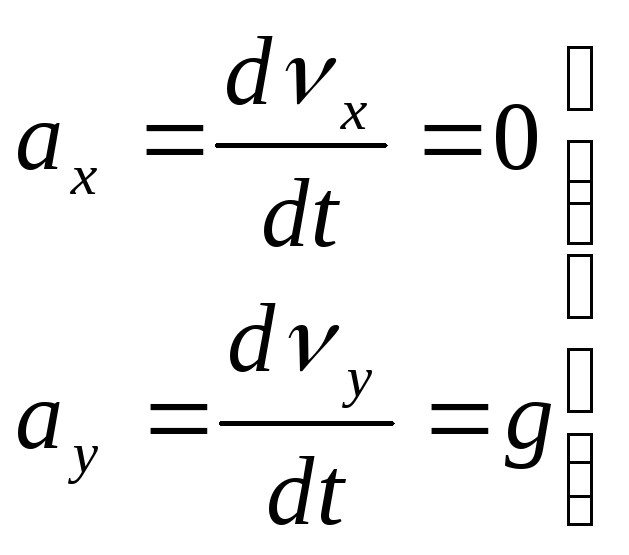
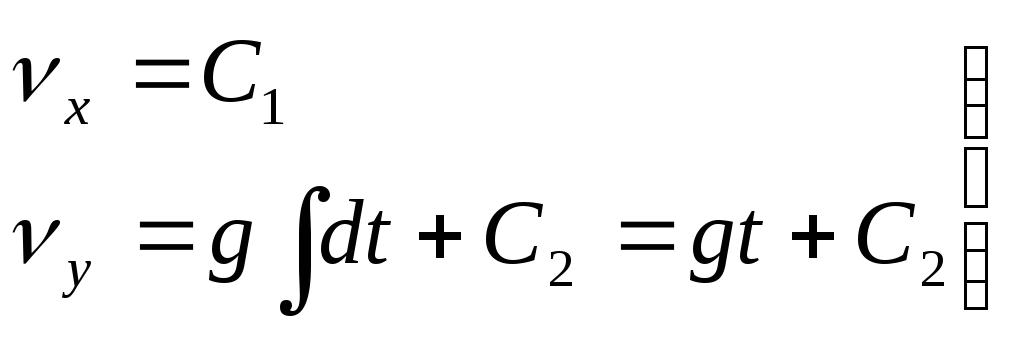(1)

Постоянные интегрирования C₁, C₂ определяем, подставляя в 1) началь­ные условия ;. Так как, имеем

.

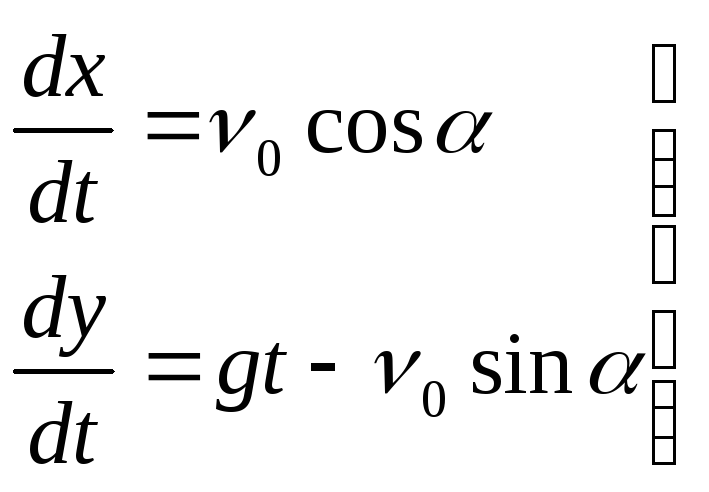
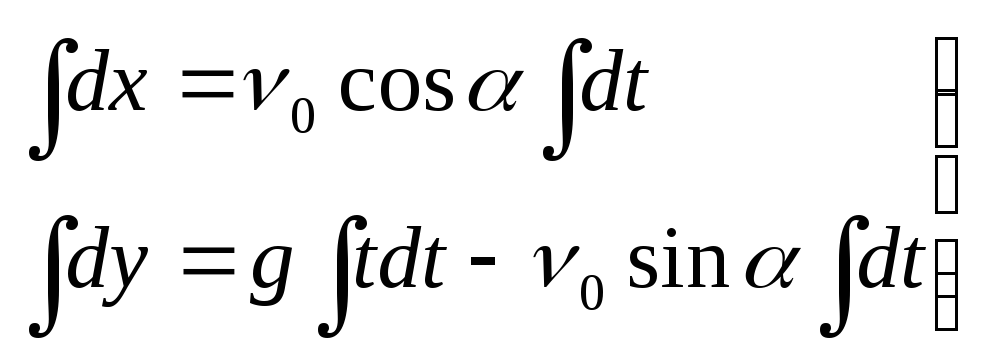
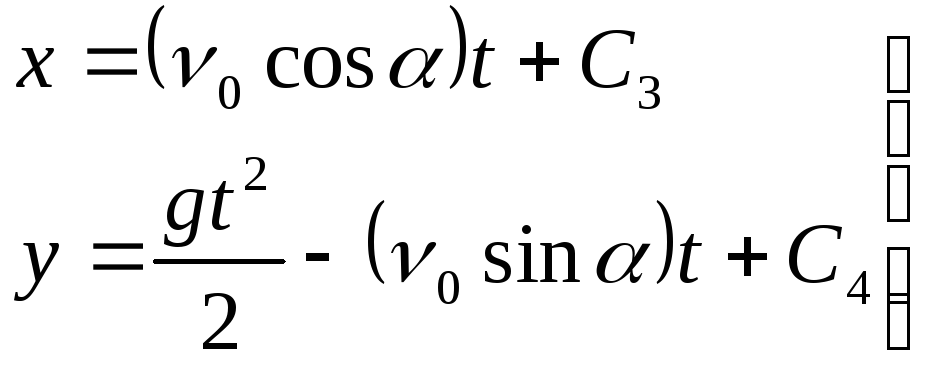Учитывая, что , получимC₃ = 0 и C₄ = 0. Окончательно уравнения движения частицы M примут вид 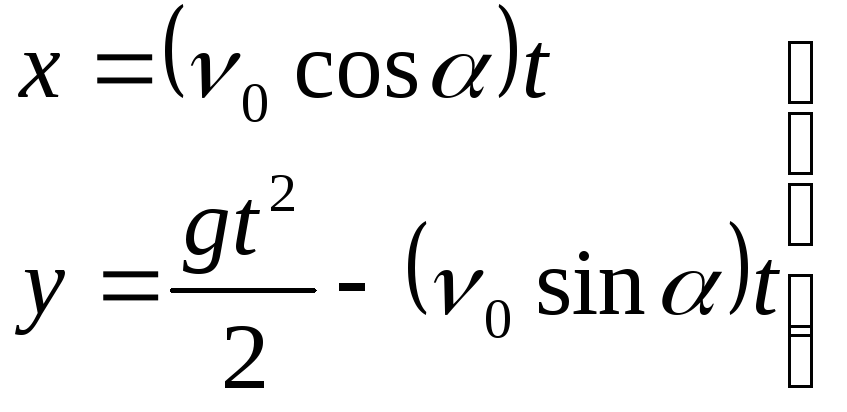.Исключая t, находим уравнение траектории в координатной форме (2).

По условию задачи при x = l - с y = H. Подставляя в (2), имеем (3).

Решая квадратное уравнение (3) при заданных значениях l, H, a,v₀, находим с = 3,85 м.

3 Кинематика твердого тела

Различают пять видов движения тела: поступатель­ное, вращение вокруг неподвижной оси. Плоскопараллельное, сферическое, свободное.

При изучении движения твердого тела кроме кинема­тических характеристик отдельных точек вводят кинематические характеристики тела в целом.

Рассмотрим, как определяются кинематические ха­рактеристики тела и отдельных его точек для этих ви­дов движения.

3.1 Поступательное движение твердого тела

Это такое движение, при котором любая прямая, про­веденная в теле, перемещается параллельно самой себе. Теорема: при поступательном движении все точки тела перемещаются по одинаковым траек­ториям и имеют в каждый момент равные (по величине и направлению) скорости и ускорения.

ИзAOB:

. (*)

Так как , то траектории точекA и B при наложении совпа­дают. Дифференцируя (*) по времени, имеем ;.

Теорема доказана.

Так как все точки движутся идентично. То в качест­ве кинематических характеристик тела достаточно за­дать кинематические характеристики любой его точки, т.е. задачи кинематики поступательного движения тела сводятся к задачам кинематики точки.