3.1.2. Вычисление обратной матрицы для системы линейных уравнений

Пусть дана невырожденная матрица , где (i, j = 1, 2,…,n). Для нахождения элементов обратной матрицы , где (i, j = 1, 2,…n) воспользуемся основным соотношением:

АА^-1 =Е, гдеЕ – единичная матрица.

Перемножая матрицы АиА^-1 и используя равенство их матрицеЕ, получимпсистем линейных уравнений вида:

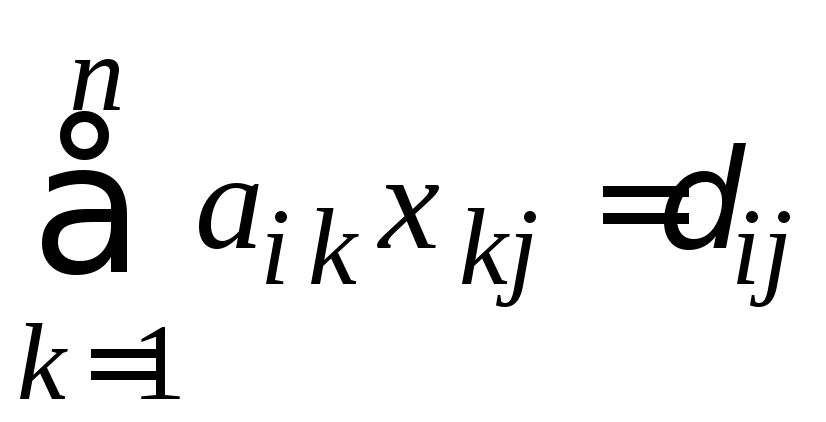(i = 1, 2, …, n; j – фиксировано), где.

Полученные псистем линейных уравнений имеют одну и ту же матрицуАи различные столбцы свободных членов. Эти системы можно решать методом Гаусса (см. п. 3.1.1). В результате решения систем получаем единичную матрицуA.

3.1.3. Метод простой итерации для систем линейных уравнений

Метод простой итерации даёт возможность получить последовательность приближённых значений, сходящуюся к точному решению системы.

Преобразуем систему (3.1) к нормальному виду:

.                                                 (3.2)

Правая часть системы (3.2) определяет отображение:

, преобразующее точку -мерного метрического пространства в точкутого же пространства.

Выбрав начальную точку , можно построить итерационную последовательность точекп- мерного пространства:

При определённых условиях данная последовательность сходится.

Так, для исследования сходимости таких последовательностей используется принцип сжимающих отображений, который состоит в следующем.

Если F – сжимающее отображение, определённое в полном метрическом пространстве с метрикой, то существует единственная неподвижная точка, такая, что. При этом итерационная последовательность,, полученная с помощью отображенияFс любым начальным членомх⁽⁰⁾, сходится к.

Оценка расстояния между неподвижной точкой отображенияF и приближениемх^(к)даётся формулами:

(3.3)

где α– множитель, определяемый достаточными условиями сжимаемости отображенияF.

Значение множителя α, определяется выбором метрики, в которой проверяется сходимость последовательности значений.

Рассмотрим Достаточные условия сходимости итерационной последовательности .

Практически, для применения метода итерации систему линейных уравнений удобно "погрузить" в одну из трёх следующих метрик:

(3.4)

Для того, чтобы отображение F, заданное в метрическом пространстве соотношениями (3.2), было сжимающим, достаточно выполнение одного из следующих условий:

а) в пространстве с метрикой :, т. е. максимальная из сумм модулей коэффициентов в правой части системы (3.2), взятых по строкам, должна быть меньше единицы.

б) в пространстве с метрикой :, т. е. максимальная из сумм модулей коэффициентов в правой части системы (3.2), взятых по столбцам, должна быть меньше единицы.

в) в пространстве с метрикой : , т. е. сумма квадратов при неизвестных в правой части системы (3.2) должна быть меньше единицы

Пример 3.1. Вычислить два приближения методом простой итерации. Оценить погрешность второго приближения. В качестве начального приближения выбрать .

Так как диагональные элементы системы являются преобладающими, то приведем систему к нормальному виду:

Последовательные приближения будем искать по формулам:

Получаем:

, .

Для оценки погрешности в метрике вычисляем коэффициент

.

Вычисляем погрешность: