2.7. Расчёт основных характеристик смо на основе использования их аналитических моделей

Рассмотрим такие СМО, в которых возможные состояния системы образуют цепь и каждое состояние, кроме исходного и последнего, связано прямой и обратной связью с двумя соседними состояниями. Такая схема процесса, протекающего в системе, называется схемой «гибели и размножения». Термин ведёт начало от биологических задач, процесс описывает изменение численности популяции.

Если в такой системе все потоки, переводящие систему из состояния в состояние пуассоновские, то процесс называется марковским случайным процессом «гибели и размножения».

Заметим, что в таких системах все состояния являются существенными, а значит, существуют финальные вероятности состояний, которые можно найти из линейной системы уравнений Эрланга.

На практике значительная часть систем (СМО) может описываться в рамках процесса «гибели и размножения».

Рассмотрим некоторые типы таких систем:

а) одноканальные с отказами (без очереди);

б) одноканальные с ограниченной очередью;

в) многоканальные с отказами (без очереди);

г) многоканальные с ограниченной очередью.

Одноканальные системы с отказами

Рассмотрим одноканальную систему обслуживания с отказом,

т. е. если поступает заявка на обслуживание, а устройство занято, то заявка получает отказ в обслуживании. Граф системы (рис. 2.5) имеет два состояния S₀ – устройство свободно и S₁ – устройство занято. Пусть интенсивность входящего потока равна λ (количество заявок в ед. времени), а интенсивность обслуживания равна µ.

Рис. 2.5. Граф одноканальной системы без очереди

Для изображённого графа система уравнений Эрланга имеет вид:

Из неё находим:

Основные характеристики системы M/M/1:

вероятность отказа P_отк = Р₁ = λ / (λ + µ);

вероятность обслуживания Р_обс = 1 – P_отк = µ / (λ+µ).

Одноканальные системы с ограниченной очередью

Рассмотрим теперь случай, когда устройство одноканальное, но если оно занято, то заявка не получает отказ, а становится в очередь к устройству. Очередь имеет длину не более n мест. Соответственно, граф состояний (см. рис. 2.6) будет иметь n + 1 вершину: состояние S₀ – устройство свободно; S₁ – устройство занято, нет очереди; S₂ – устройство занято, 1 в очереди; S_n+1 – устройство занято, n заявок в очереди.

Рис. 2.6. Граф одноканальной системы с очередью

Для такого графа система Эрланга имеет вид:

Из неё последовательно выражая все Р_k через Р₀ и подставляя в последнее нормировочное уравнение, имеем:

Основные характеристики системы M/M/1 / n:

вероятность отказа P_отк = Р_n+1 = (λ/µ)ⁿ⁺¹P₀;

вероятность обслуживания (относительная пропускная способность) Q = Р_обс=1 – P_отк ;

абсолютная пропускная способность А = λQ;

среднее число мест в очереди N = P₂ + 2P₃ + 3P₄ +…nP_n+1 .

Многоканальные системы с отказами

Рассмотрим случай, когда устройство многоканальное, количество каналов равно m. Если все каналы заняты, то заявка получает отказ. Граф состояний будет иметь m + 1 вершину (см. рис. 2.7): состояние S₀ – устройство свободно; S₁ – один канал занят; S₂ – два канала занято; S_m – m каналов занято.

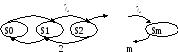
Рис. 2.7. Граф одноканальной системы с очередью

Обратите внимание, что интенсивность выходящих потоков кратна µ, например, при переходе из состояния S₂ в состояние S₁ интенсивность потока равна 2µ, т. к. если были заняты два канала, а затем стал занят один, то неизвестно какой из них освободился: µ + µ = 2µ.

Для этого графа построим систему уравнений Эрланга:

Выражаем все Р_k через Р₀ и подставляем в последнее нормировочное уравнение:

Основные характеристики системы M/M/m:

вероятность отказа P_отк = Р_m = 1/m! (λ/µ)^mP₀;

вероятность обслуживания Q =Р_обс=1– P_отк ;

абсолютная пропускная способность А= λQ;

среднее количество занятых каналов К = P₁ + 2P₂ + 3P₃ +…mP_m .

Количество каналов можно вычислить проще, зная соотношение

А = µК : среднее число заявок, обслуженных в единицу времени, равно произведению средней производительности одного канала на среднее число занятых каналов.