
- •Фгбоу впо «Кубанский государственный аграрный университет»
- •Курсовая работа
- •Реферат
- •Введение
- •1.1 Правила вывода
- •1.2 Проблема разрешения
- •1.3Конъюнктивная нормальная формула
- •1.4 Непротиворечивость исчисления высказываний
- •2. Проблема полноты в теории
- •2.1 Проблема полноты в узком смысле
- •Заключение
Министерство сельского хозяйства Российской Федерации
Фгбоу впо «Кубанский государственный аграрный университет»
(КубГАУ)
Кафедра компьютерных технологий и систем
Курсовая работа
По дисциплине: математическая логика и теория алгоритмов
На тему: «Проблемы непротиворечивости, полноты, разрешимости теории»
Студент: Елисеенко Дмитрий Игоревич
Специальность: Информационные системы и технологии
Группа: ИТ 1301
Краснодар 2014г.
Оглавление
Реферат
Ключевые слова: математическая логика, теории высказываний, непротиворечивость
Цель работы – изучить применение теорий неполноты, непротиворечивости разрешимости на практике.
В результате проведенной работы были изучены и применены на практике теории неполноты, непротиворечивости и разрешимости, а также различные виды высказываний.
Введение
Перед тем, как перейти к рассмотрению проблемы полноты в исчислении высказываний, необходимо дать описание тех объектов, с которыми придется столкнуться далее.
В качестве основного объекта исследования выступают тавтологии или тождественно истинные формулы. Множество всех тавтологий обозначим через Т. В терминах исчисления высказываний тавтологии следовало бы называть теоремами, но в силу его полноты и непротиворечивости эти понятия равнозначны. Причем для операций ˅ и ˄ вводится дополнительное соглашение: конъюнктам и дизъюнктам вида
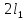 ∧
∧ ∧ … ∧
∧ … ∧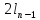
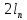 и
и
 ˅
˅ ˅ … ˅
˅ … ˅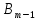 ˅
˅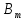
соответствуют формулы
(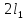
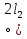 ˄ … ˄ (
˄ … ˄ (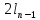 ˄
˄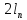 )))
и (
)))
и (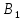 ˅ (
˅ (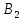 ˅ … ˅ (
˅ … ˅ (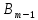 ˅
˅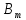 ))).
))).
 Данную
расстановку скобок будем называть
стандартной.
Данную
расстановку скобок будем называть
стандартной.
Следующим не менее важным объектом исследования выступают правила вывода, позволяющие из тавтологий снова получать тавтологии:
1)Правило
подстановки. Пусть
 – тавтология, содержащая переменное
высказывание Х, а В – произвольная
формула логики высказываний. Тогда если
заменить в
– тавтология, содержащая переменное
высказывание Х, а В – произвольная
формула логики высказываний. Тогда если
заменить в
 все вхождения Х на В, то полученная
формула тоже будет тавтологией.
все вхождения Х на В, то полученная
формула тоже будет тавтологией.
2) Правило заключения или modus ponens. Есть формулы 2l и 2l → B – тавтологии, то формула В тоже тавтология.
Следует сказать несколько слов по поводу правила подстановки. Можно вовсе убрать из рассмотрения данное правило, если ввести соглашение считать каждую формулу целым классом или схемой формул, получающихся из данной, путем подстановки вместо переменных высказываний всевозможных формул логики высказываний.
1.1 Правила вывода
Итак,
у нас есть тавтологии или теоремы, и
есть правила вывода, позволяющие из
одних тавтологий получать другие. Тогда
встает вопрос, можно ли из некоторого
узкого класса тавтологий посредством
правил вывода получить все тавтологии
из Т? Данный вопрос носит название
полноты проблемы. При этом систему
тавтологий, обладающую данным свойством
называют полной системой, а сами
тавтологии - аксиомами. Проблема полноты
является частным случаем проблемы
выразимости. Последняя состоит в указании
всех таких пар
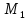 и
и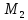 ,
что
,
что
 ,
,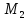 ≡ Т и
≡ Т и выразимо через
выразимо через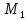 ,
т.е все тавтологии из
,
т.е все тавтологии из можно получить с помощью применения
правил вывода к тавтологиям, принадлежащим
можно получить с помощью применения
правил вывода к тавтологиям, принадлежащим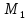 .
.
При
рассмотрении проблемы полноты удобно
ввести понятие оператора замыкания J,
порожденного правилами вывода . Пусть
M
≡ T
некоторое подмножество тавтологий.
Обозначим через М множество тавтологий,
которые либо принадлежат М, либо получены
с помощью однократного применения
правил вывода к тавтологиям, принадлежащим
М. Определим множества
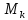 ≡T
индукцией по k:
≡T
индукцией по k:
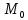 =
М
=
М
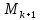 =
[
=
[ ]
]
Тавтологии, из которых выводятся все другие тавтологии, в исчислении высказываний принято называть аксиомами. В частности, выше приведена полная непротиворечивая система аксиом для исчисления высказываний.
Проблема полноты в терминах оператора замыкания J или проблема J-полноты выглядит следующим образом: для произвольной системы тавтологий М из Т требуется выяснить, является ли она J-полнотой в Т, то есть J(M) = T. Данная проблема эквивалентна задаче описания всех подмножеств М, которые являются J-полными в Т, последняя является частным случаем решения проблемы выразимости.
В
качестве основного подхода к решению
проблемы полноты используется подход,
основанный на получении критериев
полноты в терминах предполных классов.
Принцип определения критериев зависит
от свойств структуры замкнутых подмножеств
рассматриваемого множества. В нашем
случае произвольное подмножество
тавтологий М будем называть замкнутым
классом относительно оператора J
или просто J-замкнутым
классом, если J(M)
= M.
Основным понятием в данном подходе
служит понятие критериальной системы.
Оно определяется следующим образом:
пусть
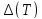 – совокупность всех замкнутых подмножеств
множества Т. ПосколькуJ(T)
= T,
то
– совокупность всех замкнутых подмножеств
множества Т. ПосколькуJ(T)
= T,
то
 не пуст. Критериальной системой называется
произвольное подмножество
не пуст. Критериальной системой называется
произвольное подмножество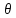 ,
,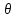
 ,
обладающее свойством: всякое множество
М тавтологий Т является полным тогда и
только тогда, когда для любого элементаQ,
Q
,
обладающее свойством: всякое множество
М тавтологий Т является полным тогда и
только тогда, когда для любого элементаQ,
Q

 ,
выполнено соотношение М
,
выполнено соотношение М Q.
Для применения критериальной системы
при исследовании множеств на полноту,
хотелось бы, чтобы она в некотором роде
была минимальной. Это объясняется тем,
что если
Q.
Для применения критериальной системы
при исследовании множеств на полноту,
хотелось бы, чтобы она в некотором роде
была минимальной. Это объясняется тем,
что если
 – критериальная система и в ней найдутся
такие элементы
– критериальная система и в ней найдутся
такие элементы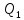 и
и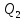 ,
что
,
что ⊆
⊆
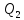 ,
то множество
,
то множество \
\ также будет критериальной системой.
Рассмотрение критериальной системы с
этой точки зрения приводит к понятию
предполного класса. Определим его
следующим образом:J-замкнутый
класс тавтологий М будем называть
J-предполным,
если J(M)
≠ T
и, при добавлении к М любой тавтологии
из Т \ М, получается J-полная
система. Непосредственно из определения
предполного класса следует, что каждый
предполный класс содержится в критериальной
системе. Если через
также будет критериальной системой.
Рассмотрение критериальной системы с
этой точки зрения приводит к понятию
предполного класса. Определим его
следующим образом:J-замкнутый
класс тавтологий М будем называть
J-предполным,
если J(M)
≠ T
и, при добавлении к М любой тавтологии
из Т \ М, получается J-полная
система. Непосредственно из определения
предполного класса следует, что каждый
предполный класс содержится в критериальной
системе. Если через
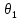 обозначить множество предполных классов,
то пол неизбыточностью критериальной
системы
обозначить множество предполных классов,
то пол неизбыточностью критериальной
системы можно считать представление ее в виде
можно считать представление ее в виде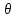 =
=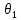
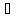
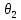 ,
где во второе слагаемое
,
где во второе слагаемое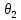 входят только такие замкнутые классы
из
входят только такие замкнутые классы
из ,
которые не являются подмножествами ни
одного из предполных классов. Если
определить приведенную критериальную
систему, как систему, не содержащую
собственных подсистем, являющихся
критериальными, то справедливы теоремы.
,
которые не являются подмножествами ни
одного из предполных классов. Если
определить приведенную критериальную
систему, как систему, не содержащую
собственных подсистем, являющихся
критериальными, то справедливы теоремы.
