Механика деформируемого твердого тела
.pdf
Кручение призматических тел
Пусть к основаниям однородного изотропного призматического тела приложены силы, приводящиеся к скручивающим парам. Будем считать, что объемные силы отсутствуют, и боковая поверхность призмы свободна от внешних сил.
Направим осьOx3 параллельно образующей боковой поверхности, а
осиOx1 иOx2 возьмем на одном из оснований бруса.
Решение задачи находится с помощью полуобратного метода, предложенный Сен-Венаном, в котором решение поставленной проблемы удается получить в перемещениях.
Будем считать, что каждое из сечений рассмотренной призмы поворачивается на малый угол, прямо пропорциональный расстоянию от нижнего основания
ψ=τ .x3 , где τ – постоянная величина, называемая степенью
В этом случае компоненты вектора перемещений можно выписать в явном
виде: |
u1 |
= −τ x2 x3,u2 |
=τ x1x3,u3 =τφ(x1,x2 ). |
|
Вычисляя компоненты тензора деформации и подставляя последние в формулы закона Гука, получаем выражения для компонентов тензора напряжений:
σ11 =σ22 =σ33 =σ12 = 0,
σ13 = μτ( ∂φ − x2 ),σ23 = μτ( ∂φ + x1 ). ∂x1 ∂x2
Формула Прандтля
Касательные напряжения, приложенные в поперечном сечении, сводятся к паре сил
с моментом
M = ∫(x1σ23 − x2σ13 )dω.
ω
Внося сюда значения касательных напряжений, окончательно получим M = Dτ, где
D = μ∫(x12 + x22 + x1 |
∂φ |
− x2 |
∂φ |
)dω. |
|
|
|||
ω |
∂x2 |
∂x1 |
||
Величина D называется жесткостью при кручении, D > 0
Введем гармоническую функцию ψ (x1 x2 ), сопряженную с функцией φ(x1 x2 ),
Граничное условие для функции ψ будет иметь вид
∂ψ |
dx2 |
+ |
∂ψ |
dx1 |
−(x |
|
dx2 |
+ x |
dx1 |
) = 0. |
|
|
2 dl |
|
|||||||
∂x dl |
|
∂x dl |
|
1 |
dl |
|||||
2 |
|
|
1 |
|
|
|
|
|
|
|
Для компонентов тензора напряжений получим формулы
σ13 = μτ(∂ψ − x2 ),σ23 = −μτ(∂ψ − x1 ). ∂x2 ∂x1
Часто вместо функции ψ вводят другую функцию Φ(x1,x2 ) , называемую функцией напряжений при кручении или функцией напряжений Прандтля. Она определяется формулой
Φ(x1,x2 ) =ψ (x1, x2 ) − 12 (x12 + x22 ).
В этом случае имеем |
|
|
∂Φ ,σ |
|
= −μτ ∂Φ . |
σ |
13 |
= μτ |
23 |
||
|
|
∂x2 |
∂x1 |
||
|
|
|
|
||
Первая формула преобразуется к виду |
M = 2μτ ∫Φdω и называется формулой |
||||
Прандтля. |
|
|
|
|
ω |
|
|
|
|
|
|
Аналогии при кручении Прандтля
Задача определения функции напряжений при кручении и задача нахождения прогиба однородной мембраны, равномерно натянутой на жесткий контур и нагруженной равномерным давлением, являются одной и той же математической
задачей, если контур, на который натянута мембрана, совпадает с контуром
поперечного сечения бруса.
Мембраной называется тонкая пленка, сопротивляющаяся только растяжению и не оказывающая сопротивления изгибу. Рассмотрим мембрану, равномерно натянутую на плоский жесткий контур L , совпадающий с контуром односвязного поперечного сечения скручиваемого бруса. Пусть q– растягивающее усилие, приходящееся в каждом сечении мембраны на единицу его длины, p – давление на единицу
площади мембраны, w(x1,x2 ) – перемещение точки срединной поверхности мембраны в направлении оси x3 , перпендикулярной плоскости контура.
Условие равновесия первоначально прямоугольного элемента мембраны в
деформированном состоянии приводит к уравнению равновесия элемента:
|
∂2 w |
+ |
∂2 w |
= − |
p |
. |
|||
|
∂x2 |
∂x2 |
q |
||||||
|
|
|
|
|
|
||||
|
1 |
|
2 |
|
|
|
|
|
|
|
Перемещения (прогибы) мембраны на жестком контуре L равны нулю, поэтому |
||||||||
|
граничное условие будет w(x1,x2 ) |L = 0. |
|
p |
|
|
|
|||
|
Если положить w = kΦ , то получим |
w = |
Φ. |
||||||
|
|||||||||
Следовательно, задача кручения может2qбыть решена путем измерения прогибов
равномерно нагруженной мембраны. Мембранная аналогия, предложенная
Прандтлем, позволяет наглядно представить характер функции напряжений, а также сделать заключение о распределении напряжений на поперечном сечении бруса.
Помимо мембранной аналогии Прандтля известны гидродинамические аналогии: аналогия Буссинеска с ламинарным течением вязкой жидкости, аналогия Гринхилла с вихревым течением идеальной несжимаемой жидкости и другие.
Задача: Призматический брус эллиптического профиля
Функция напряжения Прандтля Φ(x1,x2 ) должна быть постоянной на эллипсе
x2 |
+ |
x2 |
=1. |
|
1 |
2 |
|||
a2 |
b2 |
|||
|
|
Функция Φ(x1,x2 ), заведомо удовлетворяющая этому граничному условию, может быть представлена в виде
Φ(x ,x ) = A( |
x2 |
+ |
x2 |
), |
|
1 |
2 |
||||
a2 |
b2 |
||||
1 2 |
|
|
где A – неизвестная постоянная. Кроме того, эта функция должна внутри
эллипса удовлетворять уравнению Пуассона. Отсюда получаем
A = − a2 +b2 .
|
Тогда |
|
|
|
2 |
2 |
|
2 |
|
2 |
|
|
Φ(x ,x ) = − b |
x1 |
+ a |
x2 . |
|
||||||
|
|
|
1 |
2 |
|
a2 |
+b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Окончательно имеем: |
|
|
2a2 μτ |
x |
|
|
|
|
2b2 μτ |
x . |
|
σ |
|
= − |
|
,σ |
|
= − |
|
|||
|
|
|
|
|
|||||||
|
|
13 |
|
a2 +b2 2 |
|
23 |
|
|
a2 +b2 1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
Задача: Призматический брус с равносторонним треугольником в
сечении
Рассмотрим призматический брус, сечение которого представляет равносторонний треугольник с высотой h . Уравнения сторон треугольника
будут
x2 = 0,x2 = −
3x1 + h,x2 = 
3x1 + h.
Представим функцию напряжений Прандтля в виде
Φ(x1,x2 ) = Ax2[(x2 −h) + 
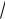3x1 ][(x2 −h) − 
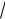3x1 ].
Эта функция на сторонах треугольника равна нулю. Кроме того, внутри треугольника она должна удовлетворять уравнению Пуассона.Отсюда
находим, что
|
A =1/2h |
|
|
|||||
Тогда |
Φ(x ,x |
) = |
1 |
x |
[(x |
− h)2 −3x2 |
]. |
|
2h |
||||||||
|
1 2 |
|
2 |
2 |
1 |
|
||
Окончательно имеем:
σ13 = μτ2h [3(x22 − x12 ) + h(h − 4x2 )],σ23 = 3μτh x1x2.
Одномерные линейные задачи динамической теории упругости
Рассмотрим систему дифференциальных уравнений, которая описывает
распространение волны сжатия в тонком упругом стержне:
ρ |
∂u |
= |
∂σ |
, |
∂σ |
= a |
∂u . |
|
∂t |
∂x |
∂t |
||||||
|
|
|
|
∂x |
Здесь u скорость частиц в направлении оси стержняx ; σ напряжение на
– – на
площадке, нормальной к оси стержня; известные функции переменной (постоянные в случае однородного стержня) ρ(x) ≥ ρ0 > 0 и a(x) ≥ a0 > 0 имеют смысл плотности среды и модуля Юнга соответственно. Первое уравнение представляет собой уравнение движения частиц среды, второе – почленно продифференцированный по переменной закон Гука.
К этой же системе уравнений можно прийти, рассматривая одномерную задачу о распространении упругих волн в изотропной полубесконечной среде x ≥ 0 , −∞ < y < ∞ , −∞ < z < ∞ , когда краевые условия при t = 0 и x = 0 не зависят от переменных y и z .
Мы имеем три независимые системы. Одна из них будет описывать распространение
плоской продольной волны сжатия, две другие – волны сдвига.
Эту систему уравнений часто записывают в виде
ρ ∂u |
+ ∂p |
= 0, |
∂p + ρc2 ∂u |
= 0. |
|
∂t |
∂x |
|
∂t |
∂x |
|
В этом случае ее называют системой уравнений акустики, она описывает распространение плоских звуковых волн. Величину p = −σ называют давлением в среде, c = a/ρ – скоростью звуковых волн.
Решение задачи
Если ρ и cпостоянны, то система уравнений имеет вид:
|
∂X +c |
∂X |
= 0, |
|
|
∂Y −c |
∂Y = 0, |
|
|
||||||
|
∂t |
∂x |
|
|
|
|
∂t |
|
∂x |
|
|
|
|
||
где введены обозначения |
X = u − |
σ |
,Y = u + |
σ |
. |
|
|
|
|
||||||
|
|
|
|
|
ρc |
|
|
|
ρc |
|
|
|
|
||
В случае переменных коэффициентов система полностью разделяется на два |
|||||||||||||||
независимых уравнения, только когда упругая среда имеет постоянную жесткость ρc. |
|||||||||||||||
Величины X и Y называются инвариантами Римана. Очевидно, что общее решение |
|||||||||||||||
полученных уравнений имеет вид |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
X = f (x −ct),Y =ϕ(x + ct), |
|
||||||||||
где f и ϕ – произвольные гладкие функции. Величины X |
и Y не изменяются |
||||||||||||||
соответственно вдоль линий x −ct =const и |
x +ct |
=const, которые называют |
|||||||||||||
характеристиками системы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для однозначного определения решения необходимо задать краевые условия. К |
|||||||||||||||
примеру, для решения задачи на отрезке l |
≤ x ≤ l |
2 |
нужно знать значения u и σ при |
||||||||||||
t 0 : u(x,0) = u0 (x),σ(x,0) =σ0 (x) |
|
|
|
|
1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
и некоторую линейную комбинацию u и σ при x = l1,x = l2 : |
|
||||||||||||||
|
(α1u + β1σ )x=l = f1 (t), |
(α2u + β2σ)x=l |
= f |
2 (t), |
|||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
(α |
/ρc − β ≠ 0,α |
2 |
/ρc + β |
2 |
≠ 0,α |
2 |
+ β 2 |
≠ 0,α2 |
+ β 2 |
≠ 0). |
|||||
1 |
1 |
|
|
|
|
1 |
1 |
|
2 |
2 |
|
||||
При этом, для определения u и σ в так называемом характеристическом треугольнике, ограниченном на плоскости x,t отрезками прямой t = 0 и характеристик x ± ct =const, проходящими соответственно через точки (l2 ,0)и (l1,0)
достаточно знания только начальных условий.
Двумерные линейные задачи динамической теории упругости
Пусть плоская область Ω представляет собой объединение прямоугольников со |
|
||||||||||||||||||||||||||||||||||||||
|
сторонами, параллельными осям декартовой системы координат |
x y. Динамическая |
|||||||||||||||||||||||||||||||||||||
|
задача теории упругости в декартовой системе координат формулируется |
|
|||||||||||||||||||||||||||||||||||||
|
следующим образом. |
u(x, y,t) |
|
v(x, y,t) |
σx (x, y,t) σ |
|
(x, y,t) τxy (x, y,t) |
|
|
|
|||||||||||||||||||||||||||||
|
Определить функции |
|
|
|
, |
|
|
|
, |
|
, |
|
|
y |
|
|
|
|
, |
|
|
, удовлетворяющие в |
|||||||||||||||||
|
области Ω системе дифференциальных уpавнений: |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
∂u |
|
∂σ |
|
|
∂τxy |
|
|
|
|
∂σx |
|
|
2 |
∂u |
|
∂v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
ρ |
|
= |
|
|
x |
+ |
|
|
|
, |
|
|
∂t |
|
= ρcp ( |
∂x |
+θ |
∂y |
), |
|
|
∂τxy |
|
|
|
∂u + |
∂v), |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
∂t |
|
|
∂x |
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
= |
ρc2 ( |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
∂σy |
|
|
|
|
|
∂u |
∂v |
|
|
|
|
|
|
|
|||||||||||||||
|
|
∂v |
|
∂τxy |
|
|
∂σy |
|
|
|
|
|
|
2 |
|
|
|
|
∂t |
|
|
|
|
s |
∂y |
∂x |
|
|
|
||||||||||
|
ρ |
= |
+ |
|
|
, |
|
|
∂t |
= ρcp (θ ∂x + |
∂y), |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
∂t |
|
∂x |
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
где в случае однородной среды – константы ρ,cp ,cs |
– соответственно плотность |
|
||||||||||||||||||||||||||||||||||||
|
среды, продольная и поперечная скорости упругих волн;θ =1−2c2 /c2. Неизвестные |
|
|||||||||||||||||||||||||||||||||||||
|
функции u |
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
p |
– |
||||
|
v – компоненты вектора скорости частиц упругой среды; σx ,σ y ,τxy |
||||||||||||||||||||||||||||||||||||||
|
нормальные и касательная компоненты тензора напряжений. |
|
|
|
|||||||||||||||||||||||||||||||||||
Иногда рассматривается наиболее простая модель упругой среды с нулевой |
|
||||||||||||||||||||||||||||||||||||||
|
сдвиговой жесткостью μ ( cs |
|
= 0, θ =1 ). В этом случае σx =σy =σ и система |
|
|||||||||||||||||||||||||||||||||||
|
уравнений вырождается в три уравнения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
∂u ∂σ |
|
∂v |
|
|
∂σ |
|
|
|
∂σ |
|
|
|
2 |
|
∂u ∂v |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
ρ |
|
|
= |
|
, |
|
ρ ∂t |
|
|
= |
|
, |
|
|
|
= |
ρcp |
( |
|
+ |
|
), |
|
|
|
|
||||||||
|
|
|
|
|
∂t |
|
∂x |
|
|
|
∂y |
|
|
∂t |
∂x |
∂y |
|
|
|
|
|||||||||||||||||||
которые называют системой уравнений двумерной акустики.
Начальные и граничные условия
Неизвестные функции должны удовлетворять начальным условиям:
u(x, y,0) = u (x, y),v(x, y,0) = v (x, y),σx (x, y,0) =σx (x, y),
σy (x, y,0) =σy (x, y),τxy (x, y,0) =τxy (x, y)
играничным условиям, одним из вариантов которых может быть следующий:
(a1u +b1σ |
x |
) | |
x=l |
= f 1, i =1,..., N, |
(c1u + d |
1τ |
) | |
y=l |
|
= g1 , j =1,..., M , |
|||||||||||||||
|
i |
|
|
|
i |
|
i |
|
|
j |
j xy |
|
j |
j |
|||||||||||
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(ai2v +bi2τxy ) |x=li |
= fi 2 , |
(c2j v + d 2j σy ) |y=l j |
= g2j , |
||||||||||||||||||||||
|
ais |
|
+ |
|
bis |
|
≠ 0, s =1, 2 |
|
cs |
|
|
+ |
|
d s |
|
|
≠ 0, s =1, 2 |
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
если участок границы параллелен оси y; участок границы параллелен оси х.
Если область Ω , в которой необходимо решать задачу, можно представить в виде объединения круговых цилиндров (сплошных либо полых) с единой осью, а свойства
среды, начальное состояние и внешнее воздействие одинаковы в каждом
проходящем через ось меридиональном сечении, мы можем сфоpмулиpовать так называемую осесимметpичную задачу в цилиндрической системе координат r,ϕ, z , где ось z совпадает с осью цилиндров.
Законы сохранения механической энергии
Энергетическое тождество – закон сохранения механической энергии записывается в виде
∫[ρu |
∂u |
+ ρv |
∂v |
+σx |
∂u |
+σy |
∂v |
+τxy |
( |
∂u |
+ |
∂v)]dω = |
|||
ω |
∂t |
|
∂t |
|
∂x |
|
|
|
∂y |
|
|
∂y |
|
∂x |
|
|
|
= ∫ |
[ |
∂(σxu +τxyv) |
+ |
∂(σyv +τxyu) |
]dω. |
||||||||
|
|
|
|
||||||||||||
|
|
ω |
|
|
∂x |
|
|
|
|
|
∂y |
|
|
|
|
Аналогичное тождество получается и для случая осесимметричной задачи:
∫[ρur |
∂ur |
+ ρuz |
∂uz +σr |
∂ur +σz |
∂uz |
+σϕ |
ur |
+τrz |
( |
∂ur + |
∂uz )]rdω = |
|||||
r |
||||||||||||||||
ω |
∂t |
|
|
∂t |
∂r |
∂z |
|
|
|
|
∂z |
∂r |
||||
|
= ∫[ |
∂(rσrur + rτrzuz ) |
+ |
∂(rτrzur + rσzuz ) |
]dω. |
|
||||||||||
|
|
|
|
|||||||||||||
|
ω |
|
|
∂r |
|
|
|
|
∂z |
|
|
|
|
|
|
|
При построении численного решения часто используются разностные аналоги этих тождеств.