
Механика деформируемого твердого тела
.pdf
Второй закон термодинамики
Критерий необратимости содержится во втором законе термодинамики, который постулирует существование двух дополнительных параметров состояния - абсолютной температуры T и энтропии S .
Согласно одной из формулировок второго закона термодинамики скорость изменения со временем полной энтропии ДТТ, занимающего объем V , никогда не может быть меньше, чем сумма притока энтропии через границу объема и энтропии, производимой внутри объема внешними источниками.
Полная энтропия определяется по формуле S = ∫ρsdv, где s удельная энтропия. |
|||
Согласно формулировке второго закона |
v |
||
|
|
|
|
ds2 |
= 0 |
при обратимых процессах, ds2 > 0 при необратимых процессах |
|
dt |
ds2 |
dt |
|
где |
dt |
- скорость изменения энтропии, вызванная внутренними изменениями |
|
При обратимых процессах скорость изменения плотности энтропии связана с температурой соотношением dq T ds
dt = dt
Математически закон сохранения энтропии выражается в интегральной форме в виде неравенства Клаузиуса – Дюгема
d ∫ρsdv ≥ ∫ρedv− ∫cini ds |
||
dt v |
v |
s T |
где e – мощность локальных внешних источников энтропии, ci - поток тепла через
единицу площади в единицу времени. Это соотношение постулирует, что внутреняя энтропия в объеме не убывает.

Замкнутая система уравнений
Для термомеханической среды, где механические и тепловые явления взаимосвязаны, основными уравнениями в эйлеровых координатах будут следующие:
- Уравнение неразрывности:
ρ |
|
|
∂v |
|
d |
+ |
ρ |
|
k = 0 |
dt |
|
|||
|
|
∂xk |
||
- Три уравнения движения:
ρdvi = ∂tij + ρF dt ∂x j i
|
- Уравнение энергии: |
du = |
1 |
tij vij − |
1 |
|
|
∂ci |
|
|
|
|
||||
|
|
ρ |
ρ ∂xi |
|
|
|
||||||||||
|
|
dt |
|
|
|
|
|
|
|
|||||||
|
В дополнение к этому должно быть выполнено неравенство |
|||||||||||||||
|
Клаузиуса – Дюгема: |
ρ ds ≥ ρe − 1 ∂ci |
|
+ ci |
|
∂T |
||||||||||
|
|
dt |
|
|
T |
|
∂xi |
|
|
|
T2 |
|
∂xi |
|
||

Определяющие уравнения
Назначение этих уравнений состоит в том, чтобы установить математические соотношения между параметрами состояния, описывающими поведение материала при наличии механических и термодинамических воздействий.
Определяющие уравнения вводят в рассмотрение некоторые
идеализированные среды, которые называют моделями сред, отражающие поведение реальных тел в определенном интервале нагрузок и температур.
Теория определяющих уравнений основывается на некоторых общих
вытекающих из опыта принципах. Рассмотрим три из них, известных как
система аксиом Нолла.
Первая аксиома называется принципом детерминизма и постулирует, что напряженное состояние в некоторой фиксированной точке тела (описываемое тензором напряжения) полностью определяется историей движения тела до текущего момента времени.
Вторая аксиома формулирует ограничение, называемое принципом локального действия, который постулирует, что в напряженное состояние в точке среды оказывают влияние лишь процессы, протекающие в бесконечно близких к ней точках.
Естественно потребовать, чтобы определяющие уравнения не зависели от выбора системы координат. Это требование постулируется третьей аксиомой, которая называется принципом материальной независимости (индифферентности) от системы отсчета. Распространение данного принципа на преобразование по времени, приводит к требованию независимости определяющих уравнений от времени явно.

Уравнения состояния
Один из способов получения уравнений состояния ДТТ - постулирование существования полного дифференциала у плотности внутренней энергии.
Например, пусть плотность внутренней энергии записывается в виде u = u(Aij ,s)
где Aij - тензор деформации Альманси, s - плотность энтропии. Дифференциал от
плотности имеет вид |
∂u |
|
∂u ds |
|
du = |
dAij + |
|||
∂Aij |
||||
|
|
∂s |
||
Для обратимых процессов имеем |
dq |
ds |
|
|
|
dt = T dt |
|
||
В этом случае локальная форма уравнения энергии запишется в виде
|
|
|
du |
= |
1 tij vij + T ds |
|
Учитывая, что |
vij = |
dAij |
dt |
|
ρ |
dt |
|
|
|
|
|||
dt |
|
|
|
|||
|
|
|
|
|
||
получим |
|
|
du = 1 tijdAij + Tds |
|||
|
|
|
|
|
ρ |
|
Получим уравнения состояния ДТТ:
tij = ρ |
∂u |
T = ∂u |
|
∂Aij |
|||
|
∂s |
В случае бесконечно малых деформаций напряжения в первом соотношении имеют потенциал. Другие формы записи определяющих уравнений ДТТ получаются, если вместо внутренней энергии ввести новые термодинамические функции – свободная энергия или потенциал Гиббса.

2. Основы теории упругости

Основные определения
Твердые тела под действием приложенных к ним нагрузок изменяют свою форму и размеры. Если деформация тела сравнительно мала, то при снятии внешних сил тело возвращается в начальное
недеформированное состояние. Способность тела восстанавливать
свою первоначальную форму и размеры при устранении внешних воздействий называют упругостью, а снимаемые при этом деформации
– упругими.
В дальнейшем будем рассматривать только малые обратимые деформации твердого тела.
Твердое тело называют идеально упругим, если напряженное состояние в любой его точке в произвольный момент деформирования зависит только от деформации в этой точке.
Результаты экспериментов показывают, что в определенных пределах нагружения для большинства твердых тел деформации пропорциональны нагрузкам, т.е. увеличение нагрузки приводит к увеличению деформации в том же отношении. Эта закономерность известна как закон Гука.
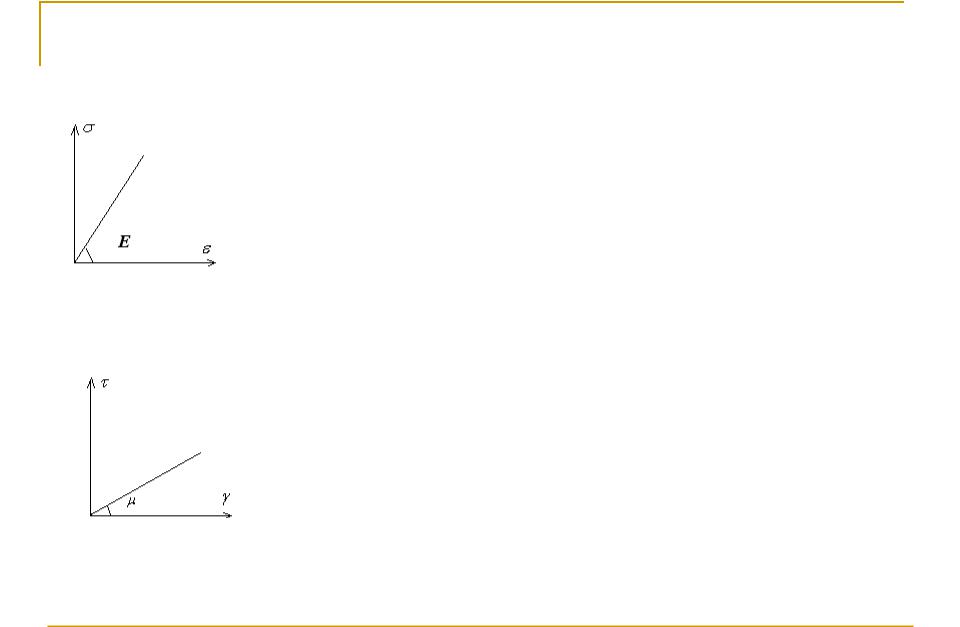
Модуль Юнга. Модуль сдвига
Диаграмма одноосного
растяжения
На рисунках приведены идеализированные
результаты наиболее легко осуществимых
экспериментов по простейшему нагружению образцов – испытанию при одноосном растяжении (верхний рисунок) и испытанию трубчатых образцов
на кручение (нижний рисунок).
В первом случае в тонком образце реализуется простейшее напряженное состояние – одноосное растяжение, во втором – чистый сдвиг.
Коэффициент пропорциональности между напряжениемσ и деформацией ε называют
модулем Юнга E :
σ = Eε, |
(2.1) |
а коэффициент пропорциональности между |
|
касательным напряжениемτ |
и сдвигом γ – |
модулем сдвига μ : |
|
Вообще говоря, величины E и μ следует считать
независимыми.
Диаграмма чистого сдвига

Коэффициент Пуассона
Рассмотрим процесс деформирования элементарного параллелепипеда в
системе координат, совпадающей с главными осями. На три его взаимно перпендикулярные грани действуют напряженияσ1 ,σ2 ,σ3 . Пусть напряженияσ2
иσ равны нулю, тогда деформацияε1 , согласно закону Гука для случая
=σ1/E. Испытывая удлинение в первом3 ε1одноосного растяжения, равна
направлении, параллелепипед будет сжиматься в двух других направлениях. Безразмерный параметр, характеризующий эту степень сжатия, называют
коэффициентом Пуассона .
Действие напряжения σ1 вызовет деформации ε1 = E1 σ1 − νE σ2 − νE σ3 = 1+Eν σ1 − 3Eν σ, Здесь σ = (σ1 +σ2 +σ3 )/3 - среднее напряжение. Аналогично получаем уравнения для напряженийσ 2 и σ3 . Эти равенства можно записать как:
ε |
ij |
= 1+ν |
σ |
ij |
− 3ν |
σδ |
. |
(2.2) |
|
E |
|
E |
ij |
|
ν |
||
|
|
|
|
|
|
|||
Связь между модулем сдвига μ , модулем Юнга E |
и коэффициентом Пуассона |
|||||||
имеет вид: |
|
E |
= μ. |
|
|
|
||
|
|
|
|
|
||||
|
2(1+ν) |
|
|
|
||||
|
|
|
|
|
|
|
||
В силу того, что величины μ и E положительны, получим ограничение для
коэффициента Пуассона ν ≥ −1.
Таким образом, касательные напряжения пропорциональны недиагональным компонентам тензора деформации:
σij = 2μεij ,i ≠ j.

Модуль объемного сжатия. Параметры Ламе
Вычислим первый инвариант тензора деформации θ = ε11 +ε22 +ε33 :
ε11 +ε22 +ε33 |
= |
(1+ν) |
(σ11 +σ22 |
+σ33 ) − |
9ν |
σ = |
3(1− 2ν ) |
σ. |
|
E |
E |
E |
|||||||
|
|
|
|
|
|
Таким образом, среднее напряжение и относительное изменение объема
пропорциональны: σE= Kθ.
Коэффициент K = 3(1−2ν) называют модулем объемного сжатия.
В силу того, что величина K по своему физическому смыслу обязана быть
неотрицательной, на коэффициент Пуассона накладывается ограничение
сверху: |
ν ≤ |
1 . |
|
|
2 |
Зависимости (2.2) называют обратной формой закона Гука для изотропной упругой среды.
Зависимости между компонентами девиаторов тензоров запишутся в виде
|
Тогда |
|
|
|
σij′ = 2μεij′, |
σ = Kθ. |
|
|
|
||||||||
|
|
σ |
|
=σ ′ +σδ |
|
= 2μ(ε |
|
− |
1 |
θδ |
|
) + Kθδ |
|
= |
|||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
ij |
ij |
|
ij |
|
ij |
2 |
3 |
|
ij |
|
ij |
|
|
|
|
|
|
|
|
= 2μεij +(K − |
3 |
μ)θδij . |
|
|
|||||||
|
Величина λ = K − |
2 |
μ носит название параметра Ламе. |
||||||||||||||
3 |
|||||||||||||||||
Окончательно определяющие уравнения имеют вид: |
|||||||||||||||||
|
|
|
|
|
|
σij = λθδij |
+ 2μεij . |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Основные уравнения
Напряженное состояние характеризуется шестью |
|
независимыми компонентами симметричного тензора |
|
напряжений σij , которые должны удовлетворять трем |
|
дифференциальным уравнениям равновесия: |
|
∂σij + Pi = 0. |
(2.3) |
∂x j |
|
Компоненты тензора напряжений связаны с компонентами тензора деформаций шестью линейными зависимостями:
σij = λθδij + 2μεij . |
(2.4) |
Кинематическая связь представляется шестью соотношениями, выражающими компоненты тензора деформаций через компоненты вектора перемещений:
εij = |
1 |
( |
∂ui |
+ |
∂u j |
). |
(2.5) |
2 |
∂x j |
∂xi |
|
||||
|
|
|
|
|
К основным уравнениям, определяющим состояние линейно -
упругого тела в его внутренних точках объема V , необходимо присоединить граничные условия на его поверхности S .
