
Механика деформируемого твердого тела
.pdf
Основы физики прочности
Прочностью называется способность элементов конструкций сопротивляться внешним нагрузкам и, таким образом, функционировать в требуемом режиме достаточно продолжительное время.
Разрушение – потеря прочности элементов – выход по какой-либо причине из эксплуатационного режима
По характеру различаются следующие четыре типа разрушения:
9разрушение при упругой деформации;
9разрушение при пластической деформации;
9разрыв (разделение на части);
9изменение свойств материала (металлургическое или химическое).Причина разрушения характеризуется:
9видом нагрузки (установившаяся, неустановившаяся, циклическая);
9длительностью процесса (малая, средняя, продолжительная);
9температурой (низкая, средняя, повышенная).
По месту разрушения могут быть объемные и поверхностные.
К примеру, пластическое течение – это объемное разрушение под действием установившейся нагрузки при комнатной температуре в условиях пластической деформации. Другой пример – многоцикловая усталость – это объемное разрушение при упругой деформации под действием циклической нагрузки в течение продолжительного времени. Малоцикловая усталость отличается от многоцикловой только средней продолжительностью процесса. Коррозия – это поверхностное разрушение под действием установившейся нагрузки при нормальной температуре, вызванное электрохимическим изменением свойств материала.
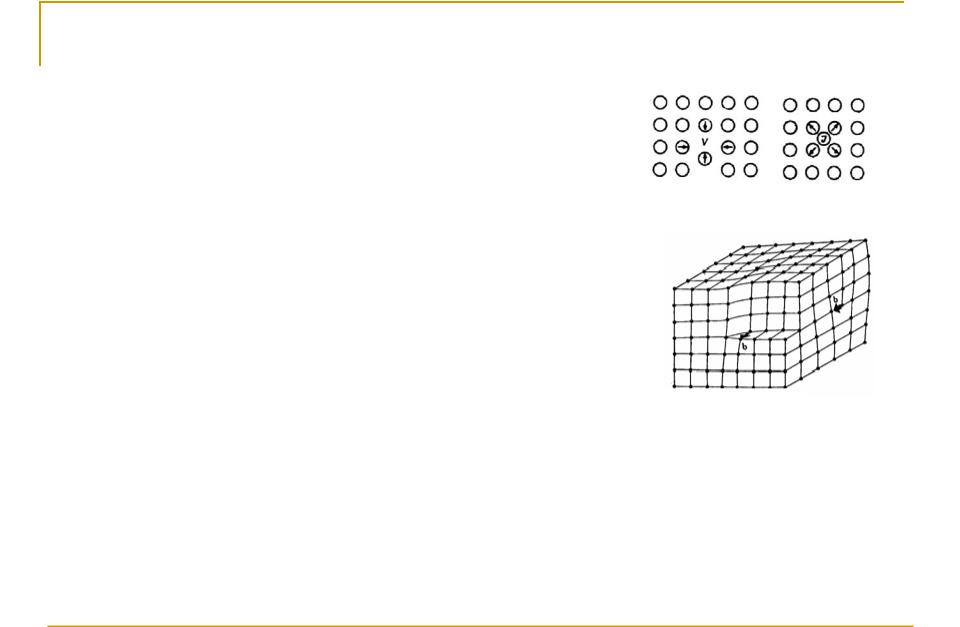
Дефекты кристаллической структуры
Разделяют два типа дефектов – точечные дефекты и дислокации.
К точечным дефектам относятся вакансии, когда в
регулярной атомной решетки по какой либо причине |
|
теряется один из атомов, а также примесные атомы, |
|
когда, наоборот, из-за внешних воздействий появляется |
Точечные дефекты |
лишний атом |
|
|
|
Дислокации бывают краевые и винтовые. |
|
|
|
|
|
Идеальный кристалл и краевая дислокация |
Винтовая дислокация |
Краевые дислокации возникают из-за обрыва атомных плоскостей. Исчезновение части некоторой атомной плоскости приводит к тому, что атомы смежных с нею плоскостей сближаются. Образуется нерегулярная (дефектная) структура. Вектор относительного смещения атомов в физике прочности называется вектором Бюргерса. Для краевой дислокации этот вектор перпендикулярен атомным плоскостям идеальной решетки.
Винтовые дислокации образуются за счет антиплоского сдвига соседних атомных плоскостей. В случае винтовой дислокации вектор Бюргерса параллелен атомным
плоскостям и направлен вдоль линейной цепочки атомов.

Перемещения дислокаций
При деформации кристалла дислокации могут перемещаться. Типичная схема
продвижения дислокации за счет вакансии,
которая образуется на границе кристалла, приведена на рисунке вверху. Соседние дислокации разного знака, у которых
векторы Бюргерса равны по модулю и
противоположны по направлению, могут взаимно уничтожать друг друга (см. рисунок
внизу). В результате происходит |
Перемещение дислокации |
самоупорядочение дефектной структуры с |
|
образованием идеального кристалла. |
|
Может происходить также объединение дислокаций (как краевых, так и винтовых) с последующим их объединением. При объединении одноименных дислокаций с параллельными векторами Бюргерса образуется дислокация с суммарным
вектором. Так происходит зарождение
трещин в твердых деформируемых телах.
Уничтожение дислокаций

Винтовая дислокация
Сингулярное решение уравнений линейной теории упругости, относящееся к случаю винтовой дислокации, строится с помощью уравнений антиплоской деформации, при которой материальные точки тела перемещаются на величину u(x, y) в направлении, перпендикулярном плоскости . Общее решение, описывающее антиплоскую деформацию, строится
спомощью аналитической функции ϕ(z) комплексной переменнойz = x +iy. Формулы для определения u и отличных
τx иτ y , действующих наот нуля касательных напряжений
|
координатных площадках в направлении перемещения, |
|
Труба с разрезом |
||||||||||||
|
имеют вид |
|
|
|
|
|
|
|
|||||||
|
u = |
1 |
Reϕ(z), τx |
−iτ y =ϕ'(z). |
(5.1) |
|
|||||||||
|
|
|
|||||||||||||
|
|
μ |
|
|
|
|
|
|
|
|
|
||||
|
Полагая ϕ(z) = iAln z ≡ iAln | z | −ϑ , где μ |
– модуль сдвига, A – действительная константа, |
|||||||||||||
|
а ϑ = arg z , получимu = −Aϑ μ. При положительном обходе вокруг точки z = 0 |
|
|||||||||||||
|
перемещение получает приращение, равное вектору Бюргерса – относительному |
||||||||||||||
|
смещению берегов разреза вдоль полуоси |
x ≥ 0 |
|
A = −μb (2π) |
. |
||||||||||
|
. Следовательно, |
|
|||||||||||||
|
Справедливо соотношение τx = − |
μb |
|
|
y |
, |
τ y = |
μb |
|
x |
. |
|
|
||
|
2π x2 + y2 |
2π x2 + y2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||
В точке z = 0(на оси дислокации) касательные напряжения имеют неинтегрируемую особенность. В то же время они непрерывны всюду за исключением этой точки. Напряжение, которое действует на окружности радиуса оказывается равным нулю.
Полученное решение описывает напряженно–деформированное состояние бесконечно длинной свободной от напряжений толстостенной трубы, которая была разрезана по образующей и после смещения берегов разреза на величину bсклеена без каких-либо дефектов.

Линейная теория разрушений
Основная задача линейной механики разрушений состоит в изучении поведения трещины в упругом теле, к которому приложена заданная система сил. В зависимости от уровня возникающих при этом напряжений трещина может
находиться в состоянии устойчивого равновесия, а может лавинообразно расти, что
приводит к разделению тела на части.
Рассмотрим сначала несколько точных решений задач теории упругости для бесконечного упругого пространства с линейной трещиной. Первое из них строится на основе комплексного представления (5.1) общего решения задачи об антиплоской
|
деформации. Пусть |
ϕ(z) = −iA z |
= A |
|
|
ϑ |
−i cos |
ϑ |
|
|
||||
|
|
r sin |
|
|
. |
|
||||||||
|
В этом случае перемещение u = A |
r sin ϑ |
|
2 |
|
|
2 |
|
|
|||||
|
|
|
μ |
2 |
|
|
|
|
|
|
|
|
|
|
|
представляет собой разрывную функцию приϑ =π . Решение описывает напряженно– |
|||||||||||||
|
деформированное состояние вокруг линейной трещины, проходящей вдоль полуоси |
x < 0 |
||||||||||||
|
с поперечным сдвигом берегов по закону |
δ = 2u(r,π) |
= 2 A r π |
|
||||||||||
|
Напряжения можно найти из уравнения ϕ'(z) = − |
iA |
|
=τx −iτ y . |
|
|||||||||
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
2 |
|
z |
|
|
|||
Обычно вместо константы A вводится KIII = A π 2 , так называемый коэффициент интенсивности напряжений, с помощью которого решение представляется в форме
π 2 , так называемый коэффициент интенсивности напряжений, с помощью которого решение представляется в форме
|
τx |
= |
KIII |
sin |
ϑ |
, |
τ y = |
KIII |
cos |
ϑ |
, |
u = |
KIII |
2r |
|
|
|
2πr |
2 |
2πr |
2 |
μ |
π |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Критерий Гриффитса
Для трещины в условиях случае антиплоского (поперечного) сдвига силовой критерий выглядит так: KIII = KIIIc , где KIIIc – феноменологический параметр материала, измеряемый экспериментально, который можно найти по справочникам физических величин. Недостаток силового критерия состоит в том, что он не распространяется на более общий случай, когда нагружение представляет собой комбинацию растяжения и одного из двух или двух сдвигов (продольного и поперечного). В связи с этим на практике используется так называемый энергетический критерий
Гриффитса.
Гриффитс выдвинул гипотезу о том, что на образование новой свободной поверхности при росте трещины затрачивается энергия, пропорциональная площади
этой поверхности. Коэффициент пропорциональности, имеющий смысл удельной
энергии, необходимой для образования 1 м2 , обычно обозначается через . Так как
в линейной механике разрушения диссипативными факторами пренебрегают, то затрачиваемая на рост трещины энергия в точности равна упругой энергии, освобождающейся с увеличением ее размеров.
Критерий Гриффитса в плоской задаче можно сформулировать в одной из
следующих форм∂:Uc = 4γ,
где W – упругая энергия, зависящая от длины трещины. Знак “минус” в этом
критерии фигурирует потому, что с ростом трещины энергия убывает, а коэффициент объясняется тем, что общая площадь новой свободной поверхности, учитывая симметрию задачи, равна4 c .
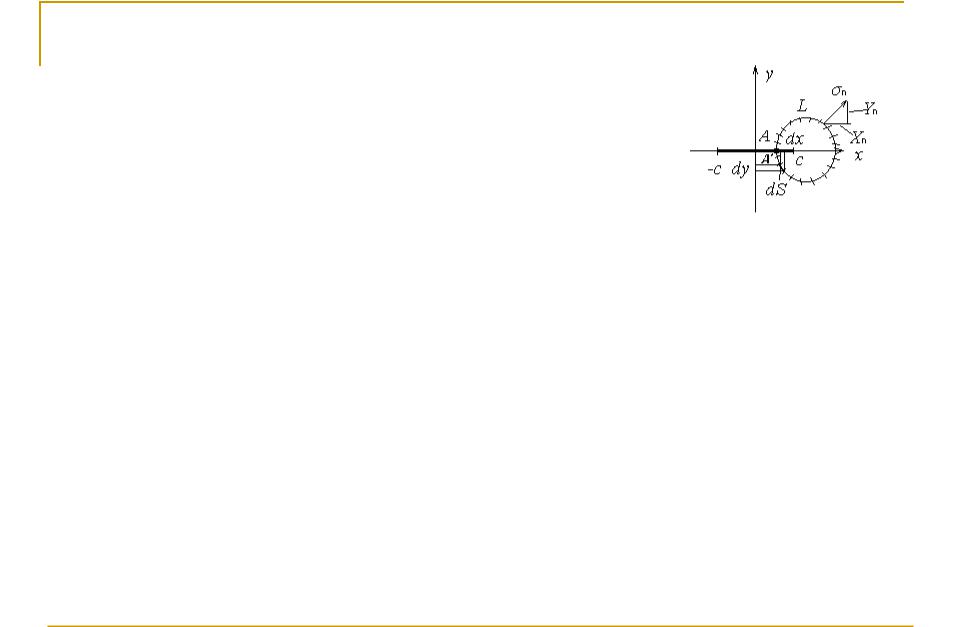
Инвариантный J интеграл
Обобщение энергетического критерия хрупкого разрушения на пластические материалы строится с помощью специального интеграла, который впервые был предложен Черепановым и Райсом.
Интеграл берется по криволинейному контуру без
самопересечений, окружающему вершину трещины. Концы |
Контур интегрирования |
|
контура должны лежать на противоположных берегах |
||
|
||
трещины. |
|
Интеграл вычисляется через заданное поле напряжений и перемещений:
где 2W =σxεx
X n =σ x nx +τxy ny
|
|
|
|
∂u |
|
|
∂u y |
|
|
|
|
X n |
|
x |
− Yn |
|
|
|
|
|
|
|
|
||||||
J = ∫ Wdy − |
∂x |
∂x |
ds |
||||||
L |
|
|
|
|
|
|
|||
+σ yεy +τxyγxy |
– потенциал линейной теории упругости в плоской задаче, |
||||||||
и Yn =τxy nx +σ y ny |
– проекции вектора напряжений, действующего на |
||||||||
площадке с нормальюn . |
A |
∂ |
∂u |
y |
|
|
∂ |
|
∂u |
y |
|
|
||
|
J = ∫ |
W −σx |
ux −τxy |
|
dy + τxy |
ux |
+σ y |
|
dx |
|||||
J–интеграл представим в виде: |
∂x |
∂x |
||||||||||||
AI |
|
∂x |
|
|
∂x |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Важнейшее свойство J–интеграла заключается в его инвариантности, то есть независимости от пути интегрирования. Это свойство выполняется потому, что выражение под знаком интеграла представляет собой полный дифференциал.

Критерий разрушения
Критерий хрупкого разрушения можно представить в терминах J–интеграла как
−J = 2γ
В этой форме критерий разрушения обобщается на случай нелинейно-упругого тела, поскольку в нелинейной теории упругости предполагается существование
потенциала: |
σ |
x |
= |
∂W |
σ |
y |
= |
∂W |
τ |
xy |
= |
∂W |
|||
|
|
|
∂ε |
x |
|
|
∂ε |
y |
|
|
∂γ |
xy |
|||
В этом состоит исключительно важное свойство J–интеграла. Именно в нелинейных
задачах он широко применяется в практических расчетах элементов конструкций с
трещинами на прочность.
Предположим, что в соответствие с нелинейным законом деформирования
напряжение представляет собой степенную функциюα+1 от деформации σ ~ εα с показателем степени α ≤1 . Тогда W ~ σε ~ εα+1 ~ σ α
Выясним, какой порядок роста вблизи вершины трещины имеют напряжения в этом
α+1
случае. Если σ ~ rk , то W ~ rk α
Выбирая в качестве контура интегрирования в J–интеграле окружность радиуса r,
получим |
|
∂ |
∂u |
Ln ∂x +Yn ∂xy ds ~ r α .
Так как значение J – интеграла не зависит от контура интегрирования, то есть от радиуса окружности, то показатель степени здесь должен быть равен нулю, то есть
α+1 = 0 , следовательно k = −α (α +1) .∫ 1+k α+1u
α
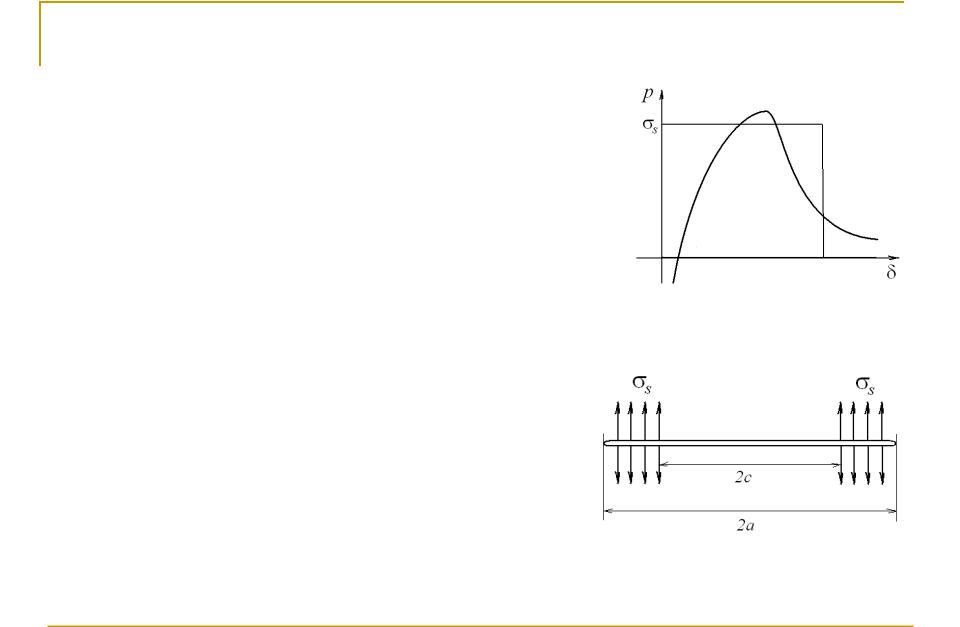
Модель линейной пластической зоны
В общем случае зоны пластической деформации и поле напряжений в окрестности вершины трещины можно определить на основе уравнений теории пластичности. Имеется простой, но, к сожалению, достаточно грубый, аналитический способ учета пластической зоны, который примерно в одно и то же время был предложен с различных точек зрения Панасюком–Леоновым и Дагдейлом.
Панасюк и Леонов рассматривали трещину на
атомном уровне. Они предположили, что
нелинейное взаимодействие происходит только между двумя соседними атомными плоскостями. На рисунке вверху приведена характерная зависимость силы притяжения атомов от межатомного расстояния. Эта зависимость была приближена ступенькой. Возникла модель, изображенная на рисунке внизу. Берега трещины, свободные от напряжений, как бы продолжены линейной пластической зоной, в которой растягивающее напряжение постоянно и равно пределу текучести материала.
Сила межатомного притяжения
Модель пластической зоны

Решение задачи
С помощью формул Колосова–Мусхелишвили можно построить решение более общей
|
задачи для плоскости с разрезом − a ≤ x ≤ a по действительной оси, когда на берегах |
||||||
|
разреза приложено распределенное давлениеσy = −p(x) , а на бесконечности напряжения |
||||||
|
равны нулю. В этом решении коэффициент интенсивности напряжений равен |
|
|||||
|
|
1 |
a |
|
a − xdx |
|
|
|
KI = |
∫ |
p(x) |
|
|
||
|
|
πa |
|
a + x |
|
|
|
|
|
|
−a |
|
|
|
|
|
В задаче с линейной пластической зоной функцию p(x) нужно задать в виде |
|
|||||
|
|
|
|
σ, |
если | x |≤ c, |
|
|
|
p(x) = |
|
|
если c <| x |≤ a. |
|
|
|
|
Тогда после добавления σ0y =σ |
σ −σs , |
|
|
|||
|
получится искомое решение, в котором на продолжениях |
||||||
|
берегов трещины c <| x |≤ a действует растягивающее напряжение σ y |
=σs , а на |
|
||||
|
бесконечности σy =σ . |
|
|
|
|
|
зоназона, |
|
Поле напряжений в окрестности точки x = a , в которой заканчивается |
пластическая |
|||||
|
ограничено. Таким образом: |
c |
|
πσ |
|
||
a= cos 2σs
Приближенная формула для оценки протяженности пластической зоны имеет вид:
c |
|
|
π 2σ 2 |
|
π K e 2 |
|||
|
=1 |
− |
|
d ≡ a −c ≈ |
|
|
I |
|
|
2 |
|
|
|||||
a |
8 |
|
|
|
||||
|
|
8σs |
|
|
σs |
|||
где KIe =σ  πa – коэффициент интенсивности, полученный по сингулярному решению задачи о трещине в рамках теории упругости.
πa – коэффициент интенсивности, полученный по сингулярному решению задачи о трещине в рамках теории упругости.
Так как для идеальной пластичности KI = 0 , то, критерий роста трещины в терминах коэффициента интенсивности напряжений в этом случае неприменим. Такой критерий формулируется в терминах J – интеграла. Критерий разрушения принимает вид:
δc = 2γ 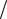 σs
σs
В таком виде он известен как критерий предельного раскрытия трещины.
