
Для студентов / Лекции / (2)ВЕД / (16)Закон збереження імпульсу електромагнітного поля
.doc15. Закон збереження імпульсу електромагнітного поля
Цей розділ буде присвячено
-
виведенню закону збереження імпульсу електромагнітного поля на основі рівнянь Максвела;
-
фізичній інтерпретації усіх величин, які входять до рівняння, що описує просторово-часову зміну імпульсу;
-
аналізу властивостей максвелівського тензору напружень електромагнітного поля і його застосуванням.
Для того, щоб впевнитись в існуванні закону збереження імпульсу і знайти явні вирази для густин імпульсу та потоку імпульсу, будемо виходити, як і в попередньому розділі, з рівнянь Максвела у тій самій формі:
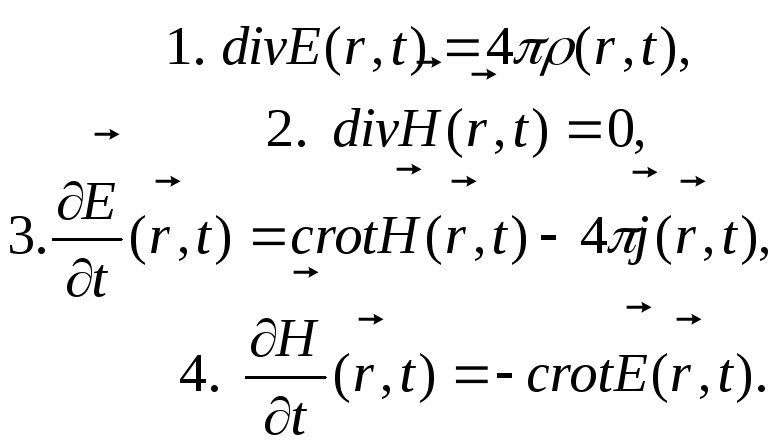 (15.1)
(15.1)
Виконаємо
тепер наступні дії: 1) помножимо з правого
боку обидві частини рівняння (3) векторним
чином на
![]() ,
а рівняння (4) – з лівого боку на
,
а рівняння (4) – з лівого боку на
![]() і 2) просумуємо отримані векторні добутки.
Як наслідок, ми отримаємо наступне
рівняння:
і 2) просумуємо отримані векторні добутки.
Як наслідок, ми отримаємо наступне
рівняння:
![]() (15.2)
(15.2)
де
![]() ,
(15.3)
,
(15.3)
![]() .
(15.4)
.
(15.4)
Тут
комбінація типу
![]() позначає
прямий добуток векторів, тобто, це є
тензор, якому відповідають компоненти
позначає
прямий добуток векторів, тобто, це є
тензор, якому відповідають компоненти
![]() ,
а
,
а
![]() - одиничний тензор, компоненти якого
дорівнюють:
- одиничний тензор, компоненти якого
дорівнюють:
![]() .
Крім того, враховується, що величина
.
Крім того, враховується, що величина
![]() є
вектором, компоненти якого дорівнюють:
є
вектором, компоненти якого дорівнюють:
 .
.
Дійсно, мають місце наступні співвідношення:
![]() ,
(15.5)
,
(15.5)
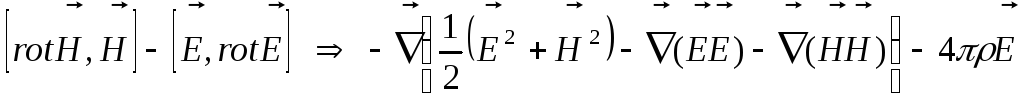 .
(15.6)
.
(15.6)
Щоб переконатись у справедливості (15.6), скористаємось наступним перетворенням:
![]() .
.
Похідна
від скалярного добутку
![]() ,
в якому
,
в якому
![]() слід
вважати постійним вектором, очевидно,
дорівнює половині від
слід
вважати постійним вектором, очевидно,
дорівнює половині від
![]() ,
в якому диференціюються обидва множники
в дужках. Тобто:
,
в якому диференціюються обидва множники
в дужках. Тобто:
![]() .
.
Далі,
![]() .
.
На
останньому кроці ми скористались
означенням скалярного добутку оператора
набла і діади:
![]() (див.
()),
а також першим з рівнянь Максвела.
(див.
()),
а також першим з рівнянь Максвела.
а) Фізичний смисл рівняння (15.2)
Комбінація
![]() ,
яка знаходиться в правій частині
рівняння (15.2), представляє собою силу,
яка діє на всі заряджені частинки в
одиниці об’єму. У згоді з другим законом
Ньютона, часова похідна від імпульсу
частинок, повинна дорівнювати інтегралу
від
,
яка знаходиться в правій частині
рівняння (15.2), представляє собою силу,
яка діє на всі заряджені частинки в
одиниці об’єму. У згоді з другим законом
Ньютона, часова похідна від імпульсу
частинок, повинна дорівнювати інтегралу
від
![]() в межах об’єму
в межах об’єму
![]() системи:
системи:
![]() .
(15.7)
.
(15.7)
Це дозволяє інтегральному аналогу рівняння (15.2) надати вигляд:
![]() ,
(15.8)
,
(15.8)
де
![]() .
Спрямуємо тепер радіус
.
Спрямуємо тепер радіус
![]() поверхні
поверхні
![]() ,
яка охоплює об’єм
,
яка охоплює об’єм
![]() ,
до нескінченості. З причин, які мають
той самий характер, що і по відношенню
до інтеграла
,
до нескінченості. З причин, які мають
той самий характер, що і по відношенню
до інтеграла
 в
попередньому розділі, можна стверджувати,
що
в
попередньому розділі, можна стверджувати,
що
![]() .
.
Як наслідок, ми приходимо до закону збереження:
![]() ,
(15.9)
,
(15.9)
де
![]() .
Звідси випливає, що величина
.
Звідси випливає, що величина
![]() має
смисл сумарного імпульсу електромагнітного
поля, а
має
смисл сумарного імпульсу електромагнітного
поля, а
![]() -
густини імпульсу електромагнітного
поля. До такого ж самого висновку
приводить обчислення фізичних розмірностей
-
густини імпульсу електромагнітного
поля. До такого ж самого висновку
приводить обчислення фізичних розмірностей
![]() і
і
![]() :
[
:
[![]() ]=
]=![]() і
і
![]() .
Це дає нам підстави тлумачити (15.9) як
закон збереження імпульсу електромагнітного
поля.
.
Це дає нам підстави тлумачити (15.9) як
закон збереження імпульсу електромагнітного
поля.
У
згоді з другим законом Ньютона, величина
![]() в
рівнянні (15.8) повинна інтерпретуватись
як сила
в
рівнянні (15.8) повинна інтерпретуватись
як сила
![]() ,
яка діє на поверхню
,
яка діє на поверхню
![]() ,
що обмежує об’єм
,
що обмежує об’єм
![]() .
Компоненти цієї сили дорівнюють:
.
Компоненти цієї сили дорівнюють:
![]() .
.
Звідси випливає, що
-
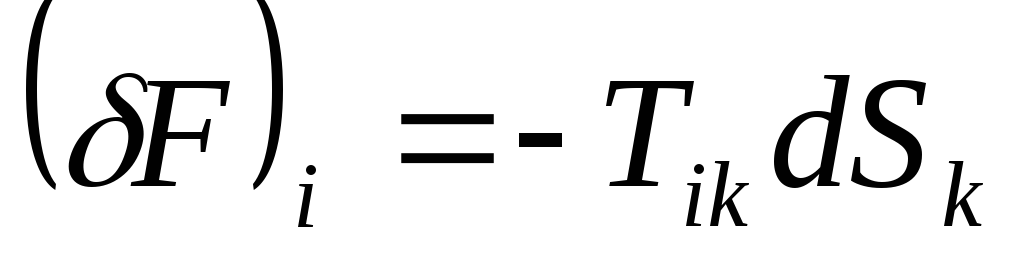 є
є
 та
компонента сили, яка діє на елемент
поверхні
та
компонента сили, яка діє на елемент
поверхні
 ,
просторова орієнтація якого задається
ортом
,
просторова орієнтація якого задається
ортом
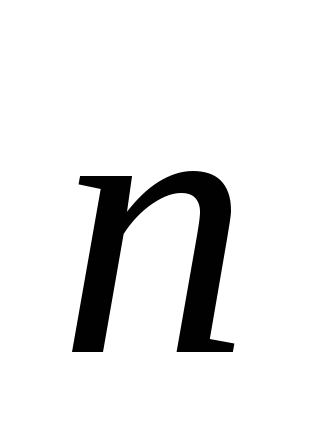 :
:
 ;
; -
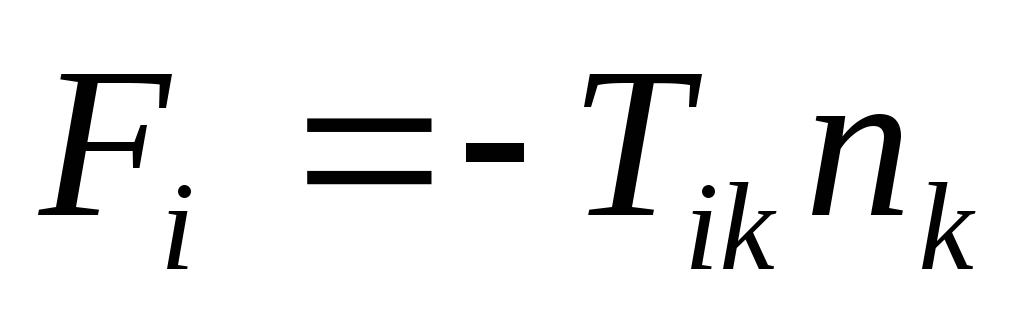 є сила,
яка діє на одиничну площадку, просторова
орієнтація якої задається ортом
є сила,
яка діє на одиничну площадку, просторова
орієнтація якої задається ортом
 ;
; -
 є сила,
яка діє на одиничну площадку,
перпендикулярну до вісі, якій відповідає
індекс
є сила,
яка діє на одиничну площадку,
перпендикулярну до вісі, якій відповідає
індекс
 (в цьому випадку
(в цьому випадку
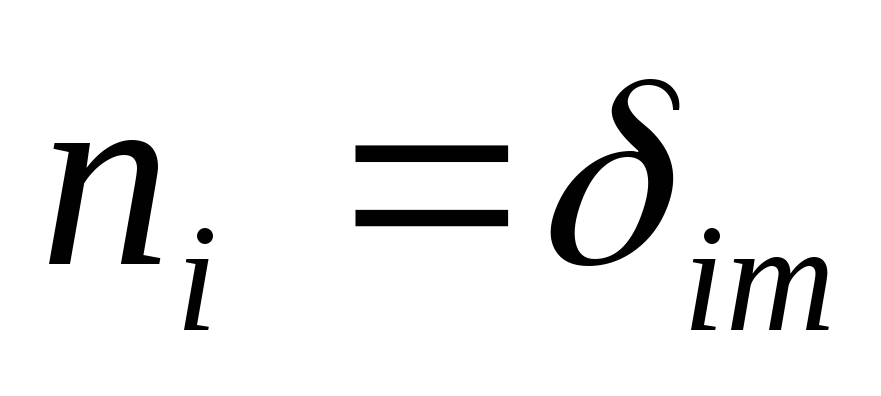 ).
).
У згоді
з цим, тензор
![]() прийнято
називати тензором напружень
електромагнітного поля, або максвелівським
тензором напружень електромагнітного
поля. Оскільки тензор напружень є
симетричним:
прийнято
називати тензором напружень
електромагнітного поля, або максвелівським
тензором напружень електромагнітного
поля. Оскільки тензор напружень є
симетричним:
![]() ,
то можна також сказати, що
,
то можна також сказати, що
![]() є
є
![]() а
компонента сили, яка діє на одиничну
площадку, перпендикулярну до
а
компонента сили, яка діє на одиничну
площадку, перпендикулярну до
![]() ї
вісі.
ї
вісі.
Оскільки
![]() ,
то величину
,
то величину
![]() або
або
![]() ,
(15.10)
,
(15.10)
можна тлумачити як густину об’ємних сил, які діють на систему зарядів і токів з боку електромагнітного поля.
Якщо
в певному об’ємі
![]() заряди і токи є відсутніми, з (15.2) випливає,
що електромагнітне поле задовольняє
рівнянню:
заряди і токи є відсутніми, з (15.2) випливає,
що електромагнітне поле задовольняє
рівнянню:
![]() ,
(15.11)
,
(15.11)
яке є
цілком подібним до тих, що описують
закони збереження заряду та енергії
(див. попередній розділ (15)). Інтегруючи
(15.7) в межах об’єму
![]() ,
знаходимо:
,
знаходимо:
![]() .
(15.12)
.
(15.12)
Звідси
випливає, що тензор
![]() може
також тлумачитись як густина потоку
імпульсу через поверхню, яка обмежує
об’єм
може
також тлумачитись як густина потоку
імпульсу через поверхню, яка обмежує
об’єм
![]() .
Діючи у такий самий спосіб, як і при
опису сил, діючих на поверхню
.
Діючи у такий самий спосіб, як і при
опису сил, діючих на поверхню
![]() ,
можна стверджувати, що
,
можна стверджувати, що
-
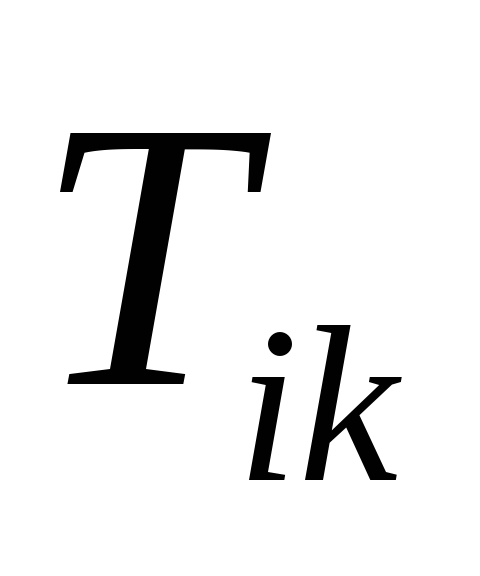 є
є
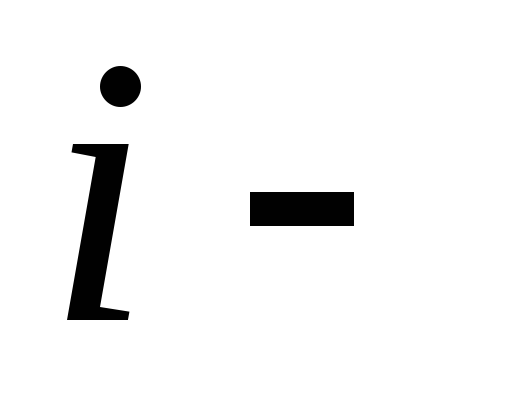 та
компонента густини імпульсу, що протікає
через одиничну площадку, перпендикулярну
вісі
та
компонента густини імпульсу, що протікає
через одиничну площадку, перпендикулярну
вісі
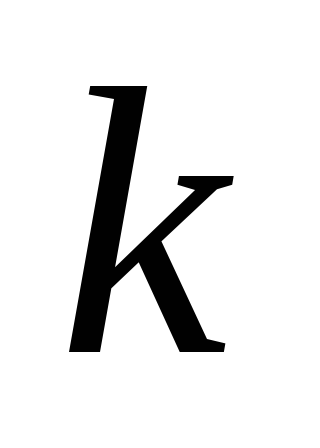 .
Завдяки його симетрії, можна також
стверджувати, що
.
Завдяки його симетрії, можна також
стверджувати, що
 є
є
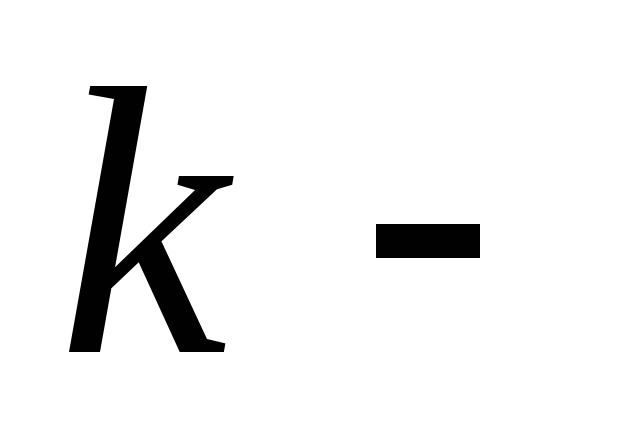 та
компонента густини імпульсу, що протікає
через одиничну площадку, перпендикулярну
вісі
та
компонента густини імпульсу, що протікає
через одиничну площадку, перпендикулярну
вісі
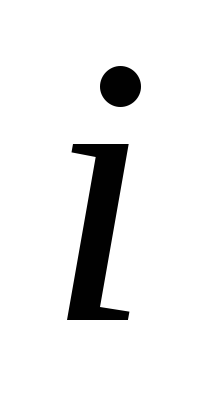 .
.
