§ 21. Энергия магнитной линии (единичной трубки магнитной

индукции).

В начале настоящего курса говорилось, что мы мыслим магнит­ный поток состоящим из магнитных линий, т. е. из ряда элементар­ных (единичных) трубок магнитной индукции. Отсюда следует, что н полную энергию в объеме, занятом магнитным потокам (при условии =const):

можно представить распределенной между отдельными магнитными линиями, т. е. единичными трубками. Подсчитаем энергию, прихо­дящуюся на долю единичной трубки магнитной индукции, т. е. трубки, для которой

Ф₁= Hs=1,

иначе говоря, энергию одной магнитной линии.

Элемент объема трубки dv=sdl содержит магнитную энергию:

Следовательно, во всей трубке заключается энергия:

Так как Hs=l, то

100

что, по § 17, приводит к чрезвычайно простому соотношению:

Итак, энергия, отнесенная к единице магнитного потока (одной магнитной линия), выражается половиною силы тока, сцепляющегося с данным магнитным потоком.

Таким образом, например, при I=10 ампер энергия единичной трубки (одной магнитной линии):

и т. д.

Подсчитаем, пользуясь только-что выведенным соотношением, энергию потока самоиндукции, связанного с некоторым током i. Величина этого потока, как известно, равна:

Ф_s=Li,

где L—коэффициент самоиндукция, представляющий собою полное число сцеплений реально существующего потока самоиндукции с данным контуром тока, сила которого при этом принимается рав­ной единице (см. § 99).

Рассмотрим самый общий случай, когда мы имеем сколь угодно сложный контур тока. Допустим, что в случае, когда, сила тока в контуре равна единице, k₁ магнитных линий реально существую­щего потока сцепляются с n₁ витками; k₂ магнитных линий сцеп­ляются с n₂ витками; k₃ магнитных линий сцепляются с n₃ витками и т. д. Если же сила тока равна i, то пропорционально силе тока изменяется и поток самоиндукции, т. е. при этом:

Принимая во внимание данное выше соотношение (18) для энер­гии, отнесенной к одной магнитной линии, получаем:

А все магнитные линии потока самоиндукции являются носите­лями запаса анергии:

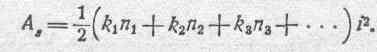
101

Согласно определению, имеем:

Следовательно, окончательно получаем:

A_s=¹/₂Li².

Обратим внимание на сходство этого выражения с выражением кинетической энергии механической системы: ¹/₂mv²; смысл этой ана­логии мы уясним в дальнейших частях курса (см. § 28 и главу VII).

На основании всего предыдущего ясно, что, распространяя ин­тегрирование на весь объем, занятый потоком самоиндукции, мы можем написать:

§ 22. Тяжение магнитных линий.

При дальнейшем изучении свойств магнитного потока мы оста­новимся на явлении тяжения магнитных линий. Совершенно есте­ственно представлять себе все явления, происходящие в магнитном поле, как следствие особых свойств магнитного потока в целом и составляющих его единичных трубок магнитной индукции в частно­сти. Фарадей, создавший представление о магнитном поле как о совокупности физически существующих магнитных линий, рассма­тривал все явления, происходящие в магнитном поле, именно как результат проявления свойств этих элементов магнитного потока. По Фарадею, магнитные линии ведут себя как упругие нити, стремящиеся сократиться. Это проявляется, например, в обнаружи­ваемом магнитными линиями стремлении сблизить элементы маг­нитной цепи. Вообще, во всех случаях, когда в результате суще­ствования магнитного поля возникают механические силы, их можно отнести за счет стремления магнитных линий к сокращению.

Максвелл, подвергший тщательному математическому обсле­дованию все свойства магнитного потока, показал путем анализа и в полном согласии с воззрениями Фарадея, что в магнитном поле должны возникать механические напряжения, которые должны производить соответствующие механические же воздействия на все материальные тела, внесенные в поле. Для случая неоднородной анизотропной среды выражение для этих сил получает сложный вид. Мы ограничимся рассмотрением простейшего случая однород­ной изотропной среды.

Представим себе (рис. 55) два разноименных полюса и нарисуем картину распределения магнитных линий в этом случае.

Если щель между полюсами достаточно узка, то в центральной части ее поле можно считать однородным. По бокам же однородность поля нару-

102

шается. Для того, чтобы это обстоятельство не затрудняло рас­смотрения вопроса, вырежем среднюю цилиндрическую часть север­ного полюса, получив таким образом вокруг нее „охранное кольцо", которое даст нам возможность в наших расчетах принимать во вни­мание лишь среднюю часть пространства между полюсами, где поле является однородным. Вырезанная часть представится в виде цилиндра с поперечным сечением s.

В силу своей упругости, магнитные линии будут стягивать полюсы, и вырезанный элемент магнита будет находиться под действием сил тяжения. Постараемся определить величину силы тя­жения, действующей на пло­щадь s. Расчет будем вести, исходя из выражения для энер­гии магнитного потока и прин­ципа сохранения энергии.

Обозначим через f' силу тяжения, действующую на единицу поверхности, а че­рез f — силу, действующую на всю площадку s. Тогда

f=f's.

Для расчета предполо­жим, что центральная ци­линдрическая часть под действием сил тяжения несколько сместилась, причем величину этого элементарно малого смещения обозначим через dl (положение сме­стившегося цилиндра показано на рис. 55 пунктиром). Такое смещение вызовет соответствующее изменение количества энер­гии, запасенной в магнитном поле, так как работа перемещения за отсутствием других источников энергии может быть произведена лишь за счет энергии магнитного потока. Действительно, объем поля в пространстве между магнитами стал меньше, и количество энергии, запасенной в поле, должно соответственно уменьшиться. Полный интересующий нас объем, занимаемый полем между магнитами, выражается произведением ls, где l есть расстояние между полюсами. Считая запас энергии на единицу объема равным (17)

и пренебрегая бесконечно малыми высших порядков, получим, что, при перемещении цилиндра на элемент dl, в механическую работу превратится часть энергии магнитного поля, равная

103

С другой стороны, эта же работа равна

Следовательно, на основании закона сохранения энергии, можем написать:

или, сокращая на sdl, получаем в динах на кв. сантиметр:

т. е. сила тяжения магнитных линий, рассчитанная на единицу поверх­ности, нормальной к поверхности потока, численно равна количе­ству энергии магнитного поля, рассчитанному на единицу объема.

Мы рассчитывали величину силы тяжения, действующей на еди­ницу поверхности полюса, к которому, так сказать, „присосались" магнитные линии. Исходя из положения, что магнитные линии ве­дут себя как упругие нити, естественно заключить — как это сде­лал Фарадей и математически обосновал Максвелл,—что та­кая же сила тяжения имеет место в любом поперечном сечении потока. Необходимо иметь в виду, что полученное выражение (19) пригодно лишь для однородной и изотропной среды, и =const. При несоблюдении этих условий характер явления в основном остается тем же, но математическая формулировка соответствующих зависимостей значительно усложняется.

Пользуясь равенством H=B, мы можем преобразовать полу­ченное выражение следующим образом:

*

Обычно мы наблюдаем механические проявления магнитного поля в воздухе, т.е. при =1. В этом случае f' численно равно:

104

¹) В этой и предыдущих формулах может обратить на себя внимание парадо­ксальный, на первый взгляд, факт, именно, что выражения для силы и для энергии как бы совпадают между собой. Кажущаяся парадоксальность исчезнет, если мы вспомним, что в формулах (19) и (17) фигурируют сила, рассчитанная на единицу поверхности, и энергия, рассчитанная на единицу объема. Не трудно убедиться, что при этих условиях размерности той и другой величины совпадают: