ТК-теор2012
.pdf
31
Типовая задача 11 (рис. 44-45): Построить гори-
зонтальный, фронтальный и профильный разрезы детали (рис. 38), имеющей гладкое и ступенчатое отверстия, а
также ребро жёсткости. Рассекаем деталь горизонтальной плоскостью уровня А-А, проходящей через ось гладкого
отверстия и размещаем горизонтальный разрез на месте вида сверху (рис. 45). Рассекаем деталь профильной плоскостью уровня Б-Б, проходящей через ось ступенчатого отверстия и размещаем профильный разрез на месте вида
слева. Рассекаем деталь фронтальной плоскостью уровня, Рис. 44 совпадающей с плоскостью симметрии детали (без обо-
значения), получим фронтальный разрез на месте главного вида. Секущая плоскость проходит вдоль ребра жёсткости, поэтому оно не штрихуется.
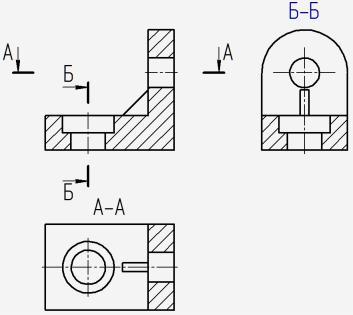Рис. 45
Сечение — это ортогональная проекция фигуры, получающейся в секущей плоскости. Сечения тел представляют собой плоские фигуры, а сечения поверхностей – линии. В сечении изображается только то, что располагается в секущей плоскости. Сечение – это часть разреза. Для сравнения на рис. 46 изображено сечение, выполненное той же секущей плоскостью А-А, что и разрез на рис. 41. Сечения подразделяются на вынесенные (рис. 46, 47) и наложенные (рис. 48). Контур вынесенного сечения, а также сечения, входящего в состав разреза изображают сплошными основными линиями, а контур наложенного сечения — сплошными тонкими линиями (рис 48). Оформление вынесенных сечений на чертеже такое же, как и разрезов.
|
. |
|
Рис. 46 |
Рис. 47 |
Рис. 48 |
31
32
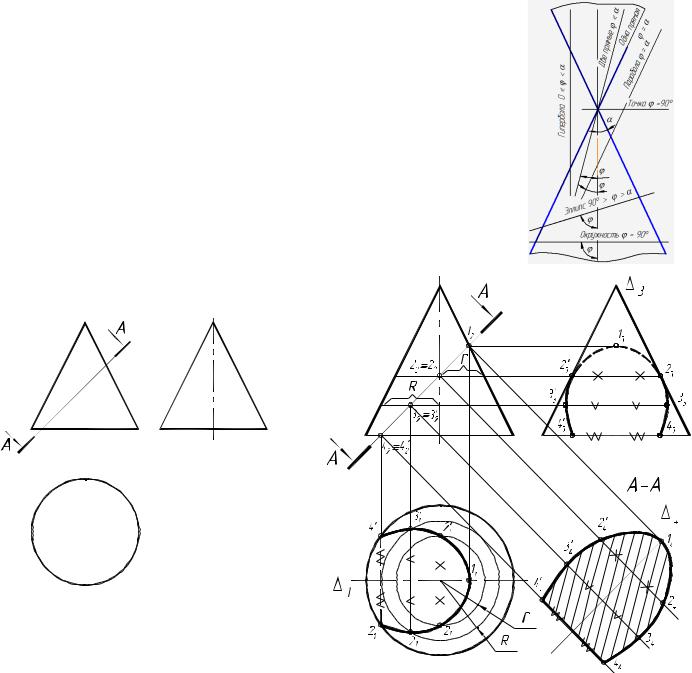
Линии конических сечений – это линии, образующиеся при пересечении конуса вращения плоскостями (коники). В зависимости от положения секущей плоскости, угла её наклона к оси конуса и угла конуса линиями сечения могут быть (рис. 49):
окружность – плоскость перпендикулярна оси конуса, эллипс – плоскость пересекает все образующие и > , парабола – плоскость параллельна одной из образующих, гипербола – плоскость параллельна оси конуса,
две пересекающиеся прямые – плоскость проходит через вершину конуса и < ,
одна прямая – плоскость касается образующей конуса, точка - плоскость проходит через вершину конуса и =90 .
. |
Рис. 49 |
Типовая задача 12 (рис. 50): Построить горизонталь- |
|
ную и профильную проекции сечения конуса плоскостью |
|
А-А. Определить натуральную вели- |
|
чину сечения. |
|
Рис. 50 |
Рис. 51 |
1.По собирательному свойству проеци- |
|
рующей плоскости (см. с. 14) |
искомая ли- |
ния сечения совпадает с её фронтальным |
|
следом на участке перекрытия его очерком конуса (рис. 51). На вырожденной проекции сече- |
|
ния задаём точки 12 ; 22 ; 2'2 ; 32 ; 3'2 ; 42 ; 4'2 . Первая точка одинарная, т. к. лежит на очерковой |
|
образующей конуса; остальные - двойные. |
|
2.На поверхности конуса через эти точки проводим окружности r и R, которые на фронтальной плоскости проекций вырождаются в прямые. Строим горизонтальные проекции окружностей. Через заданные проекции точек, проведя вертикальные линии связи до пересечения с окружностями, получим их горизонтальные проекции. Соединив полученные точки, имеем горизонтальную проекцию сечения. Определяем видимость линии сечения.
3.Профильную проекцию сечения строим с помощью базовой плоскости ‖П2 . Измеряем на горизонтальной проекции удаления точек сечения от базовой линии 1 (отмечены галочками и крестиками) и откладываем их на профильной плоскости проекций от базовой линии 3 .
4.Натуральную величину сечения получим, проецируя сечение на дополнительную пл. П4 , параллельную плоскости сечения и перпендикулярную пл. П2 . На чертеже задаём базовую ли-
нию 4 параллельную линии сечения А-А, проводим линии связи перпендикулярные базовой линии 4 и строим дополнительную проекцию сечения на плоскость П4 точно также, как, например, профильную проекцию. Построение сечений см. также в [14].
32
33
ПОВЕРХНОСТИ |
|
Поверхность - это двухпараметрическое мно- |
|
жество точек. Поверхность можно представить как |
|
общую часть двух смежных пространств. Порядок гра- |
|
фической поверхности определяется по числу точек |
|
пересечения её прямой линией. |
|
В начертательной геометрии используется ки- |
|
нематический принцип представления поверхности как |
|
совокупности всех последовательных положений неко- |
|
торой перемещающейся в пространстве линии li , на- |
|
зываемой образующей (рис. 52). Траектория m, по ко- |
|
торой перемещается образующая линия, называется |
Рис. 52 |
направляющей линией. Образующие и направляющие линии одной поверхности можно менять местами. В качестве направляющей линии часто задают линию, по которой данная поверхность пересекает пл. П1 .
Способы задания поверхностей на чертеже
Поверхность на комплексном чертеже может быть задана: определителем поверхности, каркасом, условными проекциями. Поверхность считается заданной, если по известной проекции точки, принадлежащей данной поверхности, можно построить вторую её проекцию.
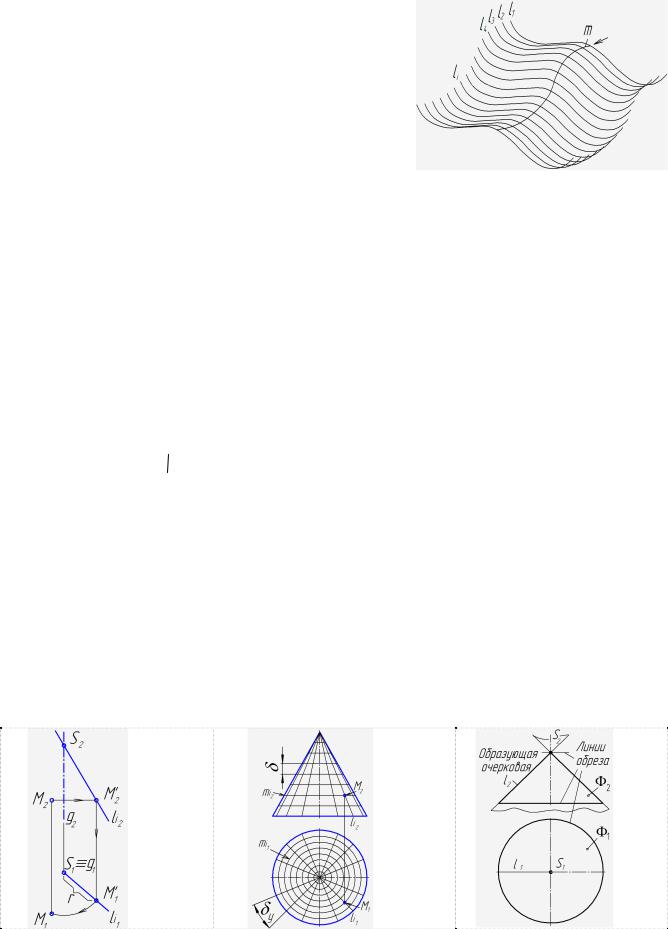
Определитель поверхности – задаваемая совокупность независимых условий, однозначно определяющих поверхность. Определитель состоит из двух частей: геометрической и алгоритмической. В геометрическую часть входит совокупность геометрических фигур.
В алгоритмическую часть — сведения о характере образующей и законе образования поверхности. Первую часть заключают в круглые скобки, вторую — в квадратные. Например: определитель конической поверхности вращения имеет вид (рис. 53):
(l, g, S); [li ∩g=S, li g], где: S вершина конуса, l образующая, g ось конуса.
С помощью этого определителя по заданной фронтальной проекции точки М(М2 ) , построена её горизонтальная проекция М1 . Графическая лаконичность определителя поверхности не отличается наглядностью.
Каркас – упорядоченное множество линий, принадлежащих поверхности. Он может быть простым - состоять из линий одного семейства (рис. 52), или сетчатым – из линий двух семейств (рис. 54). Линии, составляющие каркас, это последовательные положения образующей при её движении по направляющей, а также линии сечения поверхности пучками плоскостей: параллельных или проходящих через ось (для тел вращения). Например, сетчатый каркас конической поверхности вращения составляют два семейства линий (см. рис. 54):
1) li – образующие – прямые, проходящие через вершину S; 2) mi - окружности переменного радиуса с центром на оси конической поверхности. Плотность каркаса определяется дискретами: линейным или угловым у промежутками между смежными линиями каркаса. Каркасный способ отличается хорошей наглядностью, позволяет легко строить недостающие проекции точек, расположенных на его линиях, но достаточно трудоёмок в исполнении.
Рис. 53 |
Рис. 54 |
Рис. 55 |
33
34
Условные проекции поверхности – проекции очерка отсека (части) поверхности, включающего в себя, кроме проекций линий контура (очертания), также проекции линий обреза (рис. 55). Очертания проекций поверхности изображают с отсечёнными частями, что позволяет увеличить масштаб её изображения и чёткость чертежа. Этот способ, ввиду простоты и наглядности задания поверхностей, применяется наиболее часто (рис. 66).
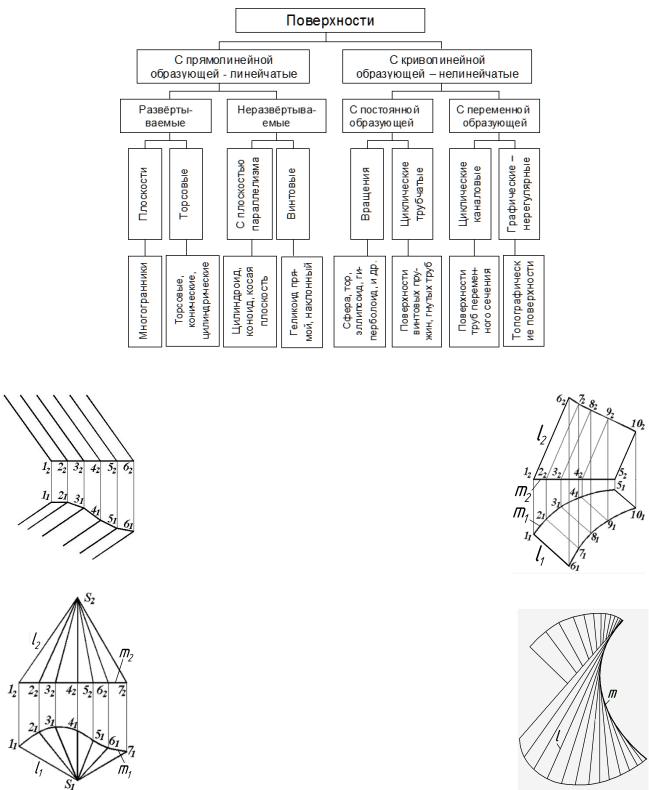
Поверхности различаются по: форме образующей, закону её движения, признаку развёртываемости, закону изменения формы образующей, закону образования поверхности и др. признакам. Любую поверхность можно получить разными способами. На практике выбирают самый простой.
Поверхности линейчатые развертываемые: гранные, цилиндрические, конические, торсовые. Направляющая линия – прямая.
|
Гранная поверхность - это совокупность |
|
|
плоскостей. Такую поверхность имеют все мно- |
|
|
гогранники. На рис. 56 представлена гранная |
|
|
призматическая поверхность. |
|
|
Цилиндрическая поверхность (рис. 57) обра- |
|
|
зуется параллельным движением прямой линии l, |
|
|
проходящей последовательно через все точки |
|
|
некоторой кривой направляющей линии m. |
|
|
Коническая поверхность (рис. 58) |
|
Рис. 56 |
образуется прямой линией l, проходящей после- |
|
довательно через все точки кривой направляю- |
Рис. 57 |
|
|
щей линии m и через неподвижную точку, назы- |
|
|
|
|
|
ваемой вершиной конической поверхности S. |
|
|
Торс (рис. 59) образуется движением прямо- |
|
|
линейной образующей l, касающейся во всех сво- |
|
|
их положениях некоторой пространственной |
|
|
кривой m, называемой ребром возврата, которое |
|
|
делит торс на две полости. |
|
|
Коническую и цилиндрическую поверхности |
|
|
можно рассматривать как частные случаи по- |
|
|
верхности торса, когда её ребро возврата вы- |
|
|
рождается в точку (конечную или бесконечно |
|
Рис. 58 |
удалённую). |
Рис. 59 |
|
||
|
34 |
|
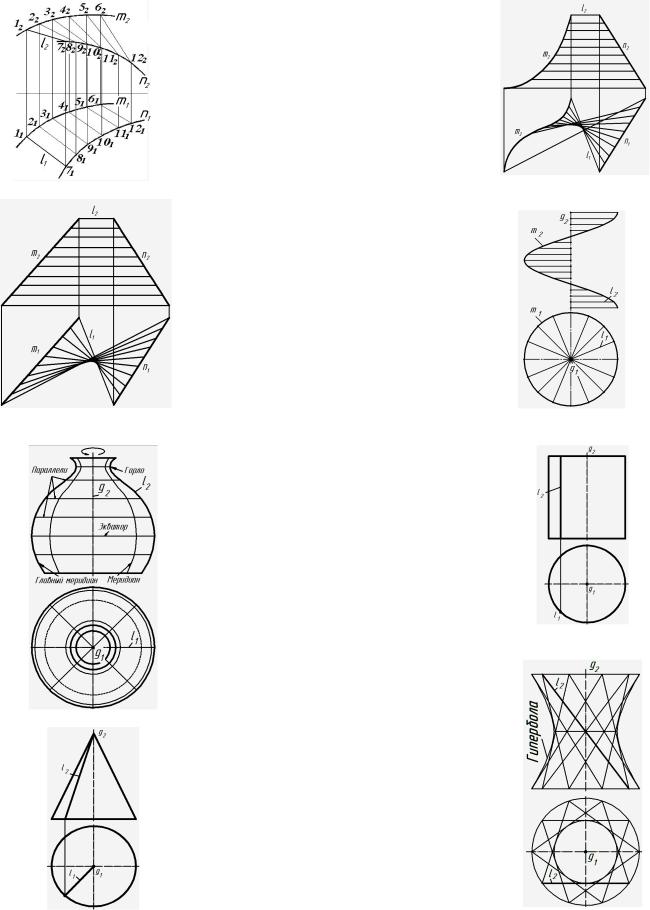
35
Поверхности линейчатые неразвёртываемые
Поверхности с плоскостью параллелизма (Каталана): цилиндроиды, коноиды, косая плоскость.
|
|
Эти поверхности образуются при пе- |
|
|
|
|
|
|
ремещении прямой линии l, во всех своих |
|
|
|
|
|
|
положениях сохраняющей параллельность |
|
|
|
|
|
|
некоторой заданной плоскости (плоско- |
|
|
|
|
|
|
сти параллелизма), и пересекающей две |
|
|
|
|
|
|
направляющие скрещивающиеся линии m и |
|
|
|
|
|
|
n. |
|
|
|
|
|
|
Получаемая поверхность с плоско- |
|
|
|
|
|
|
стью параллелизма определяется конфи- |
|
|
|
|
|
|
гурацией двух направляющих скрещи- |
|
|
|
|
Рис. 60 |
|
вающихся линий. Если они обе (m и n) |
Рис. |
61 |
|
|
|
кривые линии, то образующаяся поверх- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ность - цилиндроид (рис 60), если одна |
|
|
|
|
|
|
из них кривая, а другая прямая, то – |
|
|
|
|
|
|
коноид (рис 61), а если обе направляющие |
|
|
|
|
|
|
– прямые линии, то – косая плоскость |
|
|
|
|
|
|
или гиперболический параболоид (рис. |
|
|
|
|
|
62). |
|
|
|
|
|
|
|
Коноид, у которого одна направ- |
|
|
|
|
|
|
ляющая - винтовая линия (гелиса) m, а |
|
|
|
|
|
|
вторая направляющая – её ось g, назы- |
|
|
|
|
|
|
вается винтовым. Другое название этой |
|
|
|
|
|
|
винтовой поверхности – прямой гелико- |
|
|
|
|
Рис. 62 |
|
ид (рис 63). |
Рис. |
63 |
|
|
|
|
Поверхности вращения |
|
|
|
|
|
|
образуются в общем случае вращением |
|
|
|
|
|
|
некоторой образующей l вокруг оси g |
|
|
|
|
|
|
(рис. 64). Все точки образующей описы- |
|
|
|
|
|
|
вают в пространстве окружности с цен- |
|
|
|
|
|
|
тром на оси вращения – параллели. Наи- |
|
|
|
|
|
|
большая и наименьшая параллель назы- |
|
|
|
|
|
|
ваются соответственно экватор и гор- |
|
|
|
|
|
|
ло. Плоскости, проходящие через ось по- |
|
|
|
|
|
|
верхности вращения, называются ме- |
|
|
|
|
|
|
ридиональными, а линии, по которым они |
|
|
|
|
|
|
пересекают поверхность – меридианами. |
Рис. |
65 |
|
|
|
|
Меридиональная плоскость, параллельная |
|
|
|
|
|
|
плоскости проекций, даёт в сечении |
|
|
|
|
|
|
главный меридиан. |
|
|
|
|
|
|
Прямолинейная образующая l, в за- |
|
|
|
|
Рис. 64 |
|
висимости от её положения относи- |
|
|
|
|
|
|
тельно оси вращения g, может образо- |
|
|
|
|
|
|
вывать линейчатые поверхности: |
|
|
|
|
|
|
1) цилиндрическую если l g (рис. 65); |
|
|
|
|
|
|
2) коническую если l∩g (рис.66); |
|
|
|
|
|
|
3) однополостного гиперболоида если |
|
|
|
|
|
|
l g (рис. 67). Эта поверхность может |
|
|
|
|
|
|
быть также образована вращением ги- |
|
|
|
|
|
|
перболы вокруг мнимой оси g. Эта по- |
|
|
|
|
|
|
верхность, в отличии от цилиндрической |
Рис. |
67 |
|
|
Рис. 66 |
|
и конической, - неразвёртываемая. |
|
|||
35
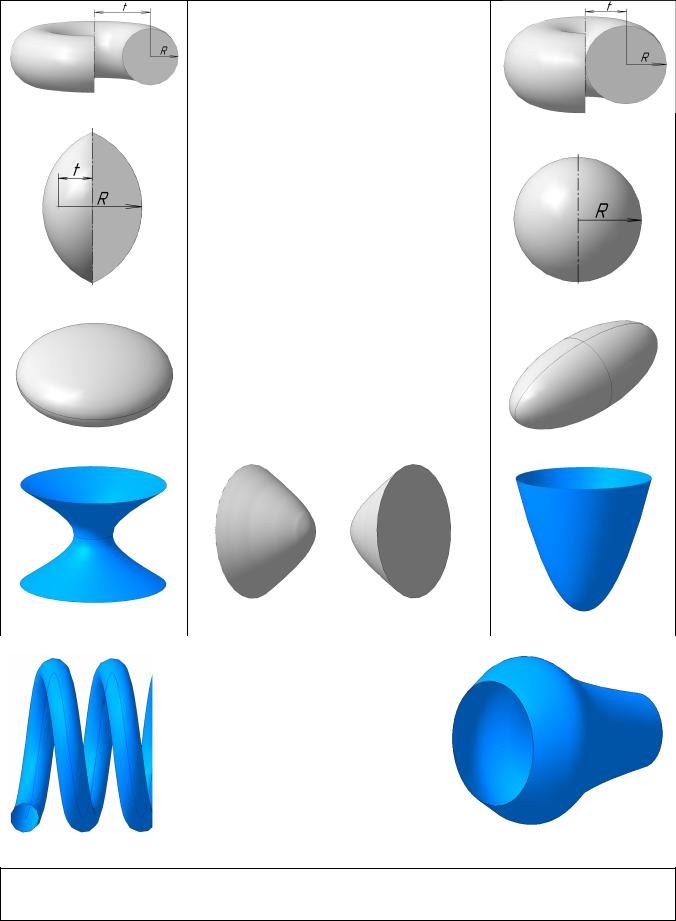
36
Рис. 68
Рис. 70
Рис. 72
В качестве криволинейных образующих
для получения поверхностей вращения часто используют кривые 2-го порядка: окружность, эллипс, параболу, гиперболу и др. Окружность и её части, в зависимости от расположения оси вращения, образуют следующие поверхности:
Тор открытый (кольцо) при R<t (рис. 68).
Тор закрытый замкнутый при R=t (рис.69).
Тор закрытый самопересекающийся при
R>t (рис. 70).
Сфера при t=0 (рис. 71).
Поверхности, образованные вращением кривых 2-го порядка вокруг их осей симметрии: эллипсоид сжатый (рис. 72), эллипсоид вытянутый (рис. 73), гиперболоид однополостный (рис. 74), гиперболоид двуполостный (рис. 75) параболоид
(рис. 76).
Рис. 69
Рис. 71
Рис. 73
Рис. 74 |
Рис. 75 |
Рис. 76 |
|
||
|
|
|
|
Циклические поверхности |
|
|
образуются перемещением ок- |
|
|
ружности, центр которой пере- |
|
|
мещается по заданной направ- |
|
|
ляющей линии. Если образующая |
|
|
окружность постоянного радиу- |
|
|
са, то формируются трубчатые |
|
|
циклические поверхности (рис. |
|
|
77), если окружности перемен- |
|
|
ного радиуса, то – каналовые |
|
|
циклические поверхности (рис. |
|
Рис. 77 |
78). |
Рис. 78 |
Топографические поверхности
- поверхности не подчиняющиеся какому-либо геометрическому закону. Это поверхности земной коры, корпуса судов, обшивка самолётов, автомобилей. Они задаются на чертежах с помощью простого каркаса (географическая карта) или сетчатого каркаса (корпуса судов).
36
37
|
Типовая задача 13 (рис. 79): По заданной проек- |
|
||
|
ции точки М(М2 ) построить её другую проек- |
|
||
|
цию — М1. Используется признак: Точка принадлежит |
|
||
|
поверхности, если она принадлежит линии, принадле- |
|
||
|
жащей поверхности. |
Алгоритм: |
|
|
|
1) Анализ поверхности; 2) Через заданную проекцию точки |
|
||
|
провести вспомогательную для построения линию (обра- |
|
||
|
зующую, направляющую (окружность для тел вращения)); |
|
||
|
3) Построить другую проекцию вспомогательной линии; |
|
||
|
4) Проведя линию связи через заданную проекцию точки |
|
||
|
до пересечения с проекцией вспомогательной линии, най- |
|
||
|
ти искомую проекцию точки. |
|
|
|
Рис. 79 |
Алгоритм подходит для построения точек на всех |
|
||
поверхностях, в том числе и на плоскости. |
Рис. 80 |
|||
|
||||
Решение (рис. 80 ): 1) Поверхность Ф является конической вращения. Для привязки заданной точки к поверхности используем образующую или окружность; 2) Проводим через точку М2 образующую l2 или окружность m2. 3) Строим горизонтальную проекцию образующей l1 или окружности m1. 4) От точки М2 ,проведя вертикальную линию связи до пересечения с горизонтальной проекцией образующей или окружности, получаем горизонтальную проекцию точки М1 Как видно из рис. 80, оба решения совпали.
ПОЗИЦИОННЫЕ ЗАДАЧИ
- это задачи на определение взаимного положения геометрических объектов. Их 3 группы:
1.Задачи на взаимный порядок (размещение объектов в ограниченном пространстве (в ракетах, подводных лодках), определение видимости конкурирующих элементов).
2.Задачи на взаимную принадлежность (точек и линий плоскости или поверхности).
3.Главные позиционные задачи (ГПЗ) – задачи на построение точек пересечения линий с поверхностями или линий пересечения поверхностей.
Взависимости от вида объектов и их положения различают 3 случая ГПЗ.
1-й случай (ГПЗ-1) – оба пересекающихся объекта занимают проецирующее положение ( , ). Возможны 2 варианта: ГПЗ-1а – объекты перпендикулярны одной и той же пл. проекций; ГПЗ-1б - объекты перпендикулярны разным плоскостям проекций;
2-й случай (ГПЗ-2) – один из 2-х пересекающихся объектов занимает проецирующее положение ( , ).
3-й случай (ГПЗ-3) – оба пересекающихся объекта не занимают проецирующее положение (общий случай решения позиционных задач) ( , ).
Проецирующие объекты
- это объекты, перпендикулярные к одной из плоскостей проекций и одноимённые ей.
Существует 4 вида проецирующих объектов:
37
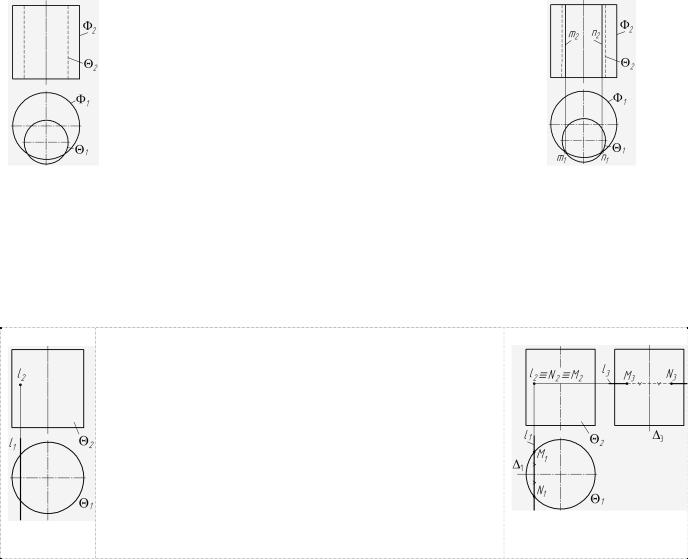
38
Свойства проецирующих объектов:
1.Одна из проекций этих объектов вырождается в точку или линию.
2.Одна из проекций точек или линий, принадлежащих проецирующему объекту, совпадает с его вырожденной проекцией.
Решение ГПЗ-1, когда оба пересекающихся объекта занимают проецирующее положение
Алгоритм ГПЗ-1а: Если оба объекта перпендикулярны к одной и той же плоскости проекций, то они пересекаются по прямой (прямым), перпендикулярной к этой же плоскости проекций.
Типовая задача 14 (рис. 81): Построить линии пересечения двух цилиндрических поверхностей.
Кратко запишем условие задачи.
Дано: поверхности и .
Построить: m,n= ∩ Решение (рис. 82)
1.Анализ пересекающихся объектов и их расположение.П1 ; П1 ГПЗ-1а; 1 и 1 – вырожденные проекции.
2.Находим на горизонтальной проекции точки пересечения вырожденных проекций поверхностей, которые по алгоритму являются горизонтально-проецирующими
|
прямыми m1,n1 = 1 ∩ 1 . |
m2,n2 |
строим из условия принадлежности поверхностям и . |
Рис. 81 |
Рис. 82 |
Алгоритм ГПЗ-1б: Если объекты перпендикулярны к разным плоскостям проекций, то две проекции искомой точки или линии пересечения уже есть на чертеже, т.к. они совпадают с вырожденными проекциями этих объектов (их надо только обозначить). Задача сводится к построению третьей проекции точки или линии пересечения (если необходимо).
Типовая задача 15 (рис. 83): Построить точки пересечения фронтально-проецирующей прямой с го- ризонтально-проецирующим цилиндром на трёхкартинном чертеже.
Кратко запишем условие задачи.
Дано: поверхность и прямая l. Построить: M,N=l∩ Решение (рис. 84)
1. Анализ пересекающихся объектов и их расположе-
ние.
П1; l П2 ГПЗ-1б;
1 и l2 – вырожденные проекции объектов.
2.По алгоритму: M1,N1 = 1∩l1; M2,N2 = l2 .
3.Для построения профильных проекций точек вводим
|
базовую плоскость ( 1, 3)‖П2 . Измеряя удаления точек M1 и |
|
|
N1 от 1 на горизонтальной проекциии откладывая их от 3 |
на |
|
профильной проекции, получим M3 и N3. |
|
Рис. 83 |
4.Определяем видимость прямой методом конкури- |
Рис. 84 |
рующих точек (на прямой и поверхности). |
|
|
Решение ГПЗ-2, когда один из 2-х пересекающихся объектов занимает проецирующее положение
Алгоритм ГПЗ-2: Если один из пересекающихся объектов занимает проецирующее положение, то одна проекция искомой точки или линии пересечения уже есть на чертеже, т.к. она совпадает с его вырожденной проекцией. Остальные проекции точки или линии пересечения строятся из условия принадлежности их непроецирующему объекту.
Типовая задача 16 (рис. 85): Построить линию пересечения конуса вращения горизонтальнопроецирующей плоскостью.
38
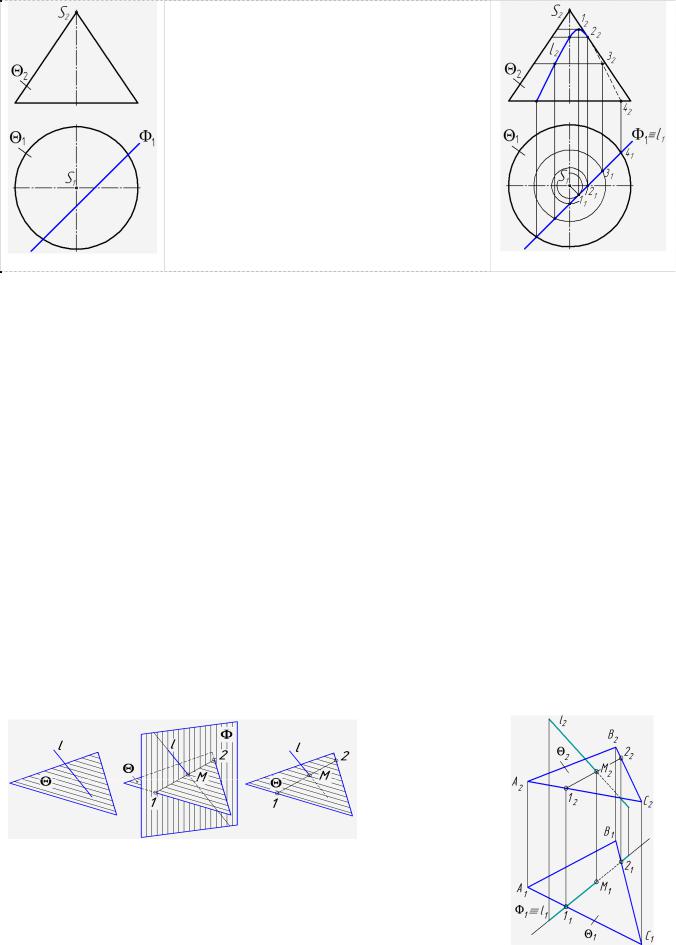
39
Кратко запишем условие задачи. Дано: поверхность и плоскость .
Построить: l= ∩
Решение (рис. 86)
1. Анализ пересекающихся объектов и их расположение.
|
П1 ; |
|
|
- непроецирующий объект |
ГПЗ-2; |
|
1 – вырожденная проекция плоскости. |
|
|
2. По алгоритму: l1 = 1; |
|
|
l2 – строим из условия принадлежности конусу. |
|
|
Плоскость параллельна оси конуса, поэтому в |
|
|
сечении получаем гиперболу. Её горизонтальная |
|
|
проекция совпадает с вырожденной проекцией |
|
|
плоскости на участке перекрытия её очерком |
|
Рис. 85 |
(окружностью) конуса. |
Рис. 86 |
2.1. Намечаем на ней опорные и промежуточные точки. Опорные точки ограничивают линию пере-
сечения справа и слева, сверху и снизу, спереди и сзади, разделяют её на видимые и невидимые части. Вершина параболы будет располагаться в ближайшей к оси конуса точке 11 . Через эту точку про-
ходит её ось симметрии. Отметим (∙)21 – границу видимости параболы на фронтальной проекции, про-
межуточную (∙)31 и нижнюю (∙)41. Симметричные им точки не обозначаем.
2.2. Через отмеченные точки на поверхности конуса проводим окружности, строим их фронтальные проекции и, на пересечении с вертикальными линиями связи, получаем точки гиперболы, которые плав-
но соединяем с учётом её видимости. ГПЗ-2 включает построение сечений всех объектов.
Решение ГПЗ-3, когда оба пересекающихся объекта не занимают проецирующее положение (общий случай решения позиционных задач)
осуществляется методом вспомогательных секущих поверхностей (плоскостей и сфер). Сущность метода заключается в том, что пространственную задачу построения точки или линии пересечения объектов сводят к поверхностной задаче построения отдельной точки или ряда точек линии пересечения. Метод сфер применяется для построения линий пересечения тел вращения, оси которых пересекаются и лежат в плоскостях уровня. В остальных случаях используют метод вспомогательных секущих плоскостей.
Метод вспомогательных секущих плоскостей
Объекты пересекаются в зоне линии пересечения проецирующими плоскостями или плоскостями уровня так, чтобы в сечении с каждым объектом получались бы простые для построения фигуры (прямые, многоугольники, окружности).
Типовая задача 17 (рис. 87, 88): Построить точку пересечения прямой с плоскостью (общего положения).
Рис. 87
Запишем условие задачи. Дано: l и ( АВС). Построить: M = l ∩ . Решение (наглядное - рис. 87, на комплексном чертеже - рис. 88).
1. Анализируем пересекающиеся объекты и их расположение.
l и - непроецирующие объекты ГПЗ-3; Метод секущих плоскостей.
Рис. 88
39
|
40 |
|
|
|
|
|
|
|
|
2. Заключаем прямую в горизонтально-проецирующую плоскость и строим линию 12 пересечения |
|||||||||
её с заданной плоскостью: |
11 21 ≡ 1 ∩ 1; |
|
|
|
|
|
|
|
|
|
12 22 из условия 2. |
|
|
|
|
|
|
|
|
3. Строим точку М - пересечения объектов |
|
|
|
|
|
|
|
|
|
М2 = 12 22 ∩ l2; |
|
|
|
|
|
|
|
|
|
М1 из условия l1. |
|
|
|
|
|
|
|
|
|
4. Определяем видимость прямой l методом конкурирующих точек. |
|
|
|
|
|
|
|||
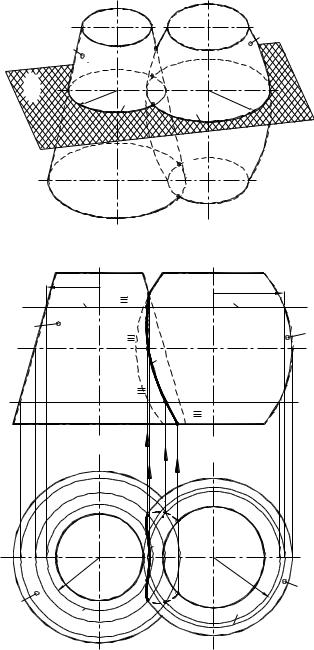
Типовая задача 18 (рис. 89-90): Построить линию пересечения конуса с тором. |
|
|
|||||||
|
Дано: поверхности и . |
|
|
|
|
|
|
||
|
Построить: l= ∩ |
|
|
|
|
|
|
||
Решение (наглядное - рис. 89, на комплексном чертеже - рис. 90). |
|
|
|
|
|
|
|||
1. Анализ пересекающихся объектов и их расположение. |
|
|
|
|
|
|
|
||
и - усечённые поверхности вращения: конус и |
|
|
|
|
|
|
|
|
|
закрытый самопересекающийся тор – являются не- |
|
|
|
|
|
|
|
|
|
проецирующими объектами и пересечение их пред- |
|
|
|
|
A |
|
|
||
ставляет ГПЗ-3. Оси вращения поверхностей пер- |
|
|
|
|
|
|
|||
пендикулярны 1 , что позволяет использовать метод |
|
' |
|
|
1' |
|
|
|
|
вспомогательных секущих плоскостей. |
|
n |
|
|
|
R |
|||
2. Определяем опорные точки линии пересече- |
|
r |
1 |
m |
|||||
ния. Верхняя точка – А2 находится на пересечении |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||
главных меридианов, расположенных в одной фрон- |
|
|
|
|
|
|
|
|
|
тальной плоскости уровня, которая также является |
|
|
|
|
|
B' |
|
|
|
для объектов общей плоскостью симметрии. Основа- |
|
|
|
|
|
|
|
||
ния поверхностей – параллели – пересекаются в |
|
|
|
|
|
|
|
|
|
нижних точках В1 и В1’. Точки 21, 21', принадлежащие |
|
|
|
|
|
B |
|
|
|
экватору тора, ограничивают видимость горизон- |
|
|
|
|
|
|
|
||
тальной проекции линии пересечения. Другие проек- |
|
|
|
Рис.89. |
|
|
|||
ции опорных точек находим с помощью линий связи. |
|
|
|
|
|
||||
3. Находим промежуточные точки линии пересечения. |
|
|
|
|
|
|
|
||
Рассекаем поверхности и секущей плоскостью |
|
r |
|
|
A2 |
|
R |
||
2’‖ 1 , строим радиусами r и R параллели n и m |
|
|
|
|
|||||
|
n |
12 |
1'2 |
|
|||||
2' |
|
|
|
m |
|||||
и находим точки их пересечения |
2 |
|
|
|
|
|
|
||
1, 1' = n ∩ m . Аналогично рассекаем поверхности |
|
2 |
2' |
|
|
|
2 |
||
и плоскостями 2’’, 2’’’и находим точки 2,2',3,3’. |
2'' |
|
|
|
|
|
|||
|
2 |
2 |
|
|
|
|
|||
|
|
|
l2 |
|
|
|
|||
4. Соединяя построенные точки с учётом ви- |
|
|
|
|
|
|
|
||
димости, − получим линию пересечения l. За ви- |
|
|
|
3 |
3' |
|
|
|
|
димую часть линии пересечения принимают ту |
|
|
|
|
|
|
|||
'''2 |
|
|
2 |
2 |
|
|
|
||
её часть, которая принадлежит обеим видимым |
|
|
|
|
B2 |
B2 |
|
||
поверхностям. На горизонтальной проекции ви- |
|
|
|
|
|
|
|
|
|
димой является вся коническая и верхняя часть (до |
|
|
|
|
|
|
|
|
|
экватора) поверхности тора. Точки линии пересе- |
|
|
|
|
|
|
|
|
|
чения, расположенные выше экватора – видимые. |
|
|
|
|
|
|
|
|
|
Метод вспомогательных секущих сфер |
|
|
|
2'1 |
|
3' |
|
|
|
|
|
|
|
1 |
|
|
|||
применяется для построения линий пересече- |
|
|
|
1 |
|
B'1 |
|
|
|
|
|
|
1' |
|
|
|
|||
ния поверхностей вращения, оси которых пе- |
|
|
|
A1 |
l1 |
|
|
|
|
ресекаются и лежат в плоскостях уровня. |
|
r |
|
|
|
|
|
R |
|
Метод очень эффективен т.к. позволяет за |
|
|
11 |
|
|
|
|||
|
|
|
B |
|
|
||||
|
|
|
|
|
|
||||
одно построение сферы Rmin |
определить поло- |
|
|
|
|
|
1 |
|
|
1 |
|
|
21 |
31 |
|
1 |
|||
n |
|
|
m |
||||||
жение линии пересечения, но требует точно- |
|
|
|||||||
|
|
|
|
|
|
|
|||
сти в исполнении. Этот метод основан на |
|
|
|
|
|
|
|
|
|
свойстве сферы, пересекаться с любой по- |
|
|
|
|
|
|
|
|
|
верхностью вращения, ось которой проходит через |
|
|
Рис. 90 |
|
|
||||
центр сферы, по окружностям, перпендикулярным |
|
|
|
|
|
|
|
||
40