
- •Производная функции.
- •Производные высших порядков.
- •2.Экстремумы.
- •3.Вогнутость.
- •4.Перегибы.
- •5.Ассимптоты.
- •Исследование функции
- •Неопределённый интеграл.
- •Геометрические приложения определенного интеграла
- •Повторный интеграл
- •Основные теоремы о степенных рядах.
- •Ряд Тейлора.
- •Разложение основных функций в ряд Тейлора.
- •Некоторые применения.
- •Числовые ряды комплексных чисел.
- •Степенные ряды комплексных чисел.
- •Периодичность.
- •П zоказательная функция.
- •Дост. Условия дифференцируемости.
- •Комплексно-значная формула комплексной переменной.
- •Правило обхода сложного контура.
- •Интеграл с переменным верхним пределом.
- •Интегральная формула Коши.
- •Решение неоднородного уравнения.
- •Метод вариации произвольных постоянных.
- •Решение неоднородного линейного уравнения с постоянными коэффициентами, где правая часть имеет специальный вид.
- •Метод вариации произвольных постоянных.
- •Основная теорема о вычетах
- •Вычисление вычетов в приложении к несобственным интегралам
- •Лемма Жордана
- •Решение дифференциальных уравнений.
- •Свертка функций.
Основные теоремы о степенных рядах.
(1)
![]() (-R,R)
(-R,R)
Теорема 1.
Ряд (1) мажорируем на любом промежутке
[-p;p]
![]() (-R,R).
(-R,R).
Доказательство.


-pp
-R0R
(*)
![]() мажоранта
ряда (1)
мажоранта
ряда (1)
|x|![]() p-> |
p-> |![]() |
|![]() |
|![]() |
|![]()
Теорема 2.(о почленном интегрировании степенного ряда)
Ряд (1) можно интегрировать почленно на любом отрезке, лежащем в интервале сходимости.
Доказательство.
В доказательстве исходить из того, что
можно интегрировать почленно на любом
промежутке [-p;p]
![]() (-R,R).
(-R,R).
Теорема 3.(о непрерывности суммы степенного ряда)
S(x) непрерывна на (-R,R).
Теорема 4. (о почленном дифференцировании)
(2)
![]()
Доказать:
Интервал сходимости (2) совпадает с
интервалом сходимости (1) . Это (-R,R),
причемf(x)
=
![]() .
.
Если (2) мажорируем повсюду, то там можно его почленно дифференцировать.
Доказательство.
(-R,R) – интервал сходимости ряда (1)

![]()


-R-p0pR
Покажем, что (2) мажорируем на любом промежутке [-p;p].
Возьмем p<![]() <R.
<R.
|x|![]() p
p
|![]() |
|![]() n*|
n*|![]() |
|![]()
![]() n|
n|![]() |
|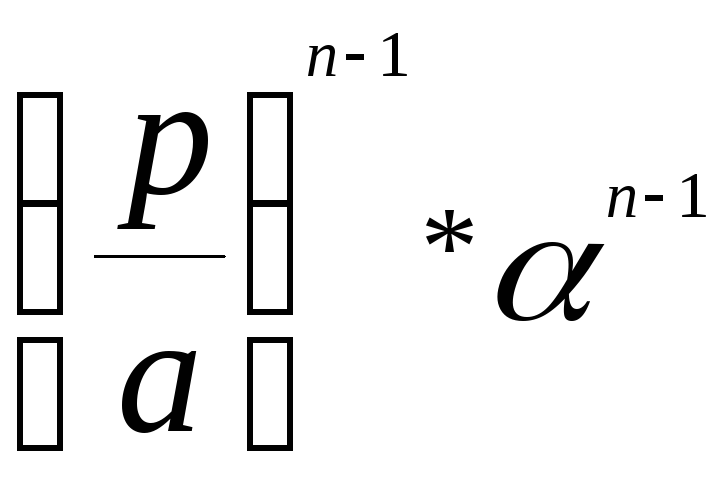 =
=
![]()
![]()
![]()
![]() - > сходится ->
- > сходится ->![]() |
|![]() M
M
(**)
![]()
![]()
![]() сходится??
сходится??
Исследуем (**) по Даламберу:
![]()
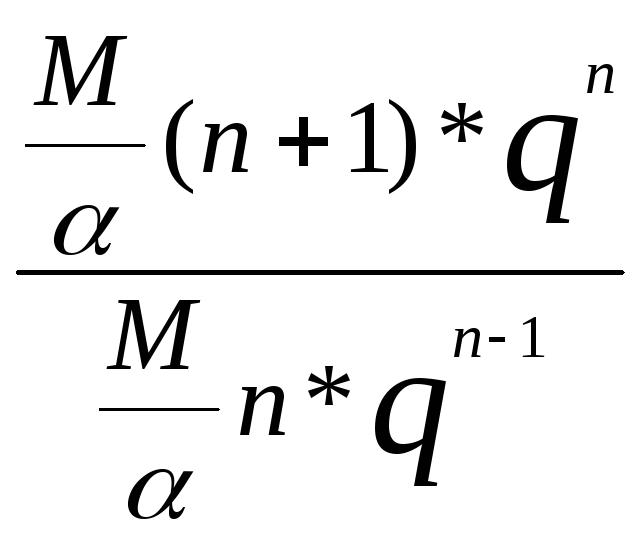 =q<1 -> (**) – сходится
-> является мажорантой ряда (2).
=q<1 -> (**) – сходится
-> является мажорантой ряда (2).
Ряд (2) будет сходится абсолютно в любой точке интервала сходимости ряда (1) -> его интервал сходимости не меньше, чем у ряда (1).
Покажем, что ряд (2) расходится вне интервала (-R,R). Доказательство исходит из противного.





-RRx1x0R<x1<x0
Предположим, что ряд (2) сходится в x0 -> ряд (2) можно интегрировать почленно на [0,x1].
![]() =
=
![]() =
=![]() - > сходится, а ряд (1) расходится вx1
-> имеем противоречие.
- > сходится, а ряд (1) расходится вx1
-> имеем противоречие.
Ч.т.д.
Замечание. Степенной ряд можно сколько угодно раз почленно дифференцировать и интегрировать. Интервал сходимости от этого не изменится.
Ряд Тейлора.
Формула Тейлора:
Если y=f(x) имеет вU(a) непрерывные производные до порядка (n+1), тогда ее можно представить формулой:
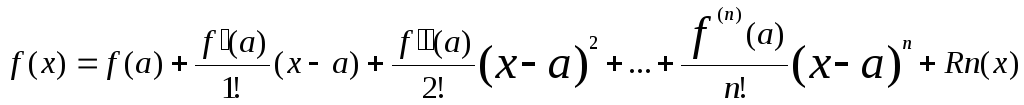
Где Rn(x) =
 (a+θ(x-a)), 0< θ <1.
(a+θ(x-a)), 0< θ <1.
Теорема.Пустьf(x)
имеет в окрестности точки а производные
любого порядка,![]() =
0, тогда ее можно представить рядом
Тейлора.
=
0, тогда ее можно представить рядом
Тейлора.
Замечание. В окрестности точки а ряд должен сходиться.
![]()
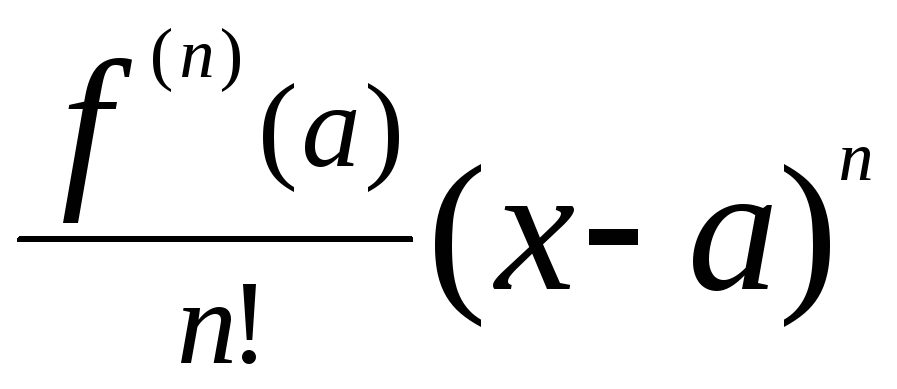 не сойдется кf(x),
т.к. мешает ост.член.
не сойдется кf(x),
т.к. мешает ост.член.
Если а=0, то ряд Тейлора переходит в ряд Маклорена:
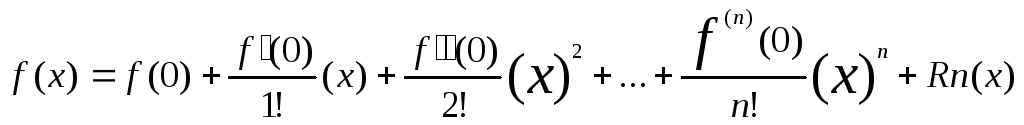
Разложение основных функций в ряд Тейлора.
1) f(x)=
![]() f(0)=1
f(0)=1
![]()
![]()
![]() =
=
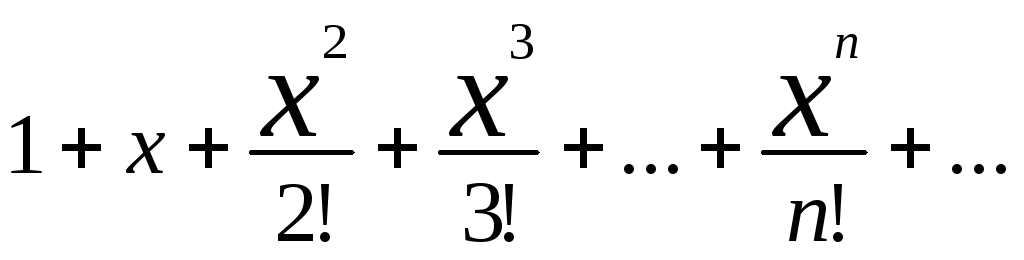 сходится всюду ->
сходится всюду ->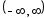
2) f(x)=sinxf(0)=0
![]() cosx
cosx![]()
![]()
![]()
![]()
![]()
sinx=
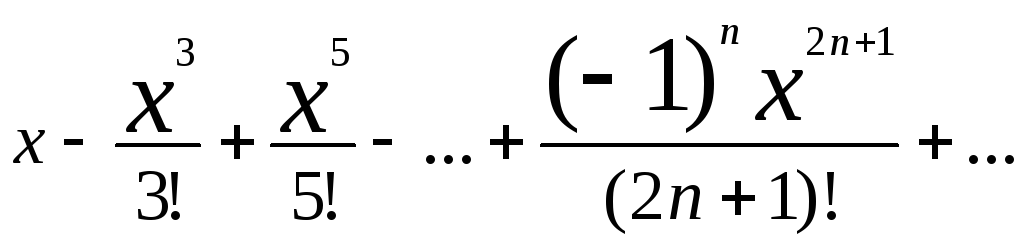 сходится всюду ->
сходится всюду ->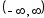
lim |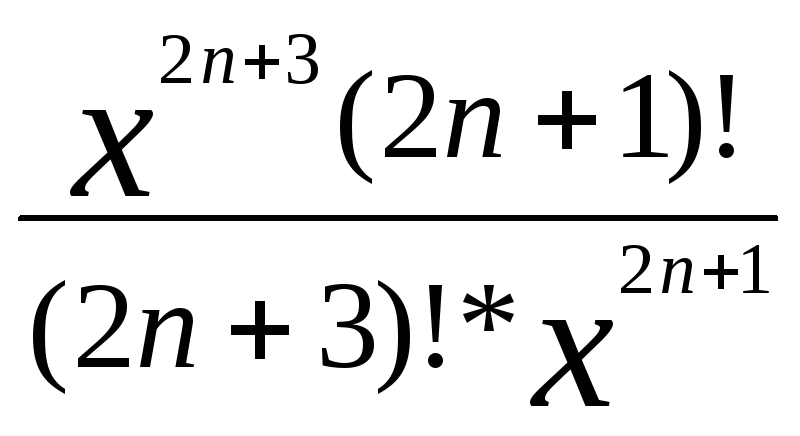 |
=
|
=![]() lim
lim![]() =0
=0
3) f(x)= cos x
cosx=
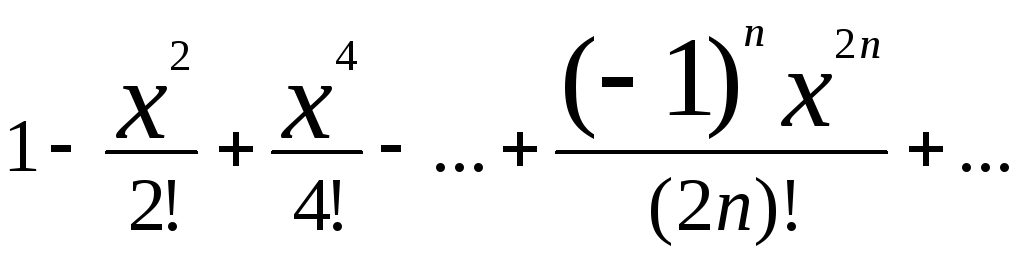 сходится всюду ->
сходится всюду ->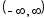
Примечание.
![]() =
=
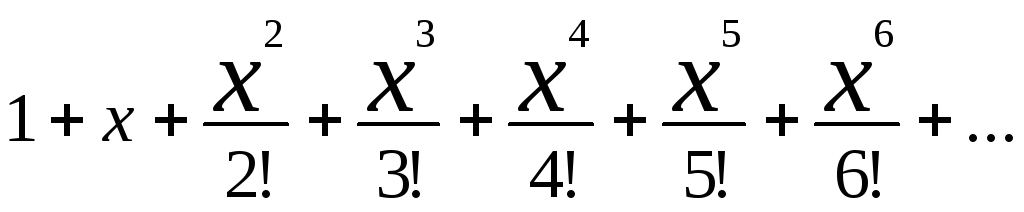
![]() =
=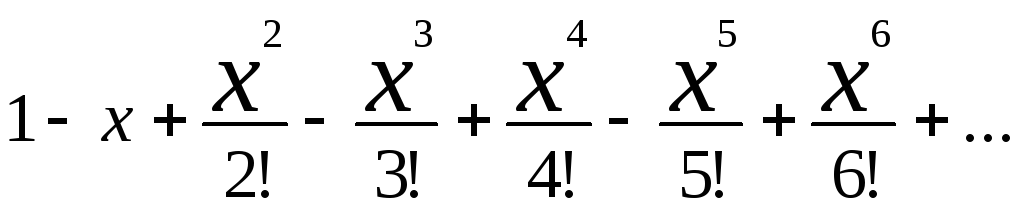
sh x = 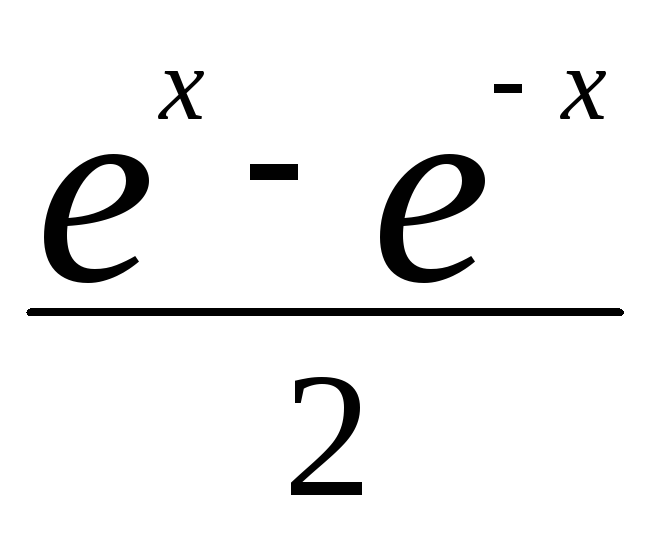 ch x =
ch x = 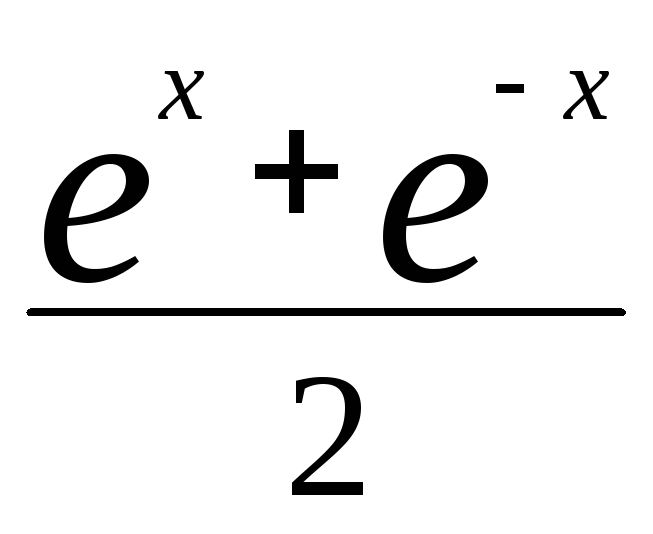
4) f(x) = ch x
chx=
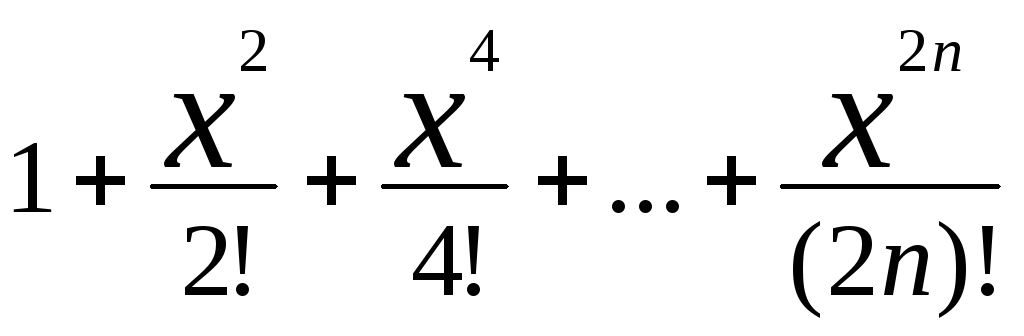 сходится всюду ->
сходится всюду ->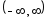
5)f(x)=shx
shx=
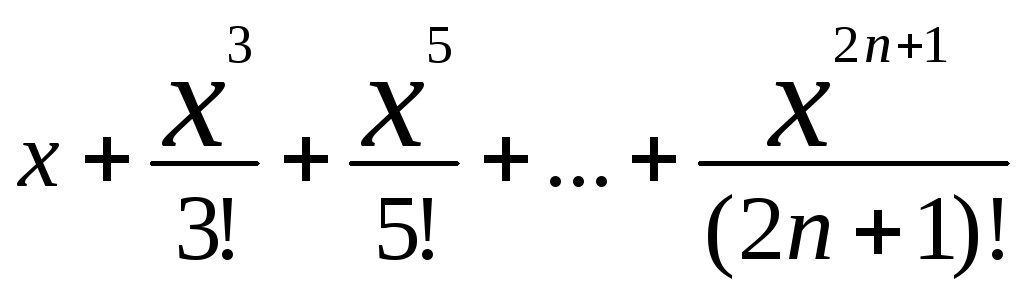 сходится всюду ->
сходится всюду ->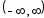
6) f(x) =
![]() f(0)=1
f(0)=1
![]() m
m![]()
![]()
![]()
![]()
![]() =1+mx+
=1+mx+![]()
сходится на (-1,1)
Примечание.
R=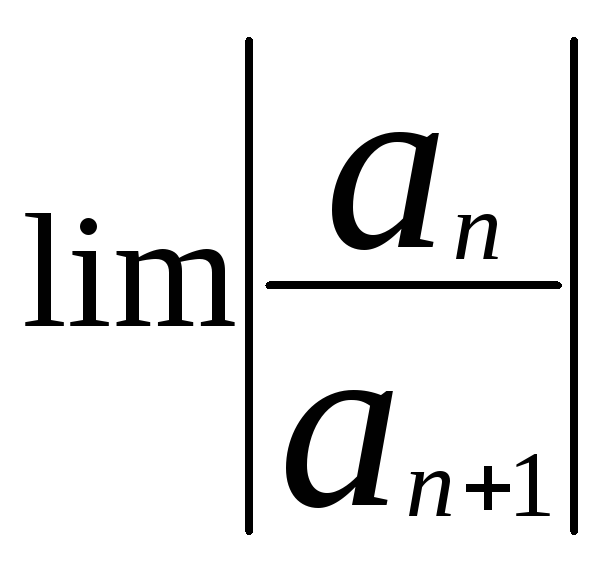 =lim
=lim
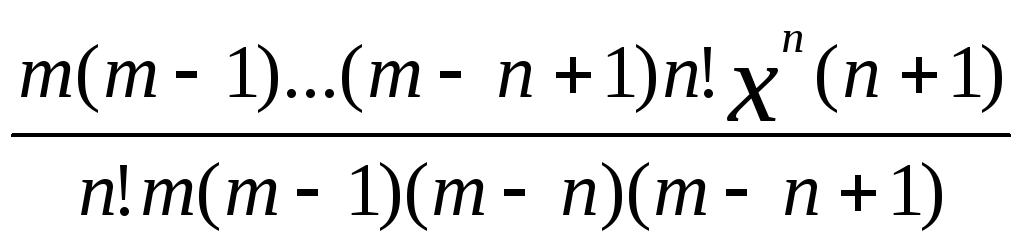 =lim|
=lim|
![]() |
= 1
|
= 1
При m=-1 :
![]() q = - x;
q = - x;
![]() q = x;
q = x;
![]()
![]() 1+mx
1+mx
![]()

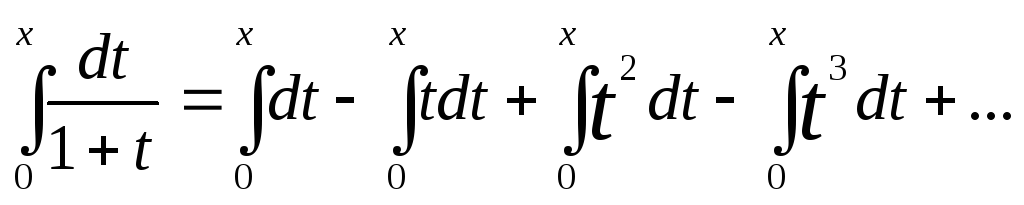
Ln|1+t|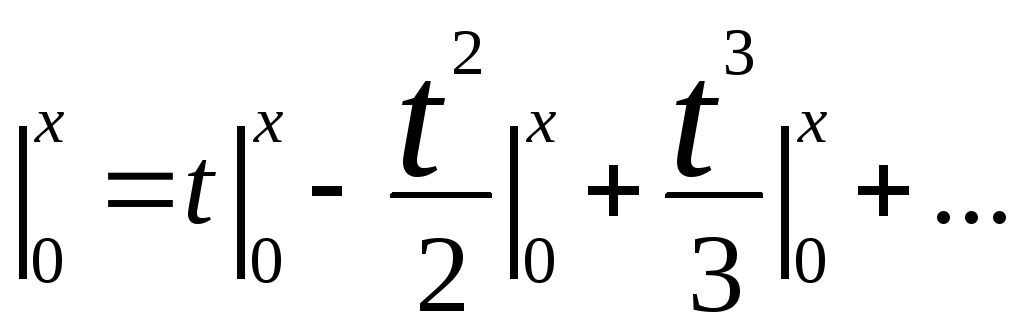
ln(1+x) =
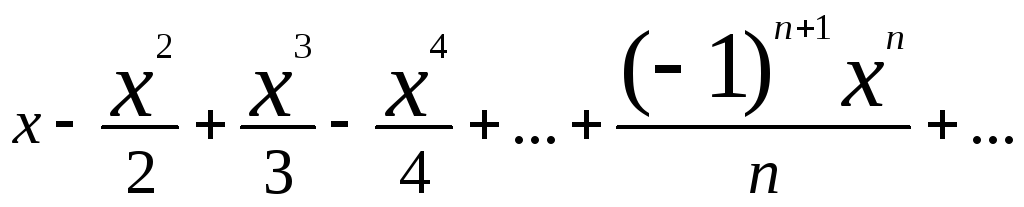
(-1,1) – интервал сходимости.
(-1,1] – область сходимости
x = -1,
![]() расходится
расходится
x= 1,
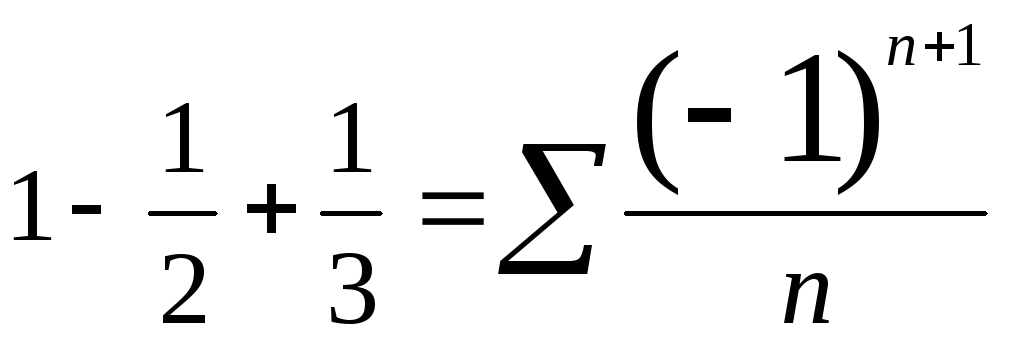 сходится
сходится
Примечание.
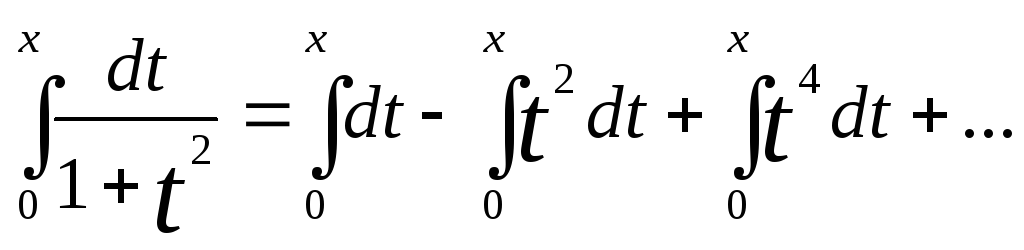
arctg t
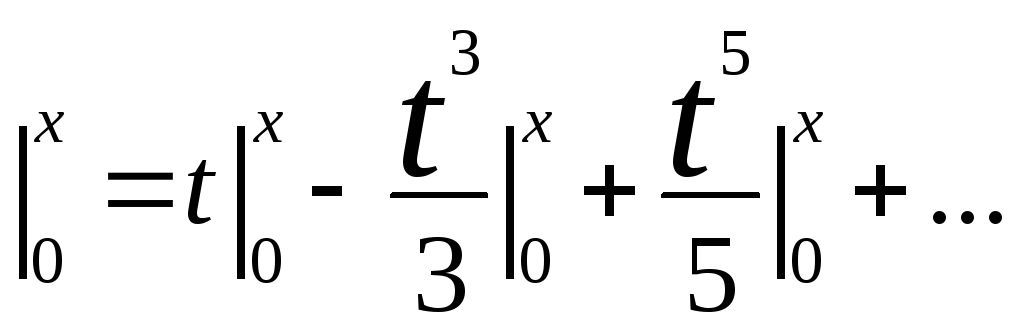
8) arctg x =
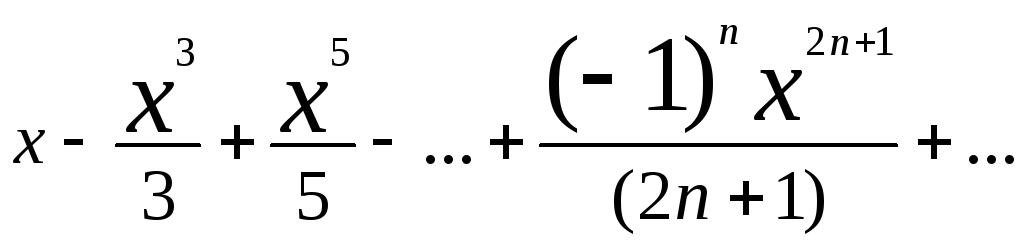 [-1;1] (-1,1)
[-1;1] (-1,1)
x=-1
![]() cx.
cx.
x=1
![]() cx.
cx.
