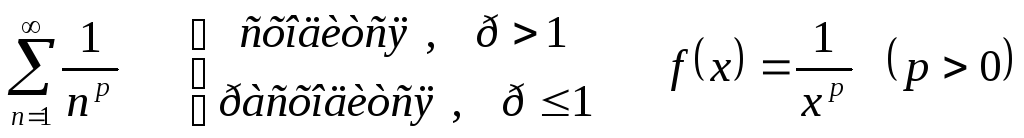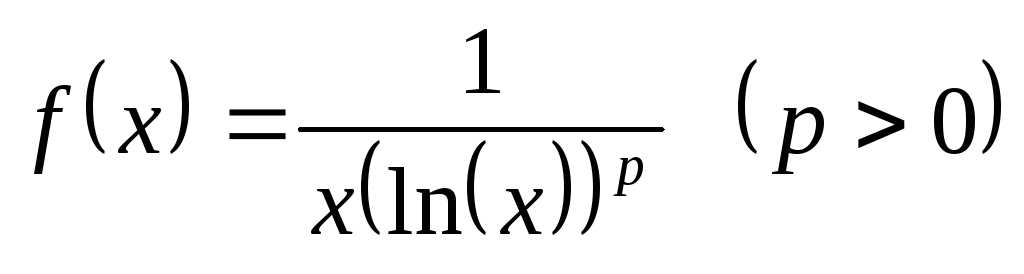Повторный интеграл

Обл. Dназывается правильной в направлении осиy, если любая прямая || оси у, проходящая через внутреннею точку областиDпересекает границу области ровно в 2х точках.

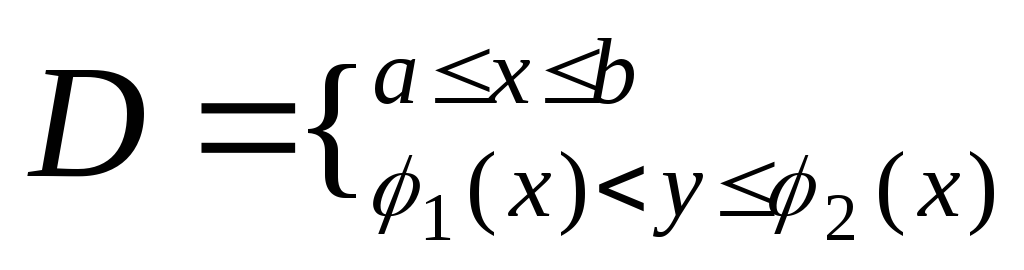
Пустьнепр. вD

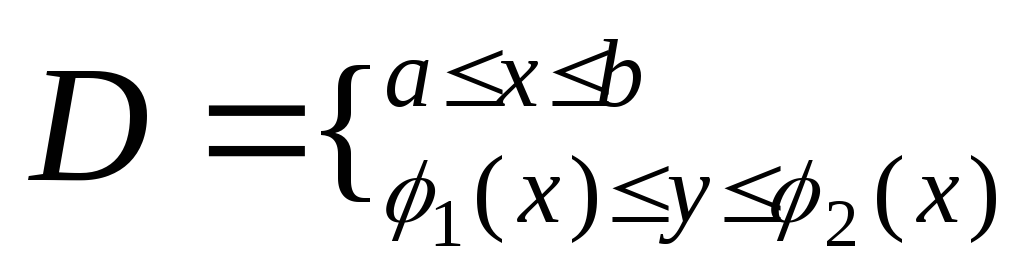
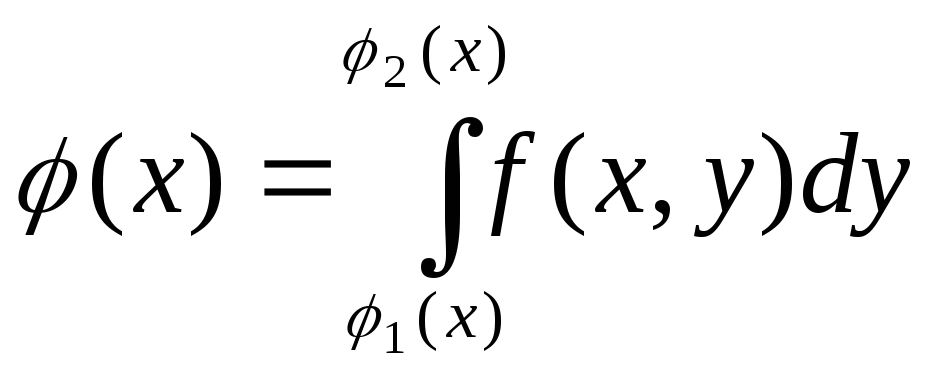
- непр. вD,и- непр.- тоже непр.

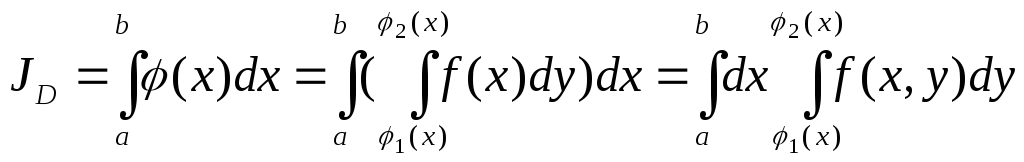
Свойства двукратного интеграла:

1. Если провести область вертикальными или горизонтальными прямыми разбить на части, то полученные части тоже будут правильными областями, причем S=S+S

2. (т.о среднем)

- непр. вD

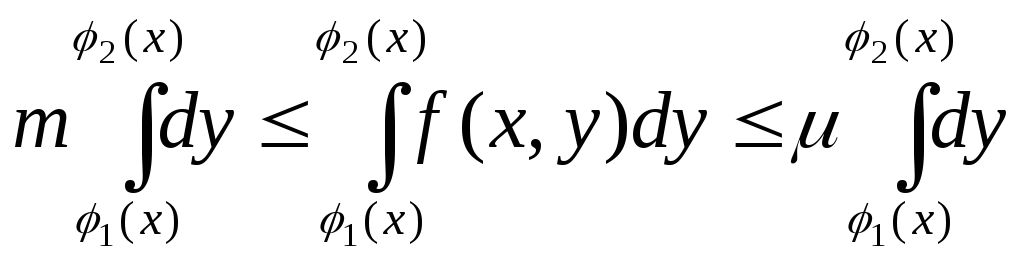
- промежуточное значение

Теорема (о равенстве двойного и двукратного интеграла)

непр. вDправ. в напр.Oy.

Доказательство:

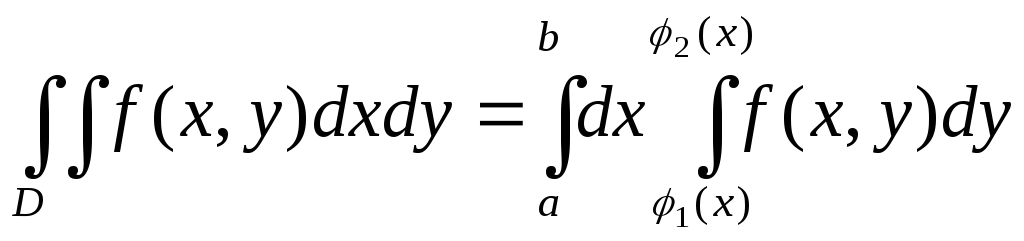
Следствия:

Если обл. D-прав, то справедливо равенство

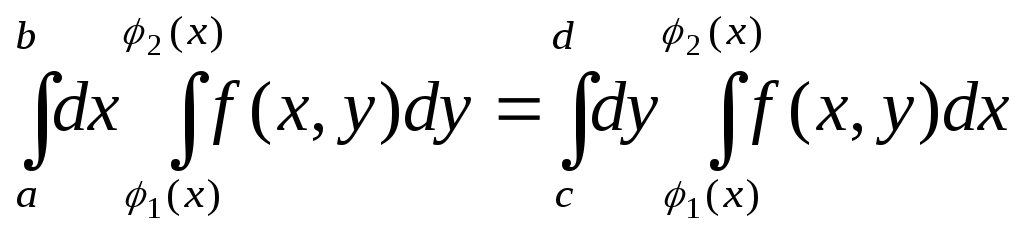- формула переменного пор-ка интегрирования.

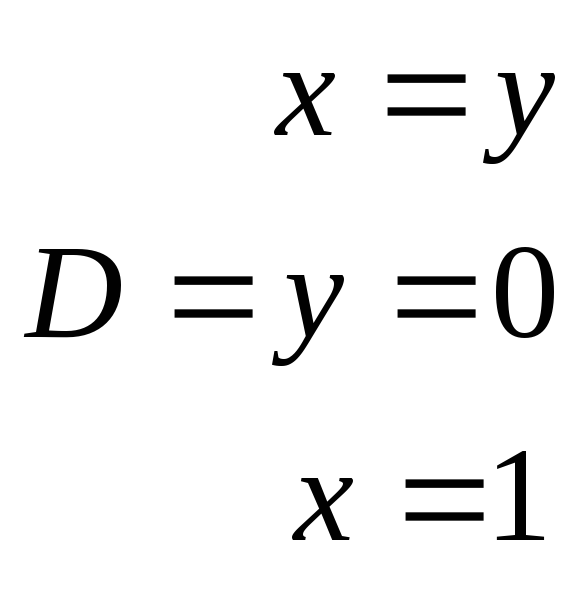
Замена переменных в двойном интеграле

(1)

Пусть формула (1) непр. диф-ны иосуществл. отошения обл. Dна обл

непр. вD(2)

Формула перехода к полярным координатам

Пример:

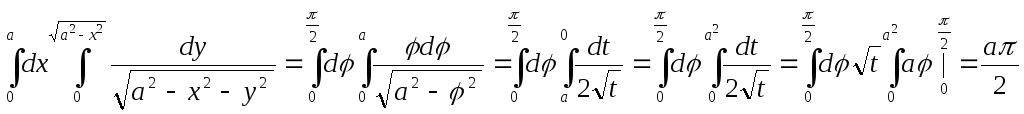
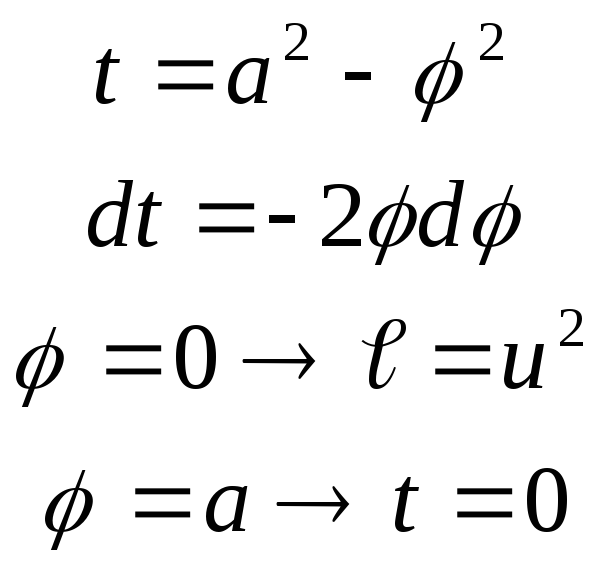
Приложение двойного интеграла.

1. Площадь области.

2. Объём тела

3. Площадь поверхности

Пример:

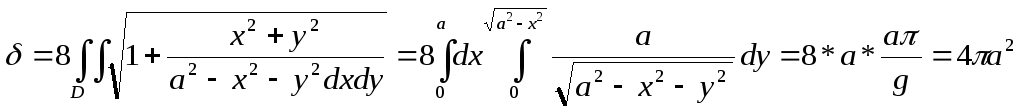
Интегралы по-мере

- Универсальное множество

- подмножество

(mesA)

1.

2.

3. ,

наоборот не верно если , то не значит что множество.

масса тела-мера.

-интегр. суммана.

так, чтоmax.diam

Свойства:

1. Линейность.

2. Аддетивность.

3. 

4. 

5. 

6. 

Тройные интегралы

- правильная двумерная обл.

1. D-прав (2-мер.)

2. Если прямая проходящая через внутреннию точку, то пересекает граници области в 2х точках.

Приложения:

1. Vтела

2. Масса тела

-плотность

- плотность

3. Центр массы.

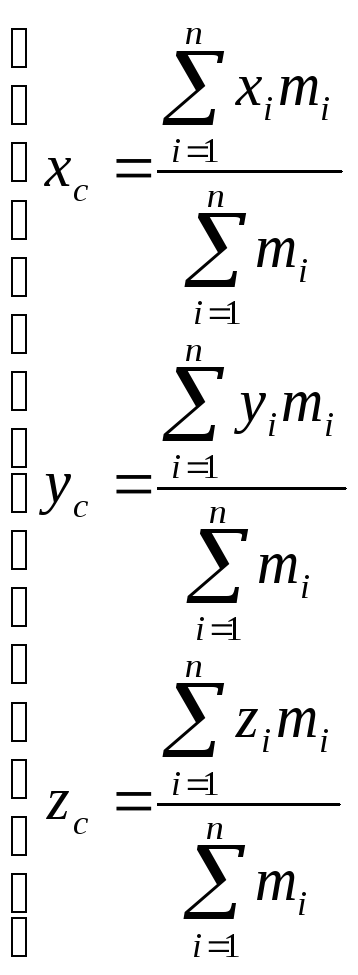
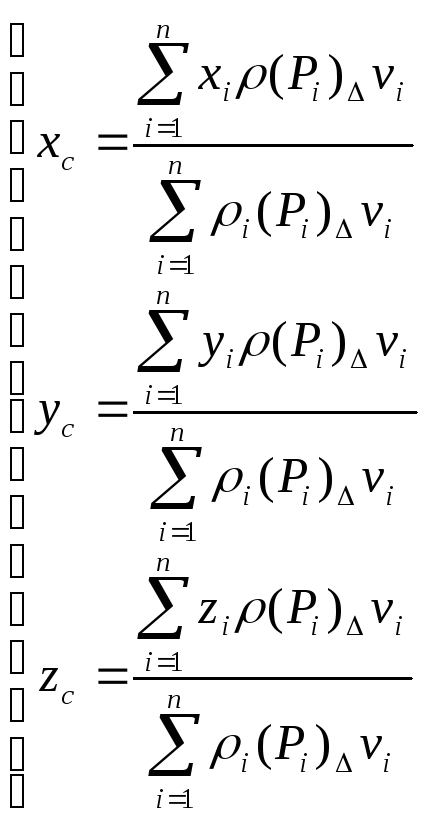
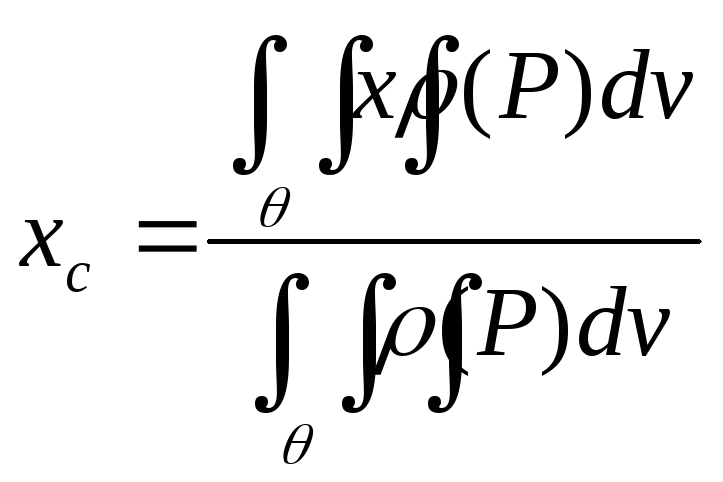
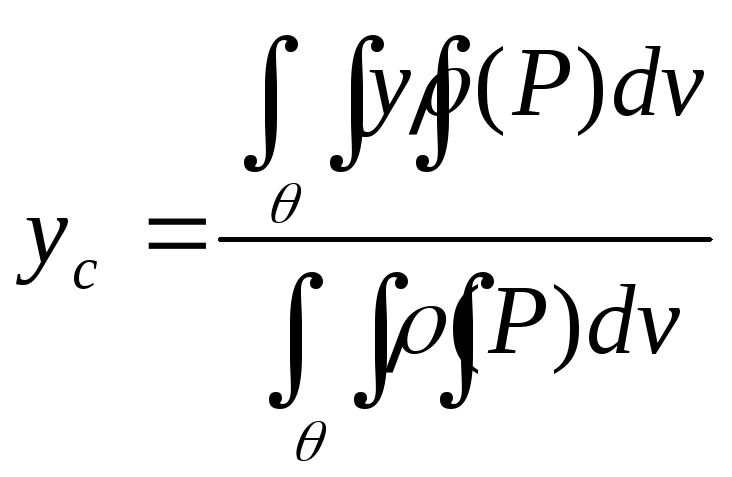
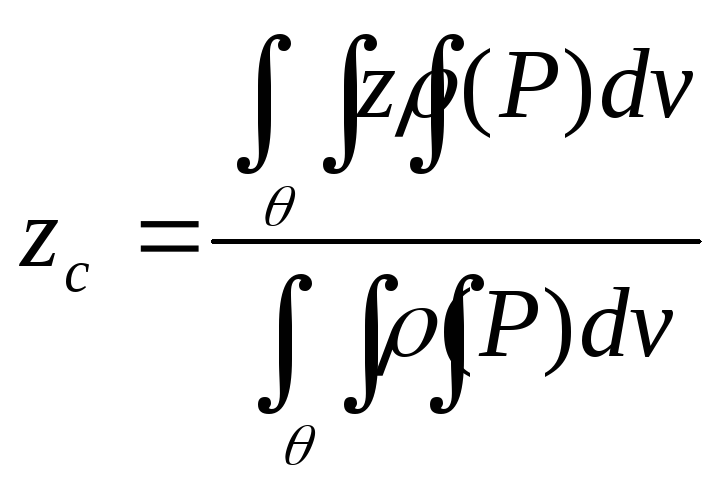
Пример:

Найти центр масс однородного тела, ограниченного поверхностью

Если

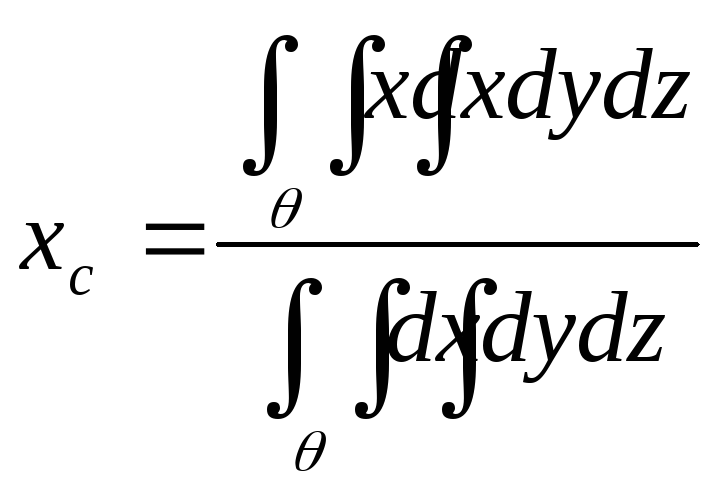
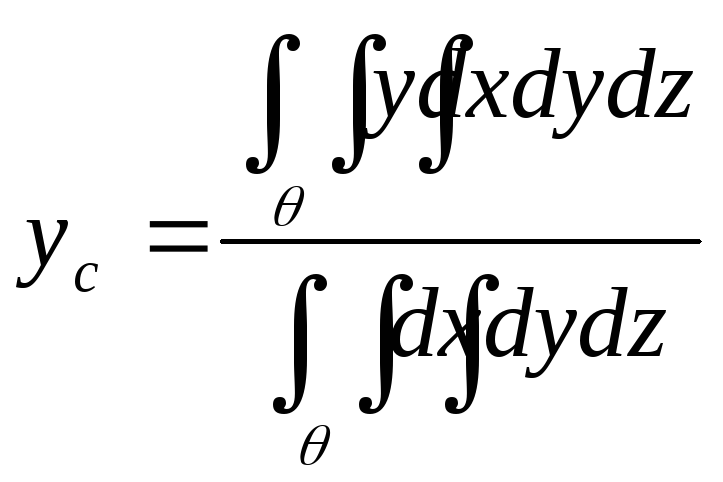, еслиx=0,y=0,тоz=h

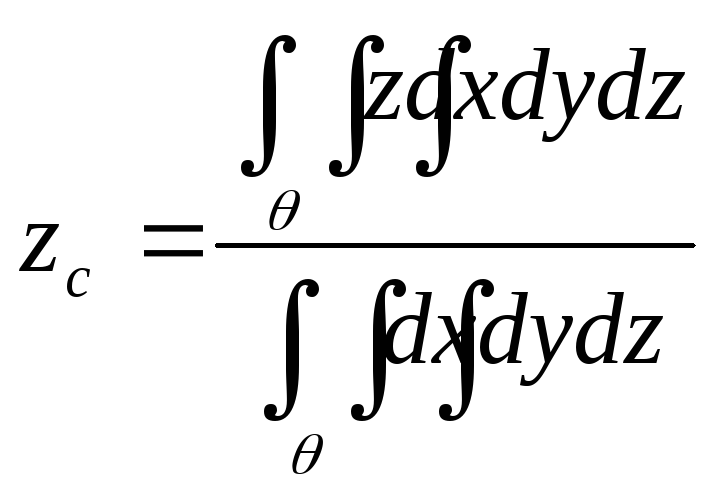
1.

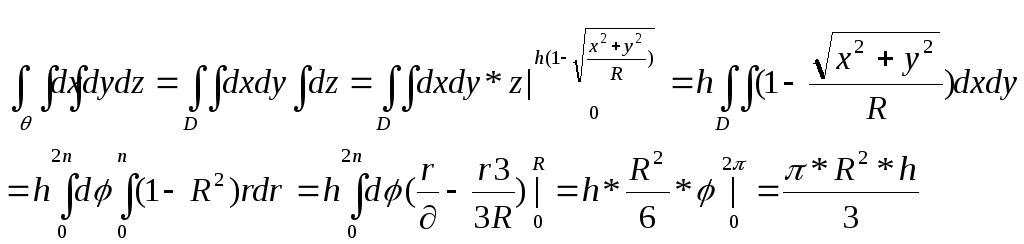
2.

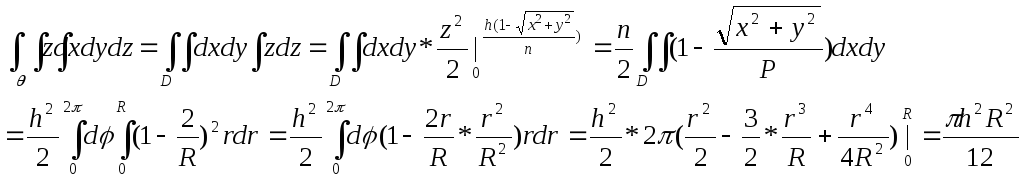
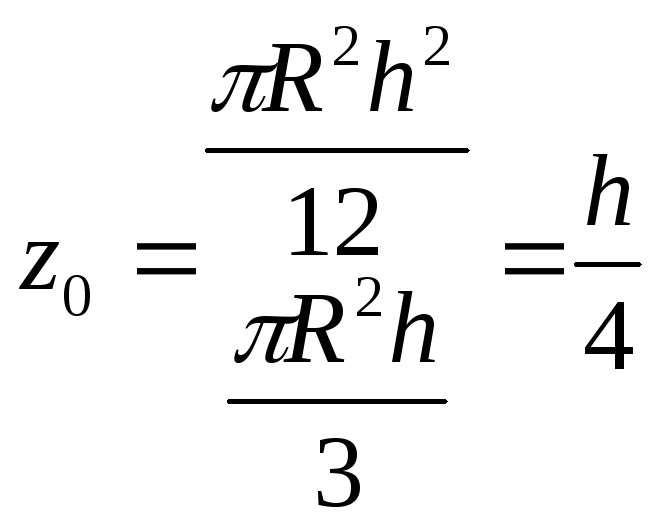
Криволинейный интеграл 1го рода

интегрируем на

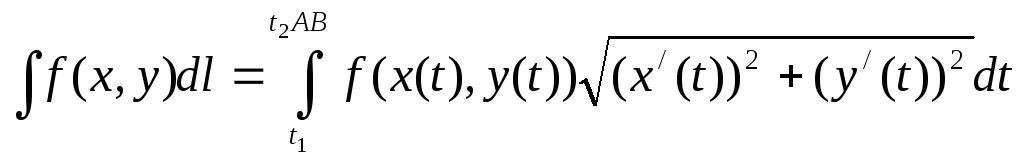
Пример:

Найти масс однородной прово. имеющей форму полуокружности.

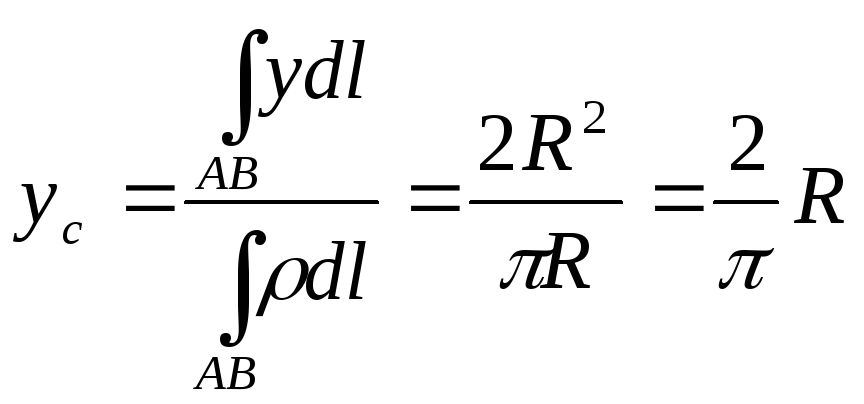
длина

Криволинейный интеграл 2го рода

непр.наAB

- на плоскости

-крив. инт. по кривой

- положит. Направление

- отр. Направление

Если мы задаём кривую

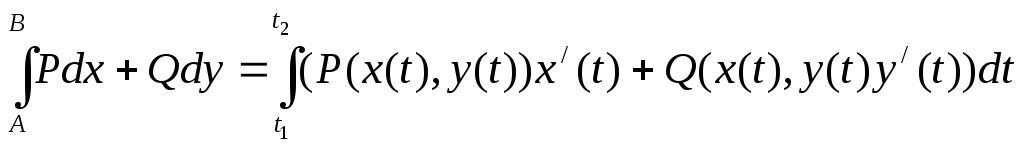
Физический смысл:

Работа на прямолинейном участке пути.

Формула Гриля

-непр. В областипоHи за его пределами

Рассмотрим:

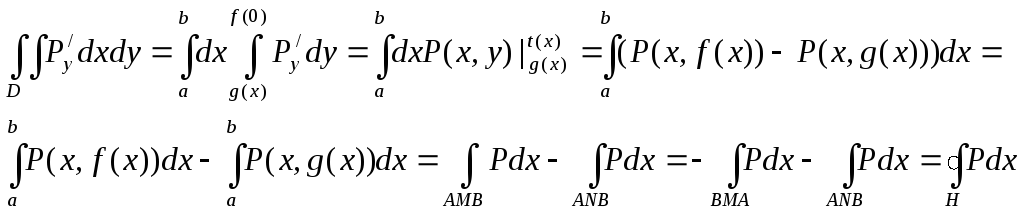
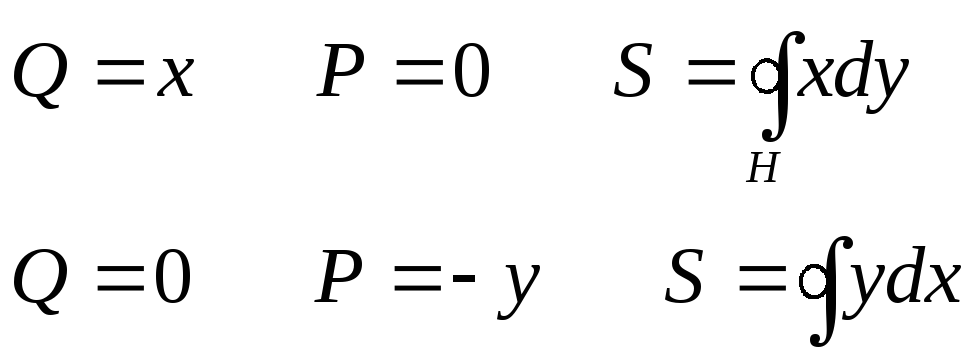
- площадь области

Пример:

Исследование ряда Дирихле

1. 

Пример:

2. 

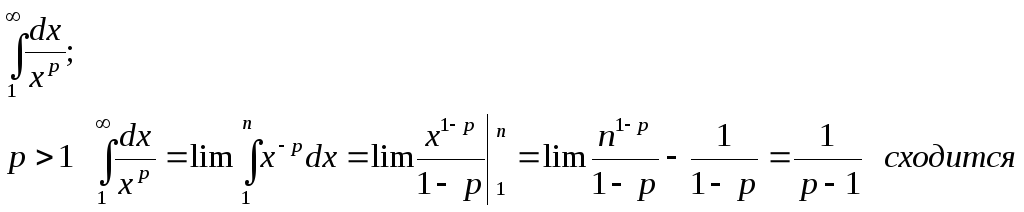
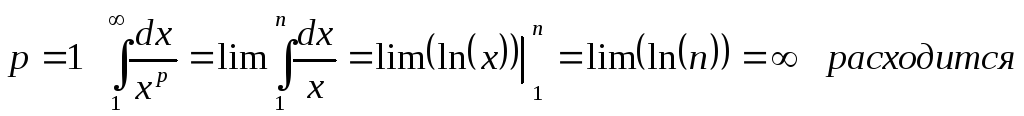
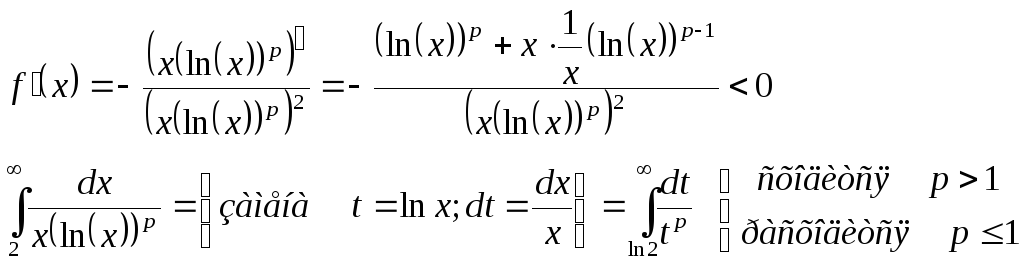
Знакопеременные ряды

Теорема(об абсолютной сходимости): Если ряд (2) сходится, то и ряд (1) тоже сходится.

Доказательство:

Рассмотрим частичную сумму:

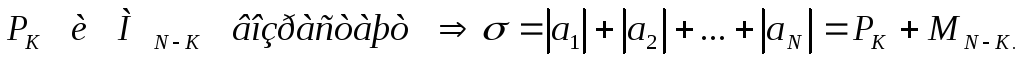
Ряд (2) сходится, то есть существует

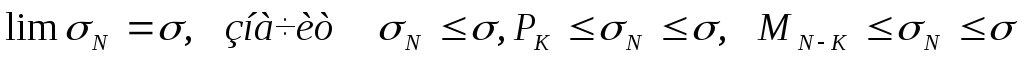
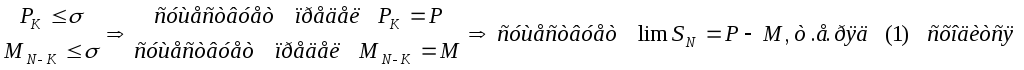Примечание – обратное неверно. Например:

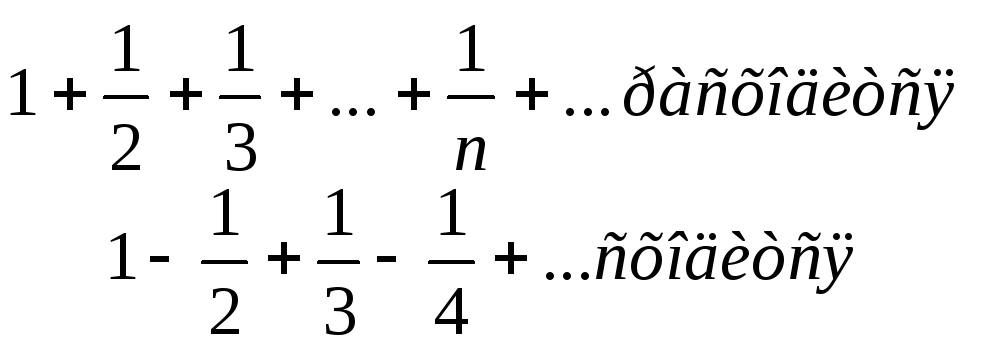
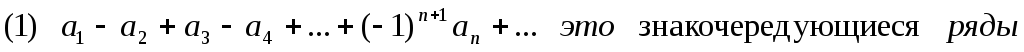
Теорема(Лейбница):

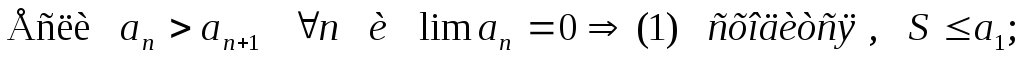
Доказательство:

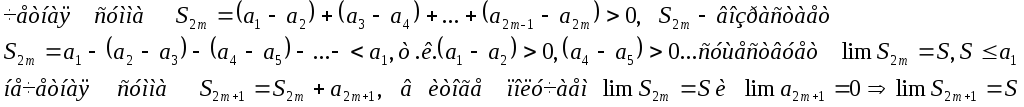
Теорема доказана.

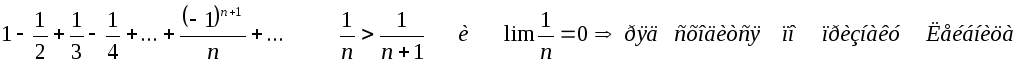
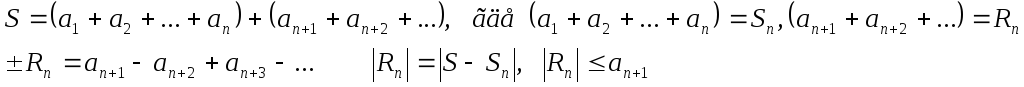
Вывод: погрешность при вычислении суммы знакочередующегося ряда не превосходит первого отброшенного члена.

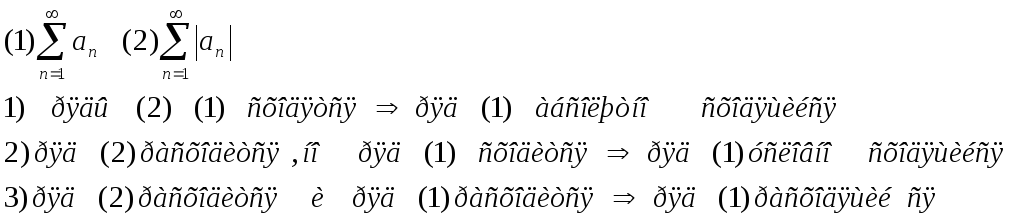
Свойство №1:

Если ряд сходится абсолютно, то он остается абсолютно сходящимся при любой перестановке его членов и сумма при этом не меняется.

Свойство№2:

Если ряд сходится условно, то при перестановке членов его может стать равной любому числу, а также можно сделать его расходящимся.

Примеры:

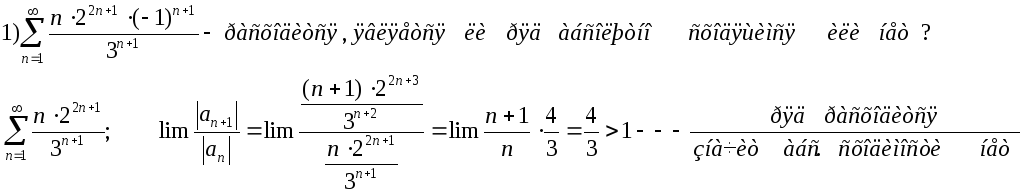
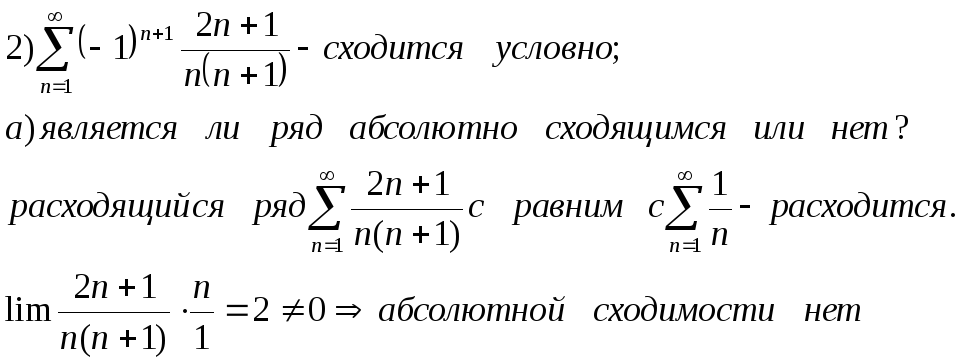
Функциональные ряды

Определение: Множество значений х, при которых ряд (1) – сходится, называется областью сходимости ряда.

Примеры:

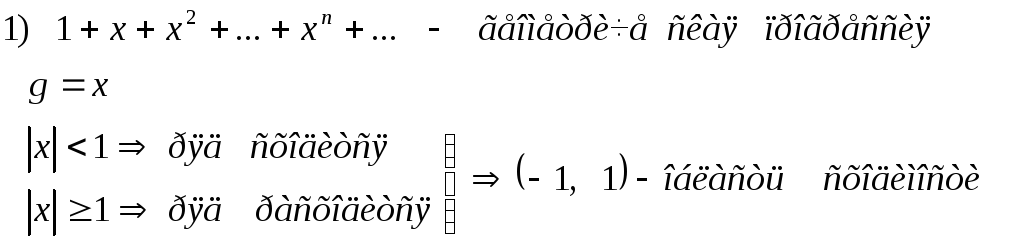
Ряд (1) называется мажорируемым на , если существует числовой положительный сходящийся ряд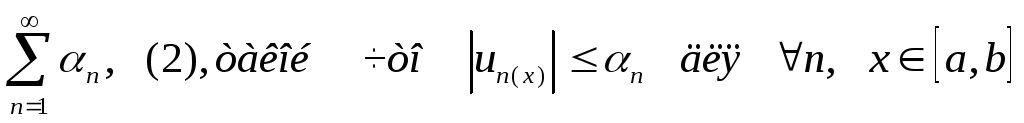, при этом (2) называют мажорантой (1).

Мажорируемый ряд сходится абсолютно.

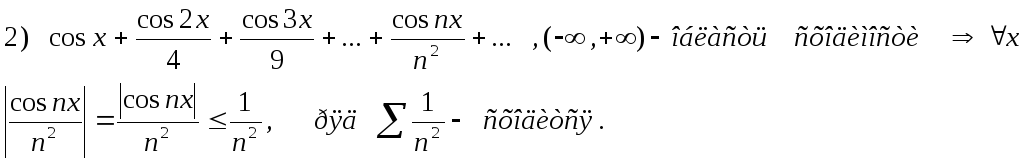
Теорема(о почленном интегрировании функционального ряда):

Пусть ряд (1) мажорируем на , тогда его можно почленно интегрировать на любомвложенном в.

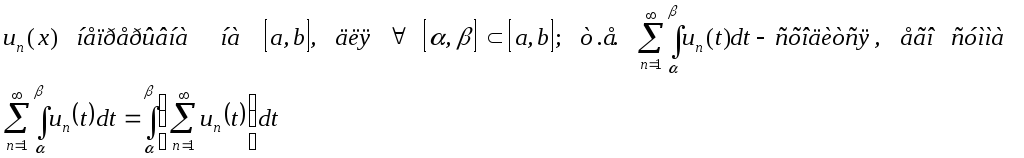
Теорема№1(о непрерывности функционального ряда)

Теорема№2(о почленном интегрировании функционального ряда):

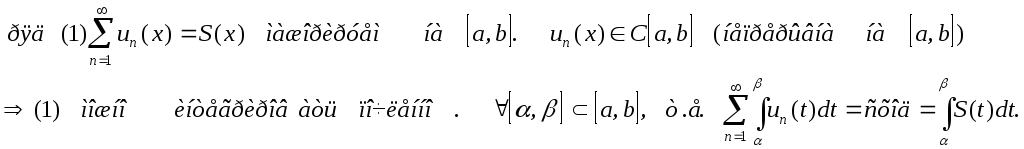
Доказательство:

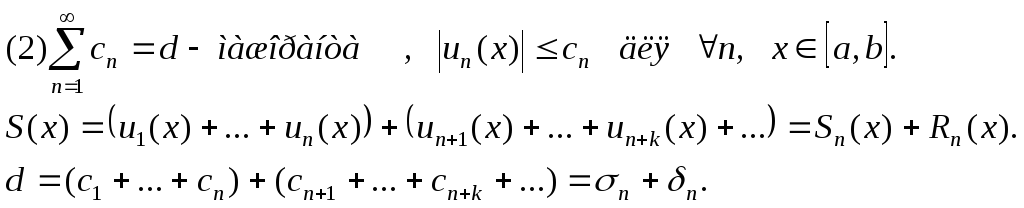
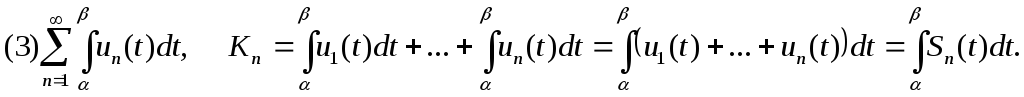
Требуется доказать

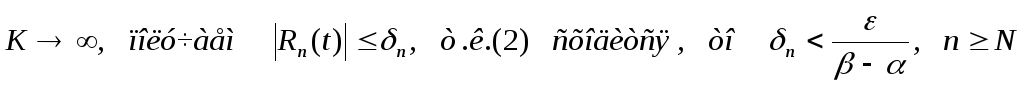
Теорема№3(о почленном дифференцировании функционального ряда):

Доказательство:

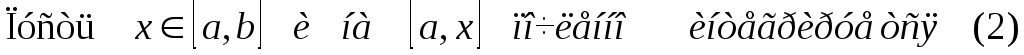
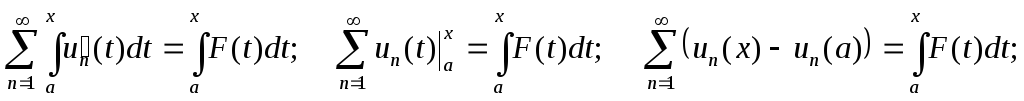
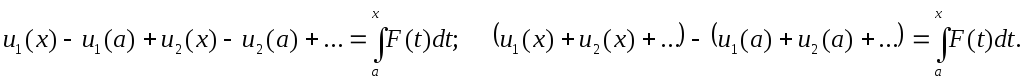
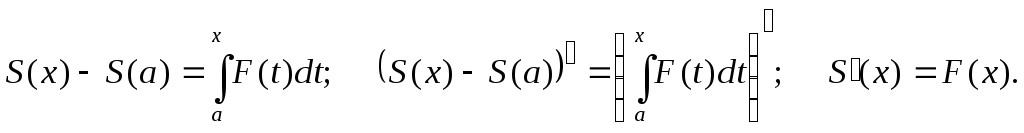
Степенные ряды(это обобщение многочлена)

Теорема(Абеля):

1)Пусть ряд (1) сходится при

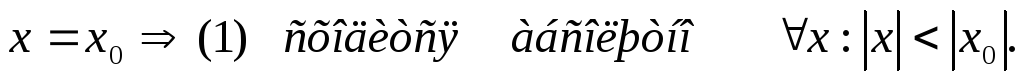
2)Пусть ряд (1) расходится или сходится условно при

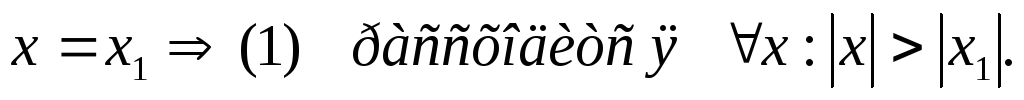
Доказательство:

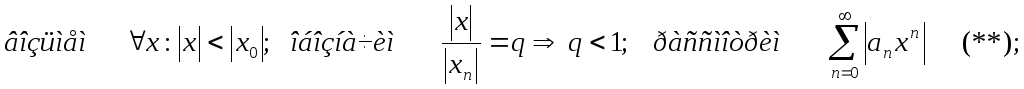
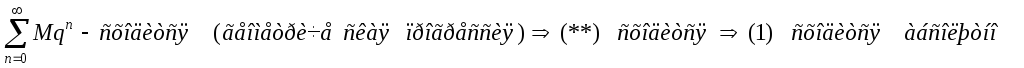
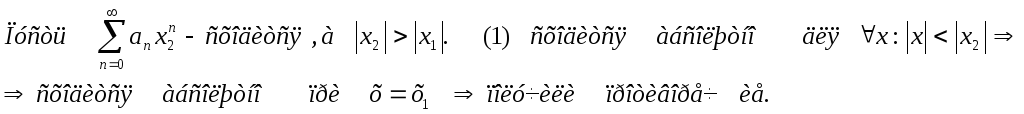
Теорема доказана.

Пусть А – множество точек сходимости ряда

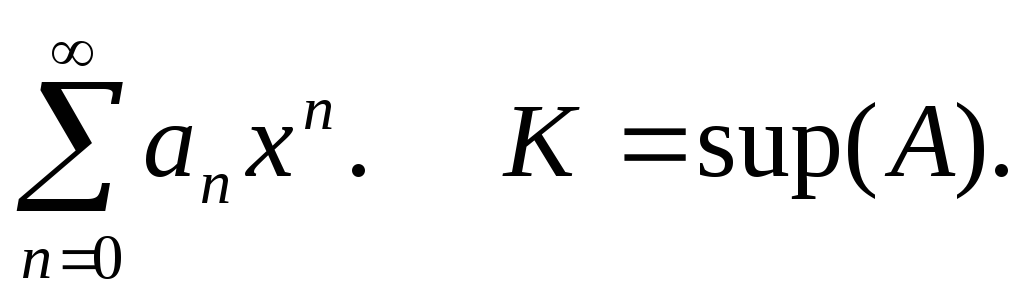
Supremum – точная верхняя грань; infinum – точная нижняя грань.

Если К>0 и ряд сходится абсолютно на (-К,К); если x<-K и x>K, то ряд расходится.

Если К=бесконечности, то ряд сходится абсолютно на всем числовой оси.

Если Л=0, то ряд сходится только при x=0.

Интервал сходимости степенного ряда

Исследуем абсолютную сходимость

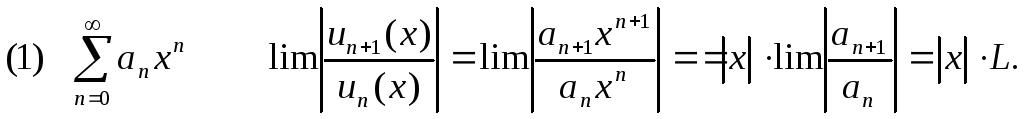
(конец первой темы)

Обобщенный степенной ряд.

(1) (-R,R)

R=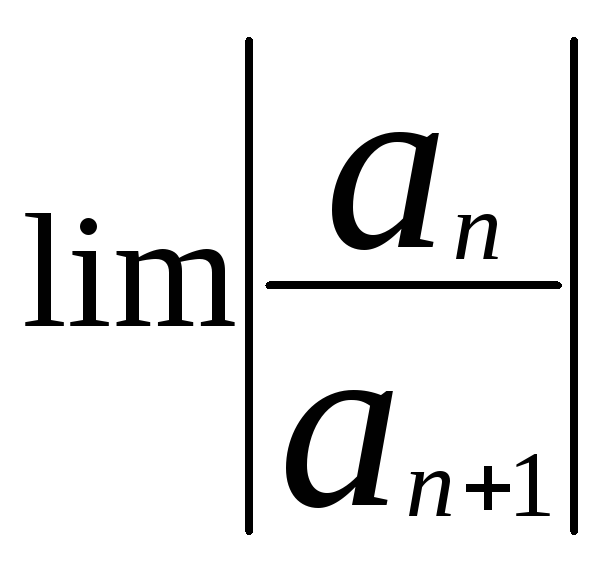

(2)

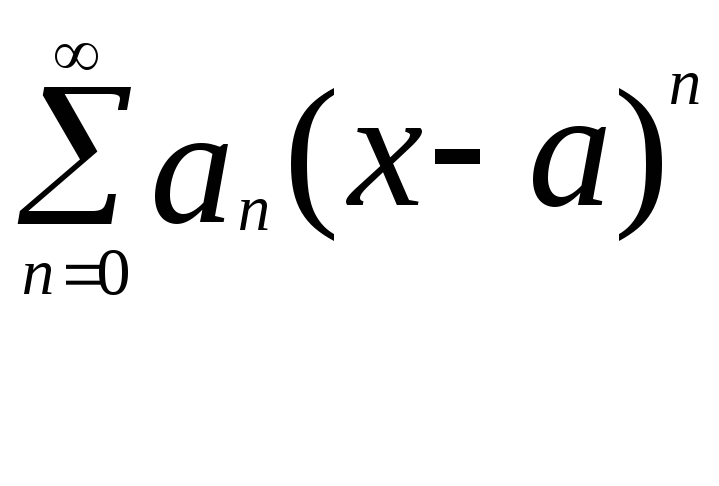
x-a=t

R=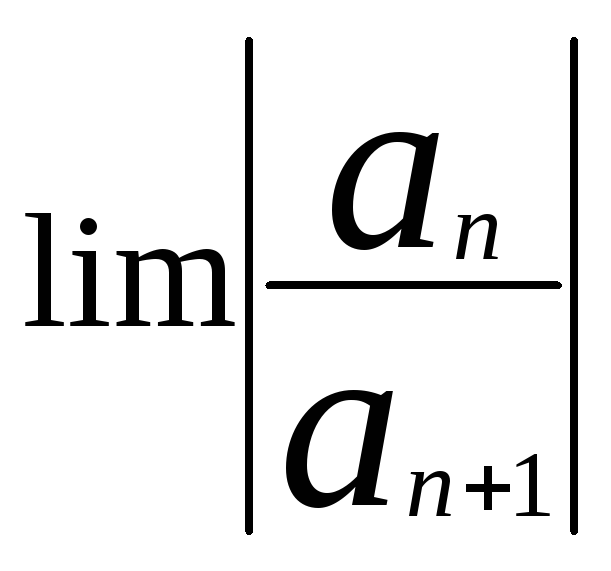

- |x-a| <R- > сходится абсолютно

- R<x-a<R- // -

a-R<x<a+R-> сходится абсолютно

x<a-R,x>a+R-> расходится

a-R a a+R

1) 2(x-1) -

R= lim || =

|x-1| <

- интервал сходимости.

- > сходится

область сходимости

2)

R=lim1 = 1 (-1,1) – интервал сходимости.

x=1 1+1+….. -> расходится

x= -1 1-1+….. ->сходится

(-1,1) – область сходимости

3) - > интервал сходимости и область сходимости

R= 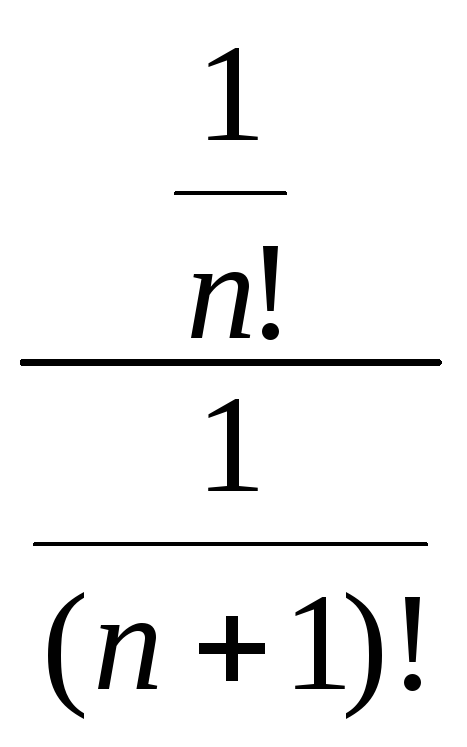=n+1 =

4)

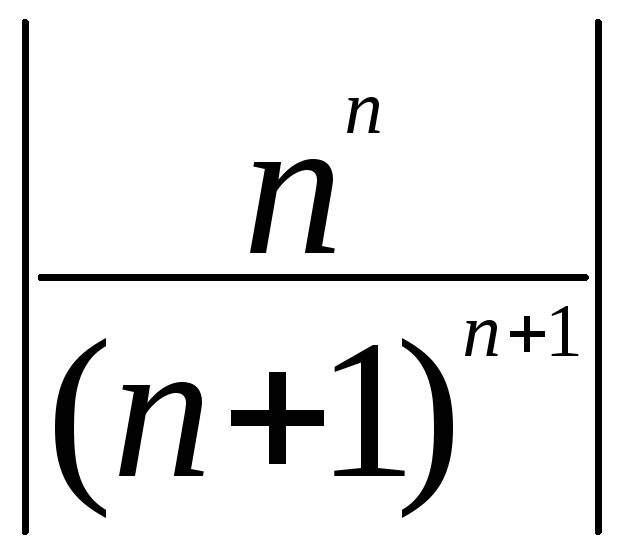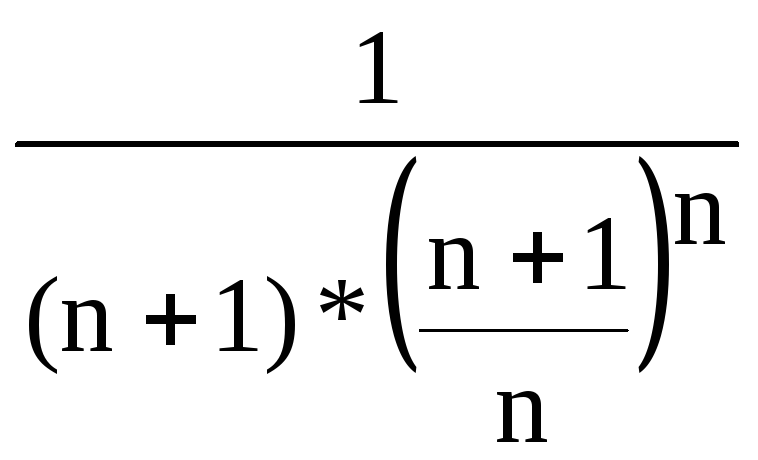R=== = 0

x=3 – область сходимости.