- •Производная функции.
- •Производные высших порядков.
- •2.Экстремумы.
- •3.Вогнутость.
- •4.Перегибы.
- •5.Ассимптоты.
- •Исследование функции
- •Неопределённый интеграл.
- •Геометрические приложения определенного интеграла
- •Повторный интеграл
- •Основные теоремы о степенных рядах.
- •Ряд Тейлора.
- •Разложение основных функций в ряд Тейлора.
- •Некоторые применения.
- •Числовые ряды комплексных чисел.
- •Степенные ряды комплексных чисел.
- •Периодичность.
- •П zоказательная функция.
- •Дост. Условия дифференцируемости.
- •Комплексно-значная формула комплексной переменной.
- •Правило обхода сложного контура.
- •Интеграл с переменным верхним пределом.
- •Интегральная формула Коши.
- •Решение неоднородного уравнения.
- •Метод вариации произвольных постоянных.
- •Решение неоднородного линейного уравнения с постоянными коэффициентами, где правая часть имеет специальный вид.
- •Метод вариации произвольных постоянных.
- •Основная теорема о вычетах
- •Вычисление вычетов в приложении к несобственным интегралам
- •Лемма Жордана
- •Решение дифференциальных уравнений.
- •Свертка функций.
Производные высших порядков.
z =z(x,y)
=z(x,y)
![]() - ?
- ? ![]() ,
,
![]()
![]()

![]() -
?
-
?
![]() yx
,
yx
,
![]() y2
y2
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
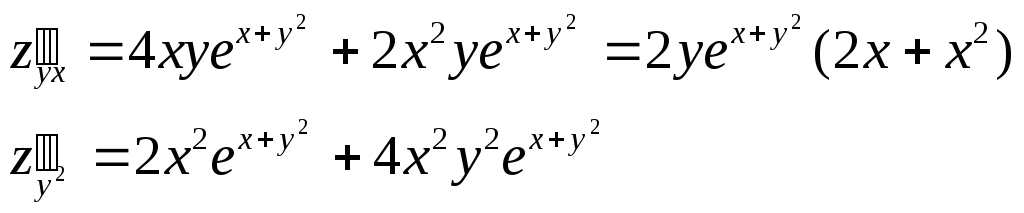
![]()
Теорема.
![]() непрерывна в
непрерывна в
![]() .
.
![]() ,
,![]() ,
,![]() ,
,![]() непрерывны в
непрерывны в
![]() .
.
Доказать:
![]()
![]()
![]()
![]() .
.
Доказательство:
![]()
![]()
![]()
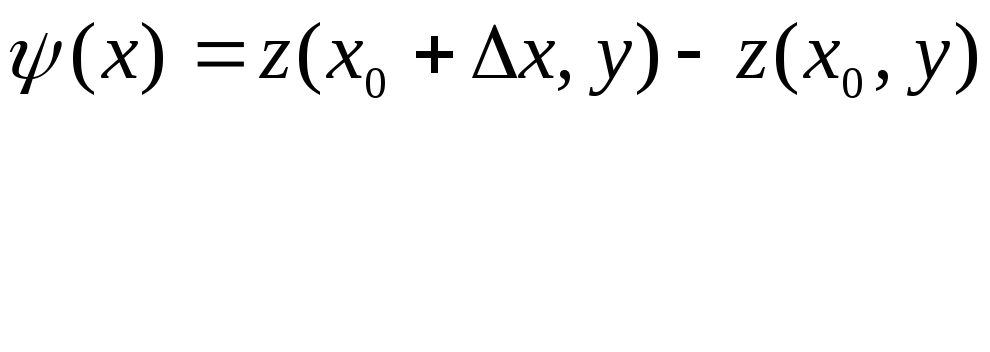
![]()
![]()


![]() =
=![]()
![]()

![]()
![]()
![]()
![]()
![]()

![]()
Скалярное поле.
![]()
![]()
![]()
![]() - поверхность
уровня.
- поверхность
уровня.
![]() - линия уровня.
- линия уровня.
Производная по направлению.
![]() непрерывна.
непрерывна.
![]() непрерывны.
непрерывны.
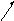
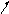
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
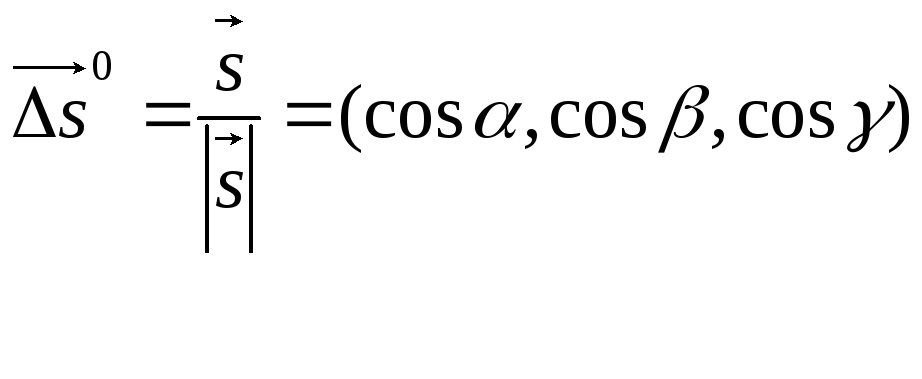






![]() ;
;
![]() ;
;![]()
![]()
![]()
![]()
Определение.
Производной U по направлению s называется:
|
|
![]()
![]()
![]()
![]()
![]()
![]()
Свойства производной по направлению.
Частные производные являются частным случаем производной по направлению.
![]()
![]()
![]()
![]()
![]()
2.
![]()
3.
![]()
Производная по направлению показывает скорость изменения функции в данном направлении.
![]()
![]()
Градиент показывает направление максимального изменения.
4. В каждой точке пространства градиент перпендикулярен поверхности уровня.
![]() -
скалярное поле.
-
скалярное поле.
![]() -
линия уровня.
-
линия уровня.
![]()
![]()
![]()
![]()
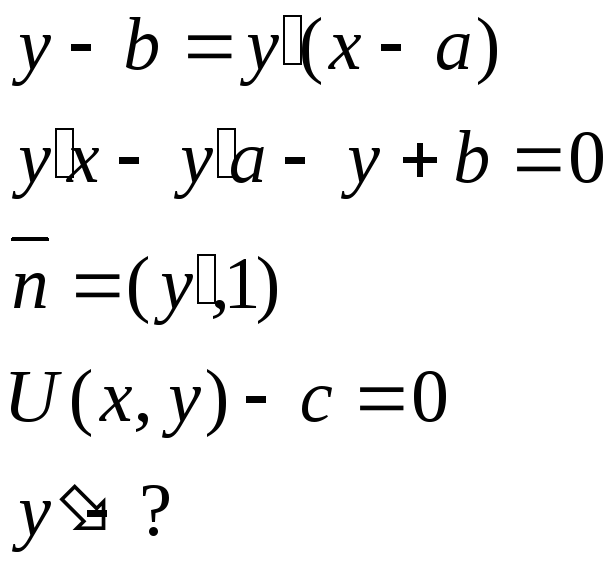
![]()
![]()
![]()
![]() ||
||![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Вектор-функция скалярного аргумента.
(1)
![]()
![]()
(2)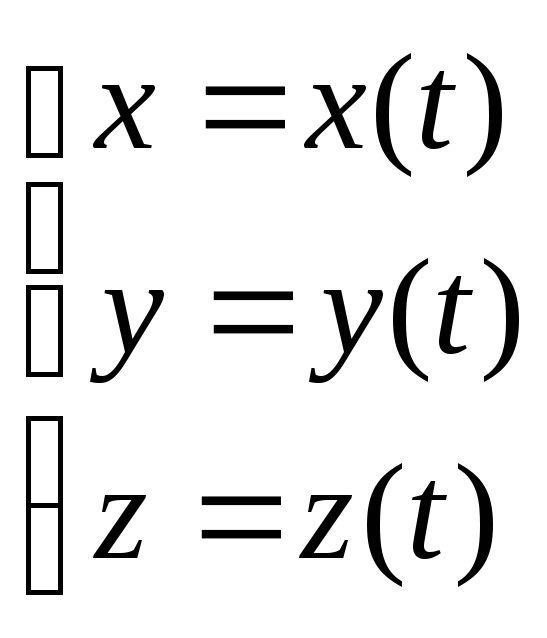
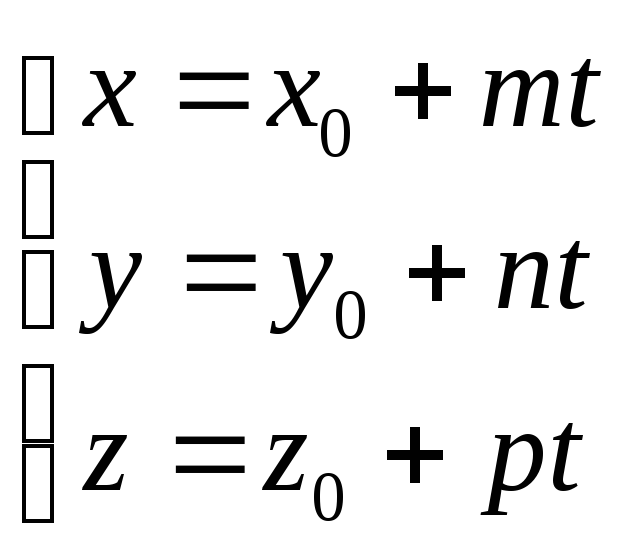
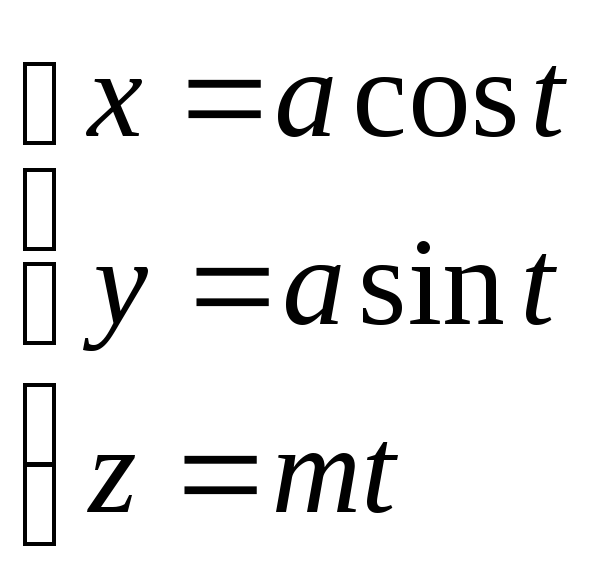 - винтовая линия.
- винтовая линия.
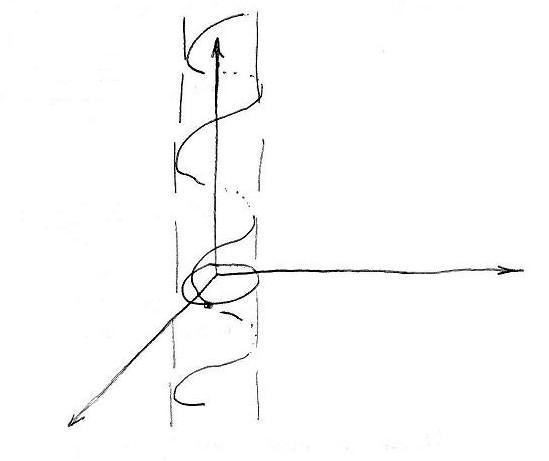
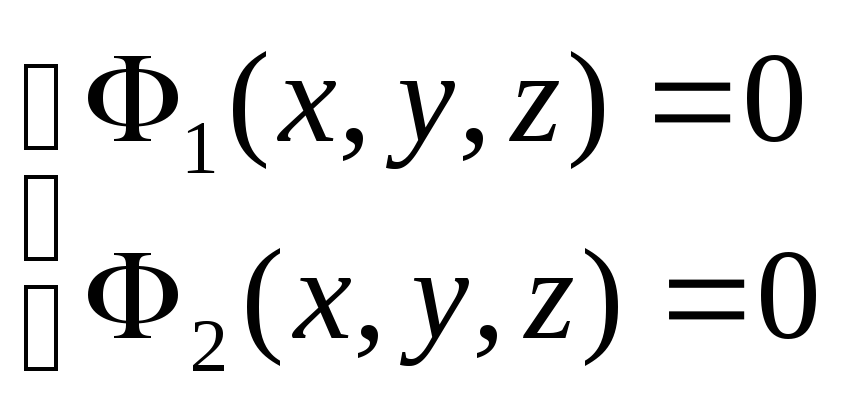
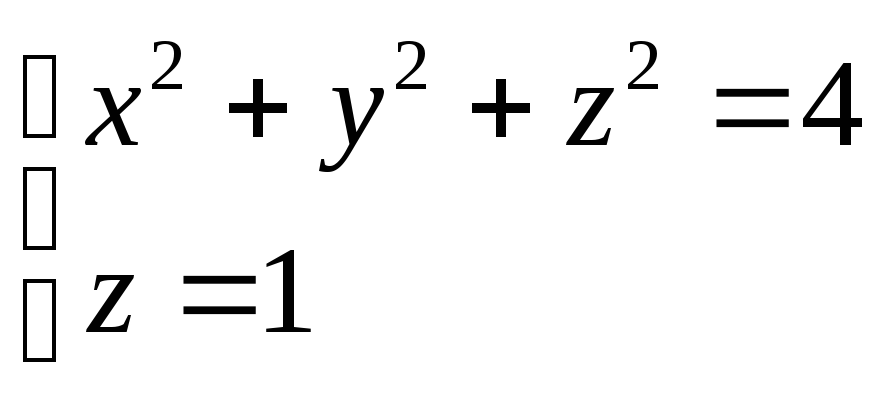 - окружность.
- окружность.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
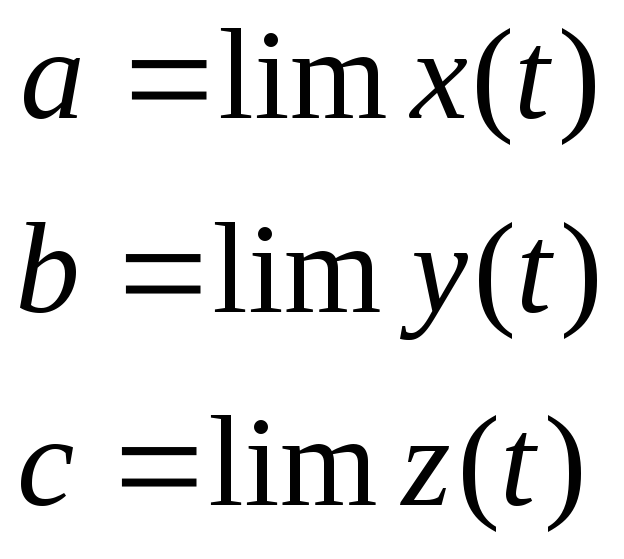
![]()
![]()
![]()
![]()
Производная вектора-функции.
![]()

![]()
![]() ||
||![]()
![]() направлен
по касательной.
направлен
по касательной.
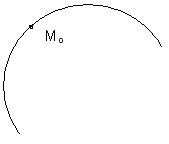
Уравнение касательной в пространстве.

![]() l
l
![]()
![]()
M0
– не особая
точка l,
т.е.
![]()
![]()
![]() -уравнение
касательной.
-уравнение
касательной.
Поверхность в пространстве.
![]() -
явное
уравнение поверхности.
-
явное
уравнение поверхности.
![]() -
неявное уравнение поверхности.
-
неявное уравнение поверхности.
![]()
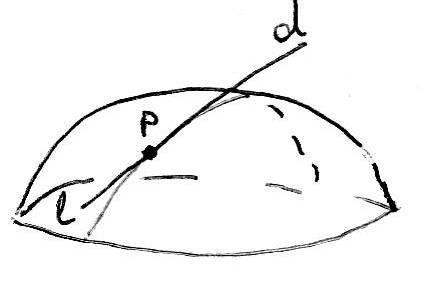
Касательная к поверхности – прямая, которая касается какой-либо кривой на поверхности.
Теорема.
![]() (поверхность
(поверхность
![]() )
)
P-
не особая точка поверхности
![]() ,
т . е.
,
т . е.![]()
Доказать:
все касательные, проходящие через точку P, лежат в одной плоскости.
Доказательство:
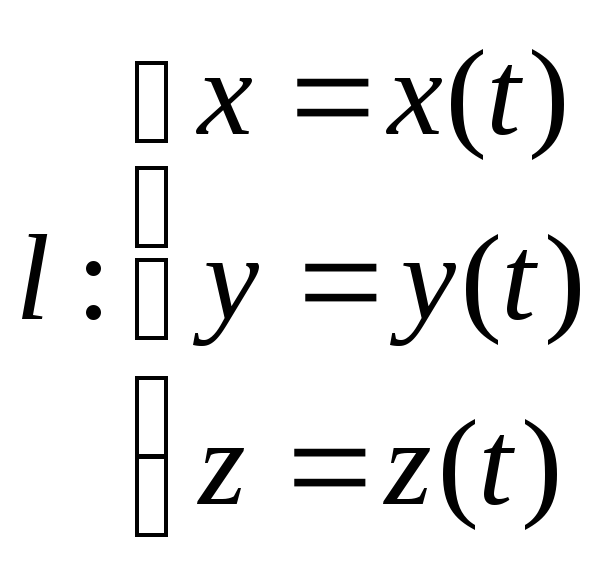
![]()
![]()
![]()
![]()
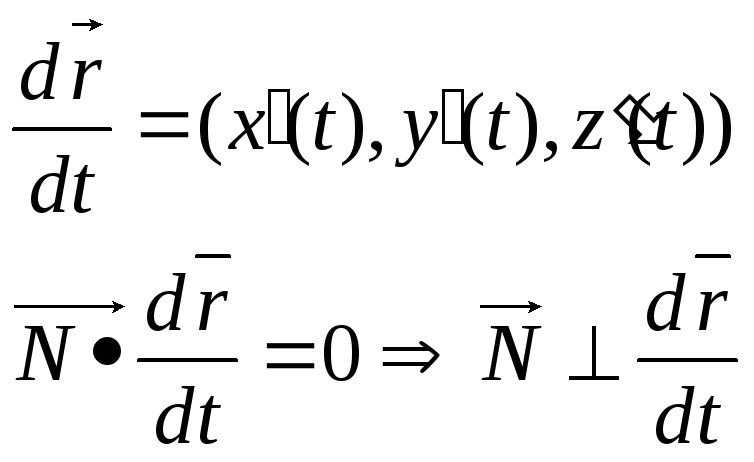
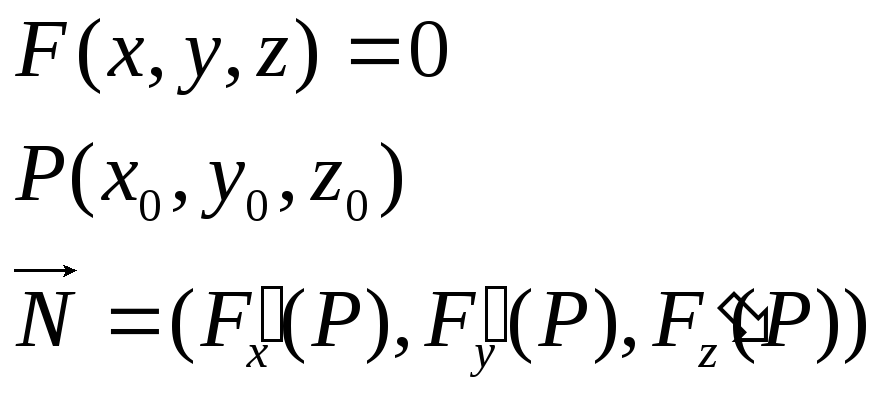
![]() -
уравнение касательной к плоскости.
-
уравнение касательной к плоскости.
![]() -
нормаль.
-
нормаль.
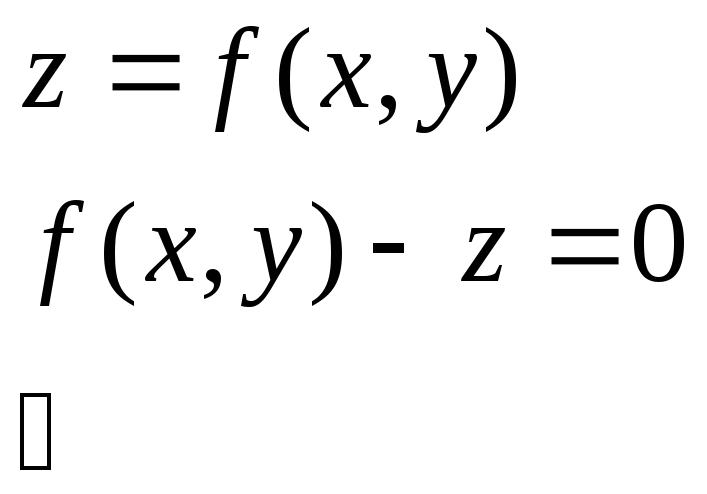
![]()
![]()
![]()
![]()
(![]() )
)![]() P(1,2,3)
P(1,2,3)
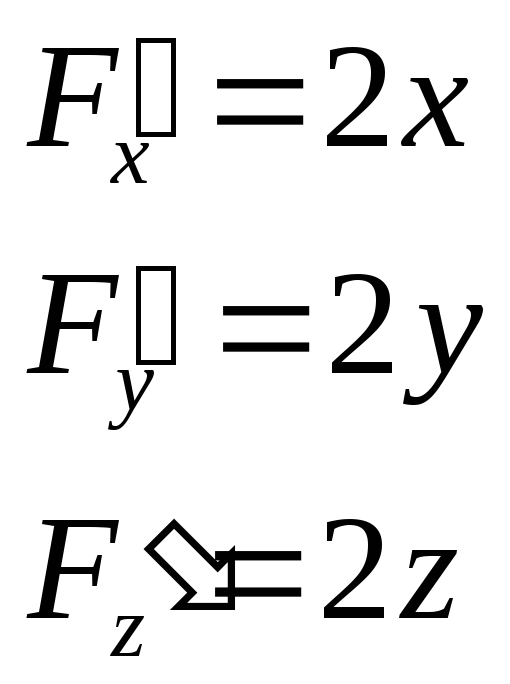
![]()
![]()
![]()
Экстремумы функции нескольких переменных.
![]()
![]() называется точкой
максимума
называется точкой
максимума
![]() ,
если в некоторойU(P)
выполняется
,
если в некоторойU(P)
выполняется
![]()
![]()
Теорема.(необходимое условие экстремума)
![]() непрерывна в
непрерывна в
![]()
существуют
![]() вP
вP
P- точка экстремума.
Доказать:
![]()
Доказательство:
![]() -
точка экстремума
-
точка экстремума
![]()
![]() -точка
экстремума
-точка
экстремума
![]()
![]() т. е.
т. е.
![]()
Аналогично
![]() .
.
Теорема(достаточное условие экстремума).
![]() непрерывна
в
непрерывна
в
![]()
имеет непрерывную частную производную до 3-го порядка
P-стационарная точка.
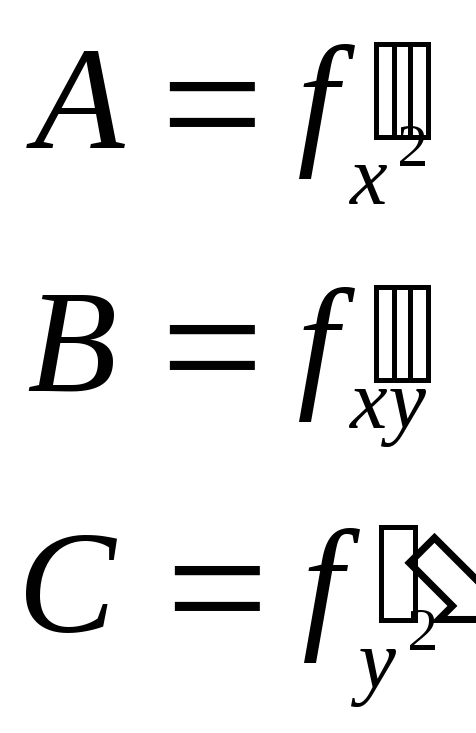
![]()
![]() -точка
экстремума, причем
-точка
экстремума, причем
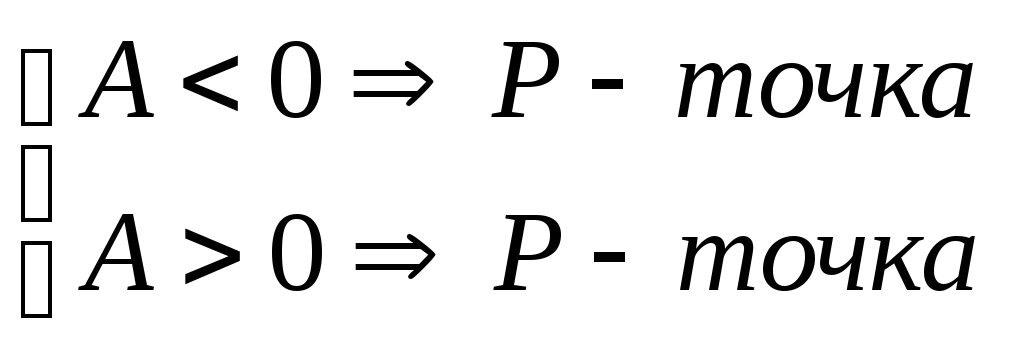
![]()
![]() нет
экстремума вP
нет
экстремума вP
Исследовать функцию на экстремумы:
![]()
![]()
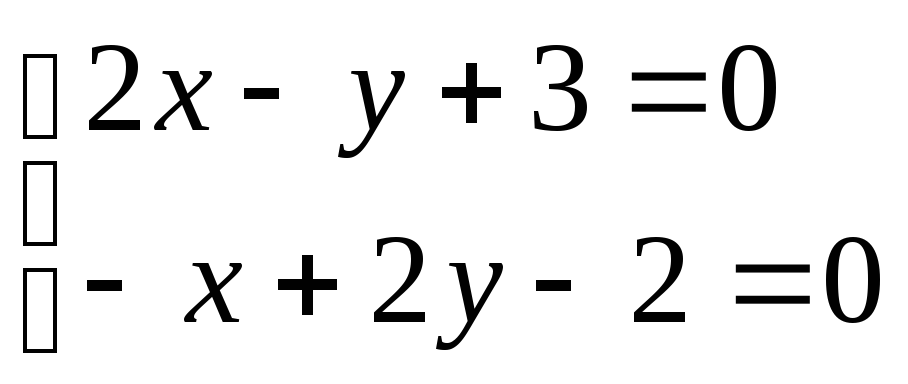
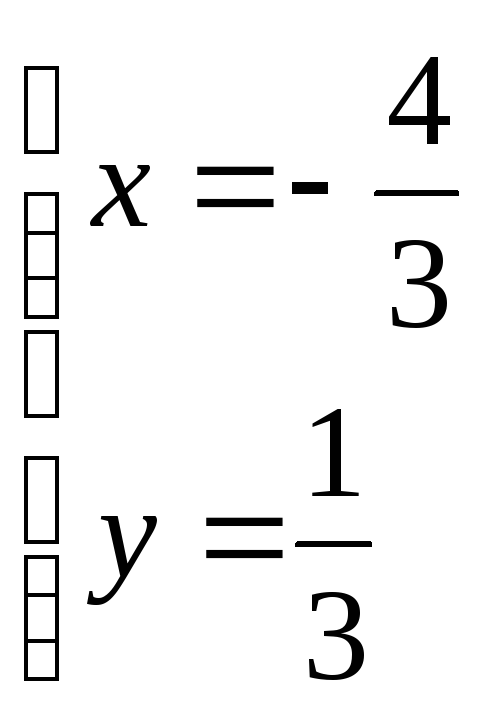
![]()
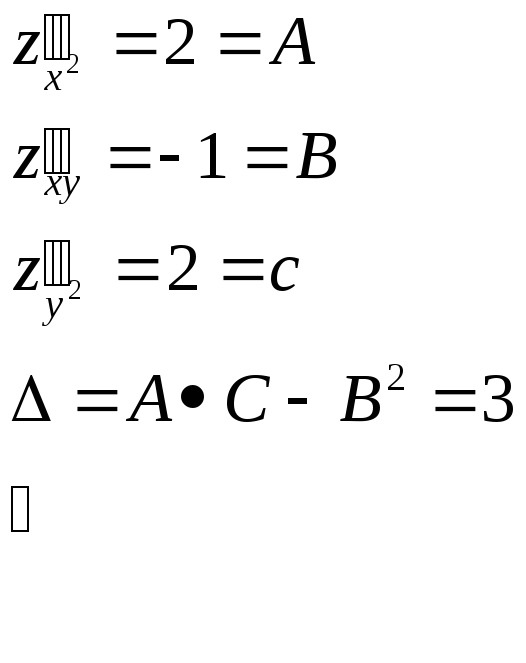
![]() -точка
минимума.
-точка
минимума.
2.Экстремумы.
О
0
x
0 0 0
Теорема 1(необх. усл. экстремума).
П
0
x
0 0
Док.
x
0 0 0
∆
0 0
∆
0
∆
0
0
0 0
Точки, в которых производная равна нулю, называются стационарными.
Точки, в которых производная равна нулю или имеет разрыв, называются критическими точками функции.
Теорема 2(дост. усл. экстремума).
y
0
![]()
x – критическая точка, если
0
0
0
0
Док.
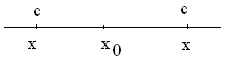
1
0 0 0
2
0 0 0 0
Теорема 3(Исследование на экстремум с помощью второй производной).
y
0
f
0 0 0 0
Док.
f
0 0
f ́(x)=>x ↓ - точка максимума