Решение неоднородного уравнения.

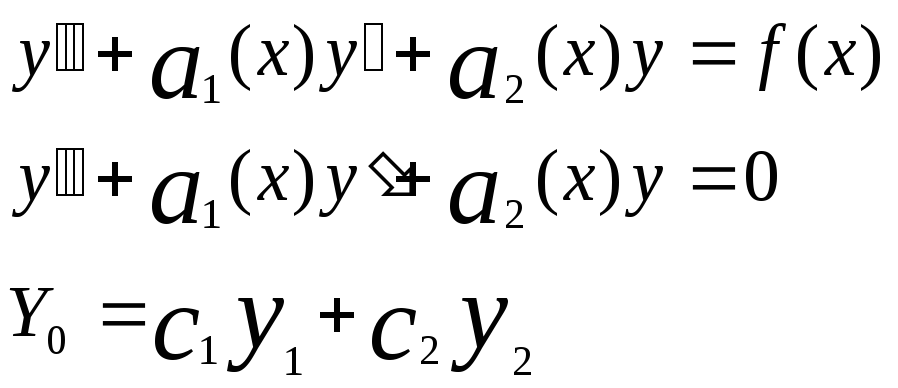(1)

(2)

- общее решение (2)

Метод вариации произвольных постоянных.

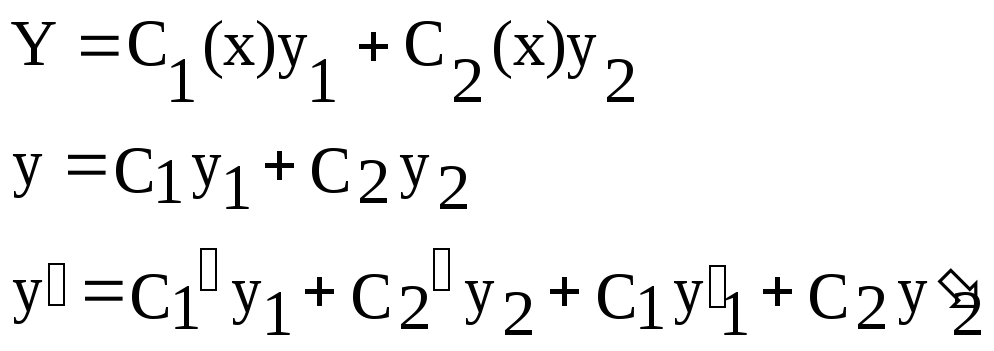
- решение (1) ищем в этом виде.

Пусть =0 ->

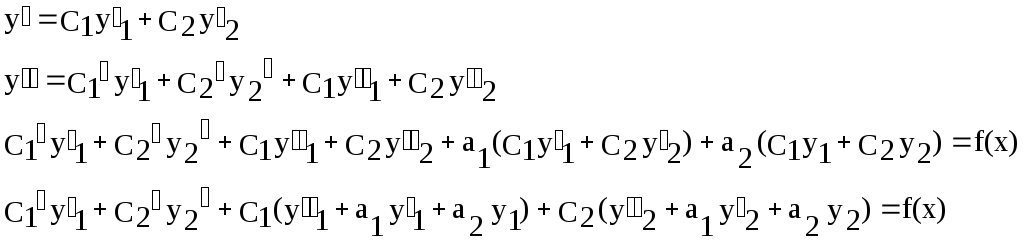
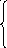
=f(x)

(3) -> единственное решение.

= 0

y1y2

=W(y1,y2)0

В общем виде:

Пусть - общее решение,

Тогда - общее решение,

где

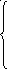
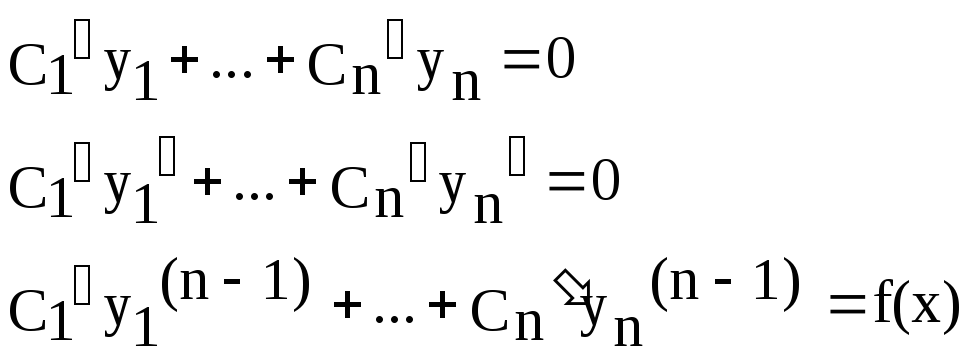(3)

Пример 1.

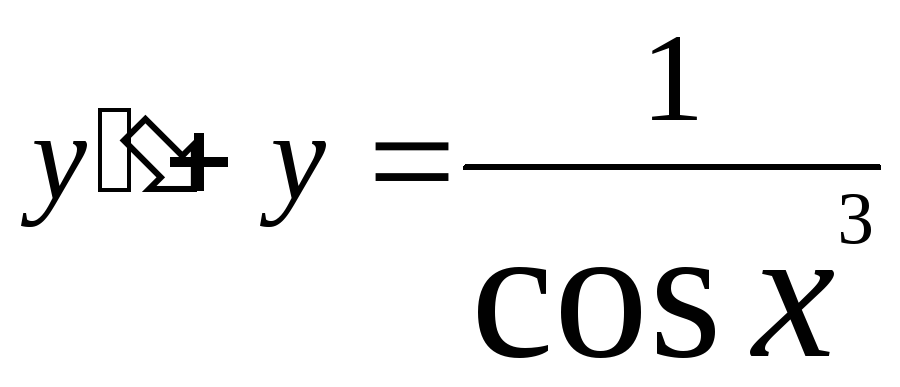
Решение.

1) = 0;

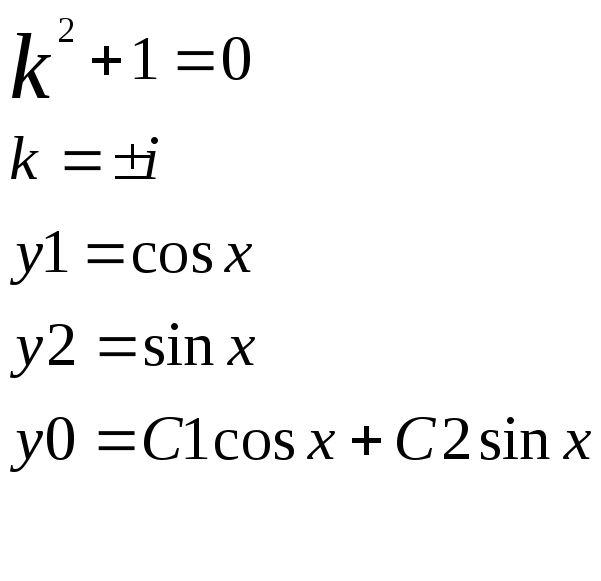
2) y =C1(x)cos x + C2(x) sin x

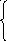
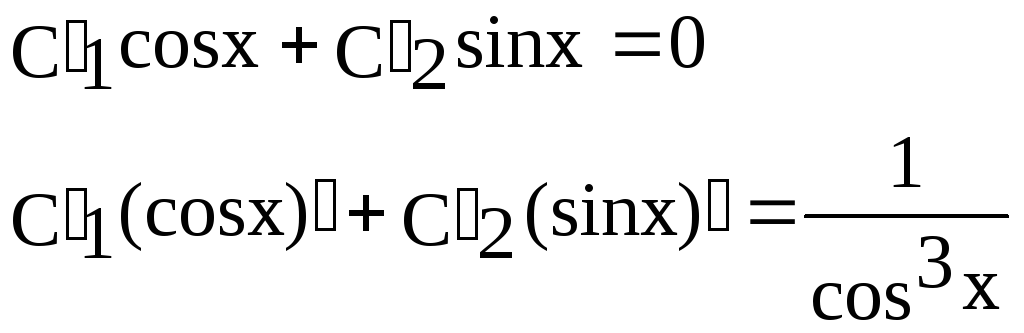
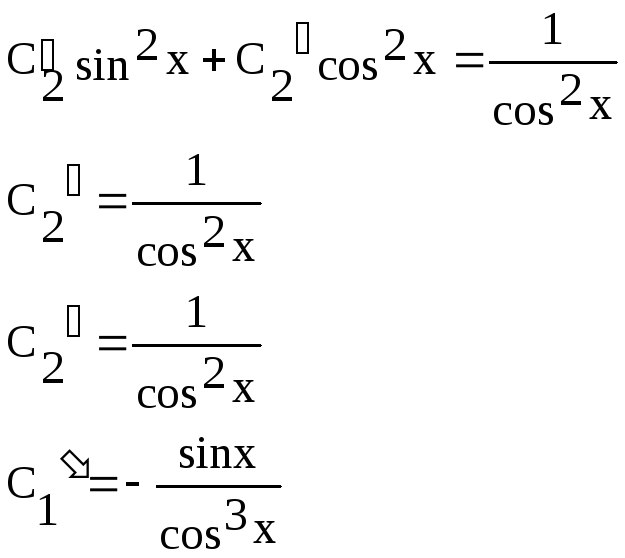
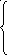
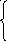
y = cos x + sin x + (cos x + tg x sin x).

Ответ. y = cos x + sin x + (cos x + tg x sin x).

Решение неоднородного линейного уравнения с постоянными коэффициентами, где правая часть имеет специальный вид.

(1)

(2)

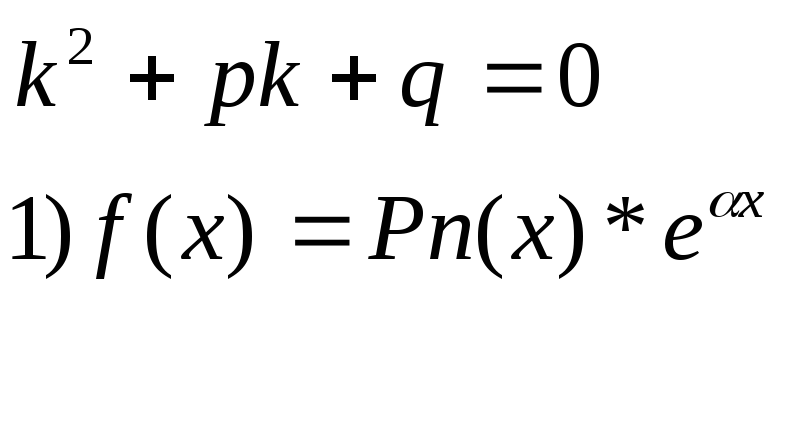(3)

I.не корень характеристического уравнения.

ищем в виде:

тогда

(*)

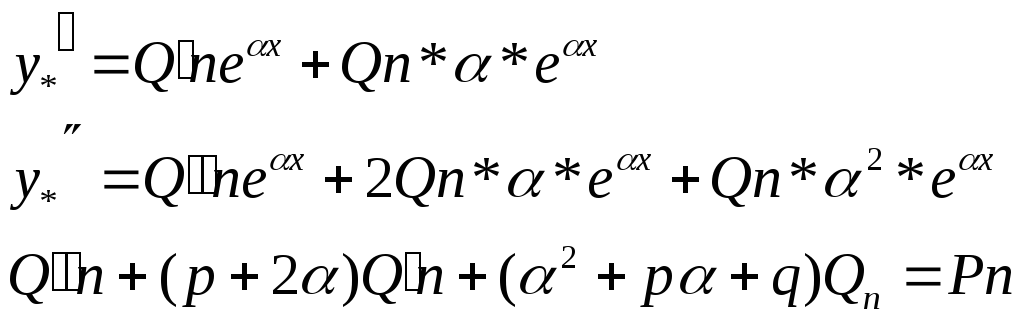
II.или,k1k2

ищем в виде:

(**)

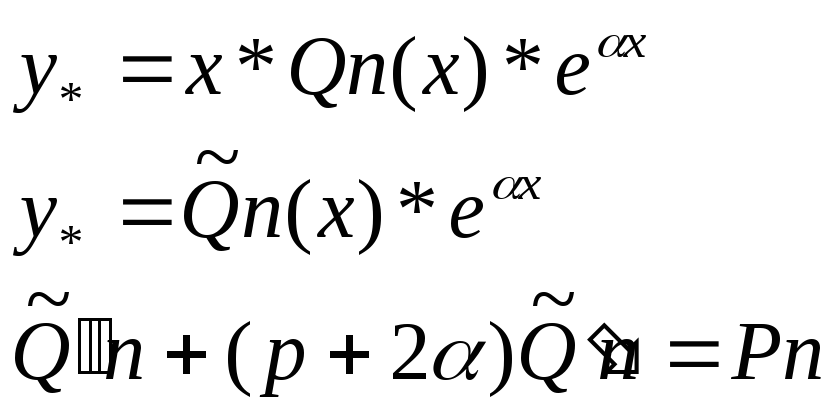
Ш. =k2=-p/2

ищем в виде:

(***)

2) f(x)=(Pn(x)cosx+Qn(x)sinx)n- старшая из степеней.

I. +i

= (Un(x) cosx + Vn(x)sinx)

II. +i

=x* (Un(x) cosx + Vn(x)sinx)

Пример 2.

Решение.

1)

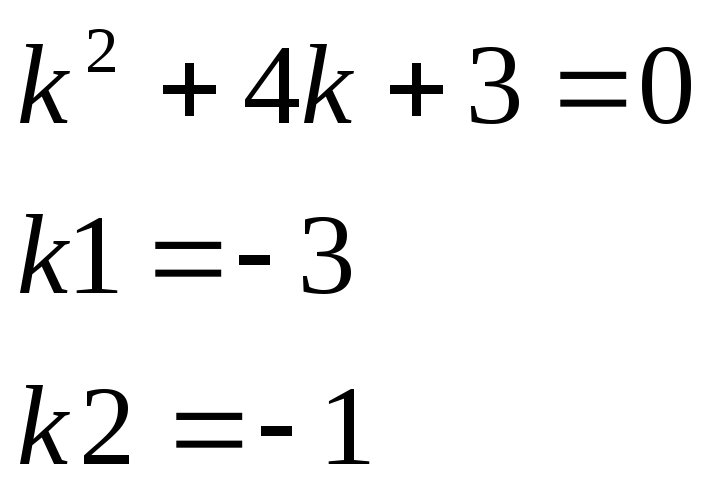
2)

Ответ. .

Пример 3.

Решение.

1)

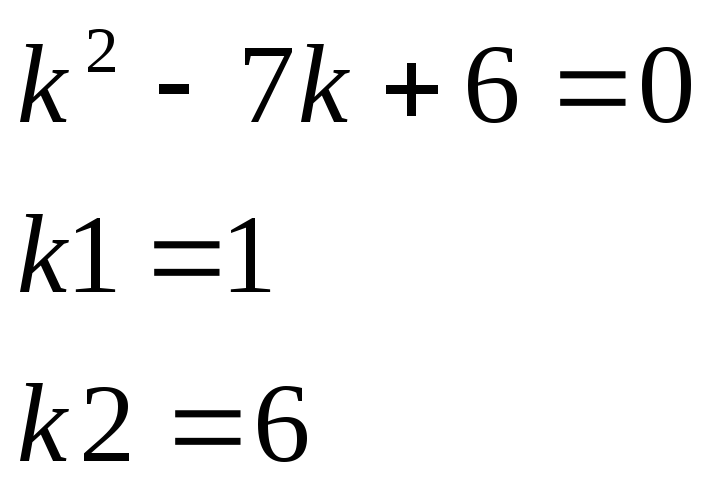
2)

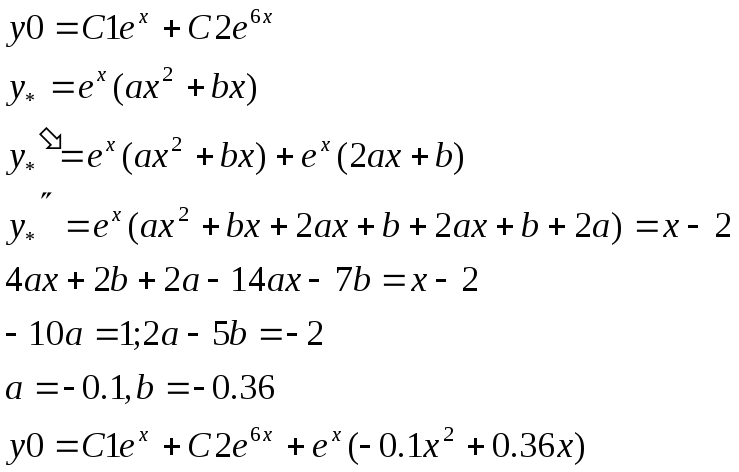
Ответ.

Пример 4.

Решение.

1)

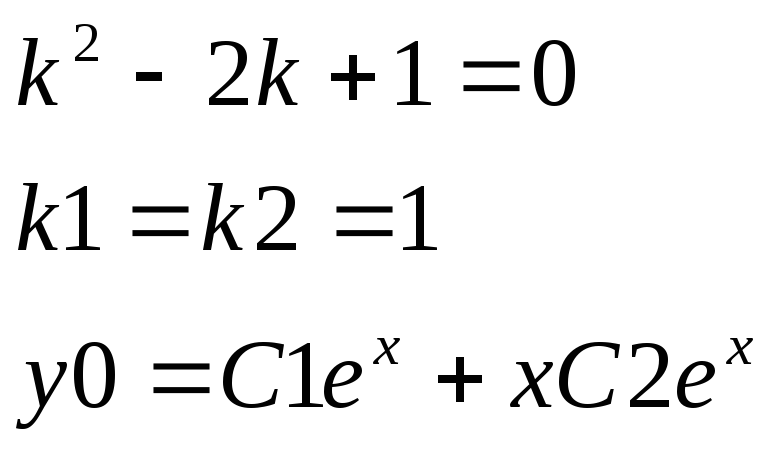
2)

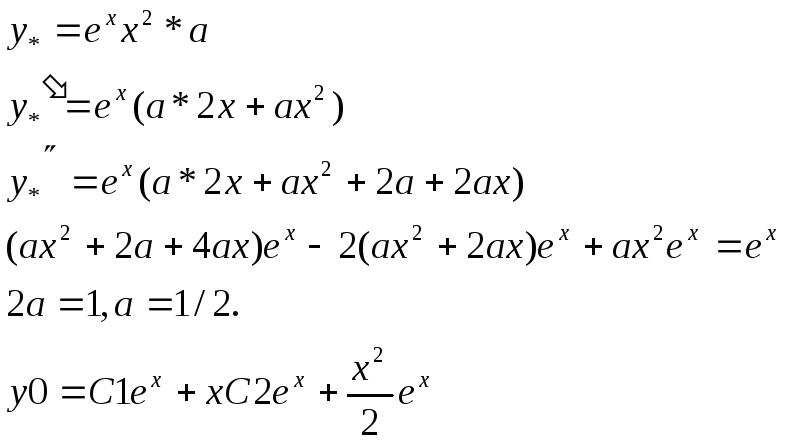
Ответ. .

Пример 5.

1)

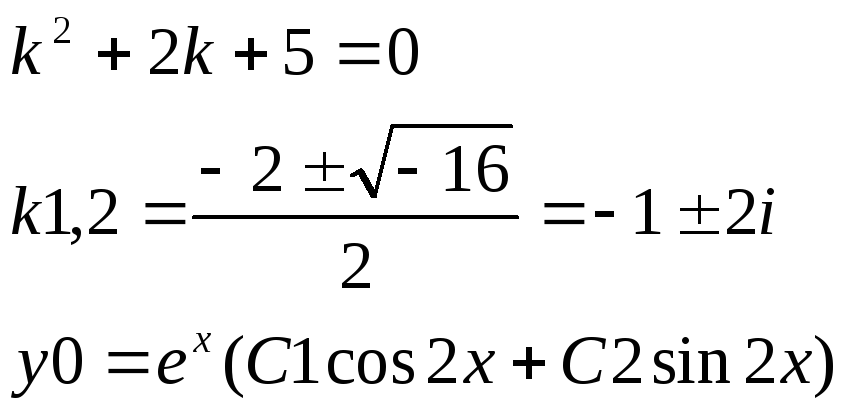
2)

=A cos x+ B sin x

=-A sin x+ B cos x

=-Acos x – B sin x

-Acos x – Bsin x – 2Asin x + 2Bcos x+5Acos x +5Bsin x = 2cos x

cos x(-A+2B+5A)=2cos x +sin x (B+2A-5B)

-A+2B+5A=2

4A+2B=2

2A+2B=1

B=1/5, A=2/5;

y = 2/5 cos x +1/5 sin x

y =

Ответ. y=.

Пример 6.

1)

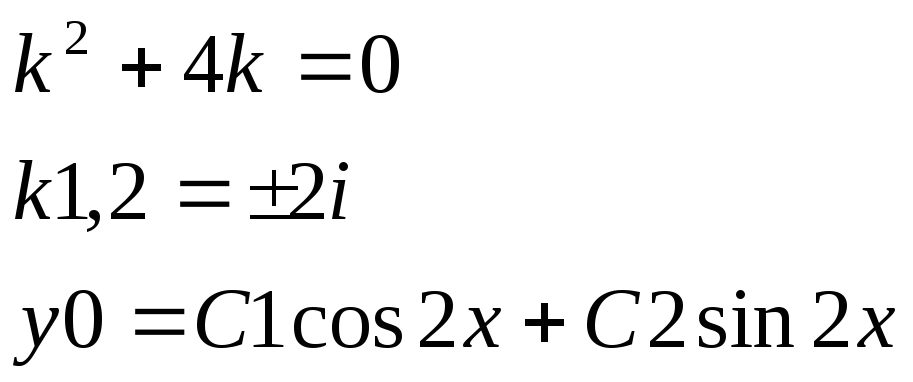
2)

=x (Acos 2x + Bsin 2x)

=(-2Asin 2x+2Bcos 2x)x + Acos 2x+ Bsin 2x

= - 2Asin 2x + 2Bcos 2x + x(-4Acos 2x – 4Bsin 2x) + Acos 2x +Bsin 2x.

-2Asin 2x+ 2B cos 2x + Acos 2x + Bsin 2x = 0

(-2A+B)sin 2x + (2B+A)cos 2x=0.

A=0, B=1/4;

=x(1/4 sin 2x).

Y=C1cos 2x + C2 sin 2x+ ¼*x*sin 2x.

Ответ. Y=C1cos 2x + C2 sin 2x+ ¼*x*sin 2x.

Теорема 8.

решение

решение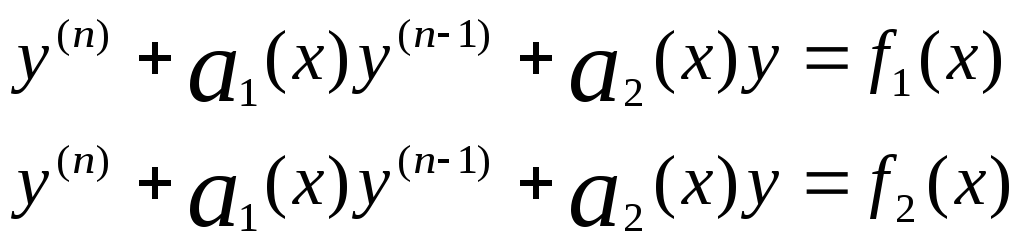

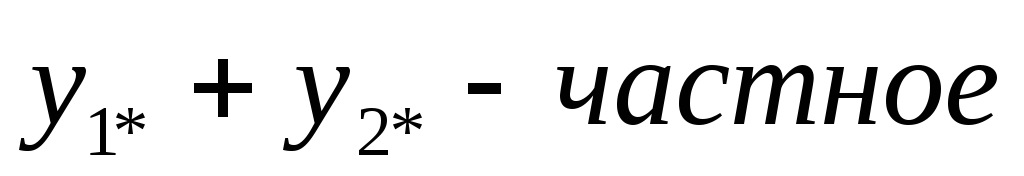решение уравнения+

Доказательство.

Проверим:

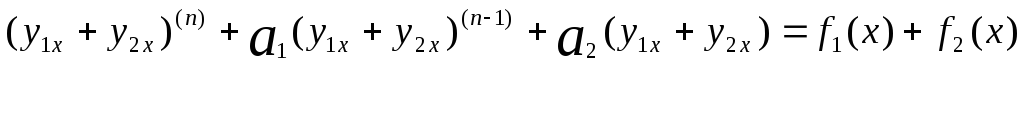
ч.т.д.

Пример 7.

Решение.

1)

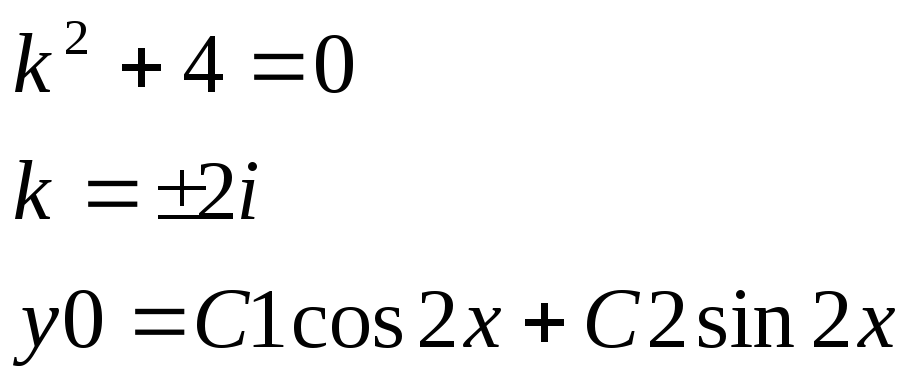
2)

f1(x) = x , =Ax+B

f2(x) = 3

(A+ C)` + 4 (Ax+B+C) = x + 3

C+4Ax+4B+4C=x +3

C=3/5, A=1/4, B=0;

y=C1cos 2x + C2sin 2x + 1/4x+ 3/5

СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРОВНЕНИЙ.

(1)

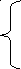
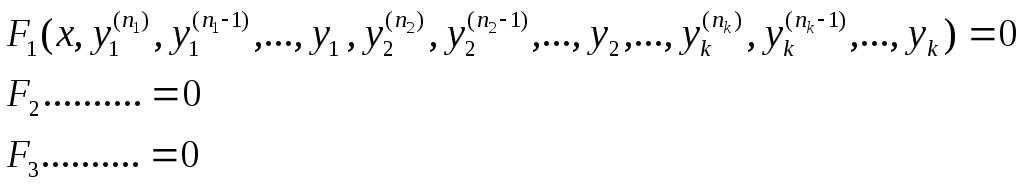
(2)

Т.1

Если система разрешена относительно старших производных, то можно свести к нормальному виду.

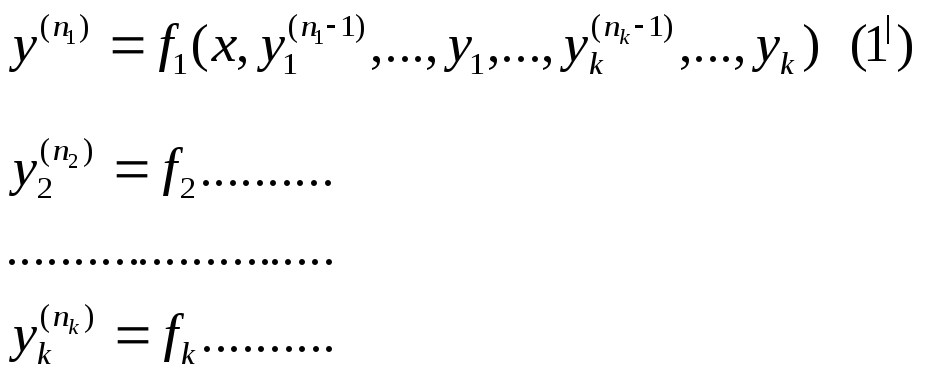
Док.

пусть y=y₁, y^|=y₂,…, y^(n-1)=y_n

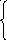
Сведение дифференциальных систем уравнений к линейным

;

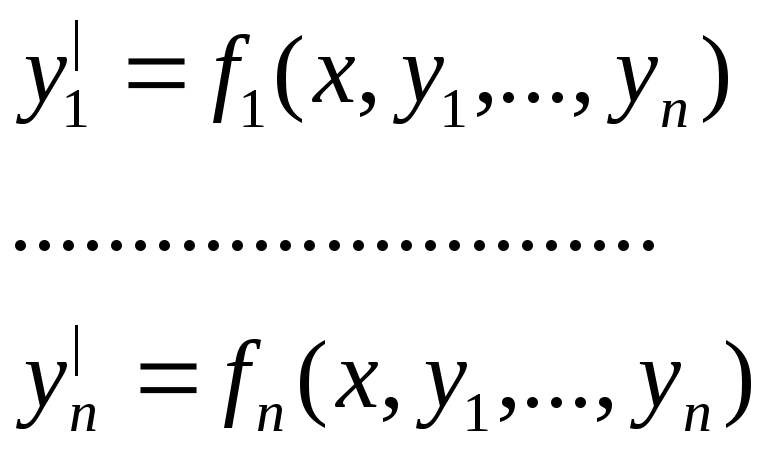
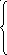
Аналогично

()

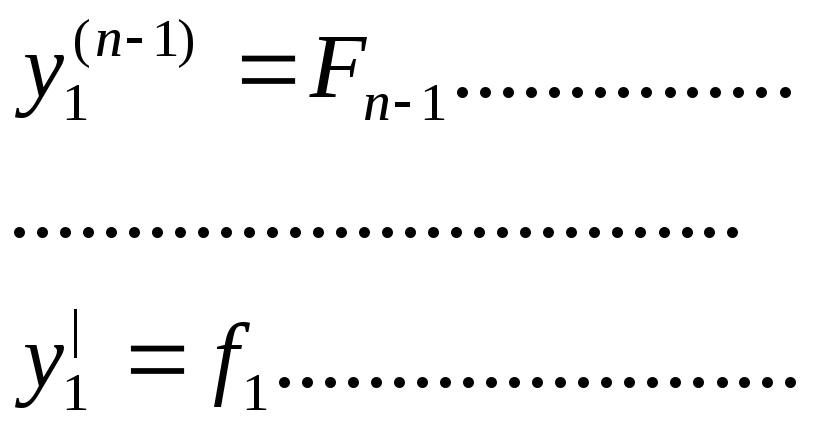решение относительно y₂,…,y_n

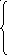
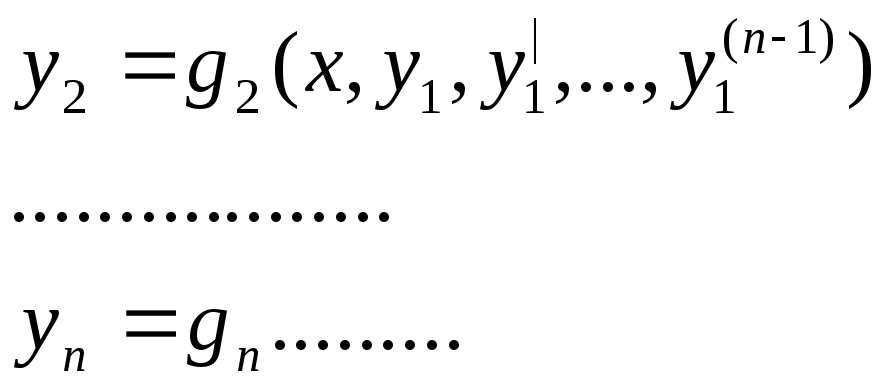
Подставим в ()

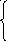
y^| = x+y+z

z^| = 2x-4y-3z

y(0)=0

z(0)=0

y^|| = 1+y^| +z^|

y^|| = 1+x+y+z+2x-4y-3z

z=y^| -x-y

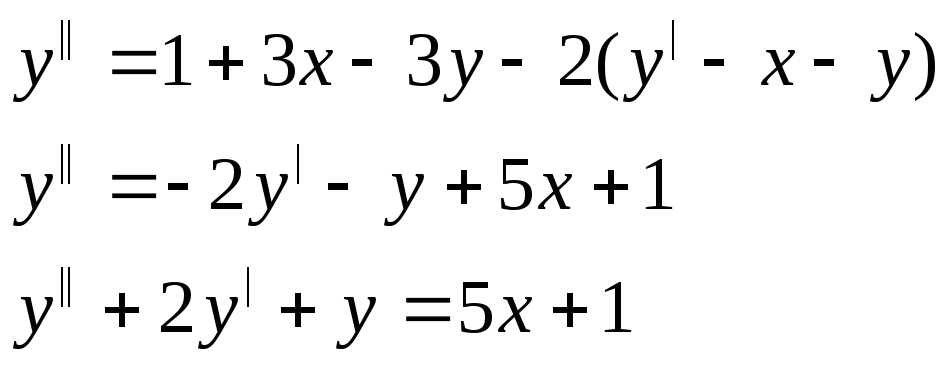
K=-1

y₀ =e^-x(c₁+c₂x)

2)

y_* Ax+B

2A+Ax+B = 5x+1

A=5

B=-9

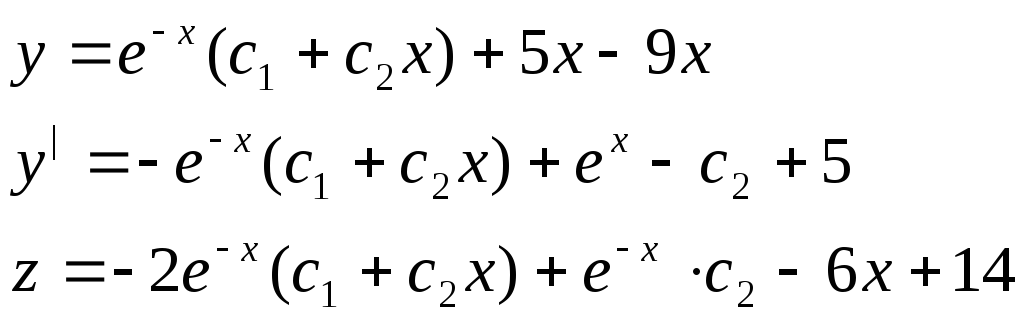
1=c₁-9 c₁=10

0=-2c₁+c₂+14 c₂=6

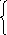
Линейные системы

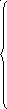
(1)

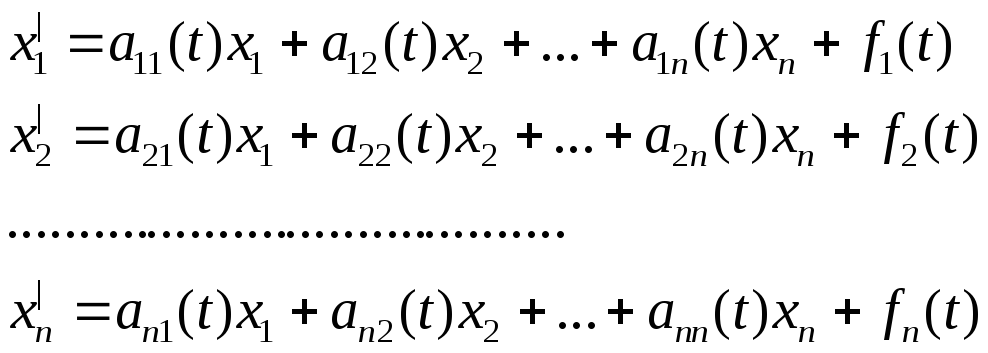
X=(x₁,…,x_n)

…

A(t)= …

…………………………

…

(1) (2)

Общее решение однородной системы

x¹,…,xⁿ – частные лин. Независимые решения (2)

С₁,…,С_n – произвольные постоянные

О.р. (1):

X=X⁰+X^*

X⁰- общее решение однородной системы

X^*- частные решения (1)

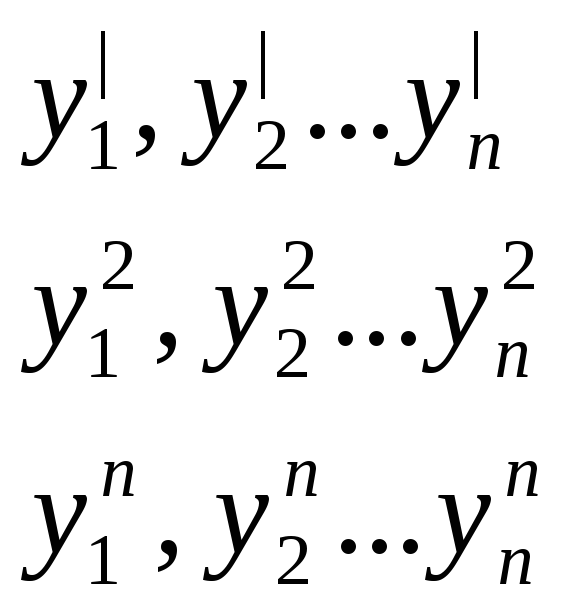
y^|,…,yⁿ – лин. Независимы =>

x^|,…,xⁿ – решение (2)

x^|,…,xⁿ лин. независимыW(x^|,…,xⁿ)

Линейные системы с постоянными коэффициентами

(1)

(2)

ищем решение (2) в виде

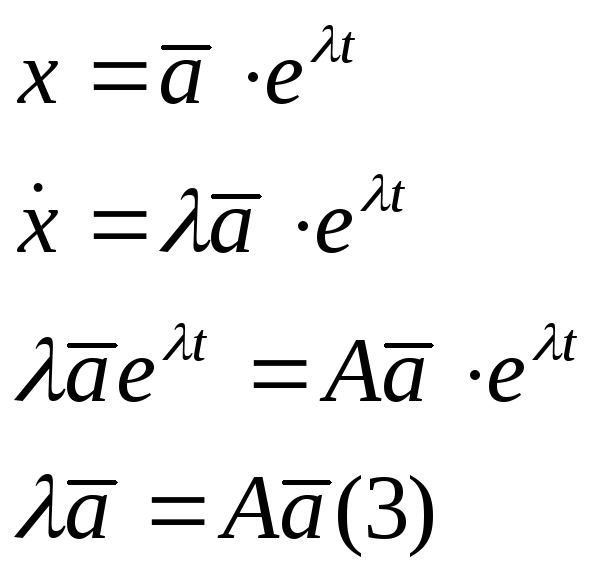
Если и выполняется (3), тоназывается собственным числом А

-собственным вектором

(4)

1) (4) имеет n корней

=> , j=1,…,n.

лин. независимые решения (2)

2) (4) имеет кратные корни.

Пусть - корень кратности

ему соответствуют собственные векторы

2.1) k=m

лин. независимые решения (2)

2.2) k<m

=> частное решение ищется в виде

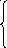
3 4 -2

A= 1 0 1

6 -6 5

-1- 4 -2

1 - 1

6 -6 5-

(-3-) ( -5 +6) -4(5--6) -2(-6+6)=0

-(+3)( ² -5 +6) +8 +16

(+3)( -2)( -3) +8(-2)=0

=2 ² -9 +8=0 =1