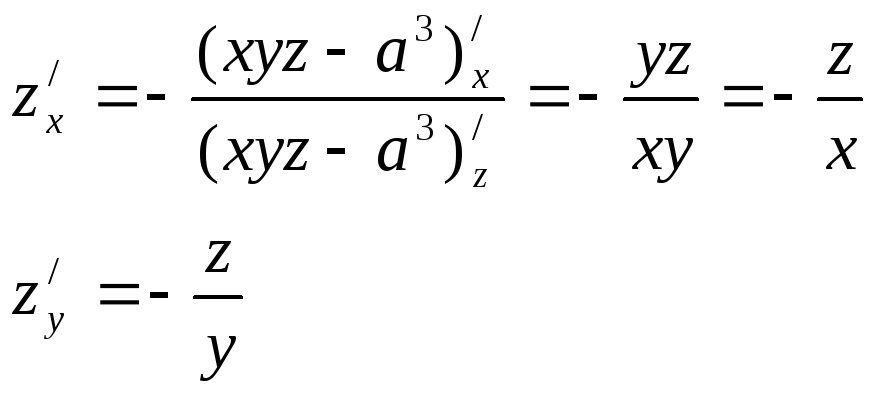- •Производная функции.
- •Производные высших порядков.
- •2.Экстремумы.
- •3.Вогнутость.
- •4.Перегибы.
- •5.Ассимптоты.
- •Исследование функции
- •Неопределённый интеграл.
- •Геометрические приложения определенного интеграла
- •Повторный интеграл
- •Основные теоремы о степенных рядах.
- •Ряд Тейлора.
- •Разложение основных функций в ряд Тейлора.
- •Некоторые применения.
- •Числовые ряды комплексных чисел.
- •Степенные ряды комплексных чисел.
- •Периодичность.
- •П zоказательная функция.
- •Дост. Условия дифференцируемости.
- •Комплексно-значная формула комплексной переменной.
- •Правило обхода сложного контура.
- •Интеграл с переменным верхним пределом.
- •Интегральная формула Коши.
- •Решение неоднородного уравнения.
- •Метод вариации произвольных постоянных.
- •Решение неоднородного линейного уравнения с постоянными коэффициентами, где правая часть имеет специальный вид.
- •Метод вариации произвольных постоянных.
- •Основная теорема о вычетах
- •Вычисление вычетов в приложении к несобственным интегралам
- •Лемма Жордана
- •Решение дифференциальных уравнений.
- •Свертка функций.
Числовые множества:
Z-мн. целых чисел n≠0;
Q-мн. рациональный чисел
Рациональные числа выражаются конечной и бесконечной периодической дробью, а все остальные числа называются иррациональной бесконечной непериодической дробью.

a<b то число которое левее всегда меньше числа которое правее
Свойства действительных чисел:
Между двумя действительными числами всегда находится рациональное и иррациональное.
Любое иррациональное число можно с любой степени точности заменить рациональным.
А,В – множество
![]() (a
вложено в B)
(a
вложено в B)
А={1,3,5,7}
B={1,2,3,4,5,6,7}
![]() пустое
подмножество любого множества
пустое
подмножество любого множества
N<Z<Q<R<C
[a,b]- отрезок
![]()
(а,b)- интервал
a<x<b
Окрестность точки – интервал с центром в этой точке

![]() r- радиус
окрестности
r- радиус
окрестности
Ur(a)- r окрестность точки а.
![]()
Ur0(a)- проколотая окрестность.
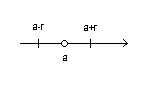
a-r<x<a+r , x≠a.
|a-x|<r , x≠a.
|a|=![]()
Окрестность- все числа а и b которые отдалены на расстояние r.
Свойства обсалютных величин:
1) |a+b|![]() |a|+|b|
|a|+|b|
Доказательство:
|a|=![]()
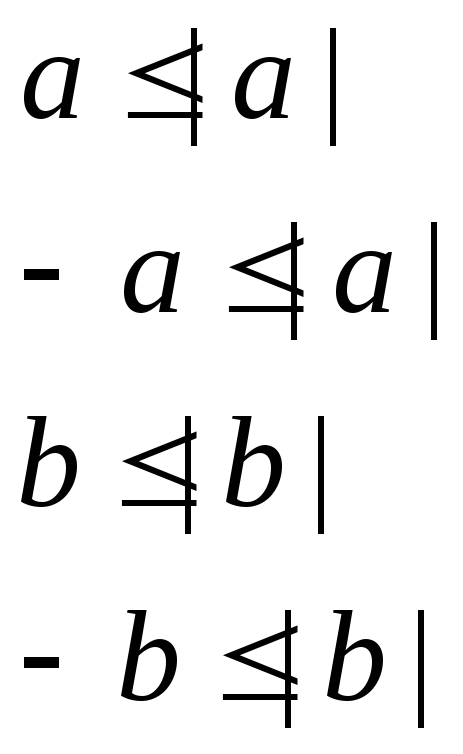
|a+b|![]() |a|+|b|
|a|+|b|
-(a+b)
![]() |a|+|b|
=> |a+b|
|a|+|b|
=> |a+b|![]() |a|+|b|
|a|+|b|
2) |a|-|b|![]() |a-b|
|a-b|
Доказательство:
Пусть a-b=c
a=b+c
|b+c|![]() |b|+|c|
|b|+|c|
|a|![]() |b|+|a-b|
|b|+|a-b|
|a|-|b|![]() |a-b|
|a-b|
|ab|=|a|*|b|

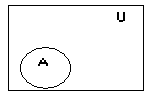
Операции над множествами
универсальное множество
А,В- подмножества U,
![]() пустое
множество
пустое
множество
Диаграмма Эйлера

![]() -
объединение
-
объединение
«ИЛИ»
![]()
![]()
![]()
![]()

«И»
![]()
![]() ,
и
,
и
![]() .
.
А -
дополнение(все элементы которой не
принадлежат А)
-
дополнение(все элементы которой не
принадлежат А)
«НЕ»
Свойство операций:
1)![]() 1)’
1)’
![]()
2)![]() 2)’
2)’![]()
3)![]() 3)’
3)’![]()
Законы Моргана
4)![]() 4)’
4)’![]()
5)![]() 5)’
5)’![]()
6)
![]() 6)’
6)’![]()
7)
![]() 7)’
7)’
![]()
8)

Отображения множеств
Кванторы
![]() -
всеобщность (всякий, любой).
-
всеобщность (всякий, любой).
![]() -
существования (существует, найдется).
-
существования (существует, найдется).
![]()
Любому элементу
множества А ставится в соответствии
единственный элемент из множества В.
Т.е.
![]() а
а![]() А→
единств.b
А→
единств.b![]() В.
В.
![]()
мн. А - область
определения функции
![]()
мн. В- множество значений функции.
Сложная функция:
если на мн. А определены функция
![]() ,
на В определена
функция q,
то на а
определяется функция a=g(f(a)).
,
на В определена
функция q,
то на а
определяется функция a=g(f(a)).
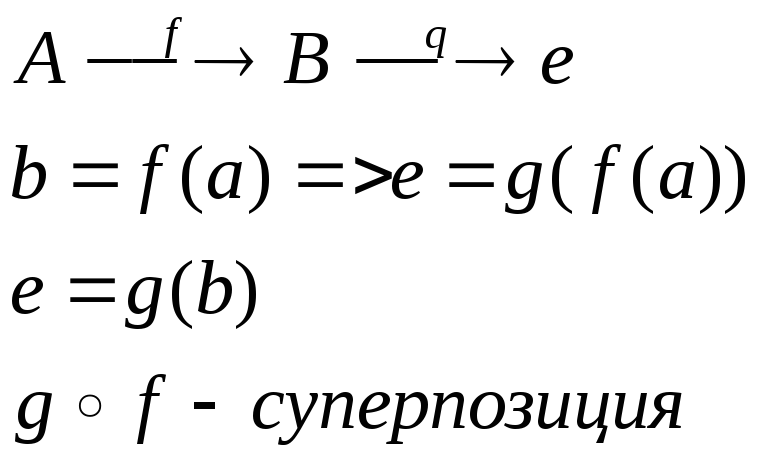
Отображение множителей

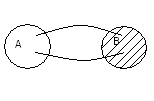
1.Отображением называется инъективным или просто инъекция.
![]() -
инъекция,
если разным прообразам соответствуют
разные образы.
-
инъекция,
если разным прообразам соответствуют
разные образы.

2.
![]() -
сюрьективным,
сюрьеция, если множество образов A
совпадает со множеством В.
-
сюрьективным,
сюрьеция, если множество образов A
совпадает со множеством В.
![]() b
b![]() B
B
![]() a
a
![]() A : f(a)=b
A : f(a)=b

3.
![]() -
биективным-
биекция(взаимно однозначные), если оно
одновременно инъективно и сюрьективно.
-
биективным-
биекция(взаимно однозначные), если оно
одновременно инъективно и сюрьективно.
![]() b
b![]() B
B
![]() a
a
![]() A : b=
f(a). ур.
имеет
ед.
решение.
A : b=
f(a). ур.
имеет
ед.
решение.
Например:
[-1,1]![]() [-1,1]
[-1,1]
f(x)=x2
[0,1]
 [-1,1]
[-1,1][-1,1]
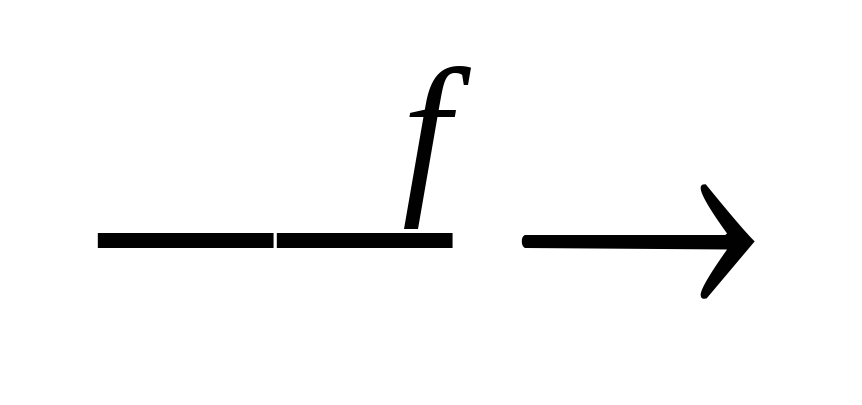 [0,1]
[0,1][0,1]
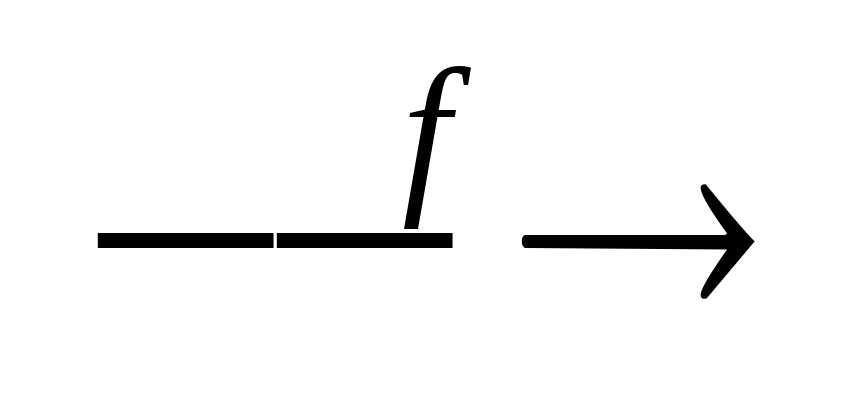 [0,1]
[0,1]
Некоторые свойства функций:
f(x)- называется четной, если
![]() x
x
![]() A => f(-x)=f(x).
A => f(-x)=f(x).
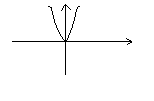
f(x)- нечетная, если
![]() x
x
![]() A
=> f(-x)=-f(x).
A
=> f(-x)=-f(x).
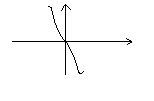
f(x)-
периодическая, если
![]() М >0, то
М >0, то
![]() x
x
![]() A
=> f(x+M)=f(x).
A
=> f(x+M)=f(x).
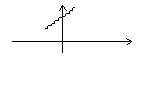
f(x)- возрастает, если x1 < x 2 => f (x1)< f (x2).
f(x)- убывает , если x1 > x 2 => f (x1)> f (x2).
Графики прямой и обратной функции, симметричной относительно прямой
x=y.

f(x)-
неубывающая, если x1
< x
2 => f
(x1)
![]() f
(x2).
f
(x2).
f(x)-
невозрастающая, если x1
> x
2 => f
(x1)
![]() f
(x2).
f
(x2).
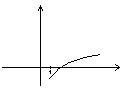
Если ф-ия равна постоянно, то она не убывает.
f(x) -ограничена сверху на E1, если
![]()
f(x) - ограниченна снизу на E1 ,если
![]()
Определение. f(x) –ограничена, если она ограничена сверху и снизу.
Утверждение: f(x)
-ограничена![]()
![]() k>0:
|f(x)|
k>0:
|f(x)|![]() k.
k.
Доказательство:
1). =>
![]() Е m
M
: m
Е m
M
: m![]()

2). <=
![]() k:
k:![]()
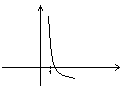
Основные элементарные функции
Степенная

ООФ:
![]() мн. знач.
мн. знач.![]()
(α>1) (α=1)


(0<α<1) (α=0)
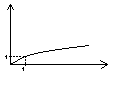

Показательные

(α>1) (0<α<1)


Логарифмическая

x>0 (a>0; a≠1)
(a>1) (0<a<1)
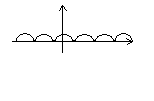
Тригонометрические
![]()

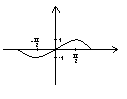
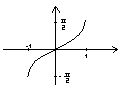
![]()
![]()


![]()
![]()
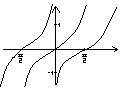

Элементарные функции- функции полученные из элементарными действиями (сложение, умножение и т.д.).
![]()
Рациональные функции
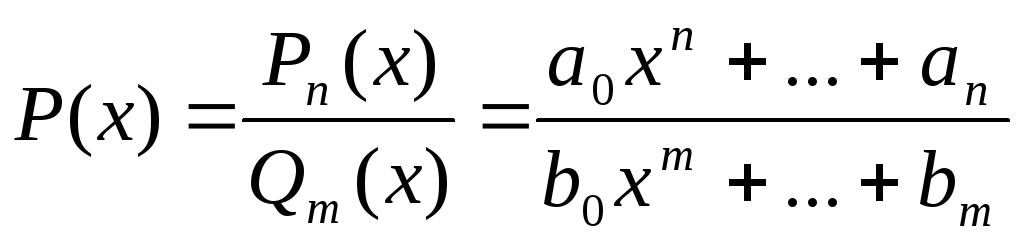
Неправильную рациональную дробь всегда можно представить в виде суммы правильного многочлена и правильной дроби.
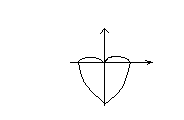
Полярная система координат
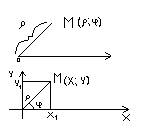
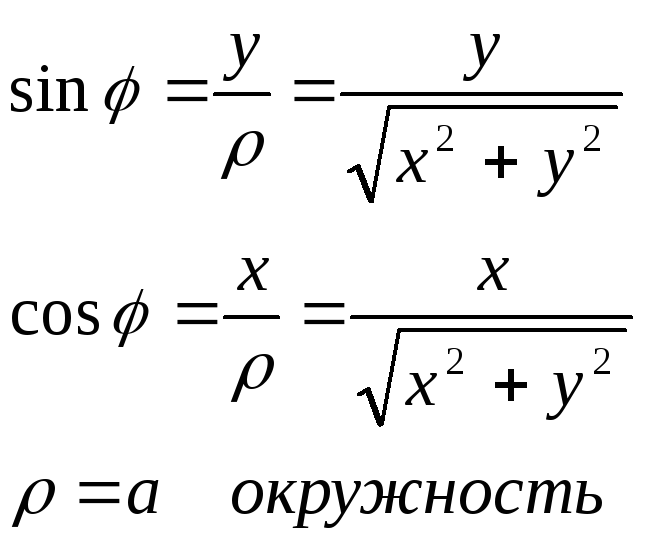

![]()

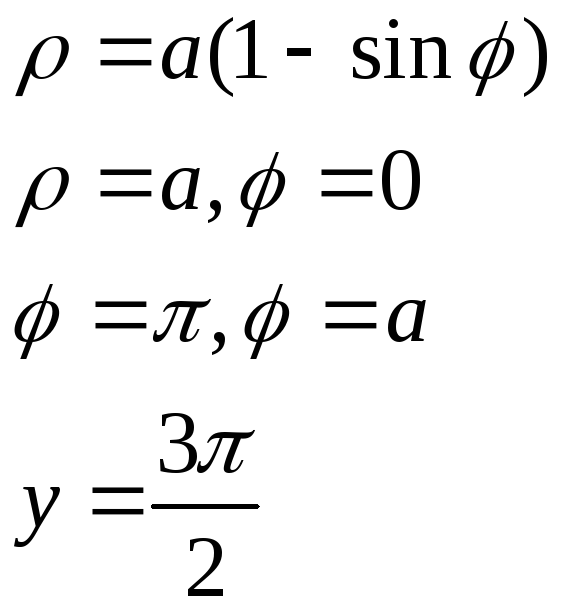
Параметрически заданная кривая
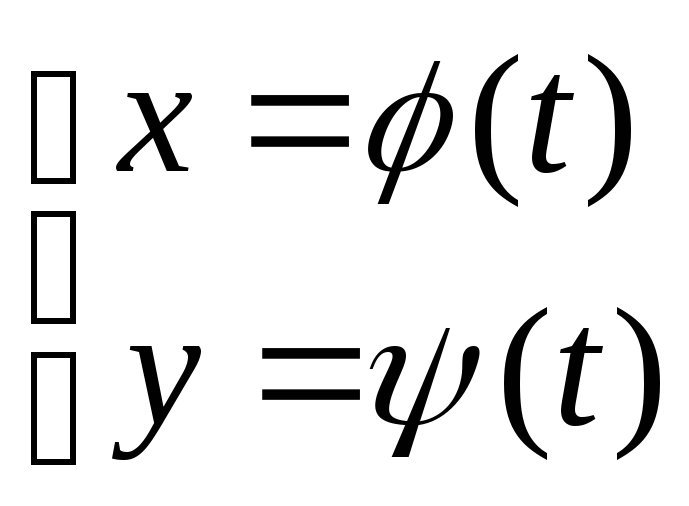
![]()





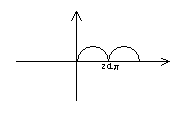
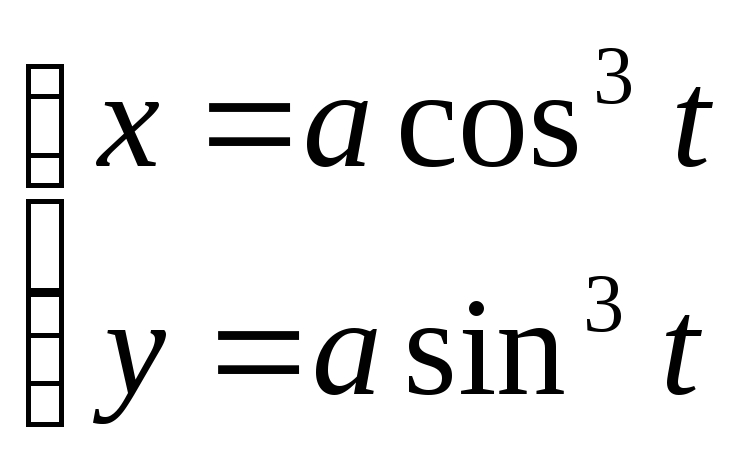
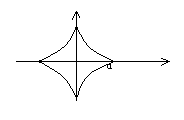
Пределы
Предел последовательности
![]() ф-ция определена наR
ф-ция определена наR
![]() - последовательность
- последовательность
Число а называют пределом
последовательностиаn
, если для любого положительного![]() найдется
такой номерn, начиная
с которого все члены последовательности
принадлежат последовательности
точки а
:
найдется
такой номерn, начиная
с которого все члены последовательности
принадлежат последовательности
точки а
:
![]()
![]()

наибольшее целое, не превосходящее а
Свойства предела.
Т![]() еорема
1. Предел
постоянной = самой постоянной.
еорема
1. Предел
постоянной = самой постоянной.
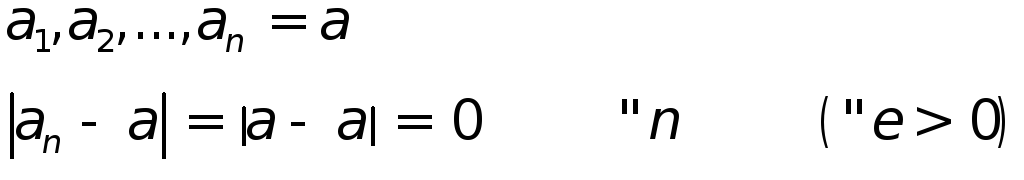 Д
– во:
Д
– во:
Теорема 2. Пост-ть не может иметь двух различных пределов, если предел
существует, то он единственный.
Д – во: (от противного)

пусть
противоречие : одно и то же число не может попасть в 2 не пересекающие
плоскости
Предел функции.
Н.р.
Окрестность бесконечности – это множество всех х
![]() удовлетворяющих
неравенству
удовлетворяющих
неравенству
![]()
Теорема об ограниченности
Е![]() сли
ф-ция имеет конечный предел, то она
ограничена в окрестности точки а.
сли
ф-ция имеет конечный предел, то она
ограничена в окрестности точки а.
огранич. в
Д – во:
ограничена
Односторонние пределы
 (предел
слева)
(предел
слева)
(предел справа)
Теоремы об односторонних пределах
Т
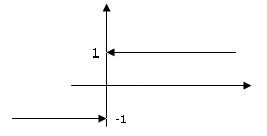 1.
Если сущ. односторонний предел, то сущ.
и односторонние пределы.
1.
Если сущ. односторонний предел, то сущ.
и односторонние пределы.
Т2. Если сущ-ют односторонние пределы, равные между собой, то сущ
обычный предел.
![]()
Бесконечно малые ф-ции

бесконечно большой, если ее предел
С в-ва
б/м
в-ва
б/м
Т1.
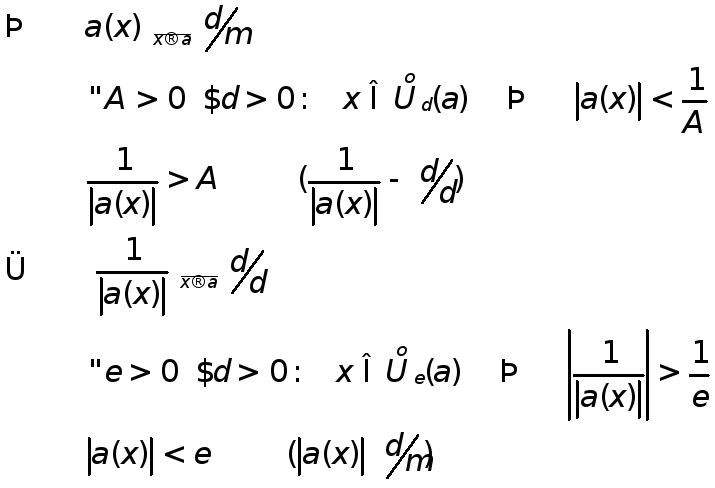
Д-во:
Т 2.
Сумма б/м есть б/м
2.
Сумма б/м есть б/м
Д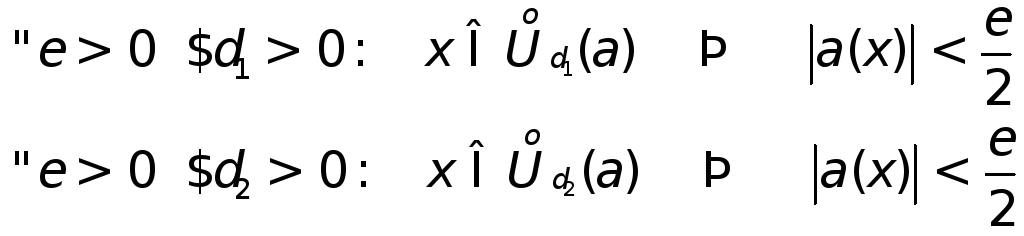 -во:
-во:
![]()
п![]() усть
усть
т.е.
Т![]() 3.
Произведение б/м ф-ций на ограниченную,
есть б/м
3.
Произведение б/м ф-ций на ограниченную,
есть б/м

![]()
ограничена в
![]()
Д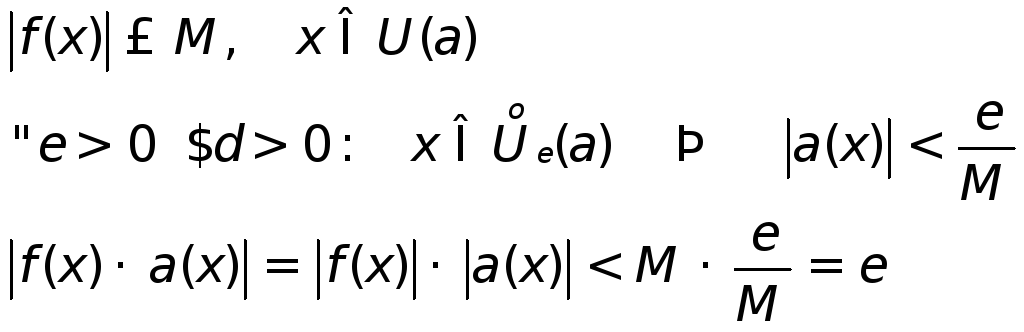 -во:
-во:
С![]() ледствия:
ледствия:
1. произведение б/м на const - б/м:
2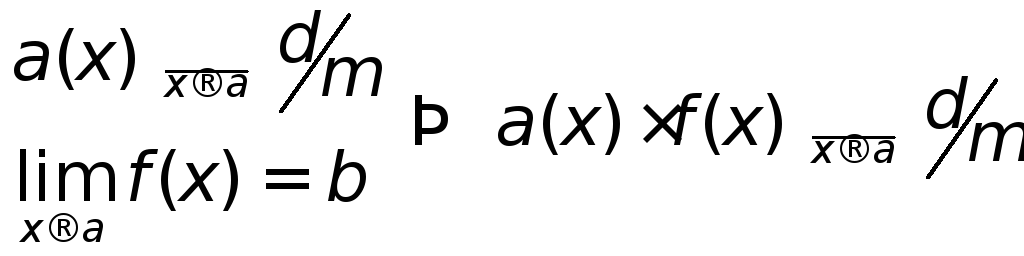 .
произведение б/м на ф-цию, имеющую
предел, - б/м
.
произведение б/м на ф-цию, имеющую
предел, - б/м
![]()
3. произведение 2-х б/м – б/м:
Т![]() еорема
1. критерий
существования предела
еорема
1. критерий
существования предела
Д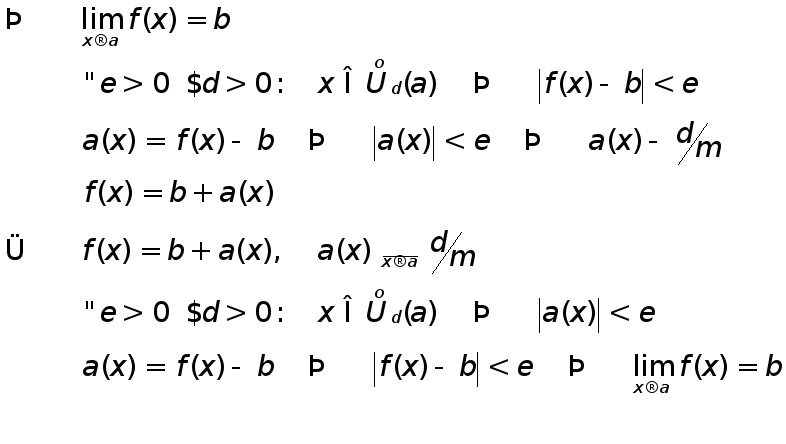 -во:
-во:
С войства
пределов:
войства
пределов:
Д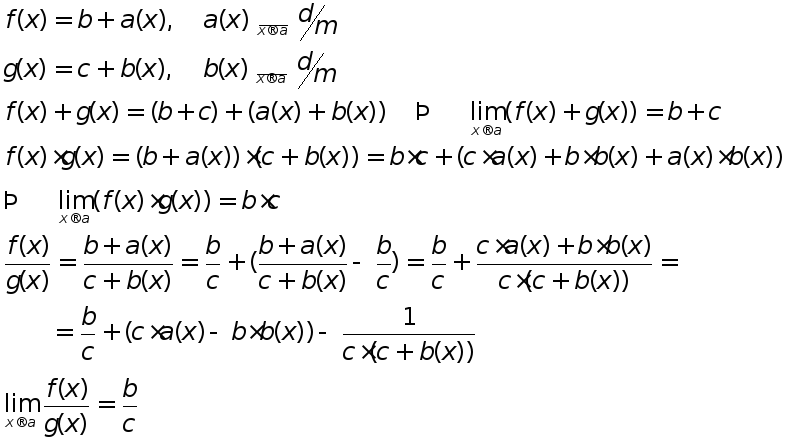 -во:
-во:
п![]() окажем,
что ограничена:
окажем,
что ограничена:

Теорема 2. о переходе к пределу в неравенстве
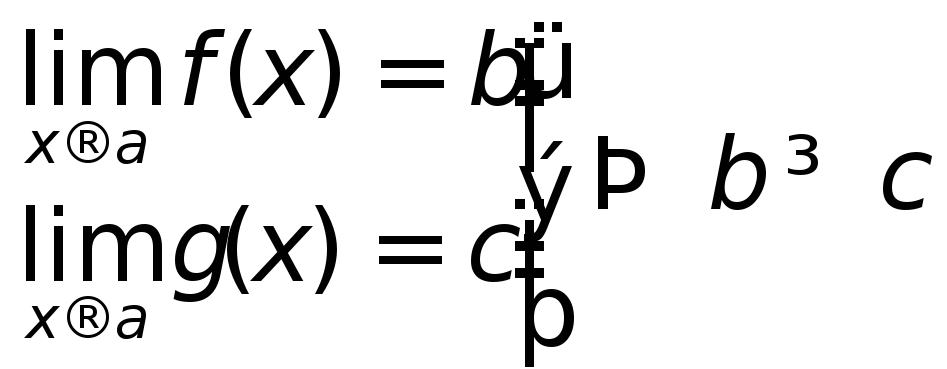
Д-во: (от противного)
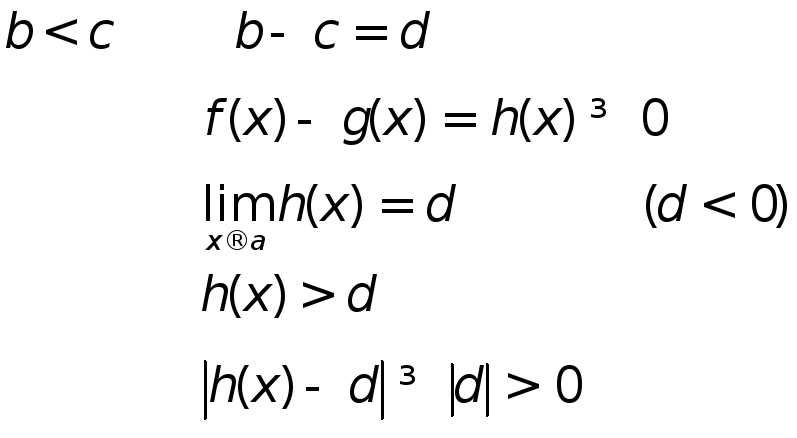
d не может быть пределом h(x)
Т еорема
3. (о двух
милиционерах)
еорема
3. (о двух
милиционерах)
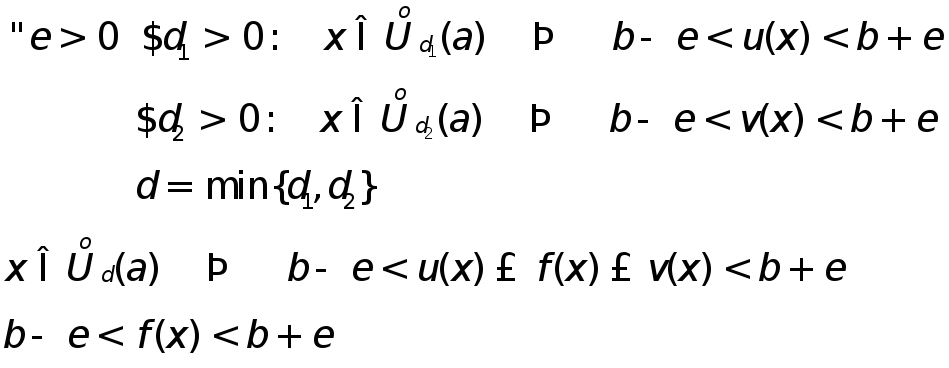
Д-во:
При переходе к пределу линейная операция сохраняется.
![]()
Некоторые свойства предела последовательности
1. если посл-ть имеет предел – она ограничена
![]() ограничена
ограничена
2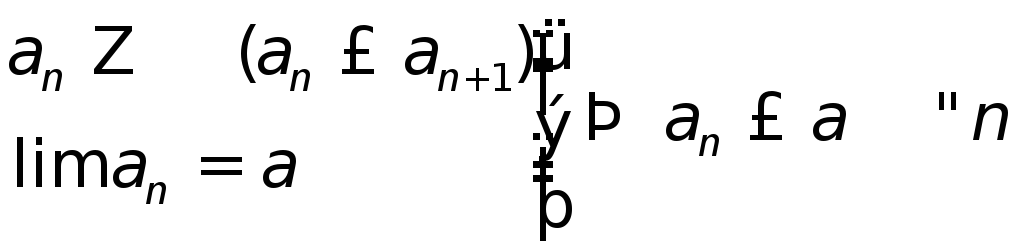 .
если посл-ть возрастает и имеет предел,
то она ограничена сверху своим
.
если посл-ть возрастает и имеет предел,
то она ограничена сверху своим
пределом:
3 .
если посл-ть возрастает и ограничена
сверху, то она имеет предел
.
если посл-ть возрастает и ограничена
сверху, то она имеет предел
Понятие непрерывности ф-ции
опр 1 : f(x)непрерывна иа, если![]()
![]()
опр 2: f(x)непрерывна иа, если![]()
Покажем, что это одно и то же:
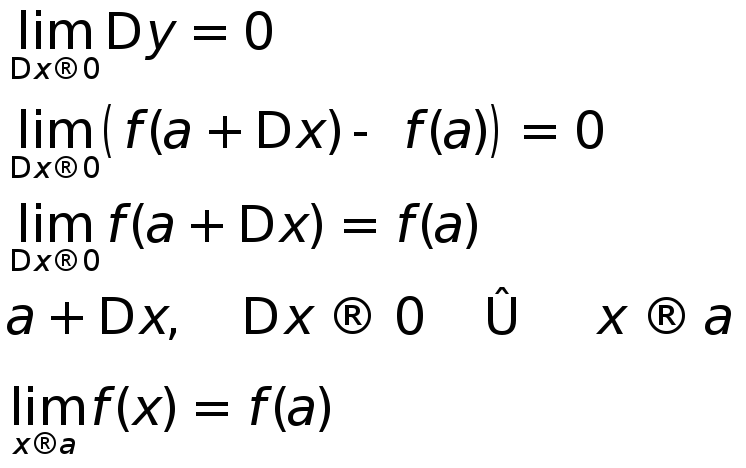
![]() непрерывность означает что предел
можно ввести под знак ф-ции.
непрерывность означает что предел
можно ввести под знак ф-ции.
С войства
непрерывности функции:
войства
непрерывности функции:
1. f(x)непрерывна ва
непрерывны в а
g(x)непрерывна ва
Если ф-ции непрерывны, то их линейные комбинации тоже непрерывны
2. Все элементарные функции непрерывны в каждой точке области их определения
3. f(x)непрерывна ва, g(x)непрерывна ва
![]() непрерывна ва
непрерывна ва
4. y=f(x) непрерывна ва
![]() обратная функция
обратная функция![]() непрерывна вb=f(a)
непрерывна вb=f(a)
![]() следует из непрерывности функции
следует из непрерывности функции
I замечательный предел
Теорема.![]()


![]() справедливо и для x<0,
т.к. еслиx заменить
на - x, то ничего
не
справедливо и для x<0,
т.к. еслиx заменить
на - x, то ничего
не
изменится – все функции четные
![]()
![]()
![]()
II замечательный предел
Теорема(вспомогательная) последовательность
![]() ,
где
,
где![]() имеет предел
имеет предел![]() ,
заключенный на отрезке
,
заключенный на отрезке![]()
Д-во:
![]()
![]() число сочетаний поk-элементов
из n
число сочетаний поk-элементов
из n
![]()
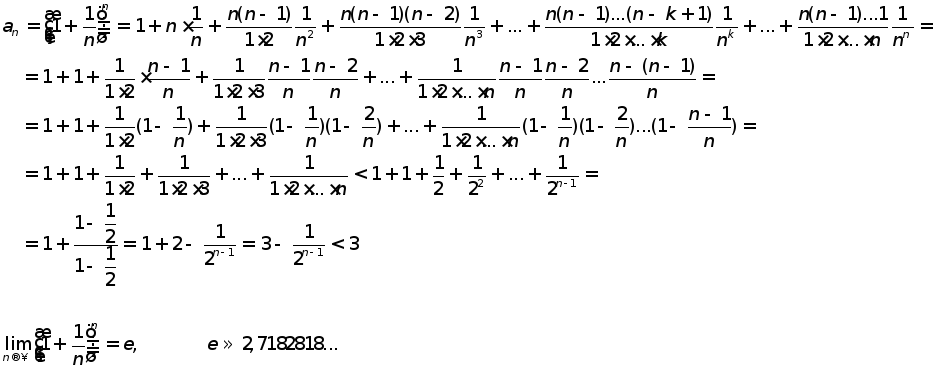
Теорема Второй замечательный предел
![]()
Д-во:
х>0:![]()

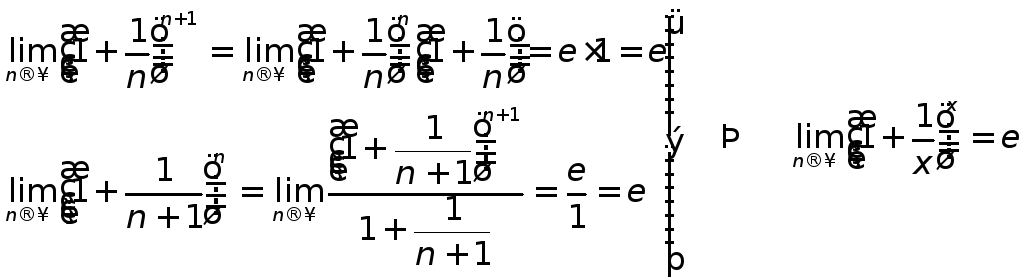
х<0: обозначим t=-(x+1)

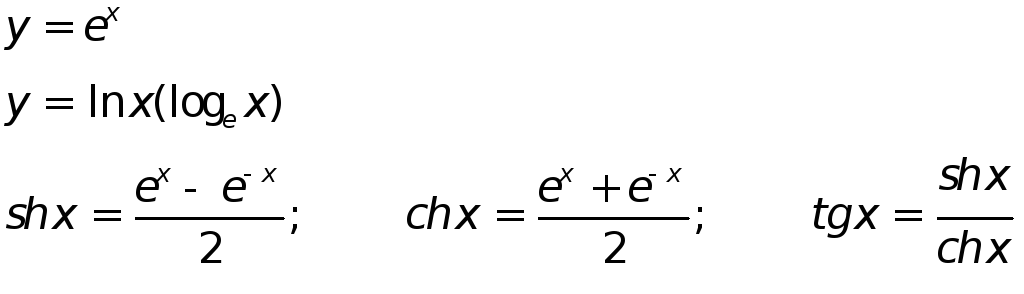
Следствия II замечательного предела:
1.
![]()
Д-во:
![]()
![]()
2.
![]()
ln– это не предельная функция, поэтому знак предела можно вынести под знакln
3.
![]()
Д-во:

Сравнение бесконечно малых
![]()
Опр. 1
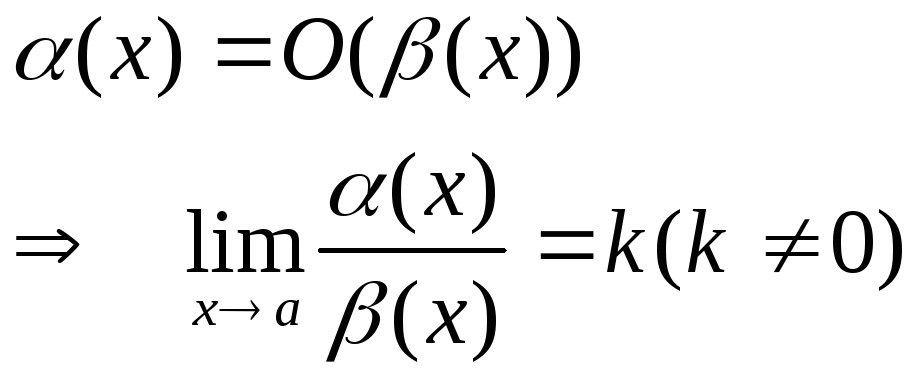
Опр. 2
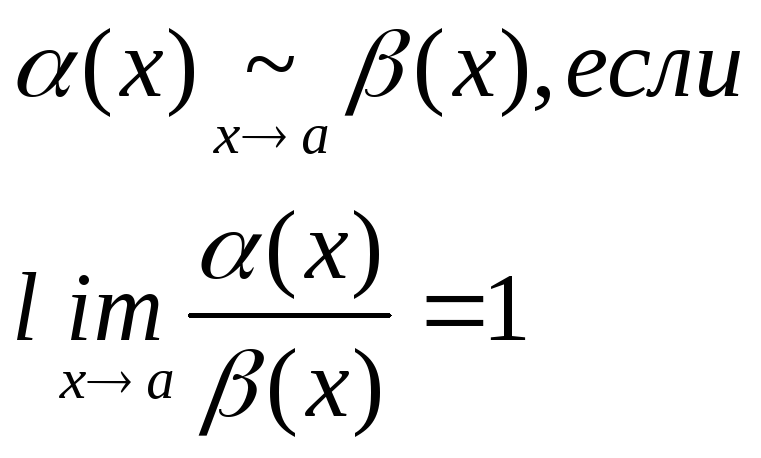
Опр. 3
![]()
Опр. 4
![]()
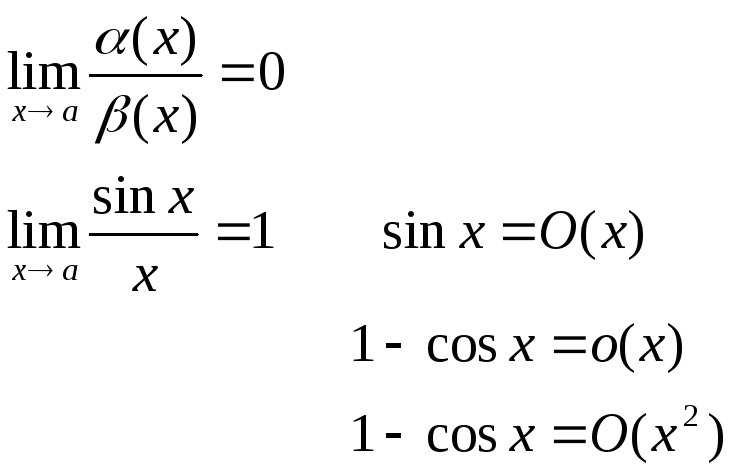
Таблица эквиволетности б/м
Т-1.
![]()

Точки разрыва функций
y=f(x) x=a- точка разрыва функции f(x), если коор. условия непрерывны.
x=a-
т. непрер.
оси ![]()

2) 
![]()

3. ![]()
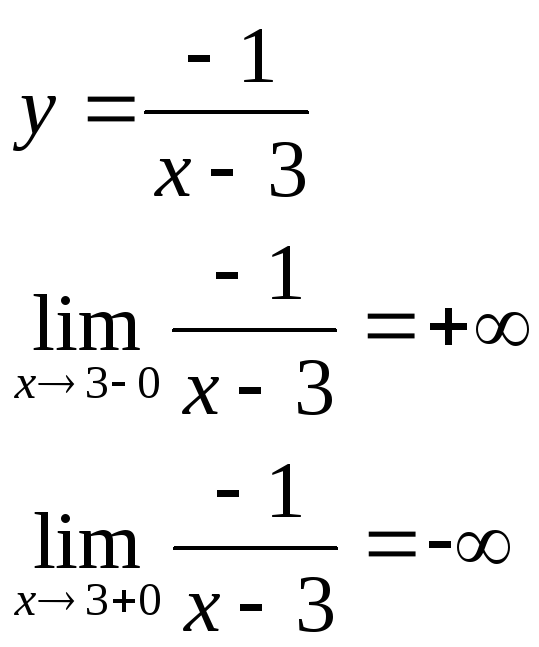
Однородная непрерывность
y=f(x) – непрерывна слева(справа)
если :
![]()
y=f(x) – непрерывна на интервале (a,b), если f(x) непрерывна
y=f(x) – непрерывна на отрезке [a,b] если непрерывна на интервале (a,b)
f(x) непрерывна слева в (.) b
f(x) непрерывна справа в (.) а
Свойства функций не прерывных на замкнутом отрезке
1. f(x) непрерывна на [a,b]


2.
f(x) непрерывна на [a,b]
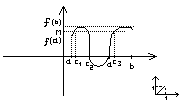
3. f(x) непрерывна на [a,b]

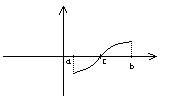
Производная функции.
Y=f(x) определилась в окрестности U(Xo)
![]()
![]() - функция, которая
имеет производную, называется
дифференцируемой.
- функция, которая
имеет производную, называется
дифференцируемой.
Теорема: (о непрерывности дифференцируемой функции)
Если функция дифференцируема в Хо, тогда она непрерывна в этой точке.
Док-во:
![]() ,
тогда
,
тогда
![]()
![]()
![]()
![]()
Значение f(x) непрерывно
Y(x)
Xо=0,
![]() функция непрерывна.
функция непрерывна.
Если
![]() ,
,
![]()
 нет предела.
нет предела.
Функция не дифференцируема
Основные формулы дифференцирования.
1. (С)`=0
Док-во:
![]()
![]()
![]()
2.
![]() (сложение)
(сложение)
Док-во:
![]()
![]()
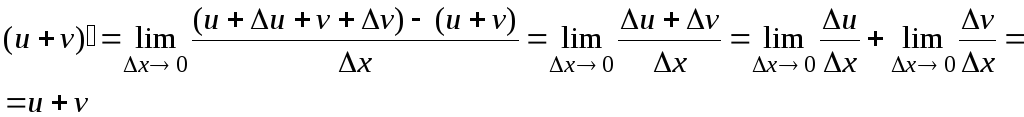
3.
![]()
Док-во:
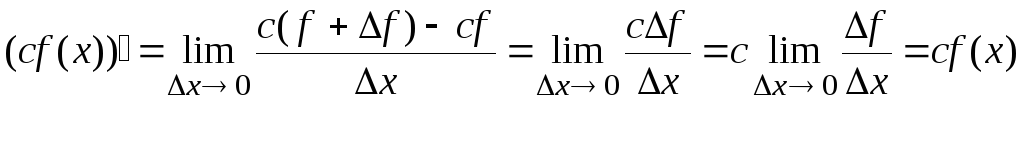
Производная сохраняет линейные комбинации.
4. Производная произведения:

5. Производная частного:
![]()
Док-во:
![]()
![]()
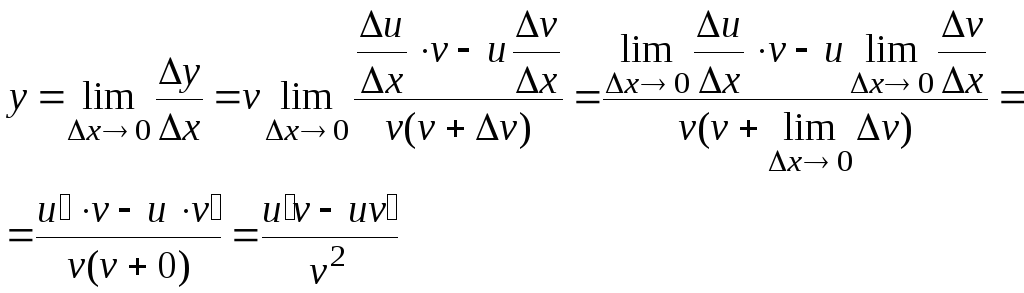
6.Производная сложной функции:
![]()
Док-во:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
7. Производная обратной функции
![]()
![]()
Док-во:
![]()
Если
![]()
Если
![]()
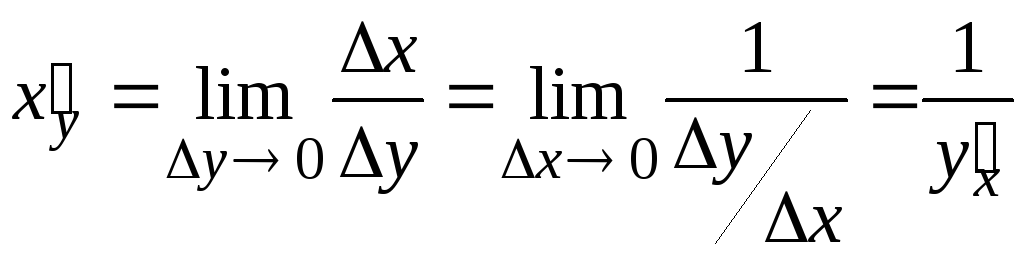
8. Производная параметрически заданной функции:

Док-во:

![]()
![]()
Производные элементарных функций
1.
![]() ,
,![]()
![]()
![]()
2.
![]()
![]()
![]()
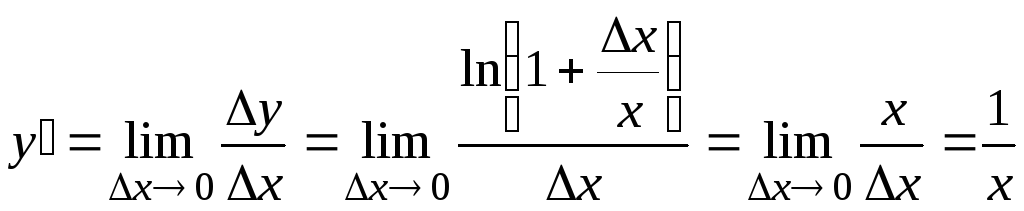
3.
![]()
![]()
![]()
![]()
4.
![]() ,
,![]() ,
,![]()
![]()
5.
![]()
![]()
6.
![]() ,
,![]()
![]()
![]()
![]()
7.
![]()
![]()
8.
![]()
![]()
9.
![]()
![]()
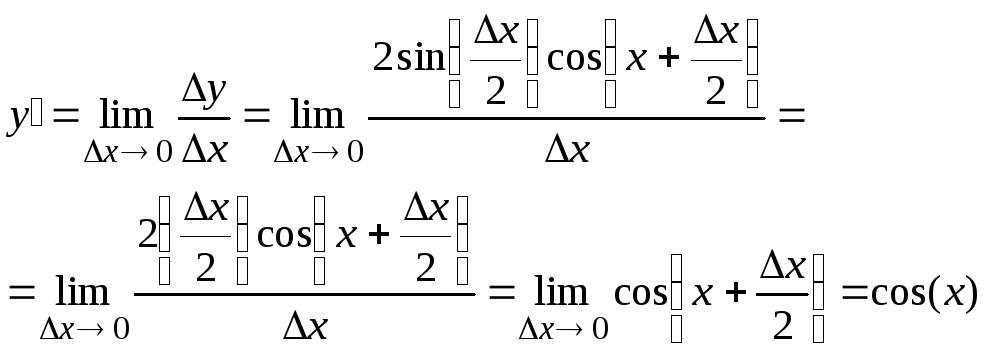
10.
![]()
![]()
![]()
11.
![]()
![]()
![]()
12.
![]()
![]()
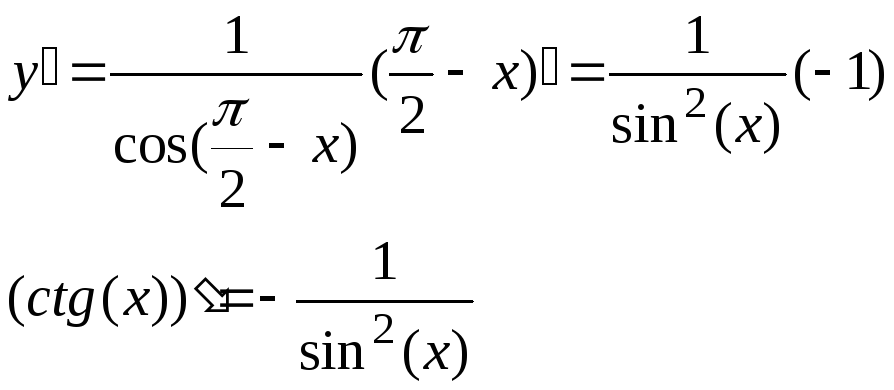
13.
![]() ,
,![]()
![]()
14.
![]() ,
,![]()
![]()
15.
![]() ,
,![]()
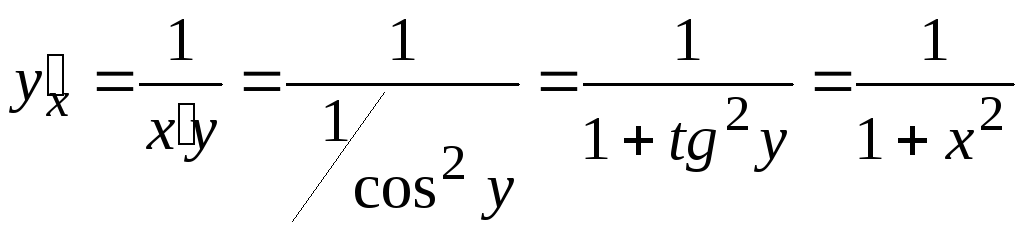
16.
![]() ,
,![]()
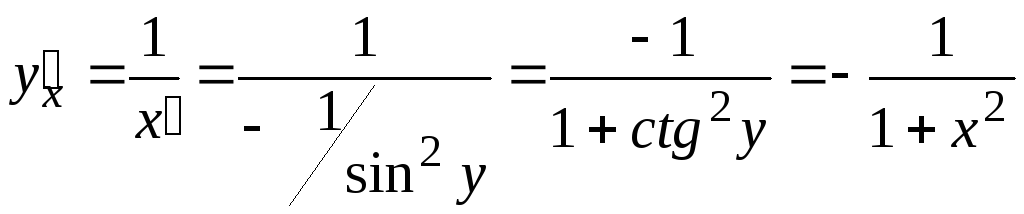
Примеры:
1.
![]()
2.

![]()
3.
![]()
![]()
![]()
![]()
![]()
4.
![]()
![]()
![]()
![]()
Механический смысл производной
Геометрический смысл производной.
![]() (фиксированная
точка)
(фиксированная
точка)
![]() (текущая)
(текущая)
Касательная
![]()
![]() (предельное
положение секущей)
(предельное
положение секущей)
![]()
![]() то
то
![]()
![]()
![]()
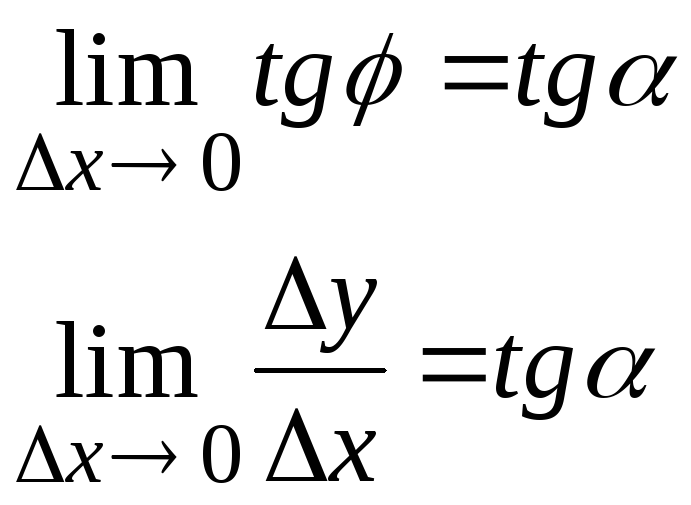
![]()
![]()
![]()
![]() - уравнение
касательной
- уравнение
касательной
![]() - уравнение прямой
- уравнение прямой
![]() - нормали
- нормали
Дифференцируемость функции. Дифференциал.
![]() определена
в
определена
в![]()
![]()
Опр.![]()
Т.
![]() диф.
в
диф.
в![]()
Д.
![]()
![]() в
в![]()
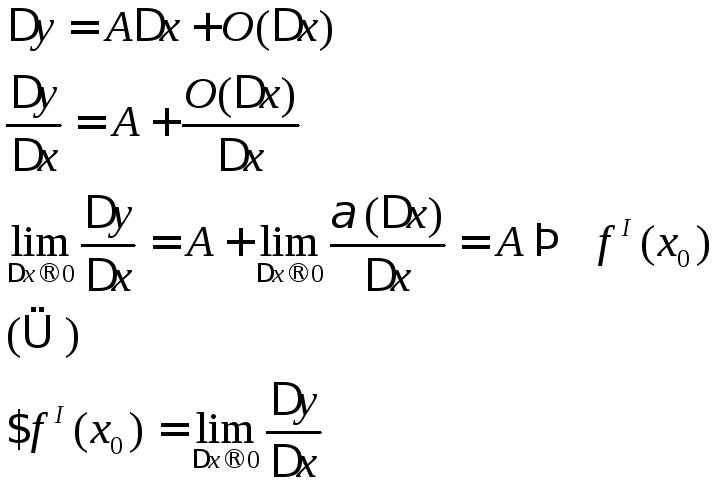
![]()
![]() -
б/м
-
б/м
![]()
![]() =A
=A
![]() =
=![]()
Опр.![]()
![]()
Диф. лин. часть примера
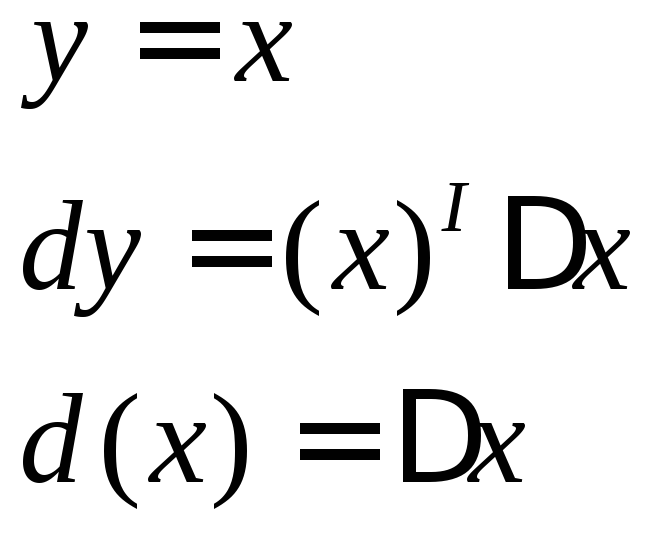
![]()
Геометрический смысл диап.
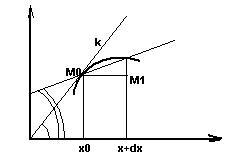
![]() -
уравнение касательной
-
уравнение касательной
![]()
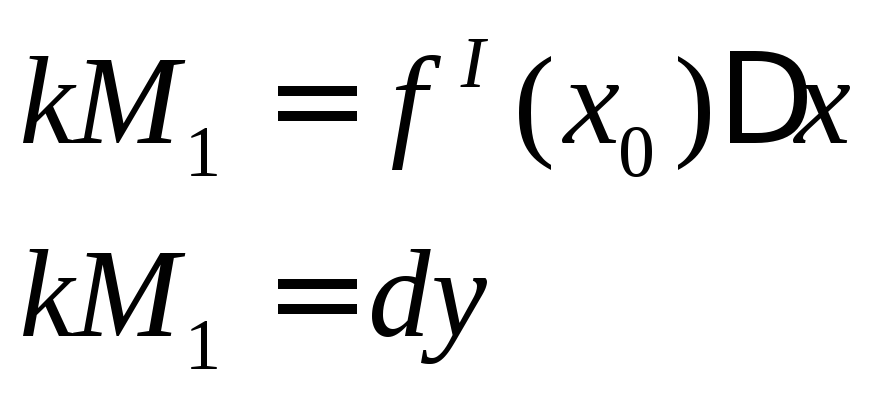
Применение диф. прибл. к функции
![]()
![]()
![]()
![]()
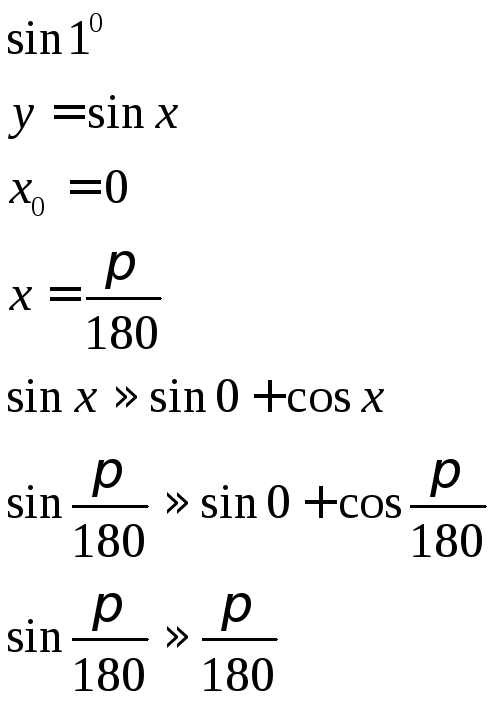
Свойства дифференциалов:
1)
![]()
2)
![]()
3)
![]()
4)
![]()
5)
![]()
6)Форма дифференциала инвариантна (неизменна)
![]()
![]()
Д.
![]()
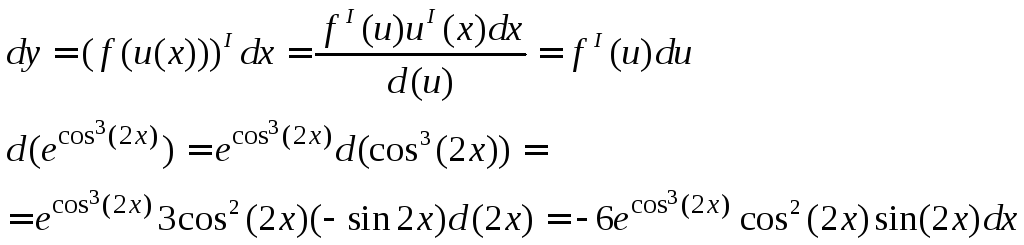
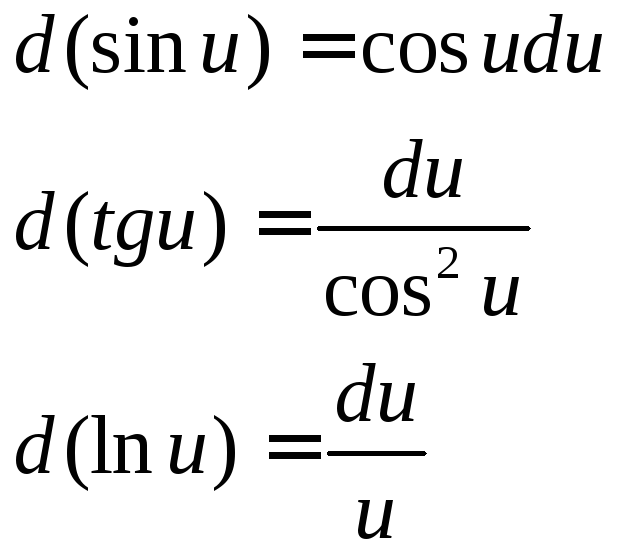
Производные и дифференциалы высших порядков.

![]()
![]()


![]()
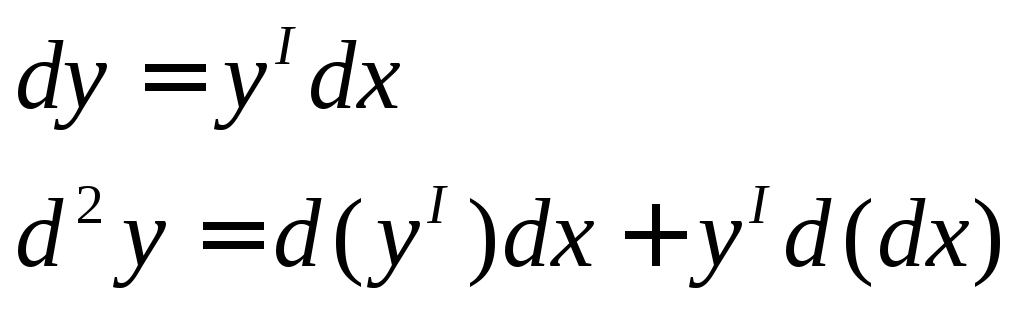
1)x– нед. пер.![]()
![]() ,
еслиx– недов. перем.
,
еслиx– недов. перем.
2)
![]()
![]()
![]() - формула
- формула
Производная первой функции
![]()
![]()
![]()


Основные теоремы дифференциального исчисления
Т. Ферма
Пусть ф.
![]() непрерывна на
непрерывна на![]() ,
диф. на
,
диф. на![]() достигает
своего наибольшего и наименьшего
значения:
достигает
своего наибольшего и наименьшего
значения:
![]()
![]()
Д.
![]()
![]()
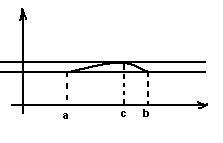
Т. Ролля.
![]()
![]() непрерывна на
непрерывна на![]() ,
диф. на
,
диф. на![]()
![]()
Д.
Наибольшее
![]() ,
наименьшее
,
наименьшее![]() .
.
![]()
1)
![]()
![]()
2)
![]()
![]()
![]()
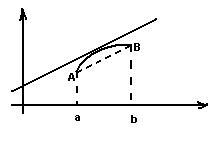
Т. Логранжа.
![]() непрерывна на
непрерывна на![]() ,
диф. на
,
диф. на![]()
![]()
Д.
![]()
![]() непрерывна на
непрерывна на![]() ,
диф. на
,
диф. на![]()
![]()
![]()
![]()
![]()
![]()
![]() -
угловой коэф. конст.
-
угловой коэф. конст.
![]()
![]() ,
,![]()
![]() =k
=k
![]()
Т. Коши.
![]() непрерывна на
непрерывна на![]() ,
диф. на
,
диф. на![]()
![]()
![]()
![]()
Д.
![]()
![]() непрерывна на
непрерывна на![]() ,
диф. на
,
диф. на![]()
![]()

Теорема Логранжа – частный случай теоремы Коши
Т. Лопиталя ![]()
![]() удовлетворяют условиям т. Коши
удовлетворяют условиям т. Коши

Д.
![]()
![]()
![]()
![]()
Замечание.
Вместо
![]() можно
можно![]()
Дифференциальные уравнения
![]()
![]()
![]()
Уравнения первого порядка
![]() (1)
(1)
![]()
![]()
![]() (2)
(2)
Задача Каши
Это поиск решения
уравнения
![]() с начальными условиями (2).
с начальными условиями (2).
Теорема (о существовании решения задачи Каши)
![]() - непрерывная и
дифференцируемая функция в области
- непрерывная и
дифференцируемая функция в области
![]()
![]() - ограничена
- ограничена
![]()
![]() !
Решение уравнения
!
Решение уравнения![]() ,
удовлетворяющего условию (2)
,
удовлетворяющего условию (2)
Интегральная кривая – решение дифференциального уравнения
Решая уравнение
![]() будем получать семейство кривых
будем получать семейство кривых
![]() - общее решение
(
- общее решение
(![]() )
)
1)
![]() удовлетворяет (
удовлетворяет (![]() )
при
)
при![]() с
с
2) при
![]() (2)
(2)![]() !
!![]() при котором
при котором![]() удовл. (
удовл. (![]() )
и (2)
)
и (2)
![]() - частное решение,
удовл. (2)
- частное решение,
удовл. (2)
Уравнения с разделяющимися переменными.
![]() |
|![]()
![]()
![]()
![]()
![]() ,
, ![]()
![]()
iПример.
![]()
![]()
![]()
![]()
![]()
Задача о распаде радиоактивного вещества.
Скорость распада радиоактивного вещества пропорционально массе вещества. Найти закон распада и период полураспада.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Т – период полураспада
![]()
![]()
![]()
Уравнение с однородными множителями
![]() (*)
(*)
M, N – однородные функции одной степени
![]() - однородная функция
степени
- однородная функция
степени![]() ,
если
,
если![]()
![]()
Решение.
Уравнение сводится
к виду
![]() (**)
(**)
![]()
![]()
![]()
![]()
![]()
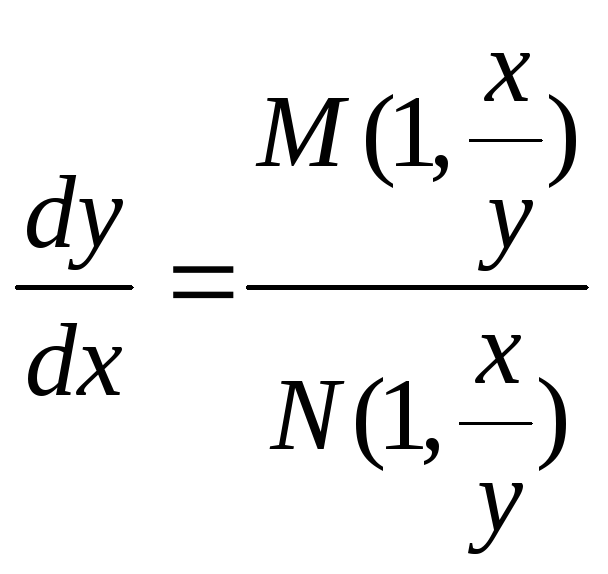
![]()
![]() (уравнение
с разделяющимися переменными)
(уравнение
с разделяющимися переменными)
Пример.
![]()
![]()
![]()
![]()
![]()
![]()
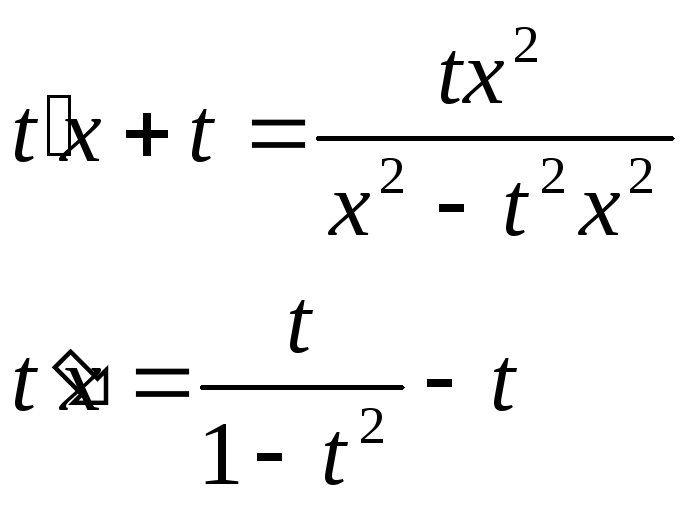
![]()
![]()
![]()
![]()
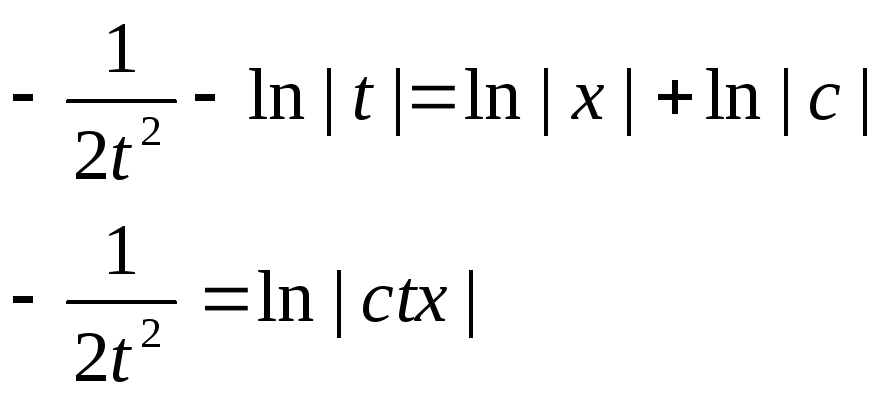
![]()
![]()
Линейные уравнения
![]()
![]() (1)
(1)
![]()
![]() (2)
(2)
1способ
![]()
![]()
![]()
![]()


2способ
Решаем (2)
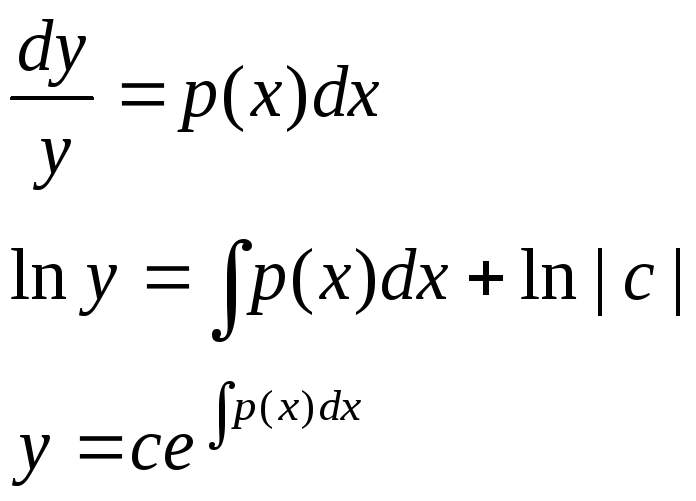
Подставим
в (1)и найдём
![]() .
.
Лекция №11
Применение дифференциального исчисления к исследованию функций.
1.Монотонность
Теорема 1(необходимое условие монотонности)
![]() - непрерывна и дифференцируема
- непрерывна и дифференцируема

Доказательство

Теорема 2 (достаточное условие монотонности)
![]() - непрерывна и дифференцируема
- непрерывна и дифференцируема

Доказательство
![]()
![]()
 (две
произвольные точки)
(две
произвольные точки)


![]() C
C
![]()
![]()
2. Экстремумы
Определение.
![]() определена в окрестности
определена в окрестности![]()
![]() - точка максимума функции, если
- точка максимума функции, если![]()
![]()
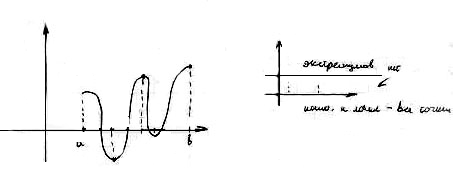
Теорема 1. (Необходимое условие экстремума)
![]() - непрерывна и дифференцируема в
- непрерывна и дифференцируема в![]()
![]() - точка экстремума функции
- точка экстремума функции
![]()
![]()
Доказательство.


![]()
![]()
![]()
![]() - точка минимума
- точка минимума![]()
![]()
![]()
![]()
![]()
![]() ;
;![]()
![]()
![]()
![]() ;
;![]()
![]()
![]()
![]() .
.
Стационарные точки – точки, в которых производная равна нулю.
Критические точки – точки, в которых производная равна нулю или имеет разрыв.
Экстремумы могут находится только среди критических точек.
Теорема 2.(достаточное условие экстремума)
![]() - непрерывна
- непрерывна![]() и
дифференцируема в
и
дифференцируема в![]()
![]() - критическая точка
- критическая точка
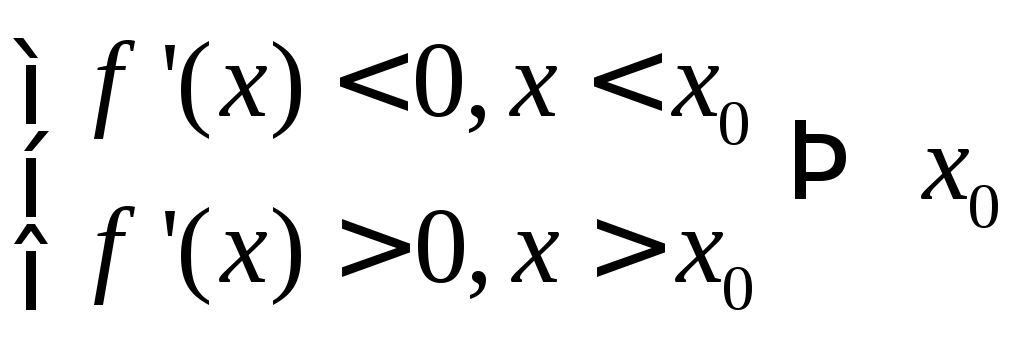 - точка минимума
- точка минимума
 - точка максимума
- точка максимума
Доказательство.
C




![]()
![]()
![]()
 - точка минимума
- точка минимума
Теорема 3.(Исследование на экстремум с помощью второй производной)
![]() - непрерывна в
- непрерывна в![]()
![]() - непрерывна в
- непрерывна в![]()
![]()
![]()
![]() - точка максимума
- точка максимума
![]() - точка минимума
- точка минимума
Доказательство.
![]()
![]()
![]() ,
,![]()
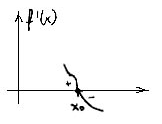
![]() -
точка максимума
-
точка максимума
3.Вогнутость.

Кривая называется вогнутой вверх (выпуклой) , если она лежит ниже касательной проведённой в любой точке отрезка.

Если кривая лежит выше касательной то она вогнута книзу или просто вогнута.
Теорема 1. (необходимое условие вогнутости)
![]() - непрерывна и дифференцируема
- непрерывна и дифференцируема
Если
![]() вогнута кверху
вогнута кверху![]()
![]()
Если
![]() вогнута книзу
вогнута книзу![]()
![]()
Д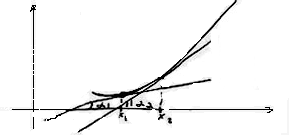 оказательство.
(нестрогое доказательство)
оказательство.
(нестрогое доказательство)
![]()
Если кривая вогнута книзу то первая производная возрастает.

Теорема 2. (достаточное условие вогнутости)
![]() - непрерывна и дифференцируема
- непрерывна и дифференцируема
Если
![]() ,
то
,
то
![]() вогнута книзу
вогнута книзу
Если
![]() ,то
,то
![]() вогнута кверху
вогнута кверху
Доказательство.
![]()
![]() -
кривая
-
кривая
![]() - касательная
- касательная
![]()
![]()
![]()
![]() справа и слева. Ч.Т.Д.
справа и слева. Ч.Т.Д.
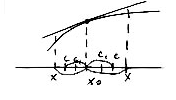
4.Перегибы.
![]() -точка
перегиба кривой
-точка
перегиба кривой
![]() если
с одной стороны она вогнута кверху, а с
другой вогнута книзу.
если
с одной стороны она вогнута кверху, а с
другой вогнута книзу.
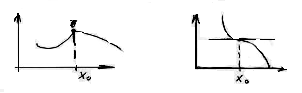
Теорема 1.(необходимое условие перегиба)
![]() - непрерывна и дифференцируема в
- непрерывна и дифференцируема в![]()
![]() -точка
перегиба
-точка
перегиба![]()
![]()
Доказательство.
Точка перегиба - точка экстремума для производной в критических точках второго порядка, нужно искать экстремумы.
Теорема 2.(достаточное условие перегиба)
![]() - непрерывна в
- непрерывна в![]()
![]() - непрерывна в
- непрерывна в![]()
![]() -
непрерывна в
-
непрерывна в![]()
![]() или
или![]()
Если производная второго порядка меняет
знак при переходе через точку
![]() ,
то
,
то![]() -точка
перегиба.
-точка
перегиба.
Доказательство.
Следует из основного условия для экстремума.
5.Асимптоты.
1) Вертикальные асимптоты
![]() называется
асимптотой
называется
асимптотой
![]() ,
если
,
если![]()

2) Наклонные асимптоты
![]() называется
наклонной асимптотой
называется
наклонной асимптотой
![]() ,
если
,
если![]()
![]() называется асимптотической кривой для
называется асимптотической кривой для
![]() ,
если
,
если![]()
Вывод уравнения наклонной асимптоты.
![]() (1)
(1)

![]() подставляем в формулу (1)
подставляем в формулу (1)
![]()
Формула Тэйлора
![]() имеет непрерывную производную до пар
имеет непрерывную производную до пар![]() в
в![]()

Пусть
![]() имеет непрерывную производную до порядка
имеет непрерывную производную до порядка![]() в
в![]()
![]()
![]() +
+![]()
![]()
![]() (Формула Макларена)
(Формула Макларена)
![]()
![]()
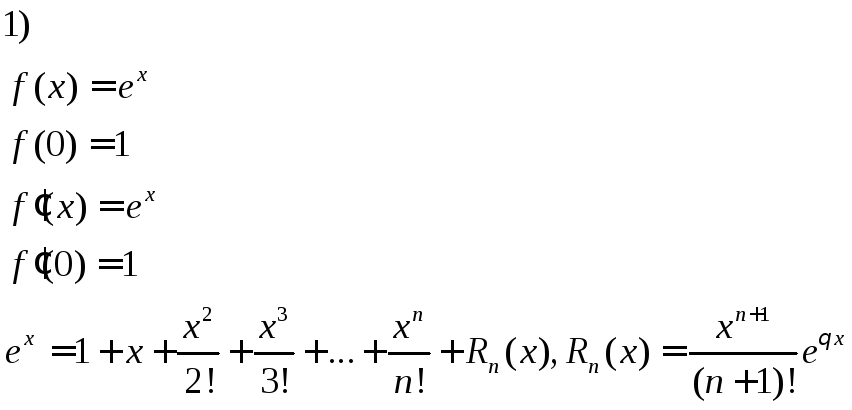
2)

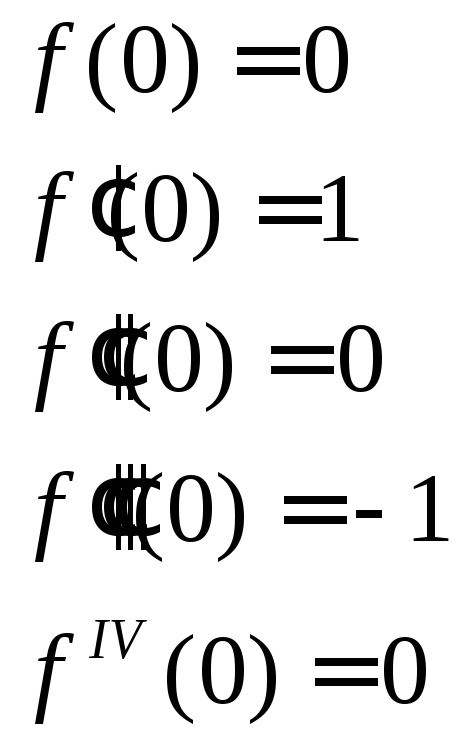
![]()
3)

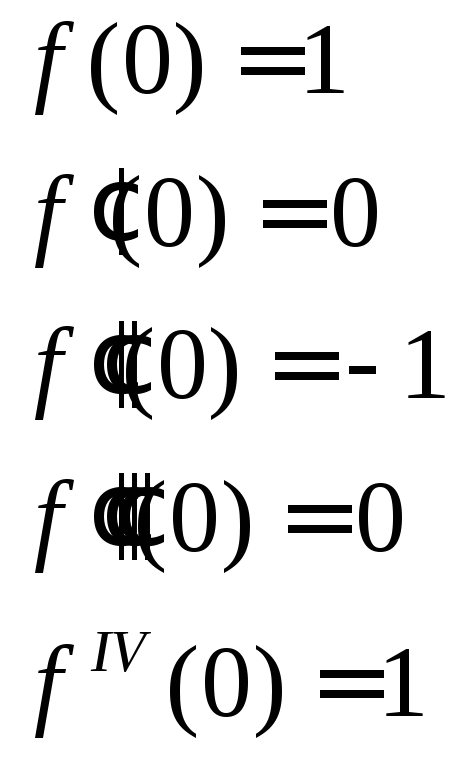
![]()
4)

5)
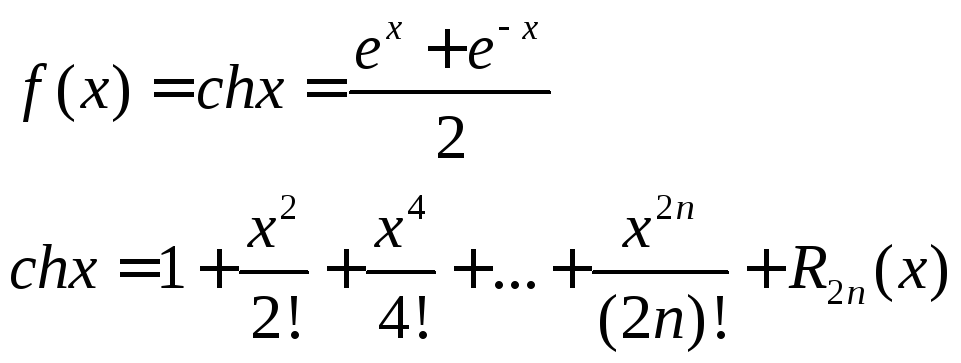
6)
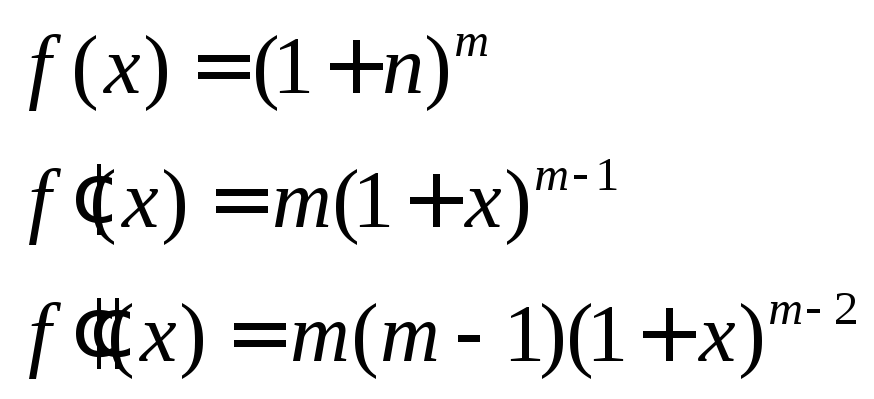

![]()
7)
![]()
8)
![]()
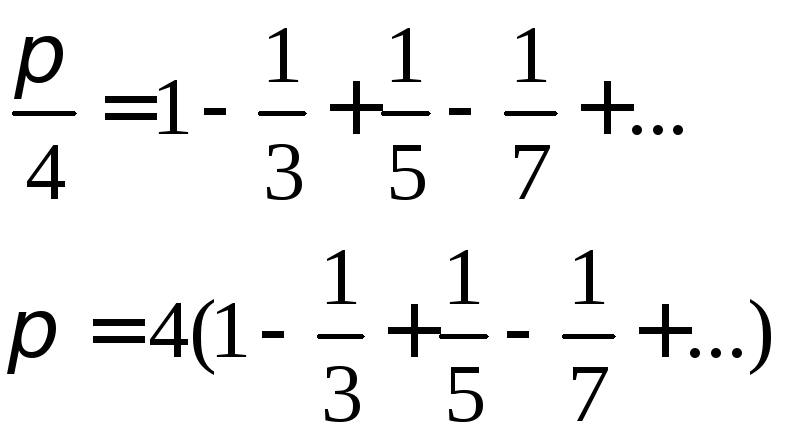
Исследование функций на экстремумы с помощью формулы Тэйлора.
Теорема 1.
Пусть
![]() имеет непрерывную производную до порядка
имеет непрерывную производную до порядка![]() в
в![]()
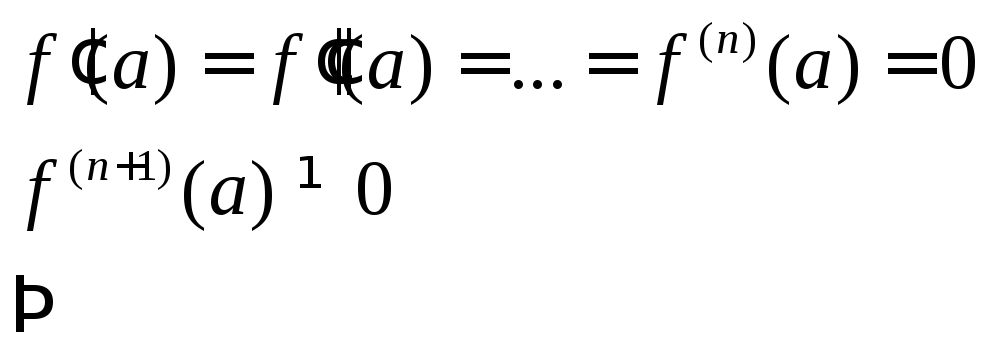
1)
![]() - четная
- четная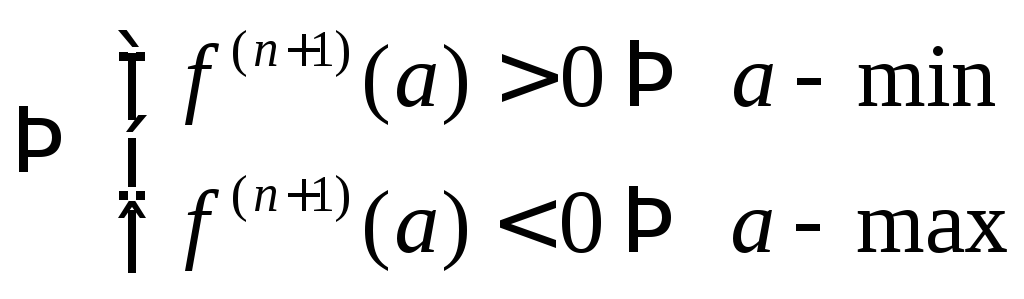
2)
![]() - нечетная
- нечетная![]() нет
экстремума в точке
нет
экстремума в точке![]()
(![]()
![]() - точка перегиба)
- точка перегиба)
Доказательство.
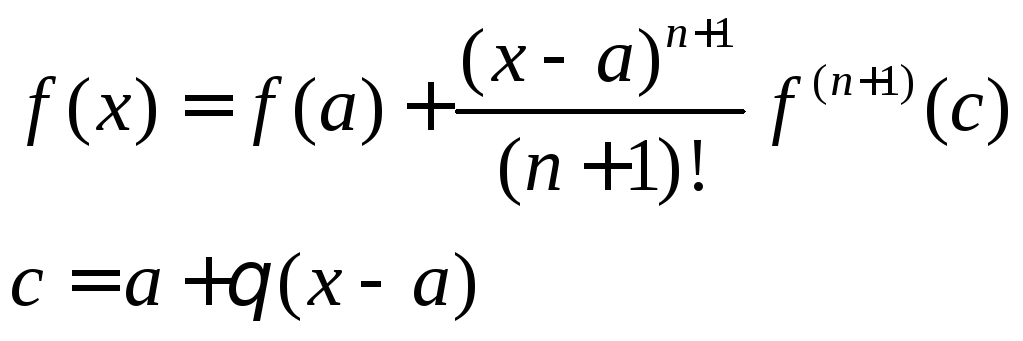

 aCx
aCx
1)
![]() - четная
- четная![]()
![]()
![]()
![]() поскольку произведение непрерывно то
знак совпадёт со знаком функции в точке
а.
поскольку произведение непрерывно то
знак совпадёт со знаком функции в точке
а.![]() - точка минимума
- точка минимума
![]() -
точка максимума
-
точка максимума
2)
![]() - нечетная
- нечетная![]()
![]() меняет знак
меняет знак
![]() не меняет знака
не меняет знака
![]() меняет знак
меняет знак![]() нет экстремума
нет экстремума
Функции нескольких переменных
Z=f(x,y)
Для любых x,y->z
Окрестностью точки на плоскости называется круг с центром в этой точке.
(x-xо)2+(y-yo)2<z2
Ur(Mo) –r– окрестностьMo
![]()
![]() r(Mo)
– проколотая окрестность
r(Mo)
– проколотая окрестность
Точка Moназывается внутренней точкой множестваD. ТочкаMназывается внутренней если она принадлежит
множеству вместе с некоторой своей
окрестностью.M1 –
граничная точкаDесли в
любой ее окрестности найдутся точки
принадлежащие и не принадлежащие.
Совокупность граничных точек называется
границей.![]() D– граница множестваD.M2- изолированная
точка множестваD, если в
некоторой ее окрестности нет других
точек множестваDкроме
ее самой. МножествоDназывается открытым если состоит только
из внутренних точек. множествоDназывается замкнутым если содержит все
граничные точки.
D– граница множестваD.M2- изолированная
точка множестваD, если в
некоторой ее окрестности нет других
точек множестваDкроме
ее самой. МножествоDназывается открытым если состоит только
из внутренних точек. множествоDназывается замкнутым если содержит все
граничные точки.
![]() - замыкание
- замыкание
Множество Dназывается связным если 2 любые точки множестваDможно соединить непрерывной кривой лежащей вD.
Область – открытое связное множество.
Множество называется ограниченным если его можно поместить внутри круга конечного радиуса, в противном случае оно неограниченное. Односвязное множество – если любую замкнутую прямую, лежащую в Dможно непрерывной деформацией стянуть в точку не покидая множестваD.
Непрерывность функции
Функция z=f(x,y) называется непрерывной
в точке (xo,yo)
если![]() f(x,y)
=f(xo,yo)
или
f(x,y)
=f(xo,yo)
или![]()
![]() f=0.
f=0.
Частные приращения
Дадим приращение аргументу x=xo+![]() x
x![]()
![]() xf=f(xo+
xf=f(xo+![]() x,yo) -f(xo,yo)
x,yo) -f(xo,yo)
y=yo+![]() y
y![]()
![]() yf=f(xo,yo+
yf=f(xo,yo+![]() y)
-f(xo,yo)-
полное приращение
y)
-f(xo,yo)-
полное приращение
частные производные
![]()
![]()
![]()
Пример:
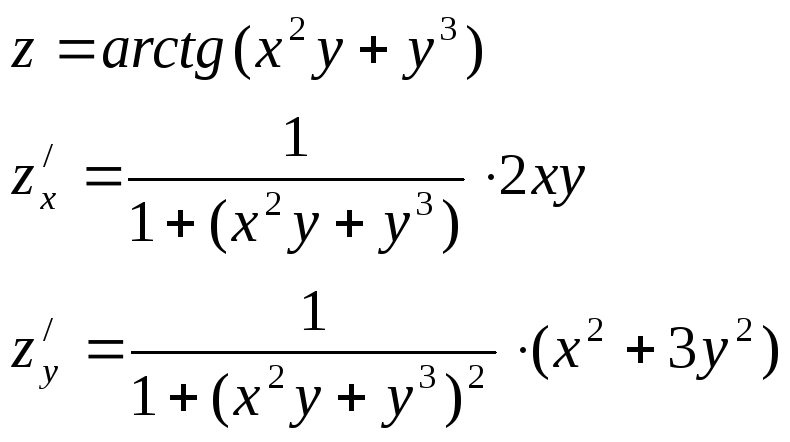
Полное приращение и полные дифференциалы.
Если полное приращение функции можно
записать в виде
![]() z=A
z=A![]() x+B
x+B![]() y+Q(
y+Q(![]()
![]() )
где
)
где![]() ,
то линейная часть уравнения (A
,
то линейная часть уравнения (A![]() x+B
x+B![]() y)
называется полным дифференциалом.
Предположим что функцияz=f(x,y)
имеет непрерывные частные производные
вU(xo,yo).
Дадим приращение независимым переменным
y)
называется полным дифференциалом.
Предположим что функцияz=f(x,y)
имеет непрерывные частные производные
вU(xo,yo).
Дадим приращение независимым переменным![]() xо
xо![]() xo+
xo+![]() x,
x,
y
![]() yo+
yo+![]() y
y![]()
![]() z=f(xo+
z=f(xo+![]() x,yo+
x,yo+![]() y)-f(xo,yo)=(f(xo+
y)-f(xo,yo)=(f(xo+![]() x,yo+
x,yo+![]() y)-f(xo,yo+
y)-f(xo,yo+![]() y))+
(f(xo,yo+
y))+
(f(xo,yo+![]() y)-f(xo,yo)=
y)-f(xo,yo)=
( по теореме Логранта
(xo+![]() x,yo+
x,yo+![]() y)
y)
![]()
![]() )
)
=![]()
![]() где
где![]()
![]() x
= dx
x
= dx
![]() y
= dy
y
= dy
![]()
f(x,y)-f(xo,yo)![]()
![]()
![]()
Свойства функции непрерывной на замкнутом множестве
Функция z=f(x,y) имеет наибольшее значение наDв точкахxo, yo если
f(xo,yo)![]() f(x,y)
f(x,y)![]()
??????????????????????????
f(xo,yo)![]() f(x,y)
f(x,y)![]()
f(x,y) непрерывна на
 то
то
![]() :
f(xo,
yo)
:
f(xo,
yo)![]() f(x,y)
f(x,y)
![]() :
f(x1,
y1)
:
f(x1,
y1)![]() f(x,y)
f(x,y)
f(x,y) непрерывна на
 то
то
M= наибольшееf(x,y)
M= наименьшееf(x,y)
![]()
![]()
![]()
Частная производная сложной функции
Z=f(u,v)
u = u(x,y)
v = v(x,y)
![]()
![]()
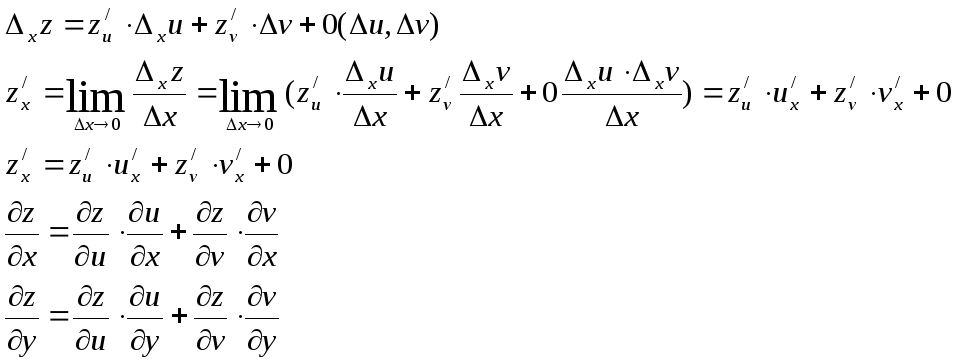
Пример

Полная производная
z=z(x,y,t)
x=x(t)
y=y(t)
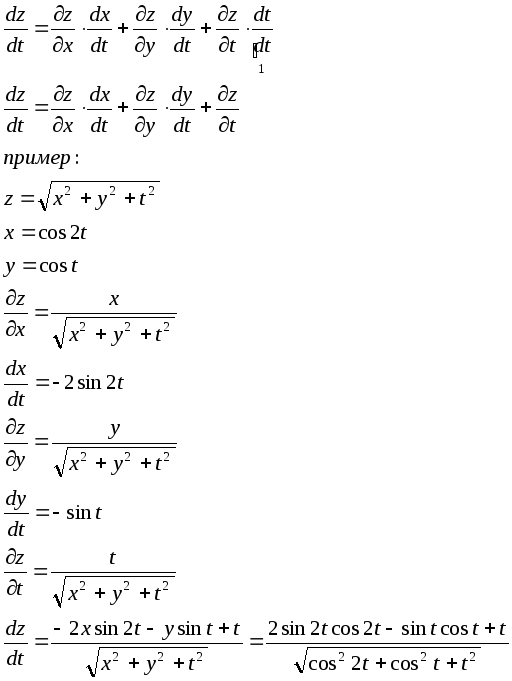
Производные неявной функции
F(x,y)=0 (*) задает неявную функцию в окрестности точки (xo,yo)
F(xo,yo)=0
Будем считать что функция Fимеет непрерывные частные производные![]() вU(xo,yo),
вU(xo,yo),![]() (xo,yo)
(xo,yo)![]()
x = xo+![]() x
x
![]() y = yo+
y = yo+![]() y
y
F(xo+![]() x,
yo+
x,
yo+![]() y)=0
y)=0
![]() F=
F(xo+
F=
F(xo+![]() x,
yo+
x,
yo+![]() y)
- F(xo,yo)=0
y)
- F(xo,yo)=0
![]()
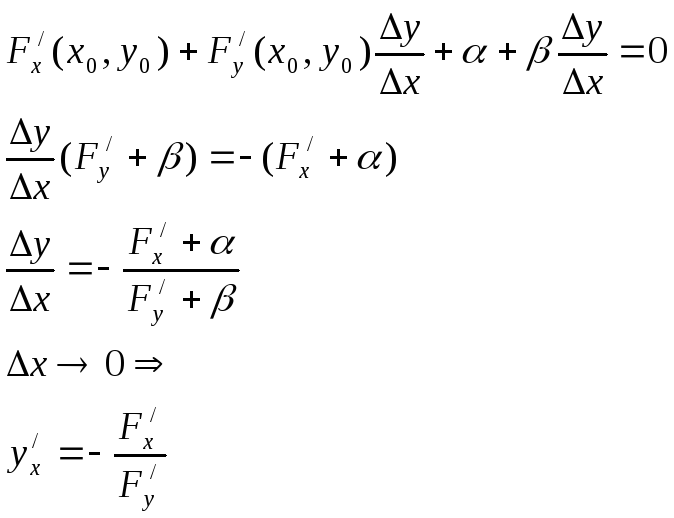
Пример
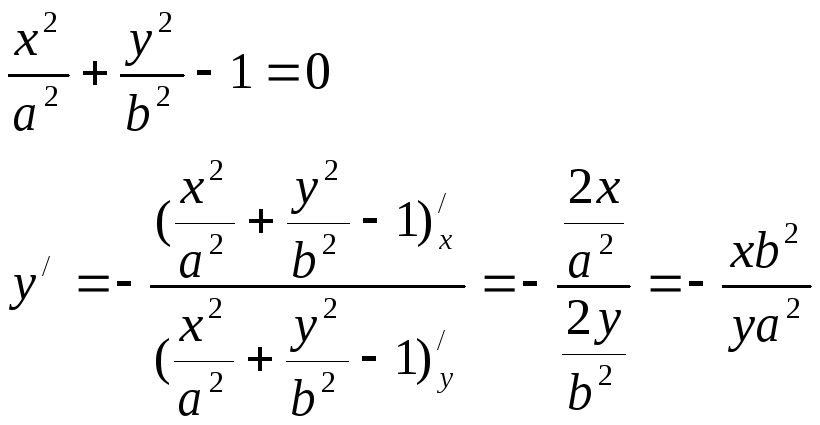
Частные производные неявной функции
F(x,y,z)=0 (**)
Z=z(x,y)
![]()
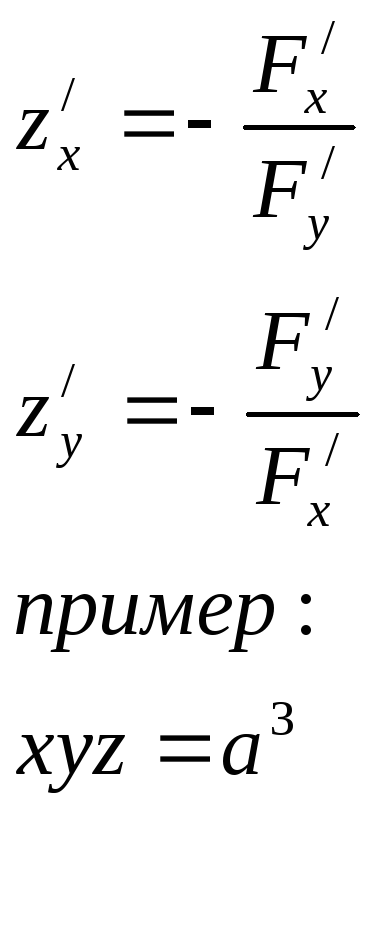
![]()
xyz-a3=0