Методы параметрического синтеза законов управления.

Методы параметрического синтеза делятся на:

- методы, ориентирующиеся на синтез параметров типовых законов управления;

- методы синтеза параметров произвольно выбранных законов.

Последние часто относятся к ММ вспомогательных управляющих устройств, называемых корректирующими устройствами.

Расчет параметров настройки типовых законов управления методом модально-параметрических ограничений.

Рисунок 7.

Используется понятие расширенных ЧХ, когда в операторных выражениях оператор Лапласа заменяют некоторым выражением

,

(4)

То есть появляется действительная часть, которая в общем случае может быть функцией частоты. Частный случай:

(5) (6)

- ограничение на колебательность.

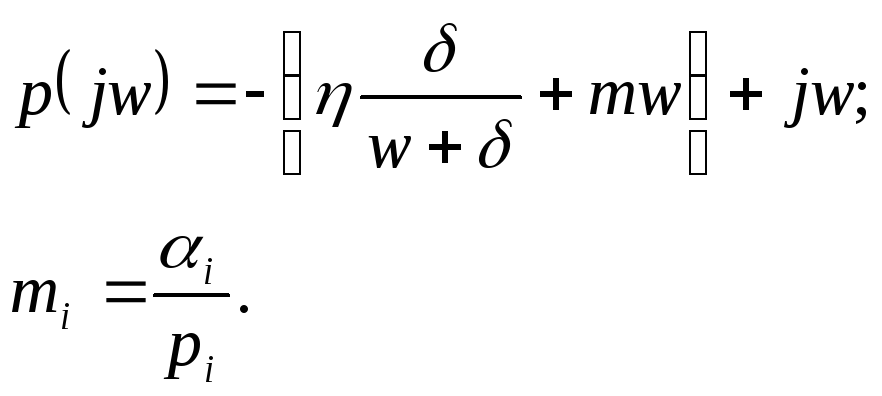
Если в ХП подставить данное выражение, то получим фигуру, описанную на рисунке 7.

Пусть задан ХП системы:

.

(7)

Если в полином подставить расширенное выражение и приравнять его к нулю, то получим характеристическое выражение 8.

.

(8)

Выражение 8 эквивалентно системе двух уравнений, в которых нулю приравнивается действительная и мнимая части характеристического комплекса.

(9)

Так как получили систему двух уравнений, то их решение – два каких-либо параметра. Одним из них обязательно должна быть частота, а вторым – один из параметров варьируемого ХП (7). Параметры ХП замкнутой системы являются функциями параметров ММ объекта, которые заданы, и ММ регулятора, то есть ЗУ, который необходимо найти.

Естественно, что при синтезе рассматриваются только те ХП, которые зависят от коэффициентов ЗУ. Таким образом в рассматриваемом методе из системы 9 можно найти только один однозначный параметр ЗУ.

Начиная со вторых параметров ЗУ и выше, решение задачи синтеза многовариантно. В случае двухпараметрического закона управления решение вырождается в бесконечное количество пар , каждая из которых соответствует некоторому произвольно фиксированному значению. В результате решением задачи синтеза является уже не точка (подпространство нулевого порядка), а линия или кривая (подпространство первого порядка), которая отображает решение в пространстве второго порядка – параметрическое пространство второго порядка.

При трех варьируемых параметрах решением является уже подпространство второго порядка (поверхность) в параметрическом пространстве третьего порядка и т.д.

Решением же задачи синтеза всегда должна быть точка в параметрическом пространстве любого порядка (координаты точки есть «настройки» системы). Поэтому для коррекции многовариантной задачи прибегают к двум кардинально различным приемам: методу волевого выбора и оптимизационному подходу. Для реализации второго метода формируются дополнительные критерии качества или предпочтительности решения и точка допустимой параметрической области, доставляющей экстремум этому критерию, является решением данной задачи - и. Известно, чем больше, тем больше его статическая и динамическая точность. Чем меньше, тем выше быстродействие. Чем больше отношениек, тем лучше для системы.

Для того, чтобы найти коэффициенты ХП, зависящие от настроечного регулятора, или ЗУ, необходимо записать выражение для характеристической функции системы (знаменатель ПФ ЗС) и находят выражение для ХП, где настроечные коэффициенты ЗУ выступают в качестве аргумента. Для более чем двухпараметрических законов выбирают те коэффициенты ХП, которые называются непрерывно варьируемыми при расчете и те коэффициенты, которые принимают дискретные фиксированные значения.