- •Тверской государственный технический университет
- •Контрольная работа
- •Фамилия, имя, отчество
- •3. Обратная матрица
- •4. Ранг матрицы
- •5. Системы линейных уравнений
- •6. Примеры
- •Тема 2. Векторная алгебра и аналитическая геометрия
- •5. Прямая на плоскости.
- •6. Угол между двумя прямыми.
- •7. Плоскость в пространстве.
- •8. Прямая в пространстве.
- •Тема 3. Введение в математический анализ. Предел последовательности
- •Предел функции
- •Некоторые эталонные пределы
- •Непрерывность функции
- •Классификация точек разрыва
- •Производная и дифференциал
- •1) 2).
- •Правило Лопиталя
- •Часть 2
Непрерывность функции
Определение.
Функция
![]() называется непрерывной в точке
называется непрерывной в точке![]() ,
если она определена в точке
,
если она определена в точке![]() и в некоторой окрестности точки
и в некоторой окрестности точки![]() и если
и если![]() .
.
Геометрически
непрерывность функции в данной точке
означает, что разность ординат графика
функции
![]() в точках
в точках![]() и
и![]() будет мала, если
будет мала, если![]() достаточно мало.
достаточно мало.
Определение.
Если функция
![]() непрерывна в каждой точке интервала
непрерывна в каждой точке интервала![]() ,
то она непрерывна на этом интервале.
,
то она непрерывна на этом интервале.
Если функция
определена при
![]() и при этом
и при этом![]() ,
то говорят, что функция
,
то говорят, что функция![]() непрерывна в точке
непрерывна в точке![]() справа.
справа.
Если функция
определена при
![]() и при этом
и при этом![]() ,
то говорят, что функция
,
то говорят, что функция![]() непрерывна в точке
непрерывна в точке![]() слева.
слева.
Если функция
непрерывна на интервале
![]() ,
и непрерывна в точках
,
и непрерывна в точках![]() соответственно справа и слева, то функция
непрерывна на отрезке
соответственно справа и слева, то функция
непрерывна на отрезке![]() .
.
Если в точке
![]() для функции
для функции![]() не выполняется какое-либо условие
непрерывности, т.е. функция не определена
в точке
не выполняется какое-либо условие
непрерывности, т.е. функция не определена
в точке![]() или не существует
или не существует ,
или
,
или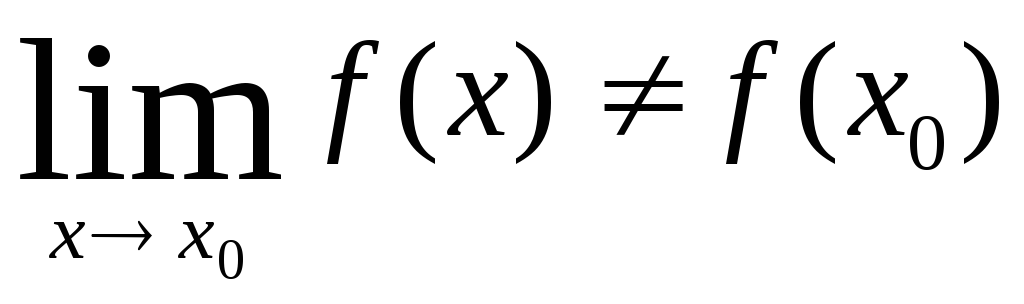 ,
то функция
,
то функция![]() разрывна при
разрывна при![]() .
Точка
.
Точка![]() называется точкой разрыва.
называется точкой разрыва.
Теорема. Всякая элементарная функция непрерывна на своей области определения.
Классификация точек разрыва
Точка
![]() функции
функции![]() называется точкой разрываI
рода, если существуют конечные
односторонние пределы
называется точкой разрываI
рода, если существуют конечные
односторонние пределы
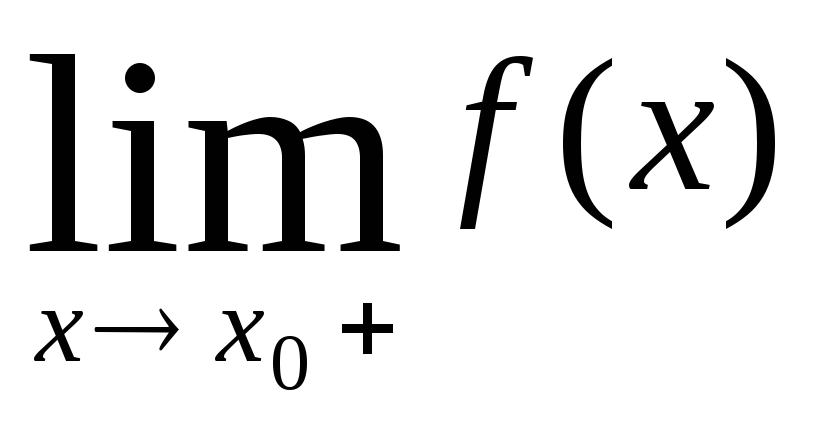 и
и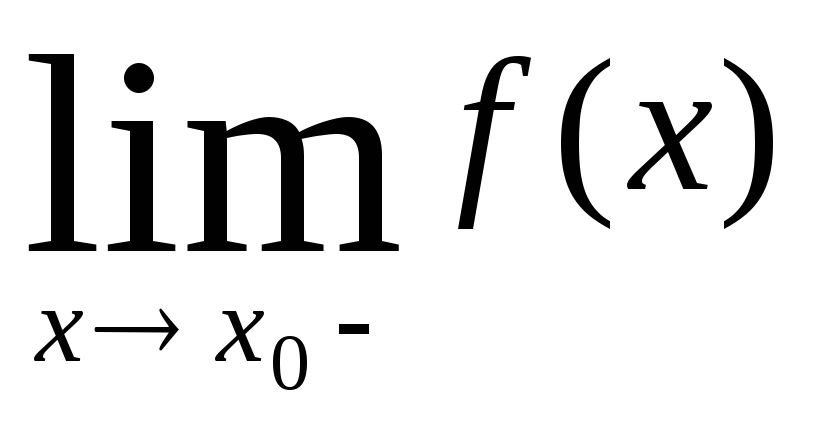 .
.
Точка разрыва I
рода называется устранимой, если
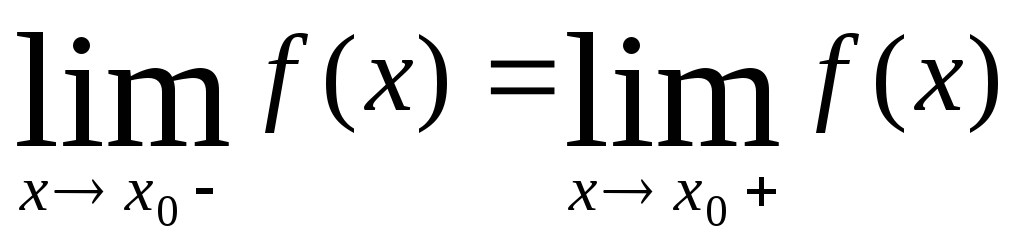 .
.
Если односторонние
пределы конечны, но не совпадают, то
![]() - неустранимая точка разрыва.
- неустранимая точка разрыва.
Точка
![]() функции
функции![]() называется точкой разрываII
рода, если хотя бы один из односторонних
пределов бесконечен или не существует.
называется точкой разрываII
рода, если хотя бы один из односторонних
пределов бесконечен или не существует.
П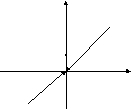 римеры.
римеры.
1.
![]() .y
.y
![]() ;
1
;
1
![]() .
x
.
x
![]()
![]() - точка разрыва
- точка разрыва
I рода устранимая.
 y
y
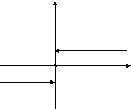
2.
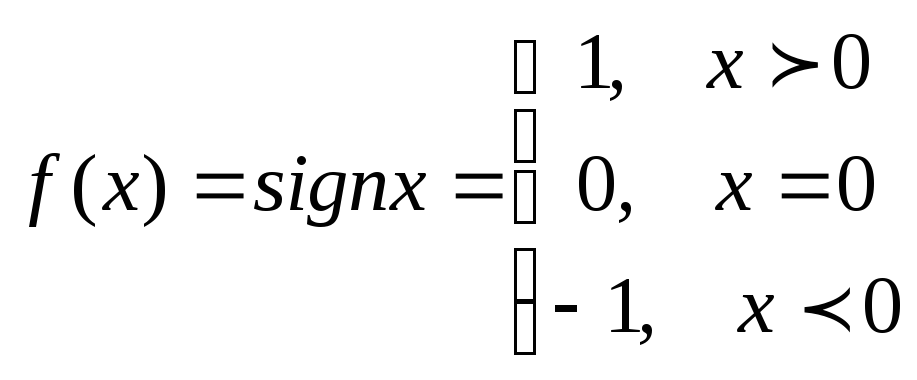 .
1
.
1
0 x
![]() ;
;
![]()
![]() - точка разрыва I
рода неустранимая.
- точка разрыва I
рода неустранимая.
3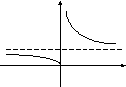 .y
.y
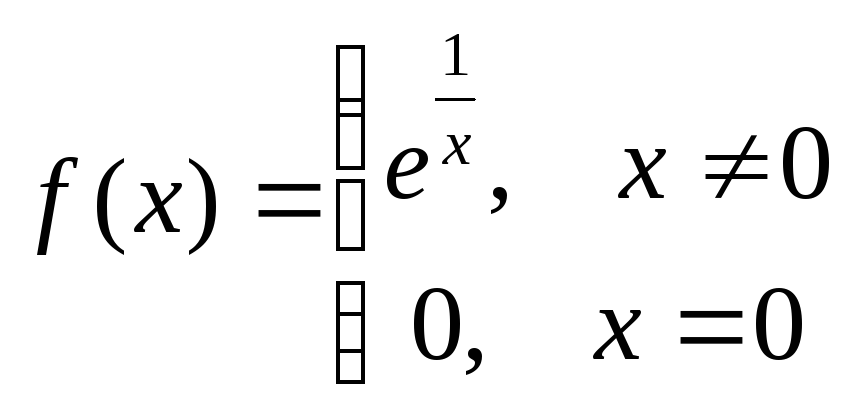 .
.
![]() ;
0
;
0
![]()
![]() -точка разрыва II
рода.
-точка разрыва II
рода.
4. Исследовать на непрерывность функцию
y=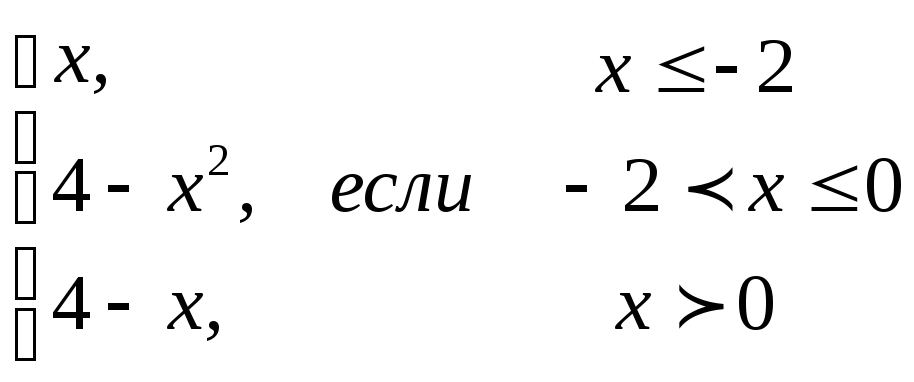 .
.
Естественно, что на интервалах (-∞;-2), (-2;0) и (0;+∞) функция непрерывна. Проверке подлежат только точки х = -2 и х = 0.
Для того чтобы убедиться, что функция непрерывна в точке, требуется проверить, равны ли между собой односторонние пределы и равны ли они значению функции в этой точке.
Рассмотрим точку х = -2.
![]() .
.
Вычислим односторонние пределы:
![]()
![]()
![]()
![]() .
.
Так как односторонние пределы не совпадают, х = -2 - точка разрыва функции I рода неустранимая.
Рассмотрим точку х = 0.
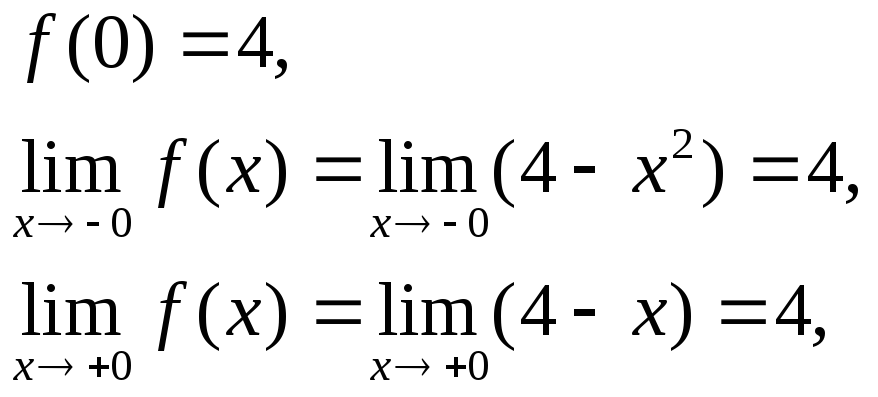
x = 0 - точка непрерывности функции, выполнены все условия непрерывности.

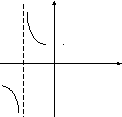
5. Исследовать поведение функции вблизи точки разрыва. Построить схематический чертеж.
![]() .
.
Решение. Область определения функции
![]()
Точка разрыва х = -10.
Найдем односторонние пределы:
![]()
![]()
Знак предела
зависит от знаков числителя и знаменателя
дроби. В обоих случаях числитель (2х
+ 5)![]() -15,
но знаменатель в пределе слева остается
отрицательным, приближаясь к нулю, а в
пределе справа, приближаясь к нулю,
знаменатель остается положительным.
Схематичный чертеж представлен на
рисунке.
-15,
но знаменатель в пределе слева остается
отрицательным, приближаясь к нулю, а в
пределе справа, приближаясь к нулю,
знаменатель остается положительным.
Схематичный чертеж представлен на
рисунке.