
- •Тверской государственный технический университет
- •Контрольная работа
- •Фамилия, имя, отчество
- •3. Обратная матрица
- •4. Ранг матрицы
- •5. Системы линейных уравнений
- •6. Примеры
- •Тема 2. Векторная алгебра и аналитическая геометрия
- •5. Прямая на плоскости.
- •6. Угол между двумя прямыми.
- •7. Плоскость в пространстве.
- •8. Прямая в пространстве.
- •Тема 3. Введение в математический анализ. Предел последовательности
- •Предел функции
- •Некоторые эталонные пределы
- •Непрерывность функции
- •Классификация точек разрыва
- •Производная и дифференциал
- •1) 2).
- •Правило Лопиталя
- •Часть 2
6. Примеры
Даны матрицы
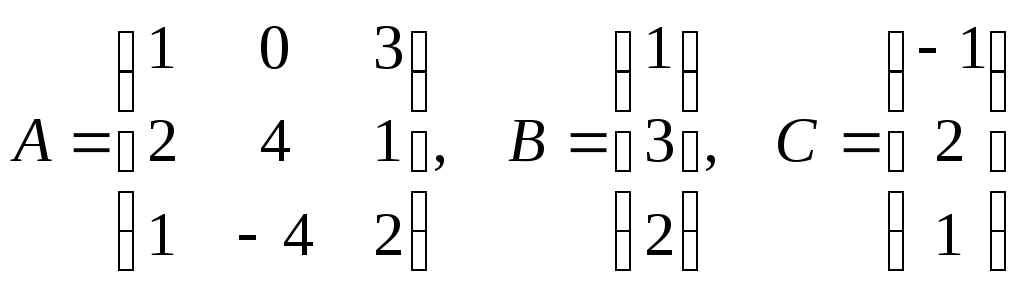 и число
и число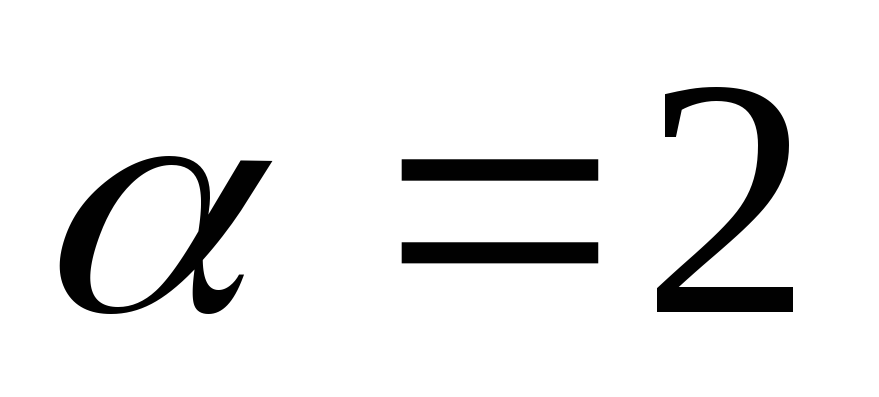 .
Найти
.
Найти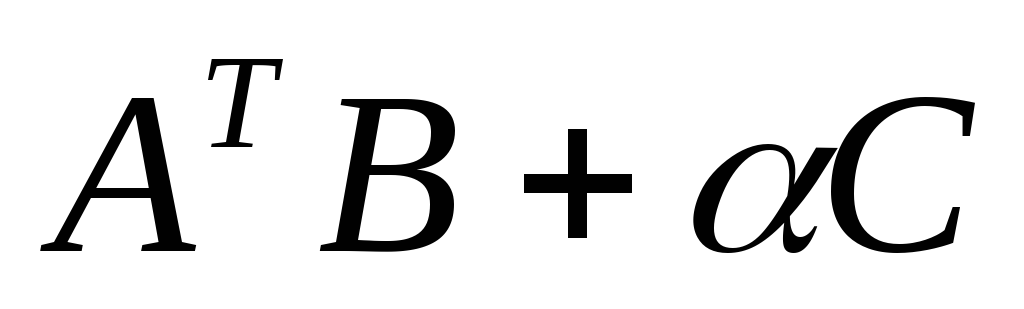 .
.

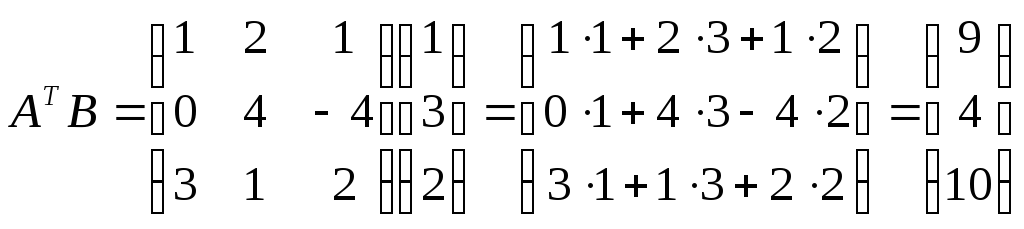
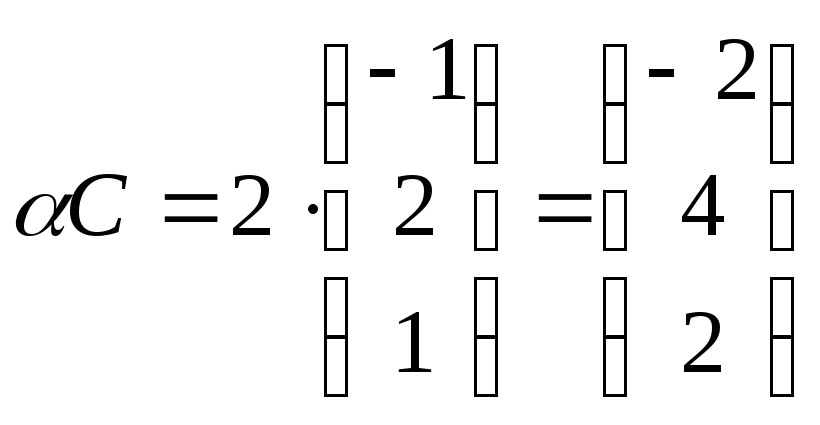

Дана матрица
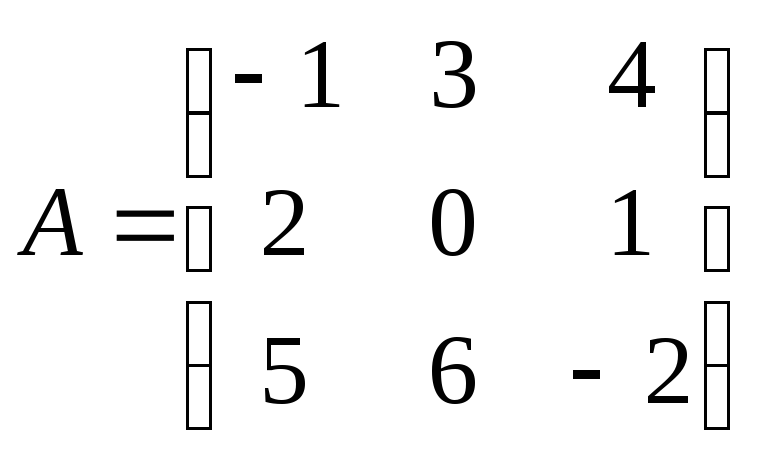 .
Найти
.
Найти .
.
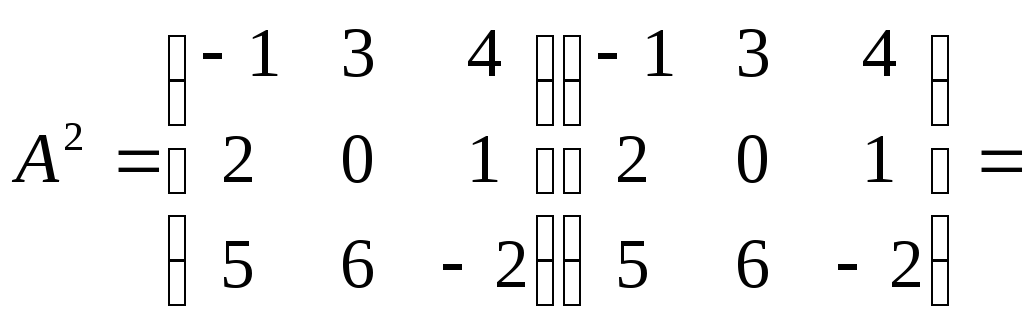

Даны матрицы
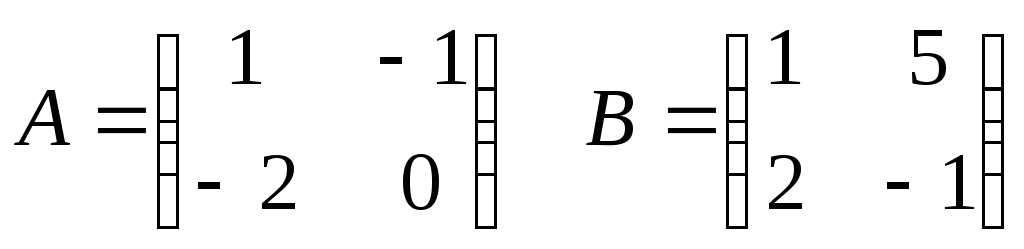
Найдите
![]()
I способ.
![]()
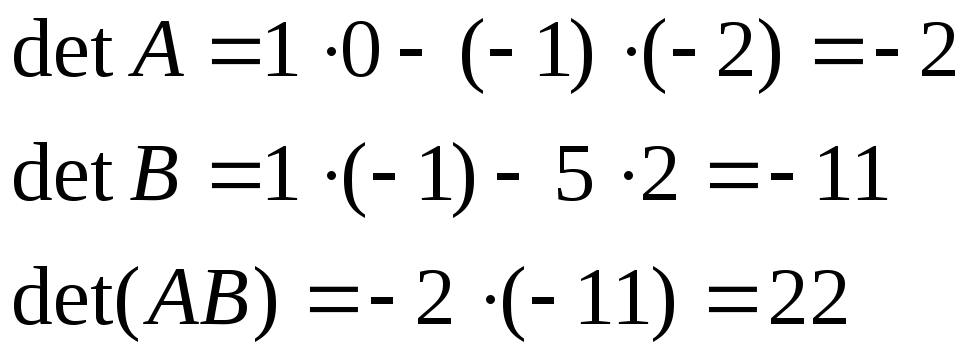
II способ.
![]()
![]()
Вычислить определитель

Вычислим определитель различными способами:
по правилу треугольников

разложим определитель по первой строке
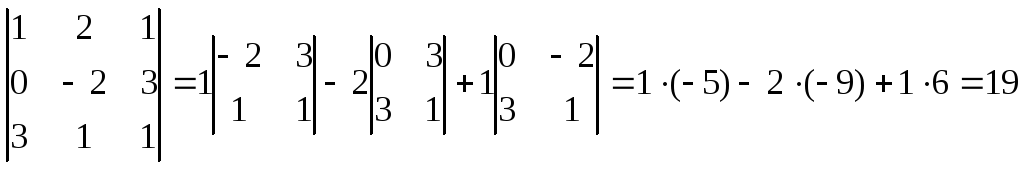
приведём определитель к треугольному виду

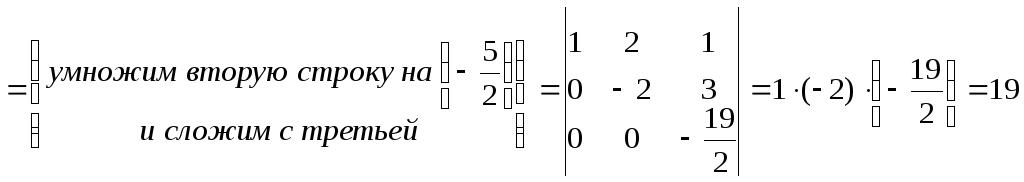
Вычислить определитель
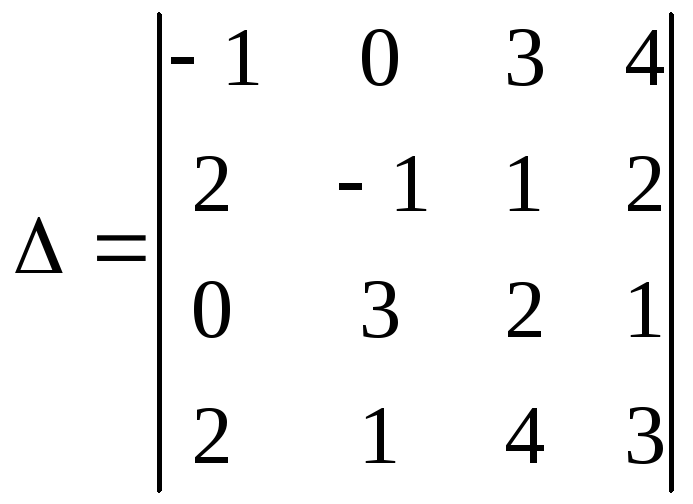
I способ.
Лучше разложить данный определитель по строке или столбцу, содержащим нули, т.к. наличие нуля уменьшает вычисления. Выберем, например, второй столбец.




![]()
II способ.


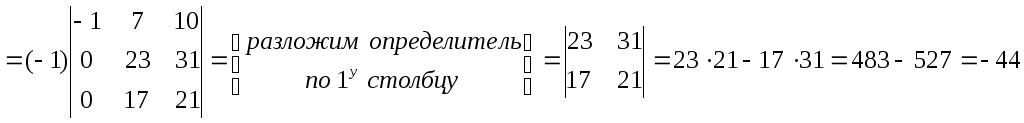
Найти
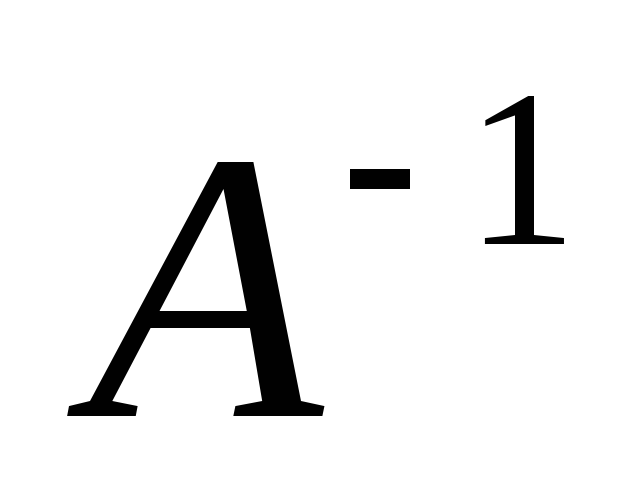 ,
если
,
если .
Сделать проверку.
.
Сделать проверку.
1)
![]() ,
значит существует
,
значит существует![]() .
.
2) Найдём алгебраические дополнения
![]()
![]()
![]()
3)
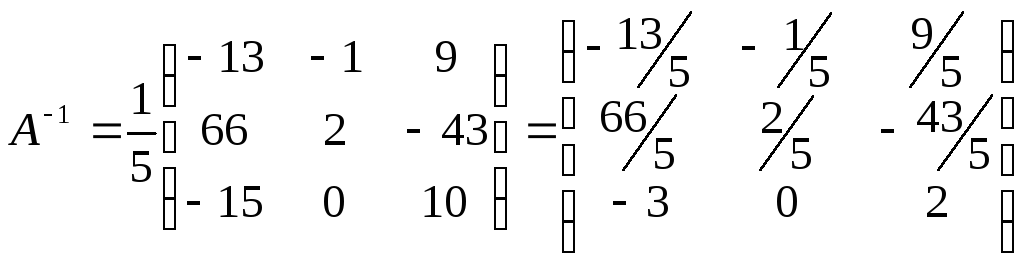
4) Проверка


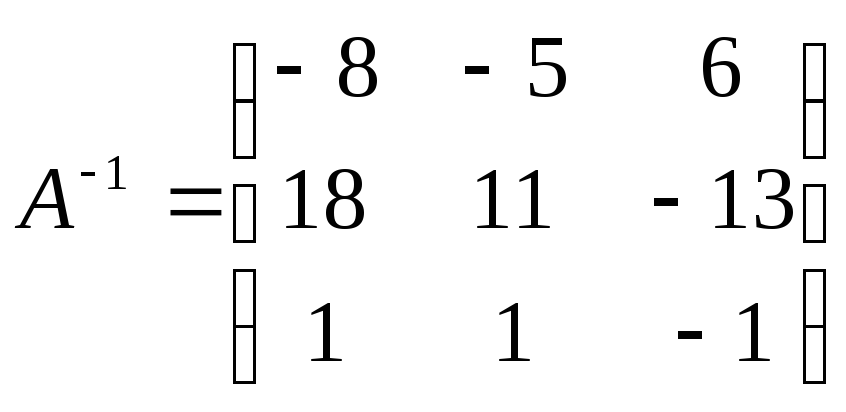
Методом элементарных преобразований найти
 для матрицы
для матрицы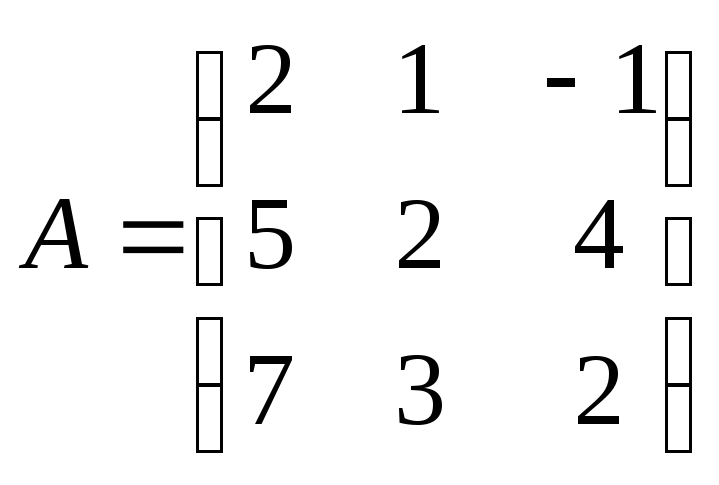


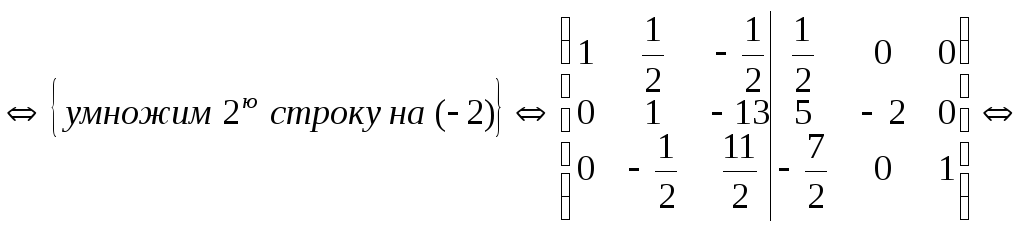

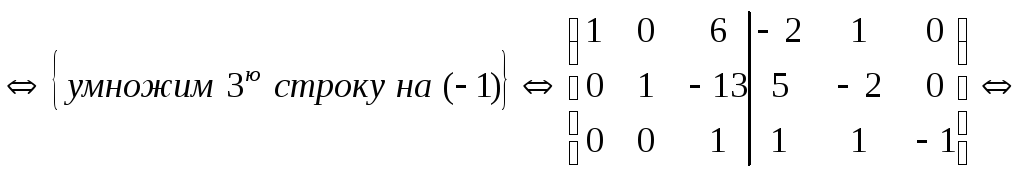

Найти ранг матрицы





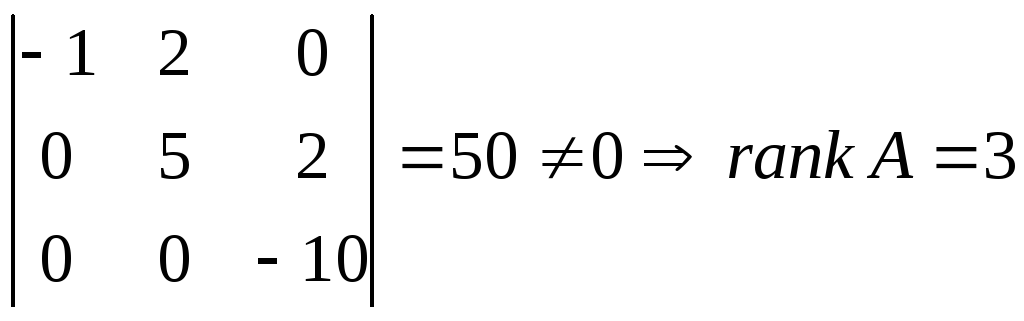
Решить систему уравнений

а) методом Крамера
б) матричным способом
в) методом Гаусса
а)
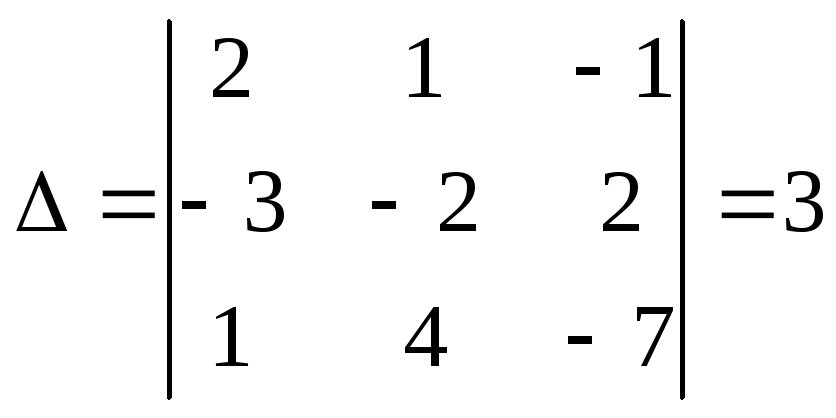
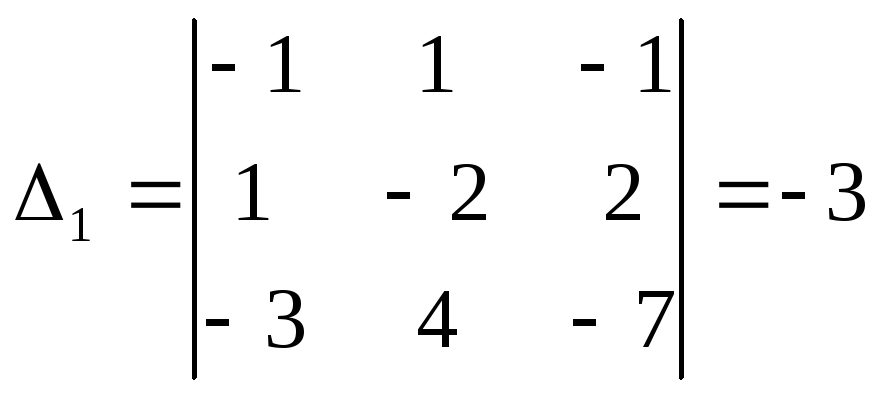
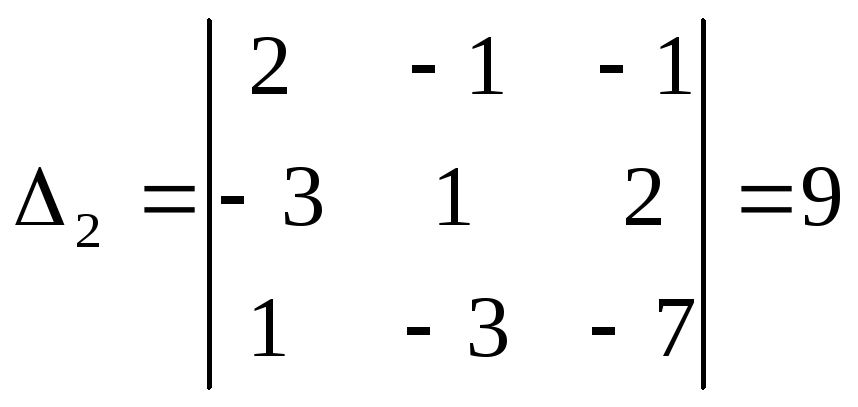
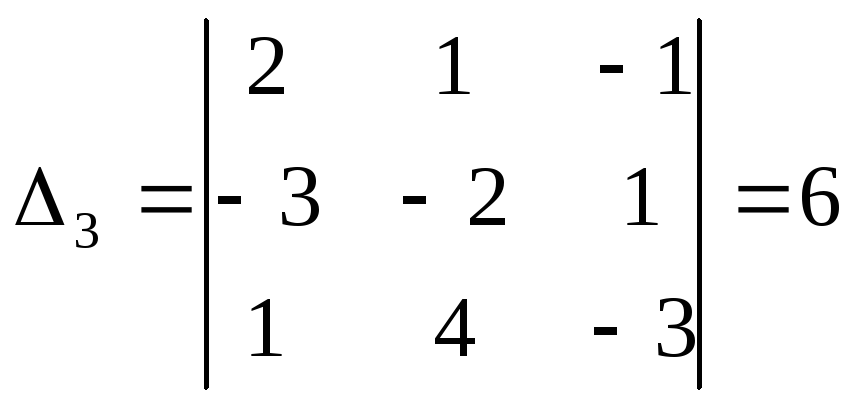
![]()
б)
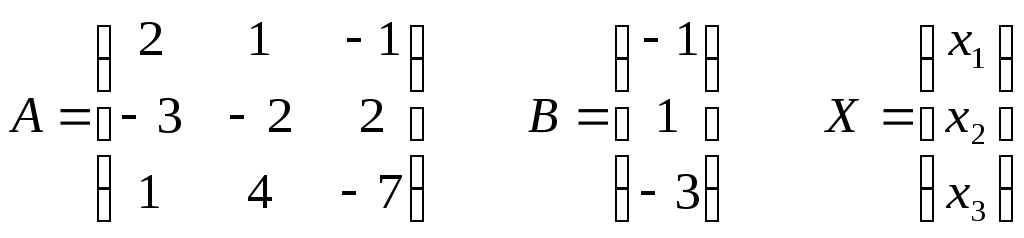
![]() существует
существует
![]()
Найдём
![]() .
.
![]()
![]()
![]()

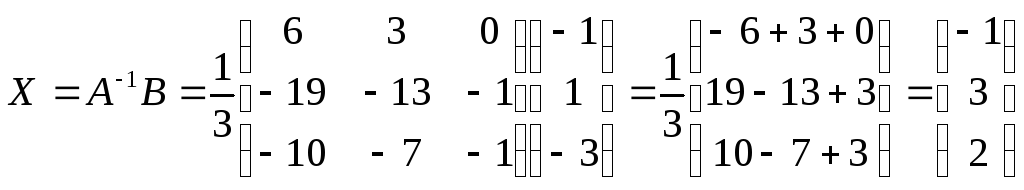
в)



По данной матрице запишем систему уравнений
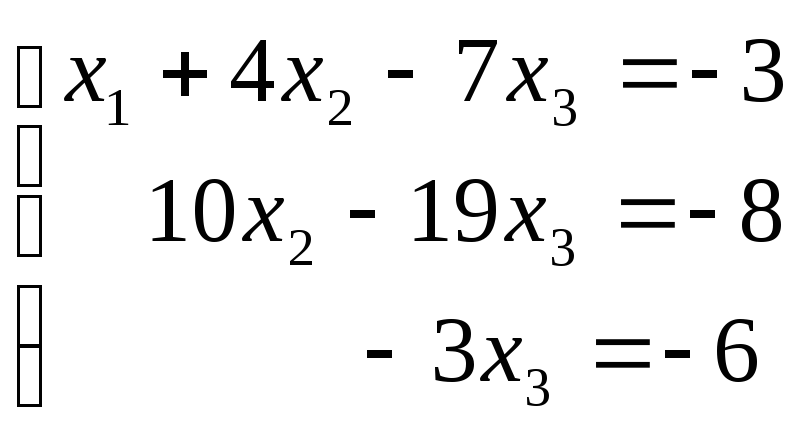
Из последнего
уравнения найдём
![]() ,
подставим его во второе уравнение,
найдём
,
подставим его во второе уравнение,
найдём![]() ,
а затем из первого найдём
,
а затем из первого найдём![]() .
.
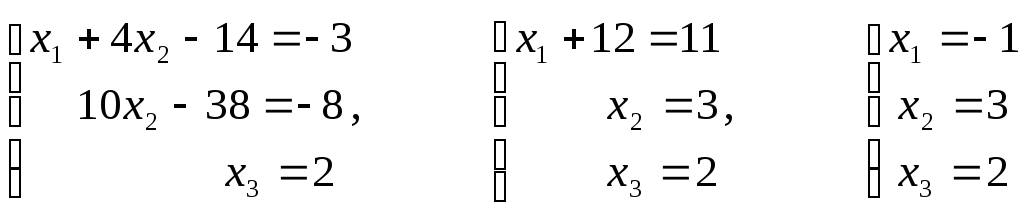
Определить совместность системы


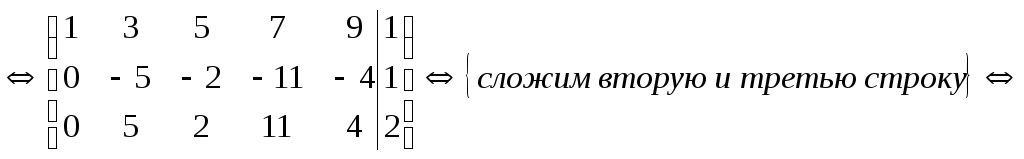
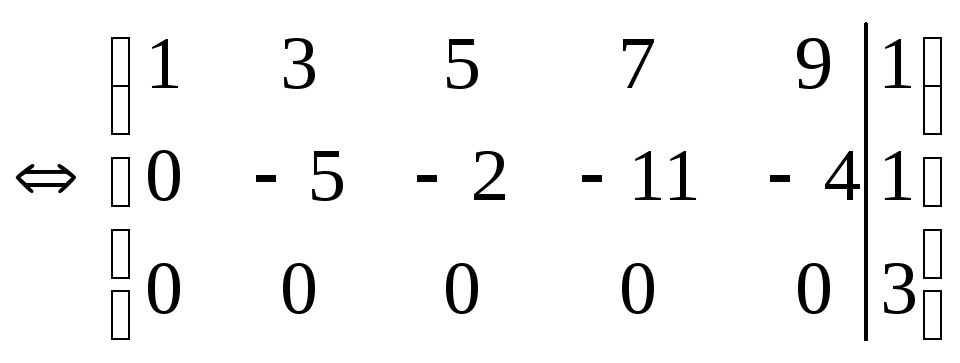
Ранг матрицы коэффициентов равен 2. Ранг расширенной матрицы равен 3. Следовательно, система несовместна.
Решить систему уравнений
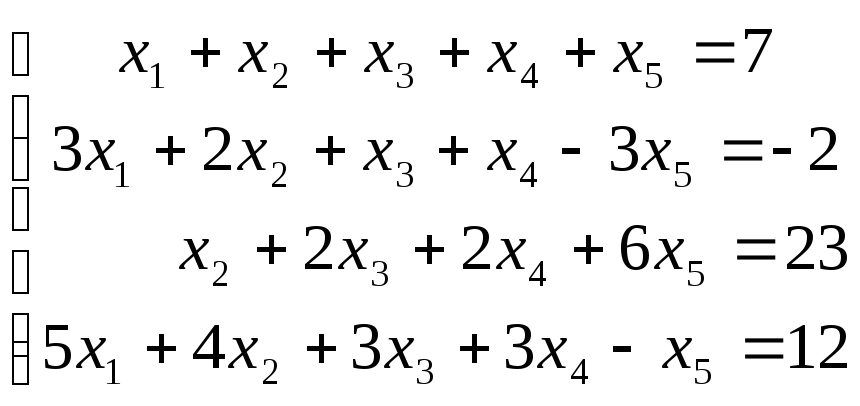


![]()
Матрица приведена
к трапецеидальному виду, под главной
диагональю элемент равен нулю. Полученная
матрица является расширенной матрицей
системы, равносильной исходной. Ранг
этой матрицы совпадает с рангом исходной.
Поэтому заключаем, что система совместна,
т.к. ранг матрицы коэффициентов равен
рангу расширенной матрицы и равен 2.
Система будет иметь
![]() свободных
неизвестных и 2 базисных.
свободных
неизвестных и 2 базисных.
Пусть
![]() -
базисные переменные,
-
базисные переменные,
![]() -
свободные
-
свободные
Тогда
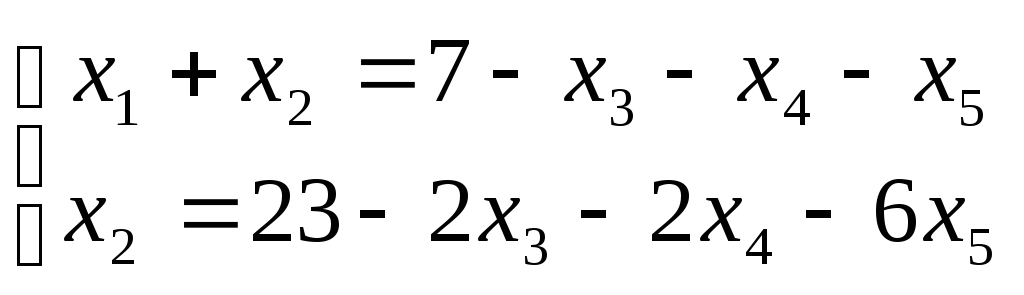
Выразим
![]() из первого равенства через свободные
из первого равенства через свободные
![]()
Общее решение может быть записано в виде
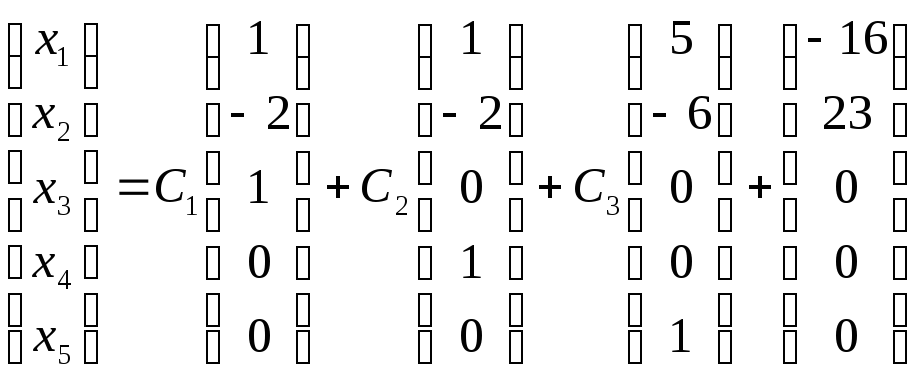
Замечание. Поскольку существует свобода выбора базисных и свободных переменных, то общее решение может быть записано в различных, но естественно, равносильных формах.
Решить систему уравнений.




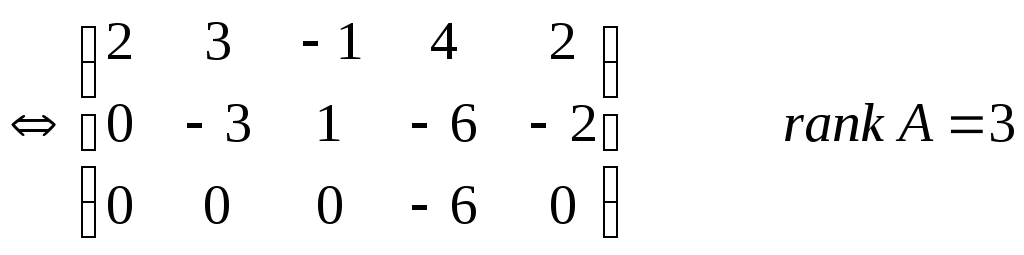
Запишем систему
уравнений
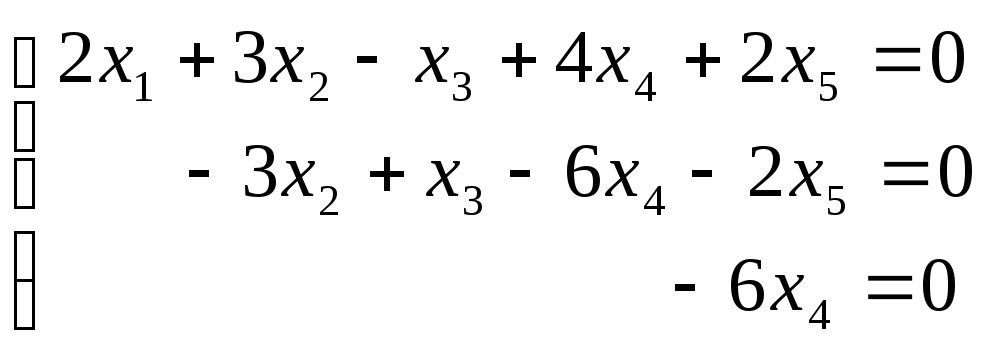
Из последнего
уравнения
![]() .
Так как
.
Так как![]() ,
то в системе 3 базисные переменные и 2
свободные. Так как
,
то в системе 3 базисные переменные и 2
свободные. Так как![]() однозначно определена, то она базисная
и пусть
однозначно определена, то она базисная
и пусть![]() и
и![]() - тоже базисные. Тогда
- тоже базисные. Тогда![]() - свободные. (За базисные неизвестные
необходимо выбирать такие, при которых
матрица коэффициентов не вырождена).
- свободные. (За базисные неизвестные
необходимо выбирать такие, при которых
матрица коэффициентов не вырождена).
Выразим
![]() из второго уравнения через
из второго уравнения через![]()
![]()
Из первого уравнения
найдём
![]()
![]() .
.
Тогда общее решение системы имеет вид
![]() ,
где
,
где
![]()
Обозначим

Эти векторы образуют фундаментальную систему решений.
Любое решение
системы запишется в виде
![]()
Тема 2. Векторная алгебра и аналитическая геометрия
Векторы. Основные определения.
Вектором называется направленный отрезок. К векторам относится также нулевой вектор, начало и конец которого совпадают. Вектор характеризуется своей длиной (модулем) и направлением.
 B
B
![]()
A
Линейные операции над векторами:
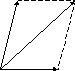
1). Сложение векторов.
![]()
![]()
![]()
![]()
![]()
![]()
Складывают два вектора по правилу параллелограмма или треугольника. Правило треугольника можно обобщить на n-слагаемых. Если каждый раз соединять начало последующего вектора с концом предыдущего, то получим ломаную линию. Вектор, соединяющий начало первого с концом последнего и есть сумма.
2). Умножение вектора на число.
При умножении
вектора
![]() на число
на число![]() его модуль увеличивается (если
его модуль увеличивается (если![]() )
или уменьшается (если
)
или уменьшается (если![]() )
в
)
в![]() раз, а направление не изменяется, если
раз, а направление не изменяется, если![]() и меняется на противоположное, если
и меняется на противоположное, если![]() .
.
В любом случае
векторы
![]() и
и![]() лежат на одной прямой или на параллельных
прямых. Такие векторы называютсяколлинеарные.
лежат на одной прямой или на параллельных
прямых. Такие векторы называютсяколлинеарные.
Нулевой вектор считается коллинеарным любому вектору.
Векторы, лежащие в одной плоскости или в параллельных плоскостях, называются компланарными.
Свойства линейных операций:
1). Коммутативность
![]()
2). Ассоциативность
![]() ,
,
![]()
3). Дистрибутивность
![]()
![]() ,
где
,
где
![]()
Рассмотрим систему
векторов
![]() .
Выражение вида
.
Выражение вида![]() ,
где
,
где![]() называется линейной комбинацией векторов
называется линейной комбинацией векторов![]() .
Если в линейной комбинации все
.
Если в линейной комбинации все![]() ,
то система векторов линейно независима.
Если существуют
,
то система векторов линейно независима.
Если существуют![]() ,
то система – линейно зависима.
,
то система – линейно зависима.
Любая упорядоченная
линейно независимая тройка векторов
![]() называетсябазисом
в пространстве. Векторы
называетсябазисом
в пространстве. Векторы
![]() называютсябазисными.
Если базисные вектора взаимно
перпендикулярны, то базис называется
ортогональным.
Если базисные векторы имеют единичную
длину, то они называются ортами.
Базис называется ортонормированным,
если базисные векторы единичные и
взаимно перпендикулярные. Декартова
система координат – ортонормированная,
орты прямоугольной декартовой системы
координат обозначают
называютсябазисными.
Если базисные вектора взаимно
перпендикулярны, то базис называется
ортогональным.
Если базисные векторы имеют единичную
длину, то они называются ортами.
Базис называется ортонормированным,
если базисные векторы единичные и
взаимно перпендикулярные. Декартова
система координат – ортонормированная,
орты прямоугольной декартовой системы
координат обозначают
![]() .
.
Пусть
![]() - некоторый базис в пространстве. Пусть
- некоторый базис в пространстве. Пусть![]() - произвольный вектор пространства.
Рассмотрим линейную комбинацию
- произвольный вектор пространства.
Рассмотрим линейную комбинацию
![]()
Так как любая четвёрка векторов линейно зависима, то не все коэффициенты линейной комбинации равны 0.
![]()
Эта формула даёт
разложение вектора
![]() по базису (
по базису (![]() ).
Коэффициенты
).
Коэффициенты![]() - координаты вектора
- координаты вектора![]() в этом базисе. Разложение вектора по
базису единственное, т.е. координаты
вектора однозначно определяют сам
вектор.
в этом базисе. Разложение вектора по
базису единственное, т.е. координаты
вектора однозначно определяют сам
вектор.
В связи с этим можно записать следующие свойства:
Пусть даны векторы
![]() и
и![]()
1). Равные векторы
имеют одинаковые координаты, т.е. если
![]() ,
то
,
то![]() .
.
2). При умножении
вектора на число, его координаты
умножаются на это число
![]() .
.
3). При сложении
двух векторов складываются их
соответствующие координаты
![]() .
.
Проекцией вектора
![]() на вектор
на вектор![]() называется число
называется число![]() ,
где
,
где![]() .
.
Координаты вектора
![]() в прямоугольном базисе совпадают с
проекциями вектора
в прямоугольном базисе совпадают с
проекциями вектора![]() на базисные орты
на базисные орты![]() ,
а длина вектора равна
,
а длина вектора равна
![]()
Числа
![]()
![]()
![]()
называются
направляющими косинусами вектора
![]() .
.
Скалярное произведение.
Скалярным
произведением двух векторов
![]() и
и![]() называют число равное
называют число равное![]() ,
где
,
где![]() - угол между векторами
- угол между векторами![]() и
и![]() .
.
Свойства скалярного произведения:
1).
![]()
2).
![]()
3).
![]()
4).
![]()
Если известны
координаты векторов
![]() ,
,![]() ,
то скалярное произведение можно найти
по формуле:
,
то скалярное произведение можно найти
по формуле:
![]()
Скалярный квадрат вектора вычисляют по формуле:
![]()
Геометрические свойства скалярного произведения:
1).
![]()
2). Если
![]() ,
если
,
если![]()
3). Формула для определения угла между векторами:
![]()
Векторное произведение.
Упорядоченная
тройка некомпланарных векторов
![]() называетсяправой,
если поворот вектора
называетсяправой,
если поворот вектора
![]() к вектору
к вектору![]() на наименьший угол в плоскости векторов
на наименьший угол в плоскости векторов![]() и
и![]() виден из конца вектора
виден из конца вектора![]() происходящим против движения часовой
стрелки.
происходящим против движения часовой
стрелки.
В случае, если поворот по часовой стрелке, тройка называется левой.


![]()
![]()
![]()
![]()
![]()
![]()
Векторным
произведением
![]() называется вектор
называется вектор![]() ,
определяемый следующими условиями:
,
определяемый следующими условиями:
1). Тройка векторов
![]() правая
правая
2). Вектор
![]() перпендикулярен
перпендикулярен![]() и
и![]()
3). Длина вектора
![]() равна площади параллелограмма,
построенного на векторах
равна площади параллелограмма,
построенного на векторах![]() и
и![]() ,
т.е.
,
т.е.
![]()
Из определения векторного произведения следует, что
![]()
Свойства векторного произведения:
1).
![]()
2).
![]()
3).
![]()
4).
![]()
В координатной форме векторное произведение вычисляется по формуле:
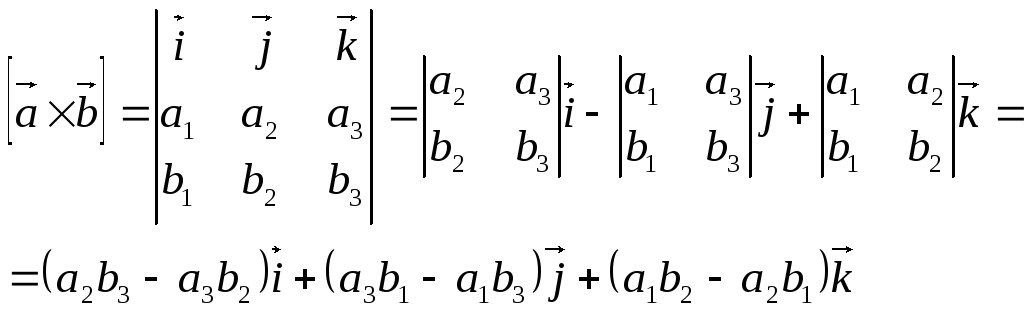
Смешанное произведение.
Смешанным
произведением трёх векторов называют
число равное
![]() .
.
Геометрические свойства:
1). Если V
– объём параллелепипеда, построенного
на векторах
![]() ,
то
,
то![]() .
Если
.
Если![]() - правая тройка, то
- правая тройка, то![]() ,
если левая, то
,
если левая, то![]() .
.
2). Вектора
![]() компланарны тогда и только тогда, когда
их смешанное произведение равно 0.
компланарны тогда и только тогда, когда
их смешанное произведение равно 0.
Основное алгебраическое свойство смешанного произведения состоит в том, что циклическая перестановка не меняет его величины, т.е.
![]()
Это свойство позволяет ввести обозначение:
![]()
(результат не зависит от того, как расставить скобки в правой части)
Смешанное произведение через координаты записывается в виде:
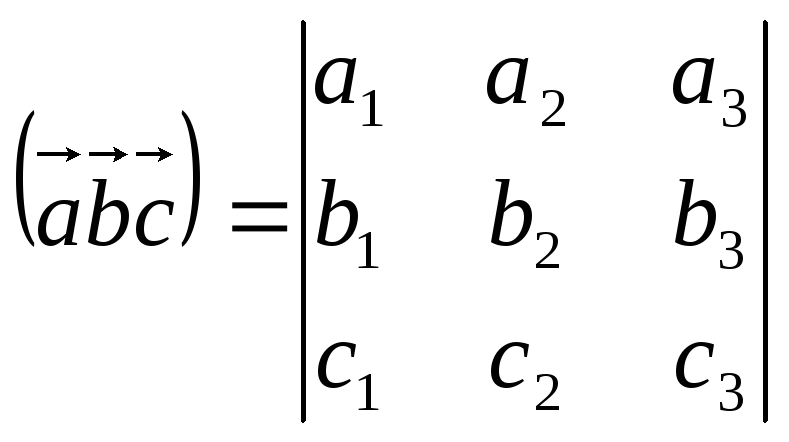
Примеры:
Доказать, что векторы
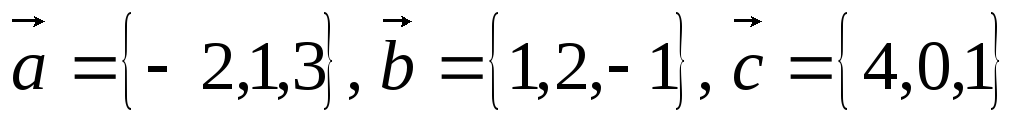 образуют базис и найти разложение
вектора
образуют базис и найти разложение
вектора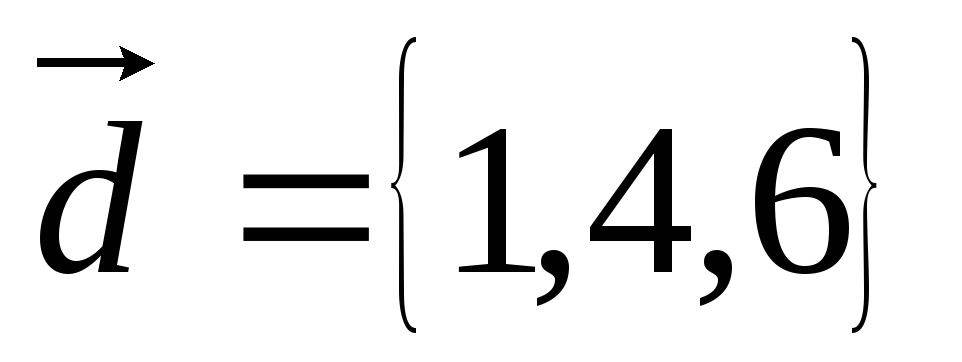 в этом базисе.
в этом базисе.
Решение: Векторы в пространстве образуют базис, если они не- компланарны. Найдём смешанное произведение этих векторов.

Следовательно,
векторы
![]() образуют базис. Пусть вектор
образуют базис. Пусть вектор![]() имеет в этом базисе координаты
имеет в этом базисе координаты![]() .
.
Тогда
![]() .
.
![]()
![]()
Два вектора равны, если равны их соответствующие координаты.
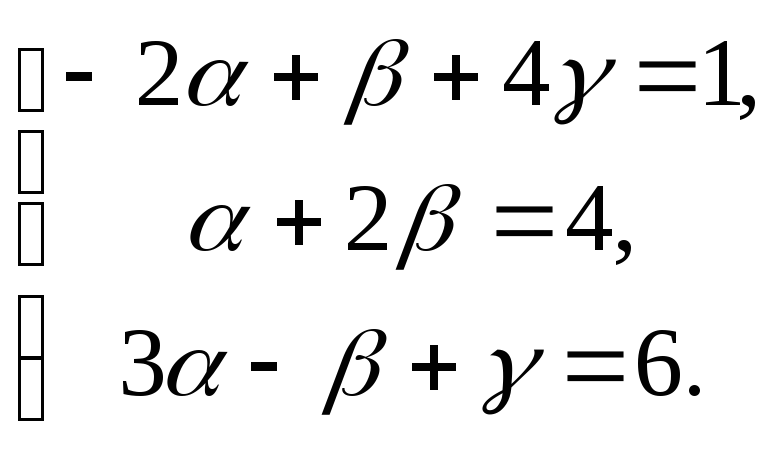
Решив эту систему,
найдём
![]() .
.
Таким образом,
![]() .
.
Даны точки
 .
.
Найти: а). длину отрезка АВ,
б).
![]() в
в![]() ,
,
в).
![]() ,
,
г). направляющие
![]() и единичный вектор направления
и единичный вектор направления![]() .
.
Решение:
а).
![]()
![]()
б). угол
B
в
![]() есть угол между векторами
есть угол между векторами
![]() и
и![]() .
.
![]()
![]()
![]()
в).
![]()
![]()
![]()
г).
![]()
Направляющие
![]() .
.
Найти
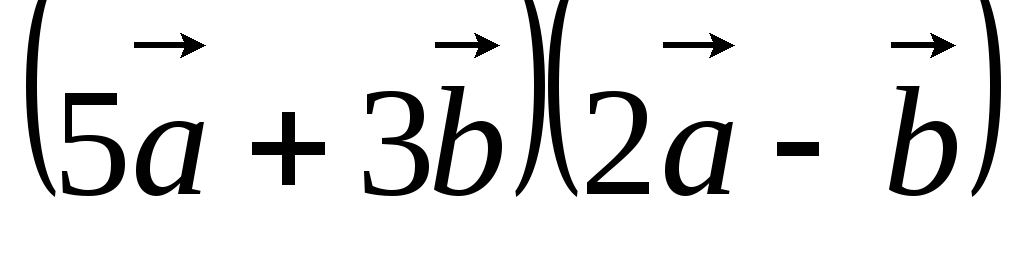 ,
если
,
если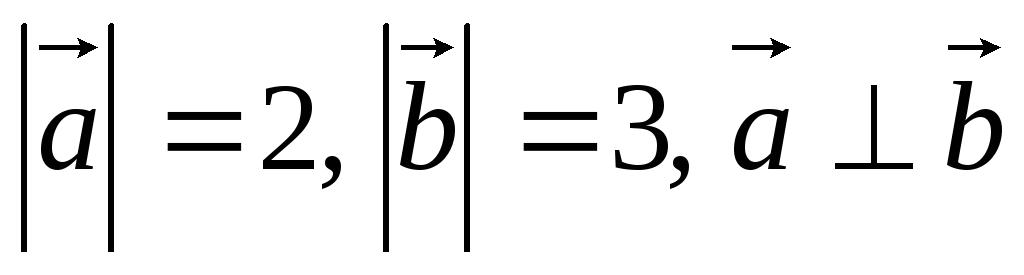 .
.
Решение:
![]()
![]() .
.
При каком
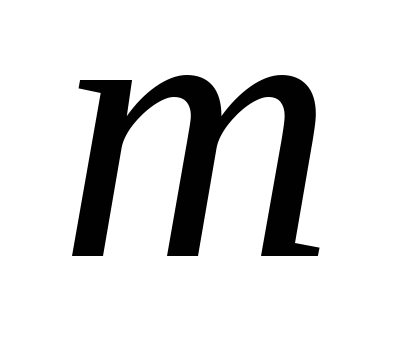 векторы
векторы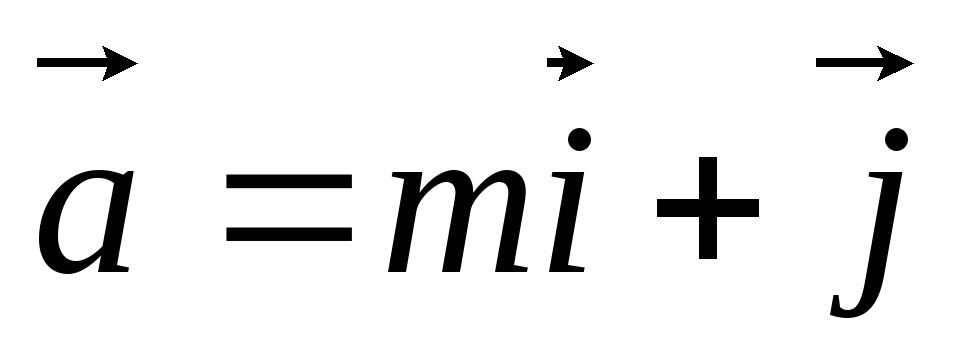 и
и перпендикулярны?
перпендикулярны?
Решение:
![]()
Если векторы перпендикулярны, то их скалярное произведение равно нулю.
![]() .
.
Найти угол между векторами
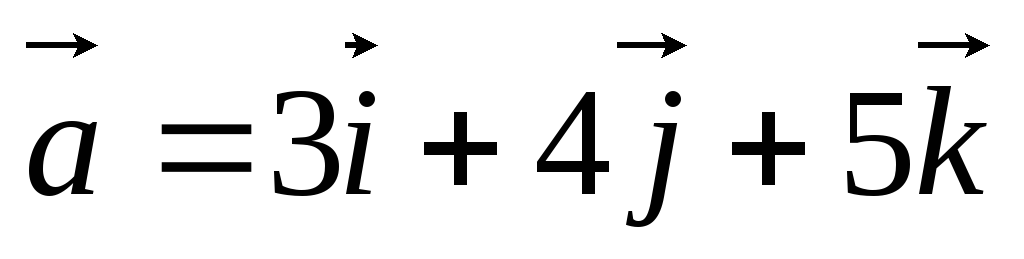 и
и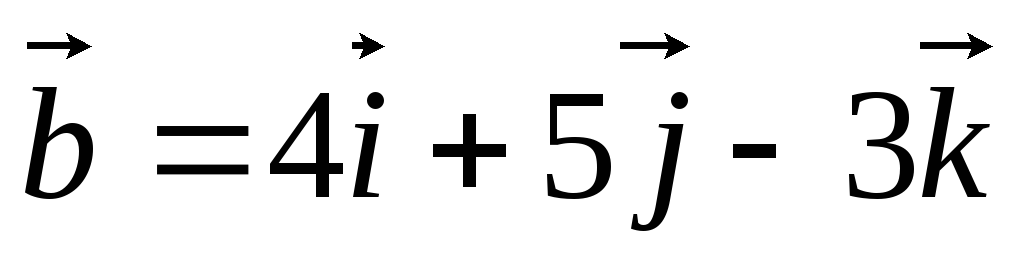 .
.
![]()
![]()
![]() .
.
Найти угол между векторами
 и
и ,
где
,
где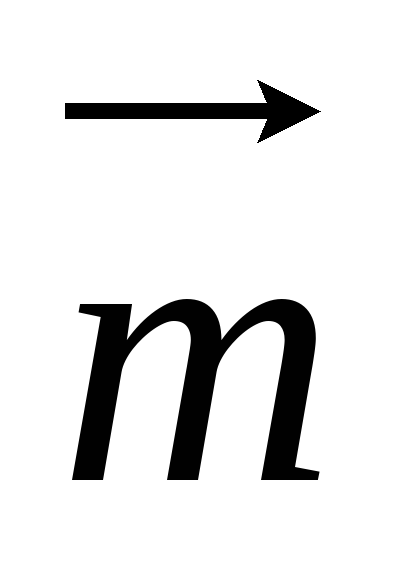 и
и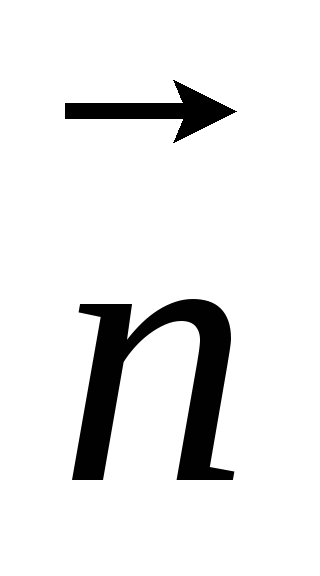 - единичные векторы и угол между ними
равен
- единичные векторы и угол между ними
равен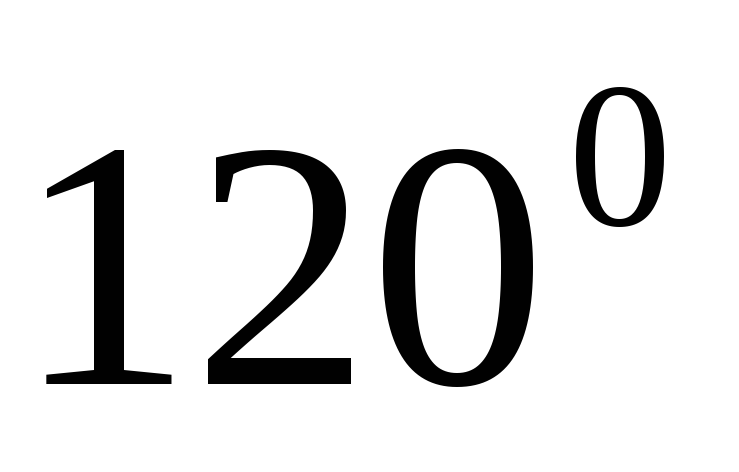 .
.
![]()
![]()
![]()
![]()
![]()
![]() .
.
7. Найти векторное
произведение векторов
![]() и
и![]()
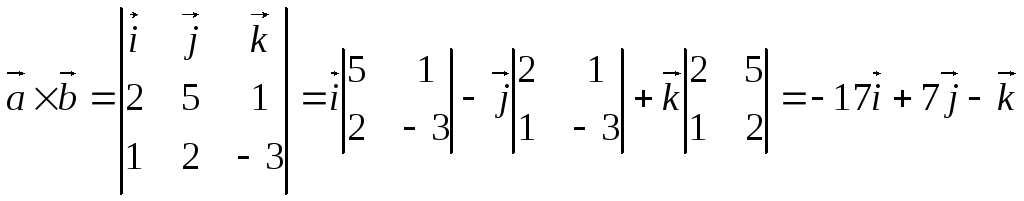 .
.
Вычислить площадь треугольника с вершинами
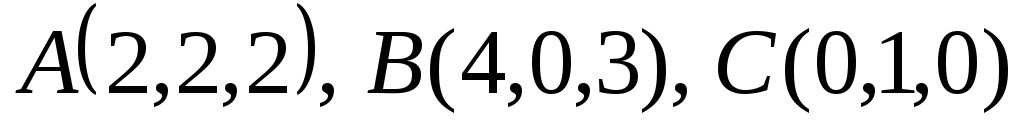 .
.
Решение:
![]()
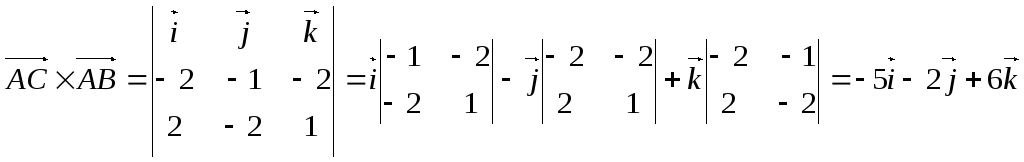
![]()
![]() .
.
Найти площадь параллелограмма, построенного на векторах
 и
и ,
если
,
если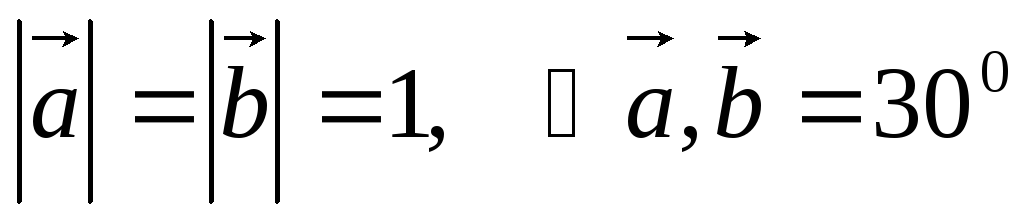 .
.
![]()
![]()
Даны точки
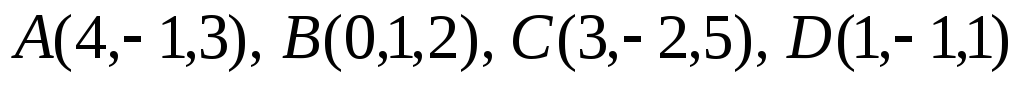 .
.
Найти: а). высоту
![]() ,
опущенную из вершиныА
на сторону ВС;
,
опущенную из вершиныА
на сторону ВС;
б). объём пирамиды ABCD.
а). С одной стороны
![]() ,
с другой стороны
,
с другой стороны![]() .
.
Таким образом,
![]() .
.
 B
B
![]()
h
A C

![]()
![]()
![]()
![]()
б). Объём пирамиды
ABCD
равен
![]() объёма параллелепипеда, построенного
на векторах
объёма параллелепипеда, построенного
на векторах![]() .
.
![]() .
.
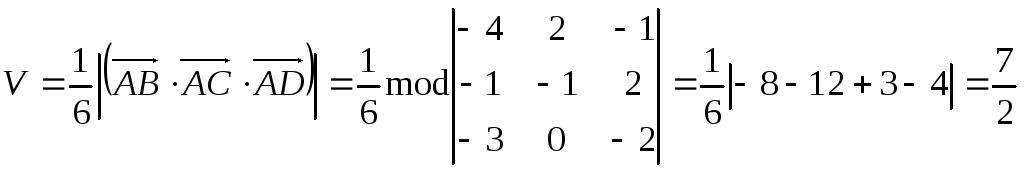 .
.
Доказать, что точки
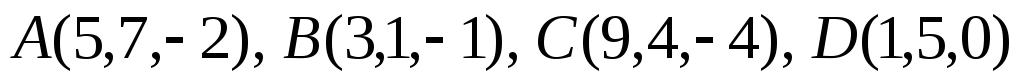 лежат в одной плоскости.
лежат в одной плоскости.
Рассмотрим векторы
![]() .
.
Найдём их смешанное произведение:
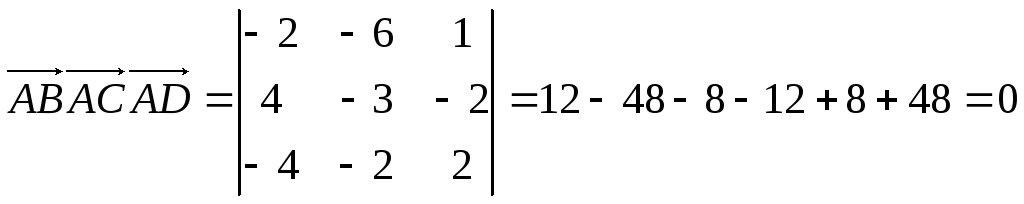
Значит, векторы компланарны, следовательно, точки A,B,C,D лежат в одной плоскости.
Дана пирамида, вершины которой имеют координаты:
 .
Найти высоту, опущенную на граньBCD.
.
Найти высоту, опущенную на граньBCD.
Решение:
С одной стороны
![]() с другой
с другой![]() .
.
Таким образом,
![]() .
.
Следовательно,
![]() .
.
![]() .
.
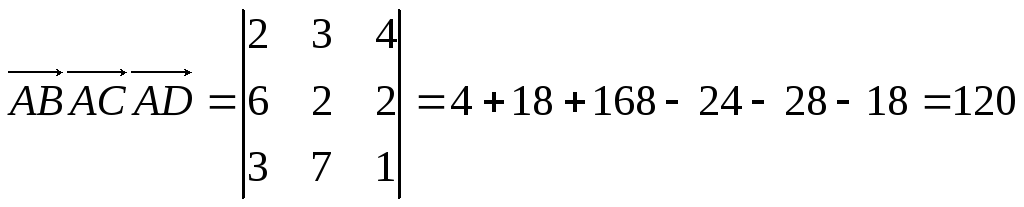
![]()
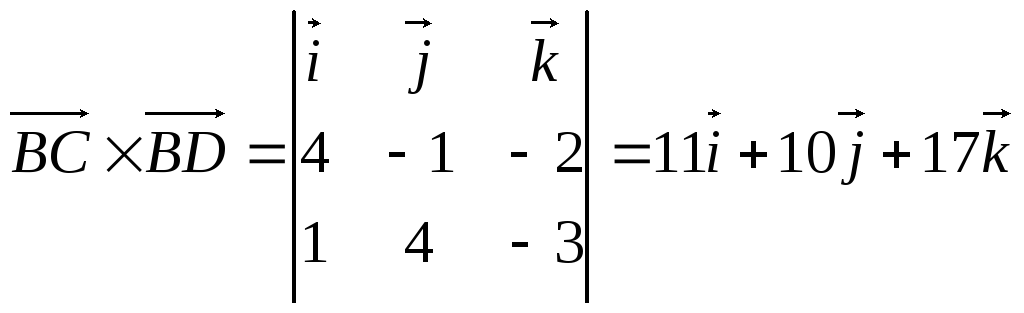
![]()
![]() .
.
