
- •Тверской государственный технический университет
- •Контрольная работа
- •Фамилия, имя, отчество
- •3. Обратная матрица
- •4. Ранг матрицы
- •5. Системы линейных уравнений
- •6. Примеры
- •Тема 2. Векторная алгебра и аналитическая геометрия
- •5. Прямая на плоскости.
- •6. Угол между двумя прямыми.
- •7. Плоскость в пространстве.
- •8. Прямая в пространстве.
- •Тема 3. Введение в математический анализ. Предел последовательности
- •Предел функции
- •Некоторые эталонные пределы
- •Непрерывность функции
- •Классификация точек разрыва
- •Производная и дифференциал
- •1) 2).
- •Правило Лопиталя
- •Часть 2
Часть 2
Вычислить пределы, не используя правило Лопиталя.
Задание 1
1)
![]() ;
6)
;
6)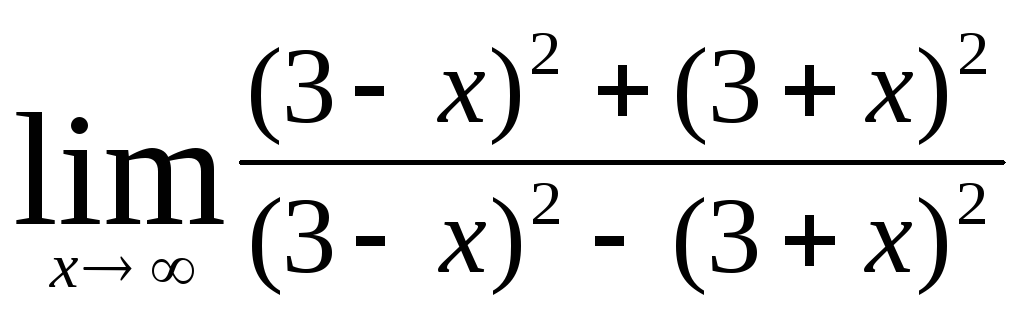 ;
;
2)
 ;
7)
;
7) ;
;
3)
![]() ;
8)
;
8)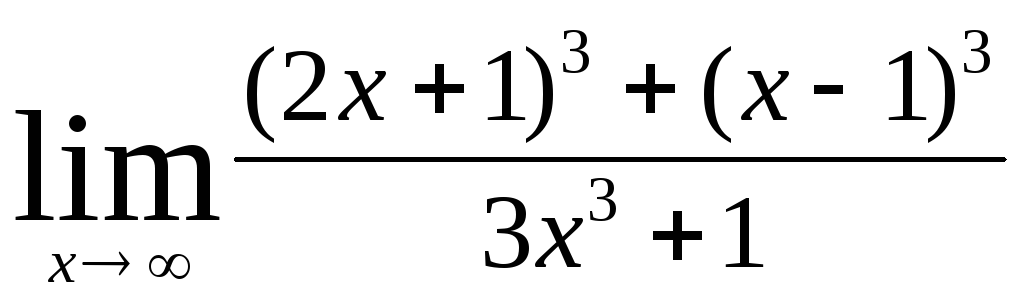 ;
;
4)
 ;
9)
;
9) ;
;
5)
 ;
10)
;
10) .
.
Задание 2
1)
![]() ;
6)
;
6)![]() ;
;
2)
![]() ;
7)
;
7) ;
;
3)
![]() ;
8)
;
8)![]() ;
;
4)
![]() ;
9)
;
9)![]() ;
;
5)
 ;
10)
;
10)![]() .
.
Задание 3
1)
 ;
6)
;
6)![]() ;
;
2)
![]() ;
7)
;
7)![]() ;
;
3)
 ;
8)
;
8)![]() ;
;
4)
![]() ;
9)
;
9) ;
;
5)
 ;
10)
;
10)![]() .
.
Задание 4
1)
![]() ;
6)
;
6)![]() ;
;
2)
![]() ;
7)
;
7)![]() ;
;
3)
![]() ;
8)
;
8)![]() ;
;
4)
![]() ;
9)
;
9)![]() ;
;
5)
![]() ;
10)
;
10)![]() .
.
Задание 5
1)
![]() ;
6)
;
6)![]() ;
;
2)
![]() ;
7)
;
7)![]() ;
;
3)
![]() ;
8)
;
8)![]() ;
;
4)
![]() ;
9)
;
9)![]() ;
;
5)
 ;
10)
;
10)![]() .
.
Вычислить производные:
Задание 6
1)
![]() ;
6)
;
6)![]() ;
2)
;
2)![]() ;
7)
;
7)![]() ;
;
3)
![]() ;
8)
;
8)![]() ;
;
4)
![]() ;
9)
;
9)![]() ;
;
5)
![]() ;
10)
;
10)![]() .
.
8)
![]() ;
10)
;
10)![]() .
.
Задание 7
1)
![]() ;
6)
;
6)![]() ;
;
2)
![]() ;
7)
;
7)![]() ;
;
3)
![]() ;
8)
;
8)![]() ;
;
4)
![]() ;
9)
;
9)![]() ;
;
5)
![]() ;
10)
;
10)![]() .
.
Задание 8
1)
![]() ;
6)
;
6)![]() ;
;
2)
![]() ;
7)
;
7)![]() ;
;
3)
![]() ;
8)
;
8)![]() ;
;
4)
![]() ;
9)
;
9)![]() ;
;
5)
![]() ;
10)
;
10)![]() .
.
Литература
Пискунов Н.С. Дифференциальное и интегральное исчисления, т.1
Шнейдер В.Е. и др. Краткий курс высшей математики, т.1
Минорский В.П. Сборник задач по высшей математике.
Данко П.Е. Высшая математика в упражнениях и задачах. Часть 1.
Рябушко А.П. Сборник индивидуальных заданий по высшей математике, т.1.
Запорожец Г.И. Руководство к решению задач по математическому анализу.
Программа к экзамену
Матрицы и определители (общие понятия). Прямоугольная, квадратная, единичная, транспонированная матрица. Свойства определителей. Алгебраические дополнения и миноры. Разложение определителя по строке (столбцу).
Операции над матрицами. Линейные операции, умножение матриц. Невырожденная, обратная матрица. Элементарные преобразования матрицы. Ранг матрицы. Нахождение обратной матрицы. Определение ранга.
Системы линейных уравнений. Однородная и неоднородная система линейных алгебраических уравнений. Совместная система. Теорема Кронекера-Капелли. Фундаментальная система решений, общее решение. Методы решения: правило Крамера, метод Гаусса.
Векторы (общие понятия). Определение вектора. Равенство, коллинеарность, компланарность векторов. Длина вектора. Проекция вектора на ось. Сложение векторов и умножение вектора на число. Линейные операции над векторами. Базис на плоскости и в пространстве. Линейная зависимость векторов. Разложение вектора по базису. Прямоугольные координаты и направляющие косинусы вектора
Умножение векторов. Скалярное, векторное и смешанное произведения векторов, их свойства, геометрический смысл, выражение через координаты сомножителей. Угол между векторами, условия их ортогональности, коллинеарности и компланарности.
Прямая линия. Уравнение прямой на плоскости, его различные формы. Расстояние от точки до прямой. Углы между прямыми, условия их параллельности, ортогональности.
Плоскость. Уравнения плоскости и прямой в пространстве. Расстояние от точки до плоскости. Углы между плоскостями, прямой и плоскостью, условия их параллельности, ортогональности.
Кривые второго порядка. Уравнения и свойства кривых второго порядка на плоскости:окружности, эллипса, гиперболы, параболы.
Предел функции одной переменной. Предел функции в точке. Свойства сходящихся функций. Односторонние пределы. Первый и второй замечательные пределы.
Непрерывность функции. Непрерывность в точке и на отрезке. Точки разрыва функции.
Производная функции. Приращение функции и аргумента. Геометрический и механический смысл производной (задачи о касательной и скорости). Дифференцируемость функции. Производные высших порядков.
Правила дифференцирования. Производная суммы, произведения и отношения функций. Дифференцирование сложной, параметрически заданной и обратной функций.
Раскрытие неопределенностей. Применение производных для нахождения пределов неопределенных выражений. Первое и второе правила Лопиталя.
Локальный экстремум, наибольшее и наименьшее значения функции. Необходимые и достаточные условия существования экстремума. Схема нахождения экстремумов, наибольшего и наименьшего значения функции.
Построение графика функции. Определение экстремумов, областей монотонности, выпуклости и вогнутости кривой, точек перегиба. Правило нахождения асимптот графика функции. Общая схема построения графика.
