
Задание 33
1. Составить уравнения касательной и нормали к линии у = х ln(2х — 1) в точке ее пересечения с осью ОХ.
2. В какой точке касательная к линии у = 2х2 + х + 3 параллельна прямой 5x + 2у — 1 = 0?
3. В какой точке касательная к линии у = 2х2 + 4х — 3 перпендикулярна прямой х + у — 1 = О?
4. Составить уравнения касательной и нормали к линии x2 - y2 + ху - 11 = 0 в точке М0(3; 2).
5.
Под каким углом пересекаются линии у
= 1/х и
у=![]() ?
?
6. Составить уравнения касательной и нормали к линии у = cos(x) + х в точке ее пересечения с осью ординат.
7. В какой точке касательная к линии у = x4 — 7 параллельна прямой у = 8х- 4?
8. В какой точке линии у = 7х2 — 5х + 4 касательная перпендикулярна прямой 32у + х - 1 = 0?
9. Составить уравнения касательной и нормали к линии x2/25 + у2/1б = 1 в точке М0(-4; 2, 4).
10. Составить уравнения касательной и нормали к линии у = 4 tg(3x) при х = π/9.
Задание 34
Найдите площадь треугольника, образованного прямой x=x0+1, касательной и нормалью, проведёнными к графику заданной функции в точке с заданной абсциссой x0 или в точке, соответствующей значению параметра t0.
1)
![]() ; 2)
; 2)
![]() ;
;
3)
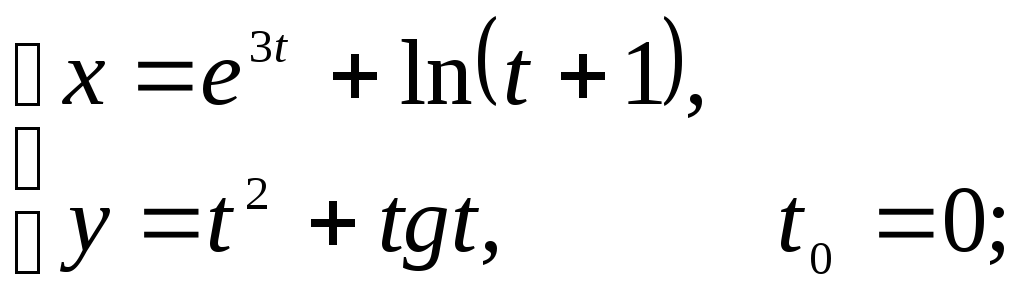 4)
4)
![]() ;
;
5)
![]() ; 6)
; 6)
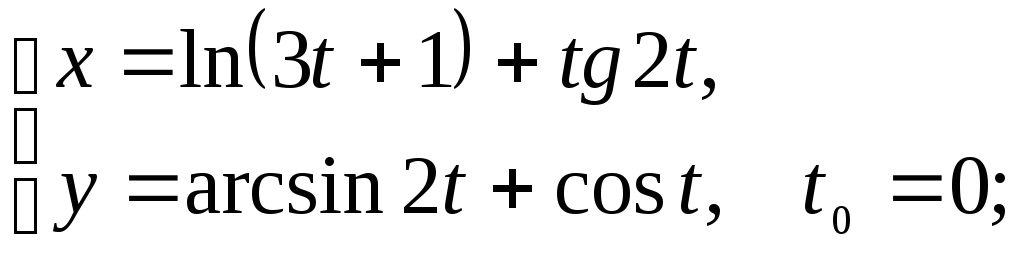
7)
![]() ; 8)
; 8)
![]() ;
;
9)
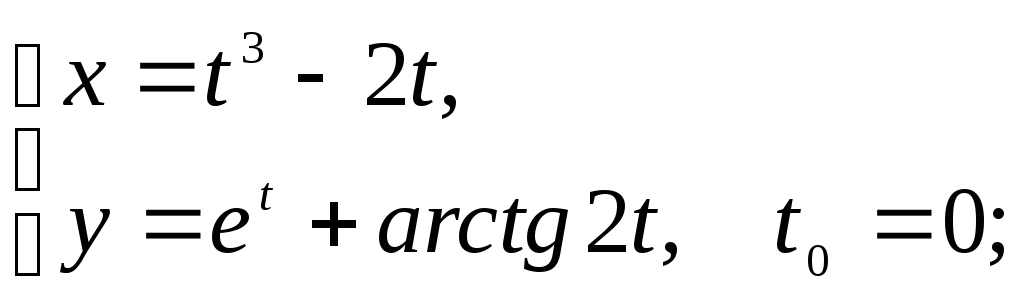 10)
10)
![]() .
.
ЗАДАНИЕ 35
Найдите пределы, используя правило Лопиталя:
|
1)
|
2)
|
3)
|
|
4)
|
5)
|
6)
|
|
7)
|
8)
|
9)
|
|
10)
|
|
|
ЗАДАНИЕ 36
Пользуясь правилом Лопиталя, найдите пределы:
1.
a)
![]() ;б)
;б)
![]() ;
;
2.
a)
![]() ;б)
;б)
![]() ;
;
3.
a)
![]() ;б)
;б)
![]() ;
;
4.
a)
![]() ;б)
;б)
![]() ;
;
5.
a)
![]() ;б)
;б)
![]() ;
;
6.
a)
![]() ;б)
;б)
![]() ;
;
7.
a)
![]() ;б)
;б)
![]() ;
;
8.
a)
![]() ;б)
;б)
![]() ;
;
9.
a)
![]() ;б)
;б)
![]() ;
;
10.
a)
![]() ;б)
;б)
![]() .
.
ЗАДАЧА 37
Найдите точки
экстремума функции
![]() .
.
1.
![]() ;
2.
;
2.![]() ;
;
3.
![]() ;
4.
;
4.![]() ;
;
5.
![]() ;
6.
;
6.![]() ;
;
7.
![]() ;
8.
;
8.![]() ;
;
9.
![]() ;
10.
;
10.![]() .
.
ЗАДАНИЕ 38
Найдите точки экстремума функции:
1)![]() 2)
2)![]()
3)
![]() 4)
4)![]()
5)
![]() 6)
6)![]()
7)
![]() 8)
8)![]()
9)
![]() 10)
10)![]()
ЗАДАНИЕ 39
Найдите наибольшее и наименьшее значение функции на отрезке:
1)![]() ;
2)
;
2)![]() ;
;
3)
![]() ;
4)
;
4)![]() ;
;
5)
![]() ;
6)
;
6)![]() ;
;
7)
![]() ;
8)
;
8)![]() ;
;
9)
![]() ;
10)
;
10)![]() .
.
ЗАДАНИЕ 40
Найти наименьшее и наибольшее значение функции на отрезке:
1)![]() ;
2)
;
2)![]() ;
;
3)
![]() ;
4)
;
4)![]() ;
;
5)
![]() ;
6)
;
6)![]() ;
;
7)
![]() ;
8)
;
8)![]() ;
;
9)
![]() ;
10)
;
10)![]() .
.
ЗАДАНИЕ 41
Для заданной функции f(x) = x4 + px3 + qx2 + rx +c и отрезка [a; b] (коэффициенты приведены в таблице) найдите: а) промежутки возрастания, убывания и точки экстремума; б) наибольшие и наименьшие значения функции на отрезке [a; b].
|
варианта |
p |
q |
r |
c |
a |
b |
|
1 |
12 |
52 |
96 |
-5 |
-5 |
0 |
|
2 |
-8/3 |
-2 |
8 |
3 |
0 |
3 |
|
3 |
16/3 |
2 |
-24 |
1 |
-4 |
0 |
|
4 |
8/3 |
-10 |
-24 |
2 |
-2 |
3 |
|
5 |
-16/3 |
12 |
0 |
-1 |
-2 |
2 |
|
6 |
8/3 |
2 |
-8 |
1 |
-3 |
1 |
|
7 |
32/3 |
-38 |
48 |
-3 |
-3 |
1 |
|
8 |
-4/3 |
-12 |
0 |
5 |
-3 |
1 |
|
9 |
4 |
-8 |
-48 |
1 |
-4 |
1 |
|
10 |
4/3 |
-18 |
-36 |
2 |
-2 |
4 |
Задание 42
Найдите точки перегиба кривой:
1)
![]() ;
2)
;
2)![]() ;
;
3)
![]() ;
4)
;
4)![]() ;
;
5)
![]() ;
6)
;
6)![]() ;
;
7)
![]() ;
8)
;
8)![]() ;
;
9)
![]() ;
10)
;
10)![]() .
.
ЗАДАНИЕ 43
Исследовать и построить графики функций:
a)
![]() ;
б)
;
б)
![]() .
.
Коэффициенты В, С приведены в таблице, n – номер варианта
(в задании б) точное нахождение точек перегиба не предполагается).
|
вар. |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
В |
2 |
3 |
4 |
1 |
2 |
3 |
4 |
5 |
7 |
-2 |
|
С |
3 |
4 |
5 |
6 |
8 |
10 |
12 |
16 |
18 |
3 |
