
Задание 20
Задана функция f(x). Найдите значения параметров, входящих в ее определение, при которых f(x) будет непрерывна и дифференцируема до 4 порядка включительно:
1)
|
f (x)
=
|
-5sin(a1 x+a2 x3) |
|
при x<0 ; |
|
-2x |
|
при
x |
2)
|
f (x)
=
|
(a1+a2 cos(x)) sin(x) |
|
при x<0 ; |
|
-3(x-x3) |
|
при
x |
3)
|
f (x)
=
|
2arctg(x) |
|
при x<0 ; |
|
(a1+a2 cos(x)) sin(x) |
|
при
x |
4)
|
f (x)
=
|
(a1+a2 cos(x)) sin(x) |
|
при x<0 ; |
|
-2arcsin(x) |
|
при
x |
5
|
(x)
=
|
-4arctg(x) |
|
при x<0 ; |
|
(a1+a2 cos(x)) sin(x) |
|
при
x |
6
|
f (x)
=
|
5sin(a1 x+a2 x3) |
|
при x<0 ; |
|
5x |
|
при
x |
7
|
f (x)
=
|
a1 sqrt(1+a2 x2) |
|
при x<0 ; |
|
-3+9sin(x2) |
|
при
x |
8
|
f (x)
=
|
4tg(a1 x+a2 x3) |
|
при x<0 ; |
|
3x |
|
при
x |
9
|
f (x)
=
|
4x |
|
при x<0 ; |
|
-4tg(a1 x+a2 x3) |
|
при
x |
10
|
f (x)
=
|
(a1+a2 cos(x)) sin(x) |
|
при x<0 ; |
|
-5(x-x3) |
|
при
x |
Задание 21
Дана функция
![]() .
В какой точке обратная функция не имеет
производной?
.
В какой точке обратная функция не имеет
производной?
1.
![]() ;2.
;2.
![]() ;
;
3.
![]() ;4.
;4.
![]() ;
;
5.
![]() ;6.
;6.
![]() ;
;
7.
![]() ;8.
;8.
![]() ;
;
9.
![]() ;10.
;10.
![]() .
.
ЗАДАНИЕ 22
Функция
![]() монотонна на указанном промежутке.
Найдите производную обратной функции
монотонна на указанном промежутке.
Найдите производную обратной функции![]() .
.
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
ЗАДАНИЕ 23
Найдите производные первого и второго порядков в точке M(x0, y0) от функции, заданной неявно:
1)
![]() ,
M(1;
1) ; 2)
,
M(1;
1) ; 2)
![]() ,
M(1;
-/4)
;
,
M(1;
-/4)
;
3)
![]() ,
M(1;
-1) ; 4)
,
M(1;
-1) ; 4)
![]() ,
M(0;
/4)
;
,
M(0;
/4)
;
5)
![]() ,
M(1;
1) ; 6)
,
M(1;
1) ; 6)
![]() ,
M(0;
/4)
;
,
M(0;
/4)
;
7)
![]() ,
M(0;
1) ; 8)
,
M(0;
1) ; 8)
![]() ,
M(1;
0) ;
,
M(1;
0) ;
9)
![]() ,
M(0;
1) ; 10)
,
M(0;
1) ; 10)
![]() ,
M(1;
1) .
,
M(1;
1) .
ЗАДАНИЕ 24
Найдите производные 1-го и 2-го порядков от функций, заданных параметрически:
1)
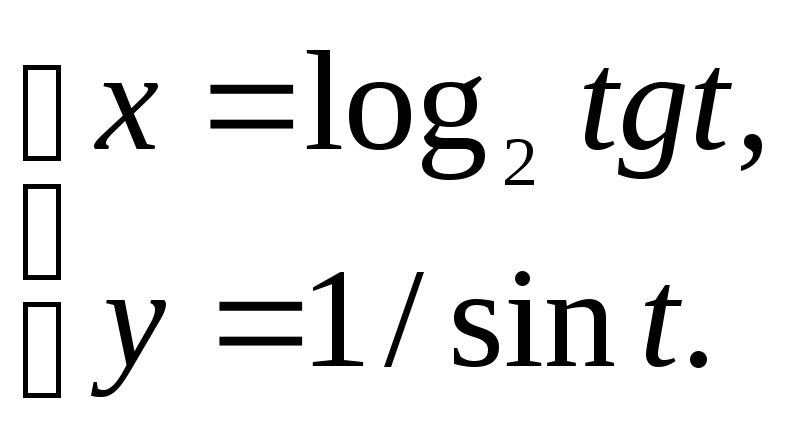 2)
2)
 3)
3)

4)
 5)
5)

6)
 7)
7)
 8)
8)

9)
 10)
10)

ЗАДАНИЕ 25
Найти производные от функций:
1) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ;
;
г)
![]() д)
д)![]() ; е)
; е)![]()
2) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ;
;
г)
![]() д)
д)![]() ; е)
; е)![]()
3) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ;
;
г)
![]() д)
д)![]() ; е)
; е)![]()
4) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ;
;
г)
![]() д)
д)![]() ; е)
; е)![]()
5) а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
;
г)
![]() д)
д)![]() ; е)
; е)
6) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ;
;
г)
![]() д)
д)![]() ; е)
; е)![]()
7) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ;
;
г)
![]() д)
д)![]() ; е)
; е)
8) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ;
;
г)
![]() д)
д)![]() ; е)
; е)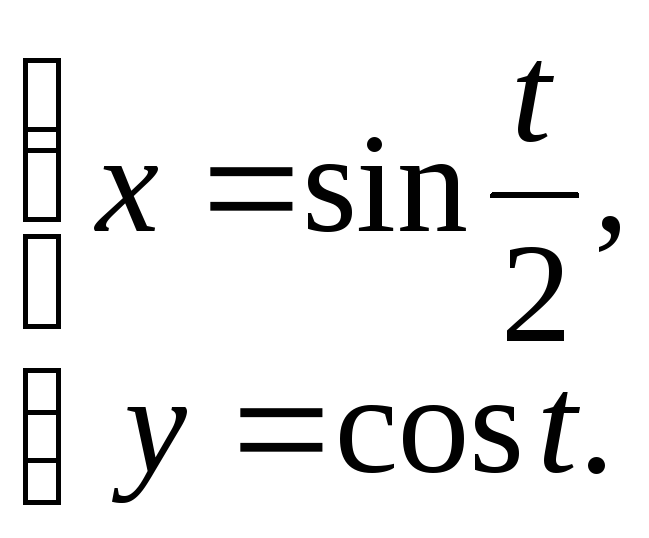
9) а)
![]() ; б)
; б)![]() ;
в)
;
в)![]() ;
;
г)
![]() д)
д)![]() ; е)
; е)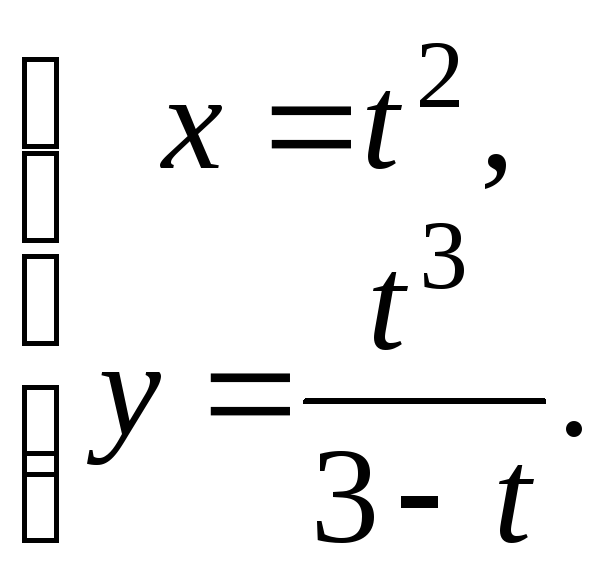
10) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ;
;
г)
![]() д)
д)![]() ; е)
; е)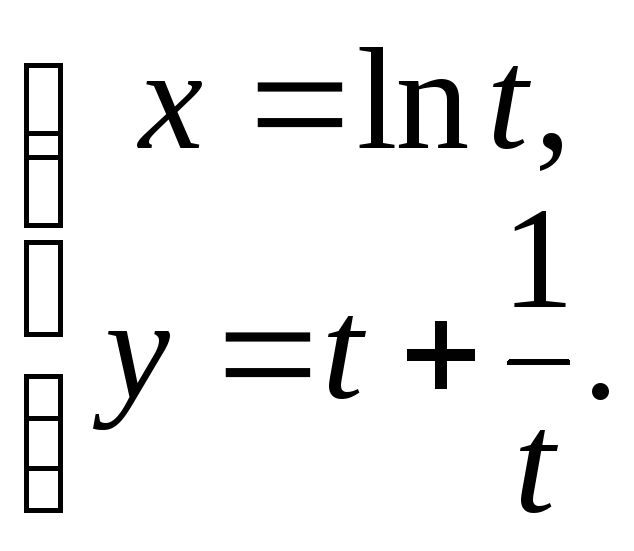
ЗАДАНИЕ 26
Найдите вторые производные от функций:
1)
а)![]() ;
б)
;
б)
2)
а)![]() б)
б)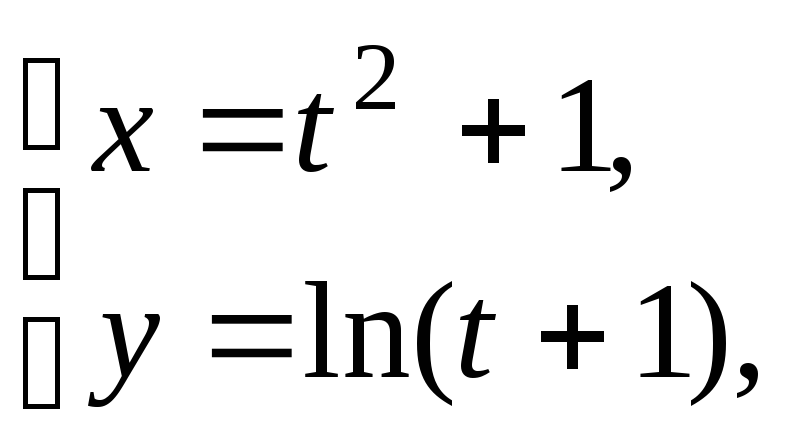
3)
а)![]() б)
б)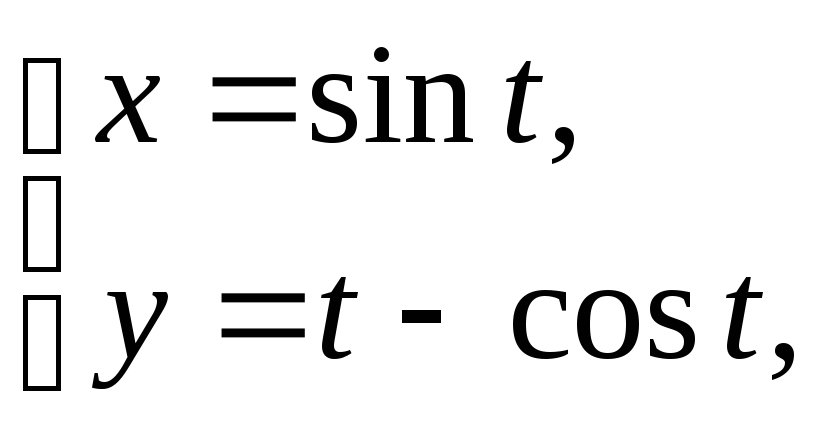
4)
а)![]() б)
б)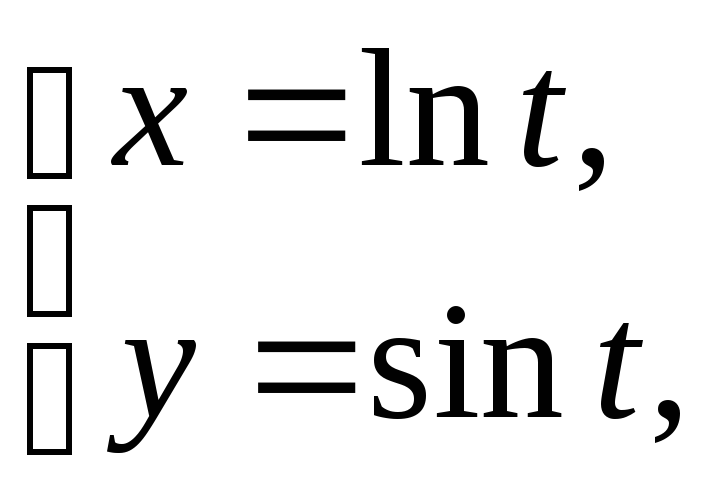
5)
а)![]() б)
б)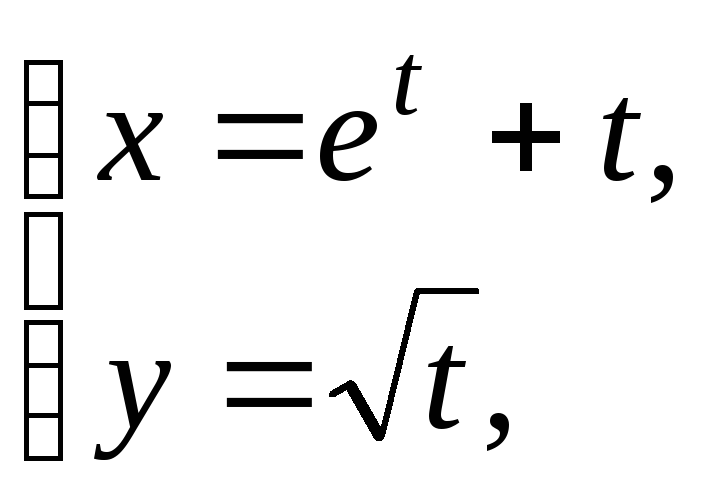
6) а)![]() ;
б)
;
б)
7)
а)![]() б)
б)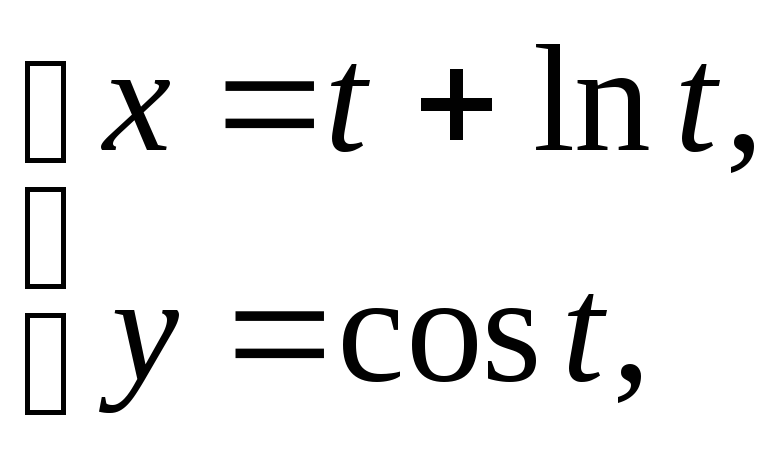
8)
а)![]() б)
б)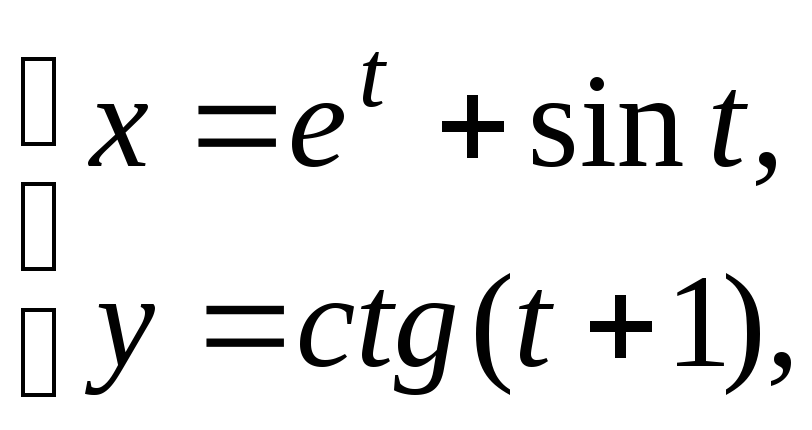
9)
а)![]() б)
б)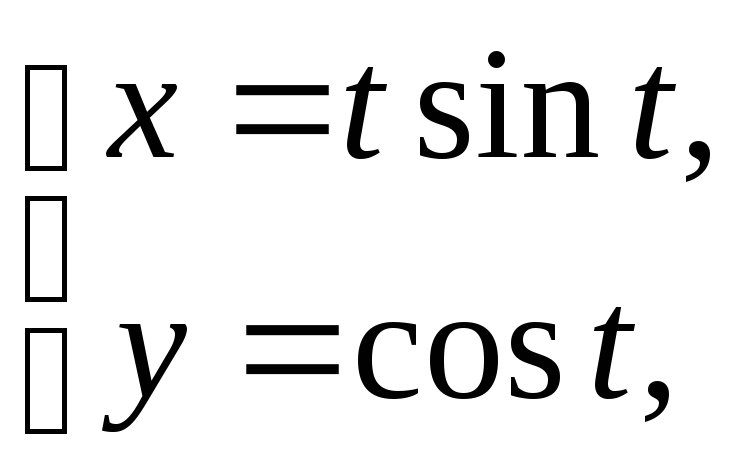
10) а)![]() б)
б)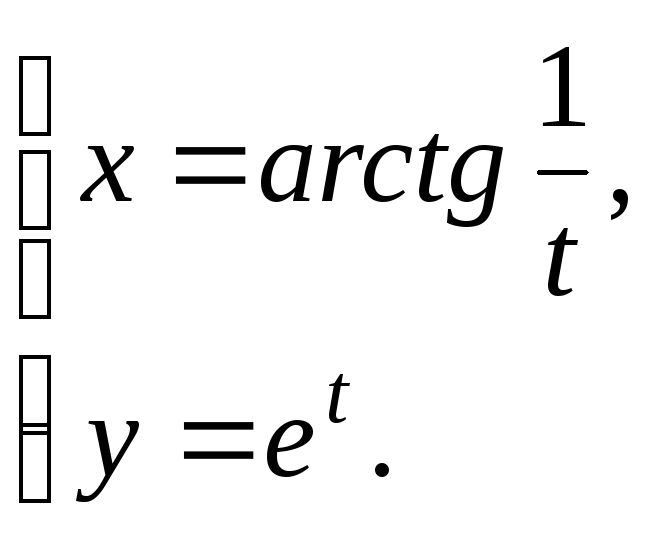
ЗАДАНИЕ 27
Найти дифференциалы указанных порядков от данных функций.
1)
![]() ,
,![]() ;2)
;2)
![]() ,
,![]() ;3)
;3)
![]() ,
,![]() ;
;
4)
![]() ,
,![]() ;5)
;5)
![]() ,
,![]() ;6)
;6)
![]() ,
,![]() ;
;
7)
![]() ,
,![]() ;8)
;8)
![]() ,
,![]() ;9)
;9)
![]() ,
,![]() ;
;
10)
![]() ,
,![]() .
.
ЗАДАНИЕ 28
Найдите сумму
коэффициентов
![]() и
и![]() уравнения касательной
уравнения касательной![]() ,
проведенной к кривой
,
проведенной к кривой![]() в точке
в точке![]() .
.
1.
![]() ;
2.
;
2.
![]() ;
;
3.
![]() ;
4.
;
4.
![]() ;
;
5.
![]() ;
6.
;
6.
![]() ;
;
7.
![]() ;
8.
;
8.
![]() ;
;
9.
![]() ;
10.
;
10.
![]() .
.
ЗАДАНИЕ 29
Составьте уравнения
касательной и нормали к кривой в точке
![]() :
:
1)![]() ;
2)
;
2)![]() ;
;
3)
![]() ;
4)
;
4)![]() ;
;
5)
![]() ;
6)
;
6)![]() ;
;
7)
![]() ;
8)
;
8)![]() ;
;
9)
![]() ;
10)
;
10)![]() .
.
ЗАДАНИЕ 30
Найдите угол между кривыми:
|
№ |
|
|
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
ЗАДАНИЕ 31
Составьте уравнение
касательных к графику функции
![]() в точках
пересечения с осью ОХ
(в задачах
1-5) и с осью
ОY
( в задачах
6-10).
в точках
пересечения с осью ОХ
(в задачах
1-5) и с осью
ОY
( в задачах
6-10).
|
1)
|
6)
|
|
2)
|
7)
|
|
3)
|
8)
|
|
4)
|
9)
|
|
5)
|
10)
|
ЗАДАНИЕ 32
1.
Найти угол наклона к оси абсцисс
касательной к гиперболе
![]() в точке А(1;1).
в точке А(1;1).
2.
В какой точке кривой
![]() касательная перпендикулярна к прямой
касательная перпендикулярна к прямой![]() ?
?
3.
Найти точку на кривой
![]() ,
касательная в которой перпендикулярна
к прямой
,
касательная в которой перпендикулярна
к прямой![]() ?
?
4.
Найти точку на кривой
![]() ,
касательная в которой параллельна
прямой
,
касательная в которой параллельна
прямой![]() ?
?
5.
Найти расстояние от вершины параболы
![]() ,
до касательной к ней в точке пересечения
параболы с осью ординат.
,
до касательной к ней в точке пересечения
параболы с осью ординат.
6.
Написать уравнение касательной к кривой
![]() ,
если эта касательная проходит через
начало координат.
,
если эта касательная проходит через
начало координат.
7.
Написать уравнение нормали к кривой
![]() в точке с абсциссой
в точке с абсциссой![]() .
.
8.
В какой точка кривой
![]() касательная составляет с осью абсцисс
угол
касательная составляет с осью абсцисс
угол![]() ?
?
9. Определить
угловой коэффициент касательной к
кривой
![]() в
точке (3;2).
в
точке (3;2).
10.
Составить уравнения касательных,
проведенных из точки М(1;-3) к параболе
![]() .
.
