
Формул правильные?
-
1.
(1/g(x))' = 1/g'(x)
2 .
(1/g(x))' = -g'(x)/g(x)2
3.
(g(f(x)))' = g'(f(x)) f'(x)
4 .
(g(x) f(x))' = g(x) f'(x) + g'(x) f(x)
10.
Пусть
![]() и
и![]() две дифференцируемые функции. Какие из
приведенных
две дифференцируемые функции. Какие из
приведенных
Формул не правильные?
|
1. |
|
(f(g(x)))' = f'(g(x)) g'(x) |
|
2 . |
|
(f(x)/g(x))' = (f'(x) g(x) - f(x) g'(x))/g(x)2 |
|
3 . |
|
(f(x)/g(x))' = (f'(x) g(x) + f(x) g'(x))/g(x)2 |
|
4. |
|
(1/f(x))' = -f'(x)/f(x)2 |
ЗАДАНИЕ 7
Используя таблицу производных и правила дифференцирования, найдите производные следующих функций:
1)
![]() ;2)
;2)
![]() ;3)
;3)
![]() ;
;
4)
![]() ; 5)
; 5)
![]() ; 6)
; 6)
![]() ;
;
7)
![]() ; 8)
; 8)
![]() ; 9)
; 9)
![]() ;
;
10)
![]() .
.
ЗАДАНИЕ 8
Найдите производную первого порядка от функции:
1)
![]() ; 2)
; 2)
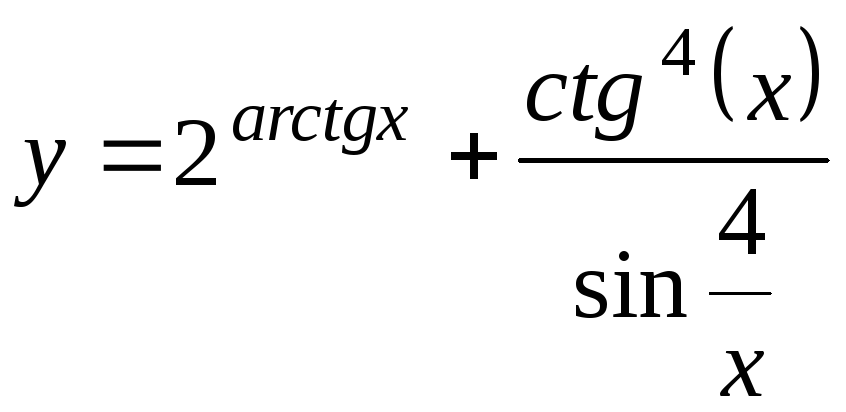 ;
;
3)
![]() ; 4)
; 4)
![]() ;
;
5)
![]() ; 6)
; 6)
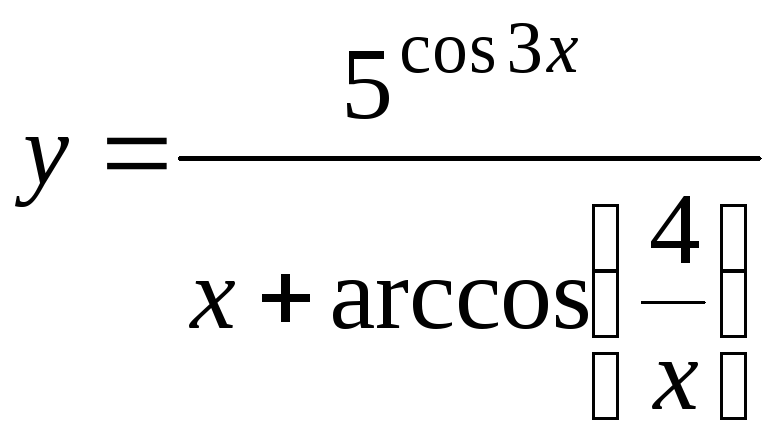 ;
;
7)
![]() ; 8)
; 8)
![]() ;
;
9)
![]() ;
10)
;
10)
![]() .
.
ЗАДАНИЕ 9
Найдите производную первого порядка от функции:
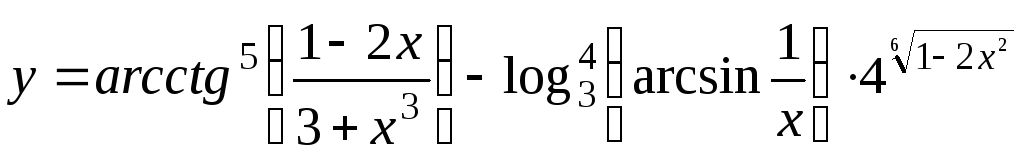 ;
;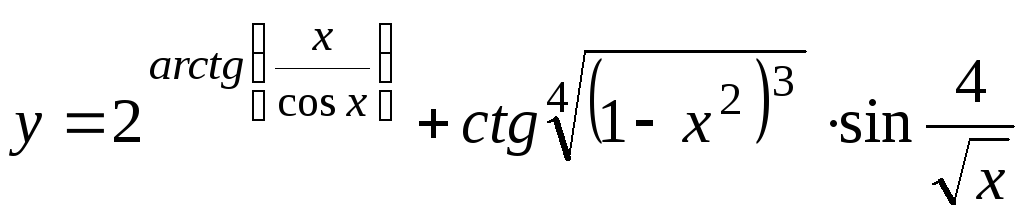 ;
; ;
;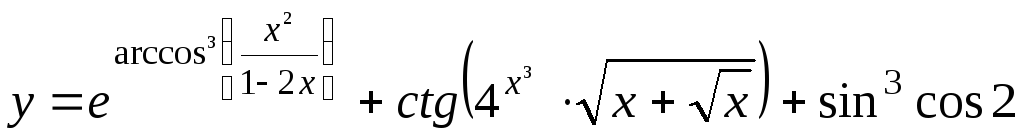 ;
;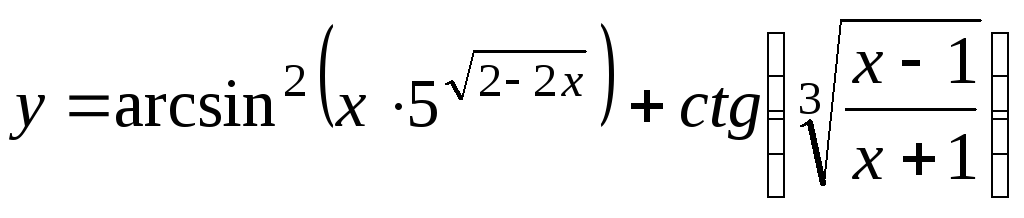 ;
;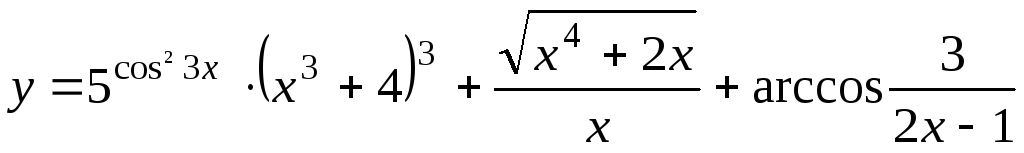 ;
;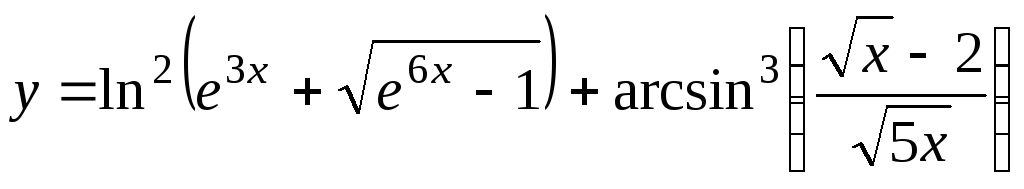 ;
;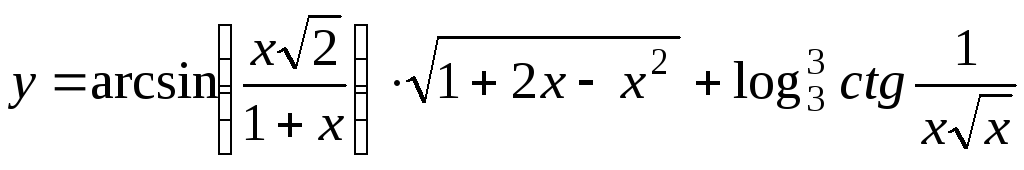 ;
;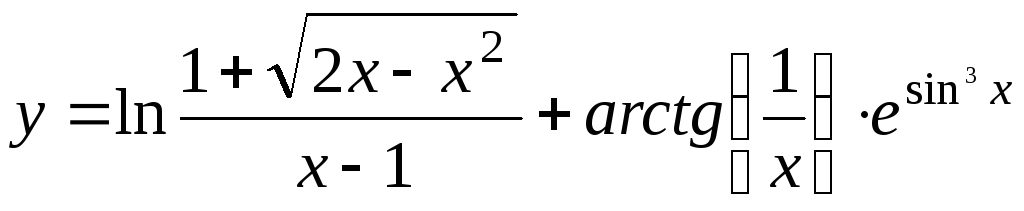 ;
;
10.
![]() .
.
ЗАДАНИЕ 10
Найдите
дифференциал
![]() :
:
1)
![]() 2)
2)
![]() ;
;
3)
![]() ;
4)
;
4)![]() ;
;
5)
![]() ;
6)
;
6)![]() ;
;
7)
![]() ;
8)
;
8)
![]() ;
;
9)
![]() ;
10)
;
10)![]() .
.
ЗАДАНИЕ 11
Найдите
производную
![]() :
:
1)
![]() ; 2)
; 2)![]() ;
;
3)
![]() ; 4)
; 4)![]() ;
;
5)
![]() ; 6)
; 6)![]() ;
;![]()
7)
![]() ; 8)
; 8)![]() ;
;
9)
![]() ; 10)
; 10)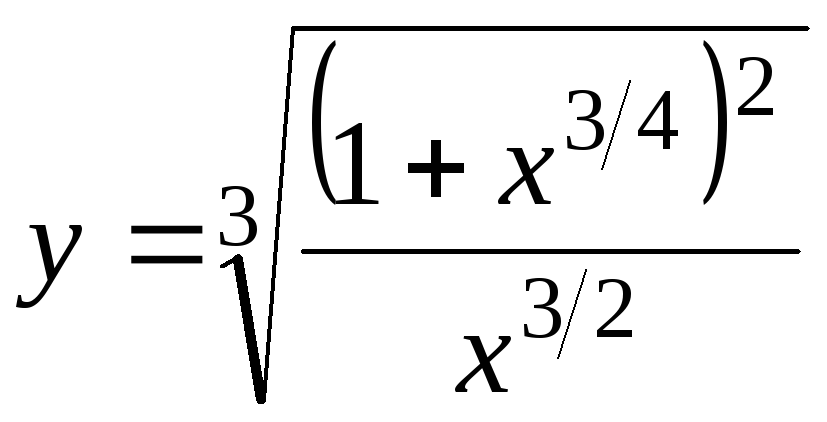 .
.
ЗАДАНИЕ12
Найти
производную
![]() :
:
1)
![]()
![]() ;
2)
;
2)![]() ;
;
3)
![]() ;
4)
;
4)![]() ;
;
5)
![]() ;
6)
;
6)![]() ;
;
7)
![]() ;
8)
;
8)![]() ;
;
9)
![]() ;
;
10)
![]() .
.
ЗАДАНИЕ 13
Найдите
производную
![]() :
:
1)
![]() ; 2)
; 2)
![]() ;
;
3)
![]() ; 4)
; 4)![]() ;
;
5)
![]() ; 6)
; 6)![]() ;
;
7)
![]() ; 8)
; 8)![]() ;
;
9)
![]() ; 10)
; 10)![]() .
.
ЗАДАНИЕ 14
Применяя метод логарифмического дифференцирования, найдите производные функций:
1)
a)
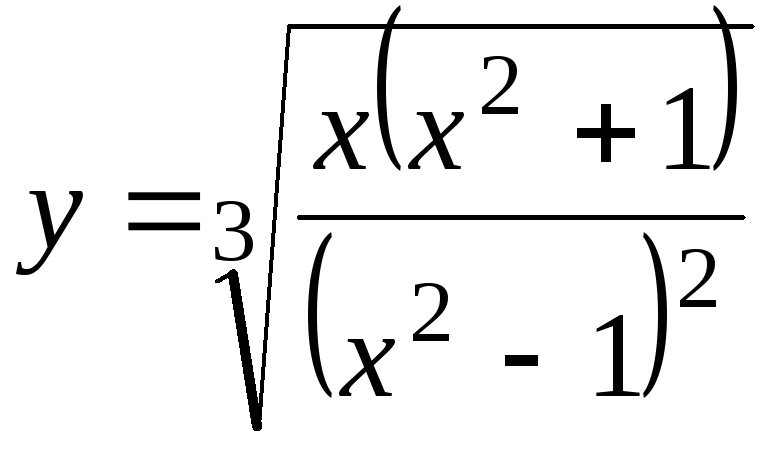 ;б)
;б)
![]() ;
;
2)
a)
![]() ;б)
;б)
![]() ;
;
3)
a)
![]() ;б)
;б)
![]() ;
;
4)
a)
![]() ;б)
;б)
![]() ;
;
5)
a)
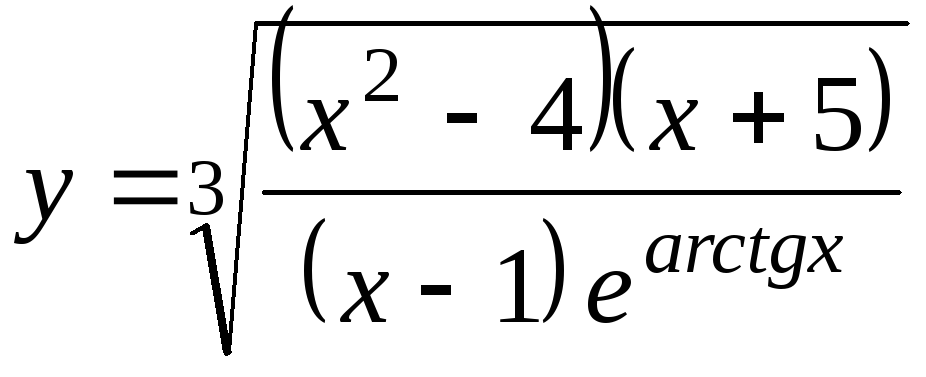 ;б)
;б)
![]() ;
;
6)
a)
![]() ;б)
;б)
![]() ;
;
7)
a)
![]() ;б)
;б)
![]() ;
;
8)
a)
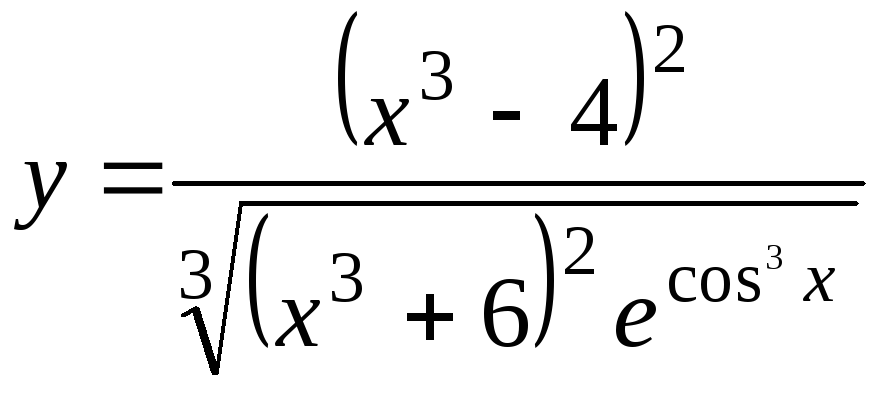 ;б)
;б)
![]() ;
;
9)
a)
![]() ;б)
;б)
![]() ;
;
10)
a)
![]() ;б)
;б)
![]() .
.
ЗАДАНИЕ 15
Проверьте, что данная функция удовлетворяет дифференциальному уравнению:
1)
![]() ,
, ![]() ;
;
2)
![]() ,
, ![]() ;
;
3)
![]() ,
, ![]() ;
;
4)
![]() ,
, ![]() ;
;
5)
![]() ,
, ![]() ;
;
6)
![]() ,
, ![]() ;
;
7)
![]() ,
, ![]() ;
;
8)
![]() ,
, ![]() ;
;
9)
![]() ,
, ![]() .
.
ЗАДАНИЕ 16
Найдите
![]() ,
,![]() :
:
1)
![]() ; 2)
; 2)
![]() ; 3)
; 3)
![]() ;
;
4)
![]() ; 5)
; 5)
![]() ; 6)
; 6)
![]() ;
;
7)
![]() ; 8)
; 8)
![]() ; 9)
; 9)
![]() ;
;
10)
![]() .
.
ЗАДАНИЕ 17
Найдите производную n-го порядка:
1)
![]()
![]() ; 2)
; 2)![]() ;
;
3)
![]() ; 4)
; 4)![]() ;
;
5)
![]() ; 6)
; 6)![]() ;
;
7)
![]() ; 8)
; 8)![]() ;
;
9)
![]() ; 10)
; 10)![]() .
.
ЗАДАНИЕ 18
Найдите производную указанного порядка:
1)
![]() ; 2)
; 2)![]() ;
;
3)
![]() ; 4)
; 4)![]() ;
;
5)
![]() ; 6)
; 6)![]() ;
;
7)
![]() ; 8)
; 8)![]() ;
;
9)
![]() ; 10)
; 10)![]() .
.
ЗАДАНИЕ 19
Задана функция f(x). Найдите значения параметров, входящих в ее определение, при которых f(x) будет непрерывна и дифференцируема до 2 порядка включительно:
1.
|
f (x)
=
|
a3 x2+3x-1 |
|
при x<0 ; |
|
a1 exp(a2 x) |
|
при
x |
2
|
f (x)
=
|
a1 exp(a2 x) |
|
при x<0 ; |
|
a3 x2+2x-1 |
|
при
x |
3
|
f (x)
=
|
a1 exp(a2 x) |
|
при x<0 ; |
|
a3 x2+2x-4 |
|
при
x |
4
|
f (x)
=
|
-5+2cos(x) |
|
при x<0 ; |
|
a1 x2+a2 x+a3 |
|
при
x |
5
|
f (x)
=
|
2-4ln(1+x) |
|
при x<0 ; |
|
a1 x2+a2 x+a3 |
|
при
x |
6
|
f (x)
=
|
-2cos(x)-2sin(x) |
|
при x<0 ; |
|
a1+a2 x+a3 x2 |
|
при
x |
7
|
f (x)
=
|
a1 cos(x)+a2 sin(x) |
|
при x<0 ; |
|
a3 x2-3x+4 |
|
при
x |
8
|
f (x)
=
|
a3 x2-3x-5 |
|
при x<0 ; |
|
a1 cos(x)+a2 sin(x) |
|
при
x |
9
|
f (x)
=
|
a1 x2+a2 x+a3 |
|
при x<0 ; |
|
-4-2ln(1+x) |
|
при
x |
10
|
f (x)
=
|
a1+a2 x+a3 x2 |
|
при x<0 ; |
|
3exp(4x) |
|
при
x |
