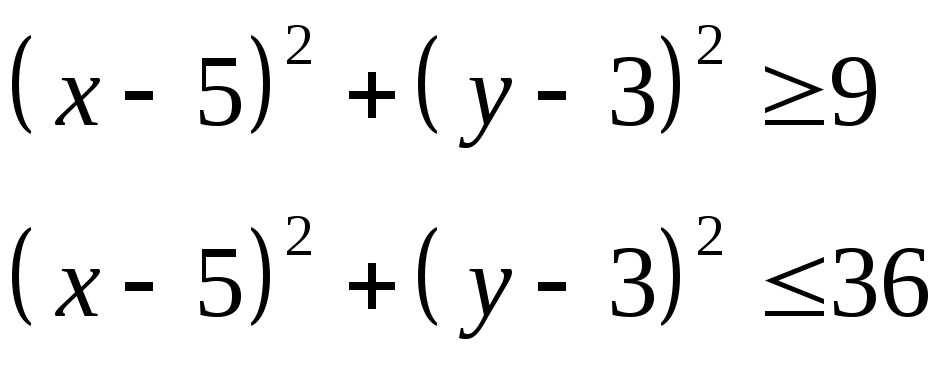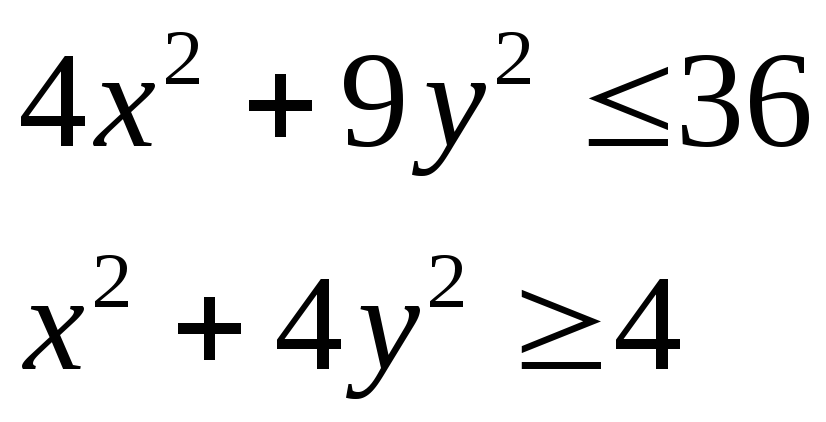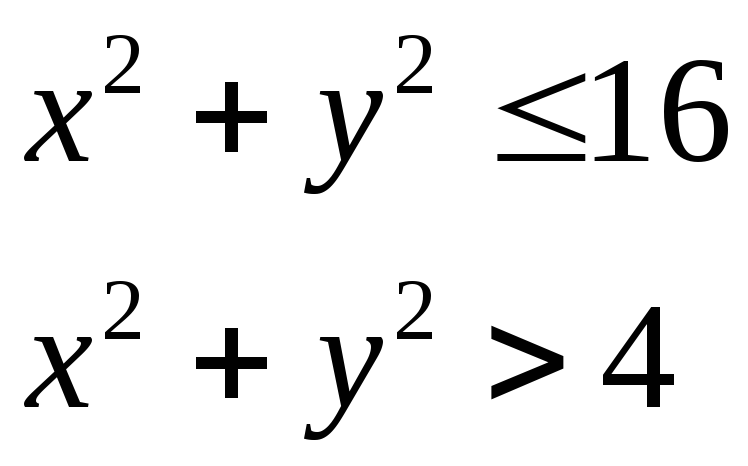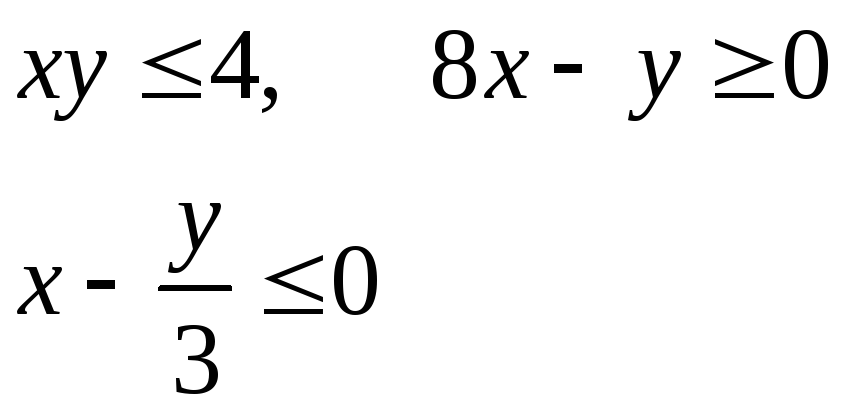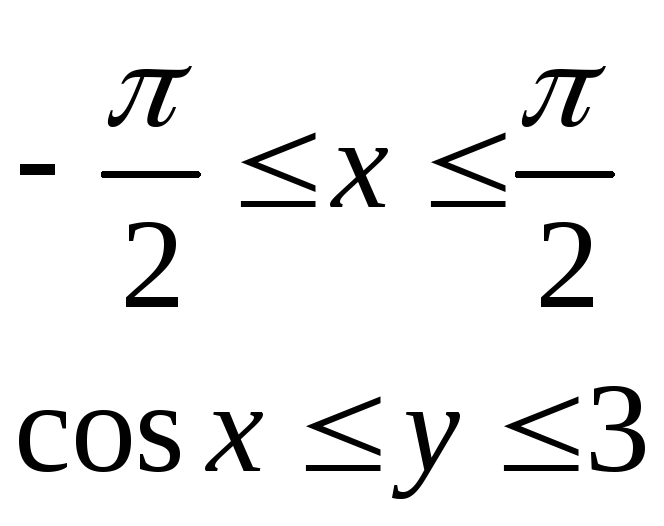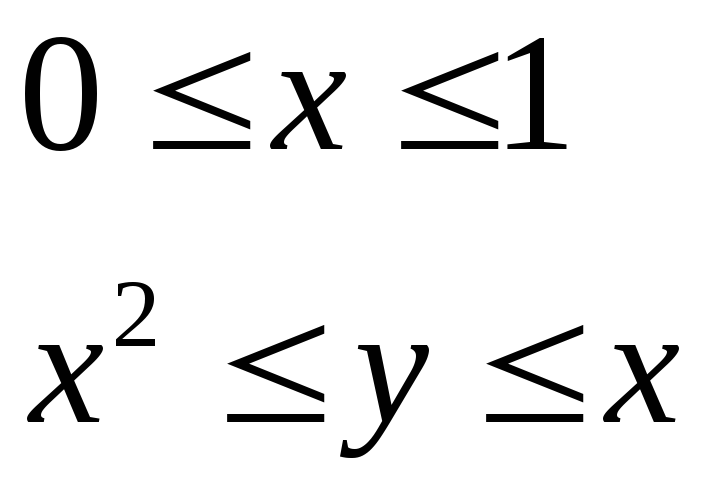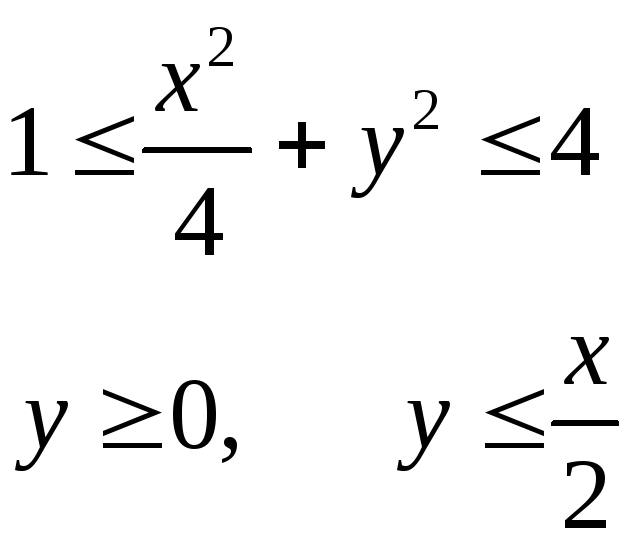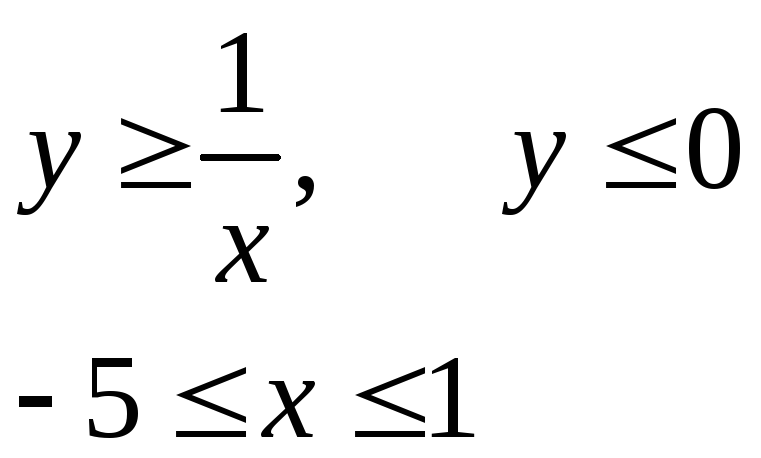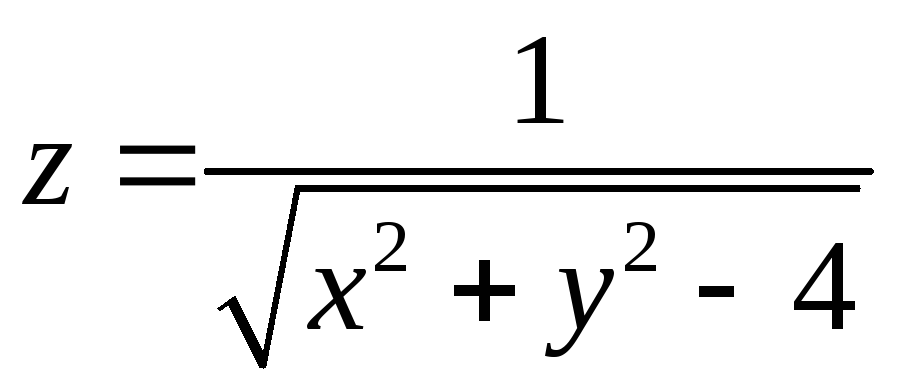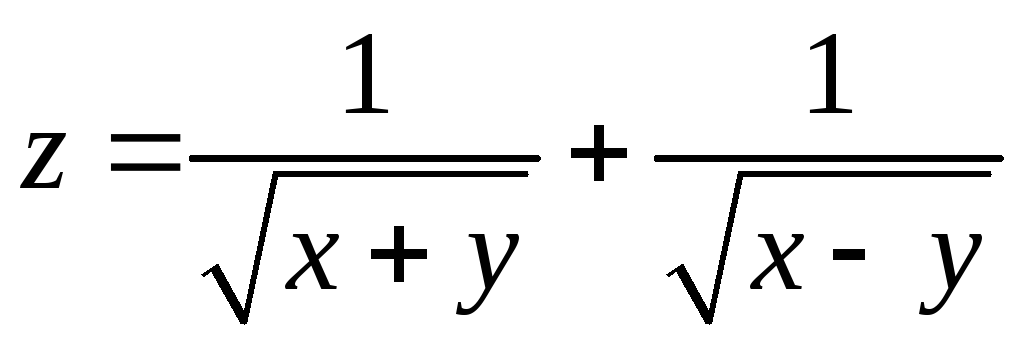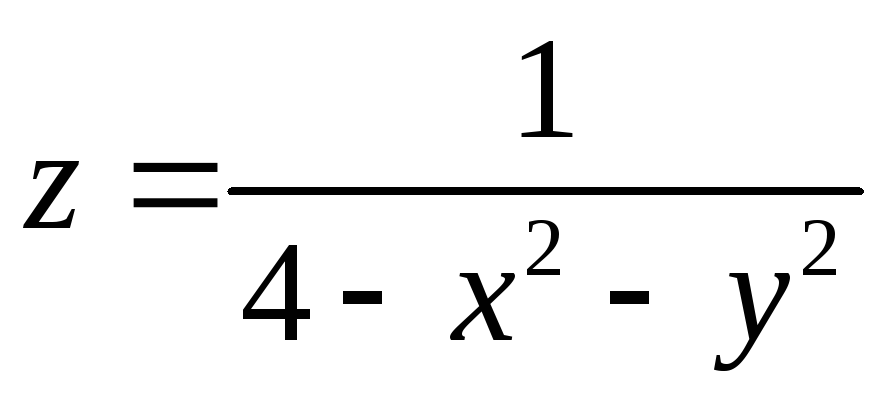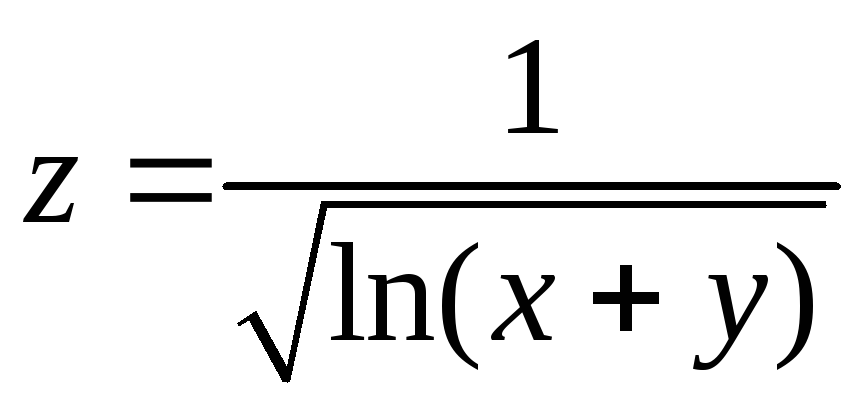Глава 5
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ
НЕСКОЛЬКИХ ПЕРЕМЕННЫХ И ЕГО ПРИЛОЖЕНИЯ
ЗАДАНИЕ 1
Изобразить область, заданную неравенствами:
|
Вариант
|
Область
|
Вариант |
Область |
|
1
|
|
2 |
|
|
3
|
|
4 |
|
|
5 |
|
6 |
|
|
7 |
|
8 |
|
|
9 |
|
10 |
|
ЗАДАНИЕ 2
Найдите область определения функции
|
Вариант |
Функция |
Вариант
|
Функция |
|
1
|
|
2 |
|
|
3
|
|
4 |
|
|
5
|
|
6 |
|
|
7
|
|
8 |
|
|
9
|
|
10 |
|
ЗАДАНИЕ 3
Найдите пределы
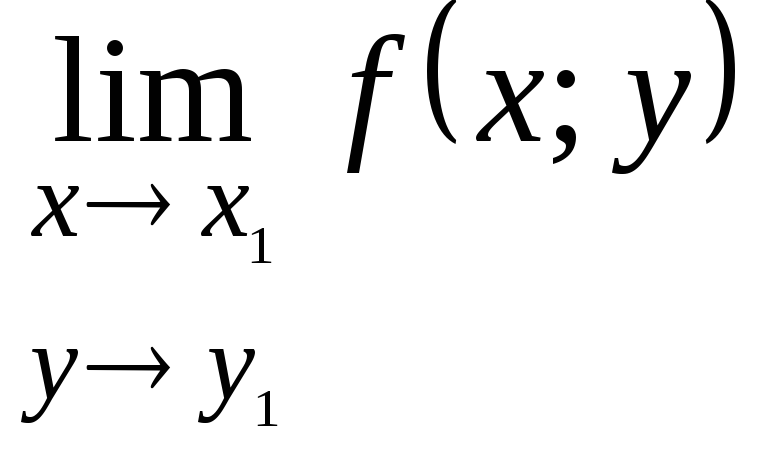 и
и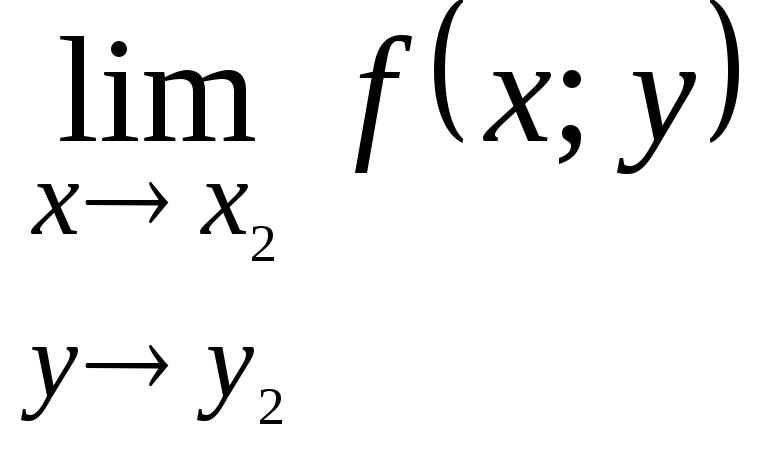 .
.
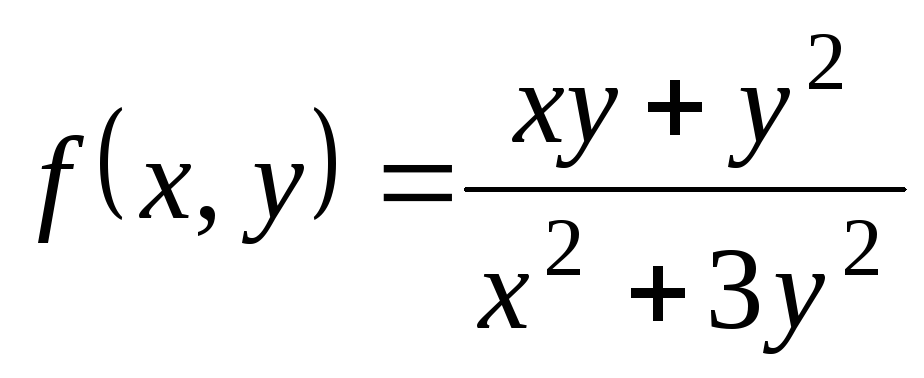 ,
, 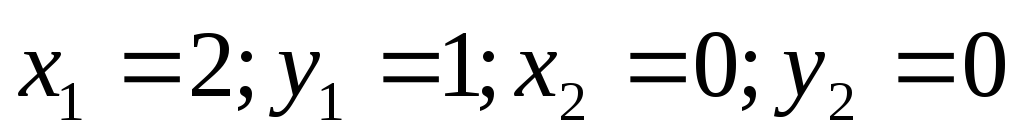 ;
;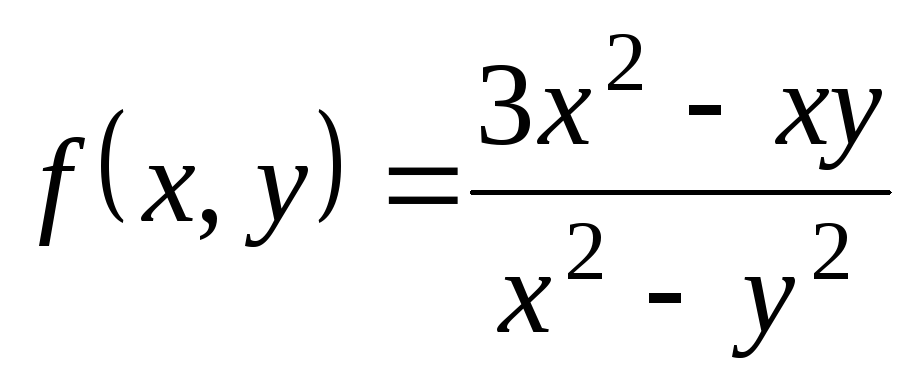 ,
, 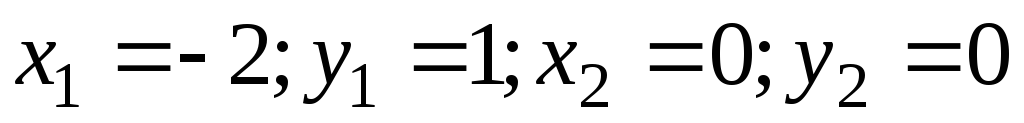 ;
;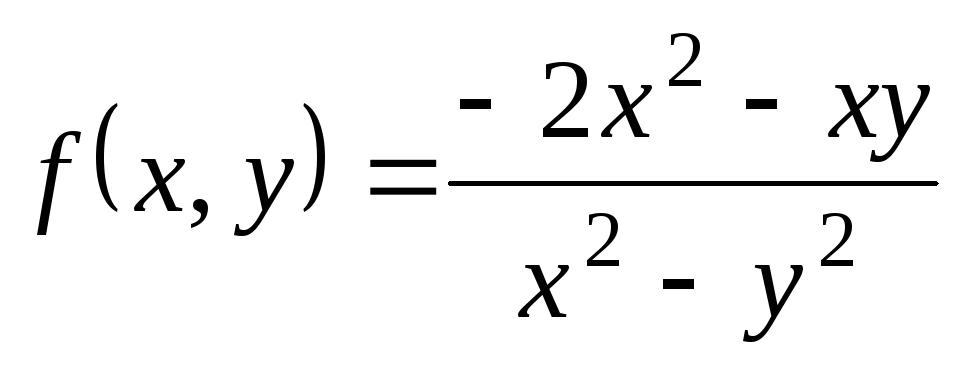 ,
,
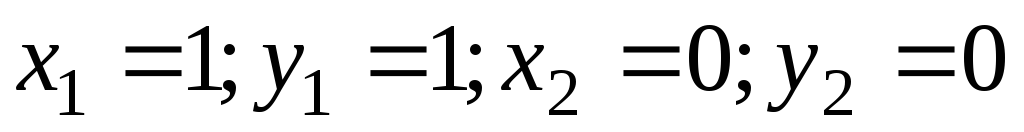 ;
;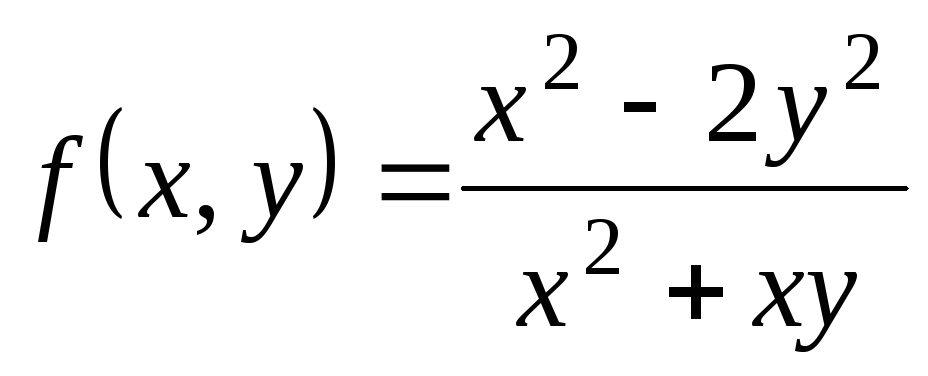 ,
, 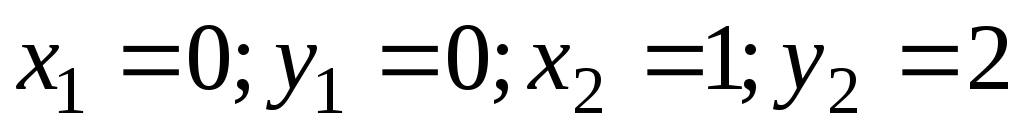 ;
;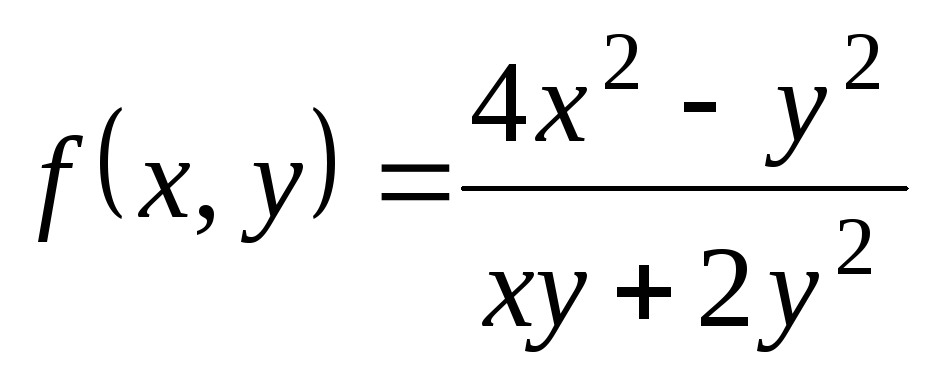 ,
, 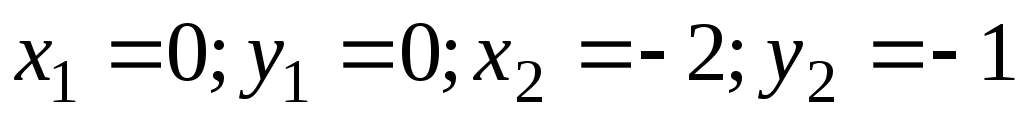 ;
;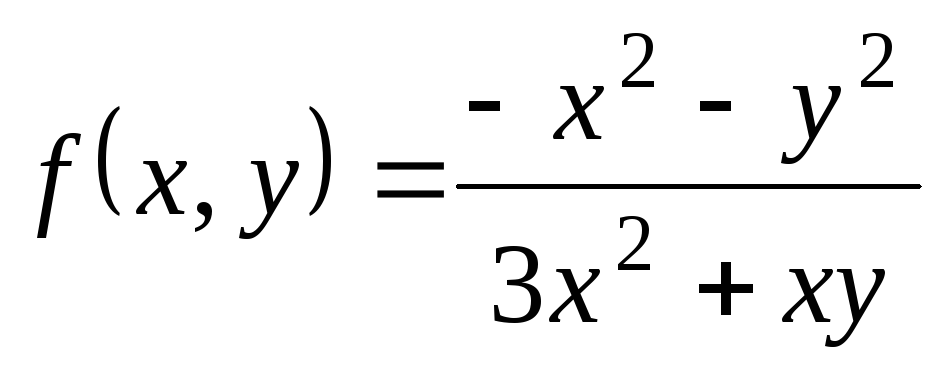 ,
, 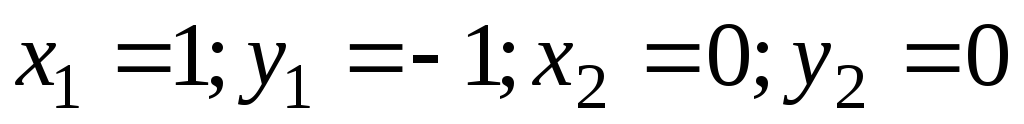 ;
;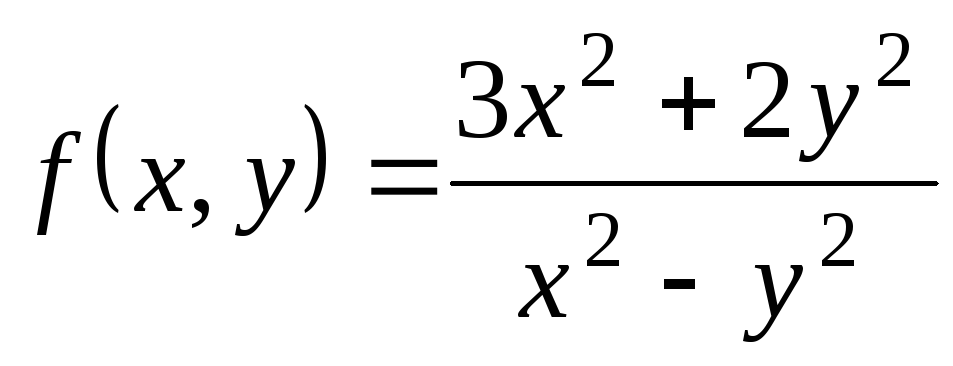 ,
, 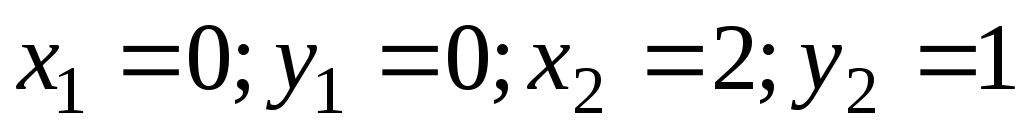 ;
;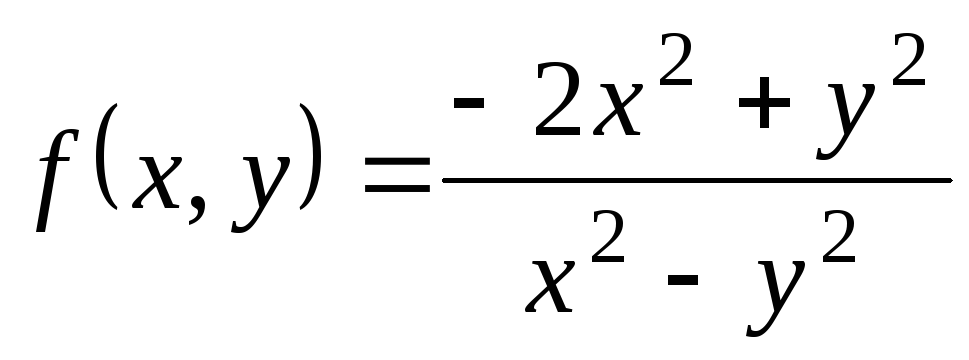 ,
,
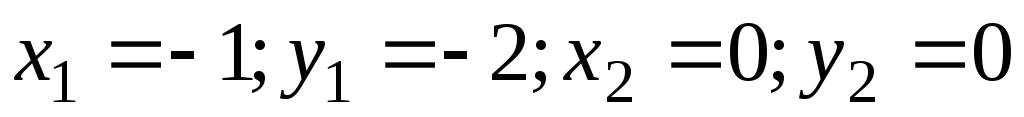 ;
;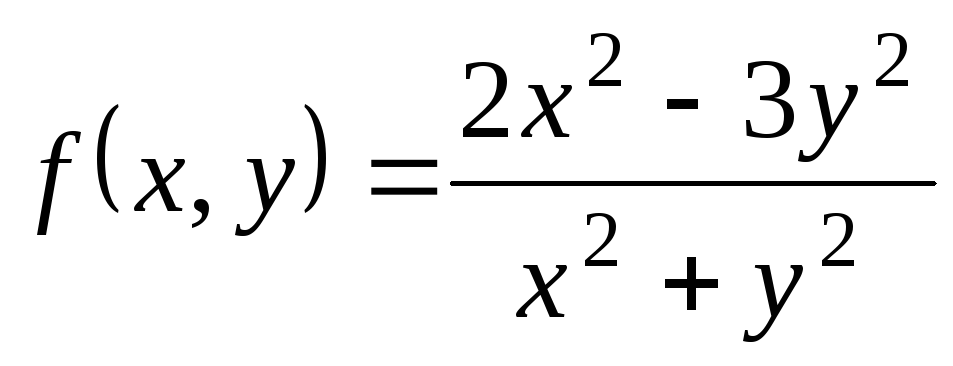 ,
, 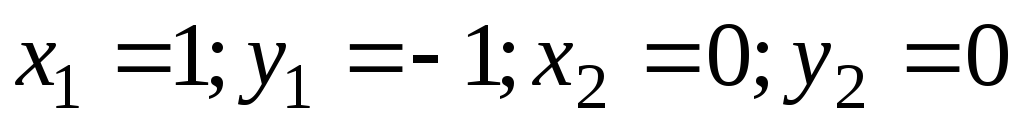 ;
;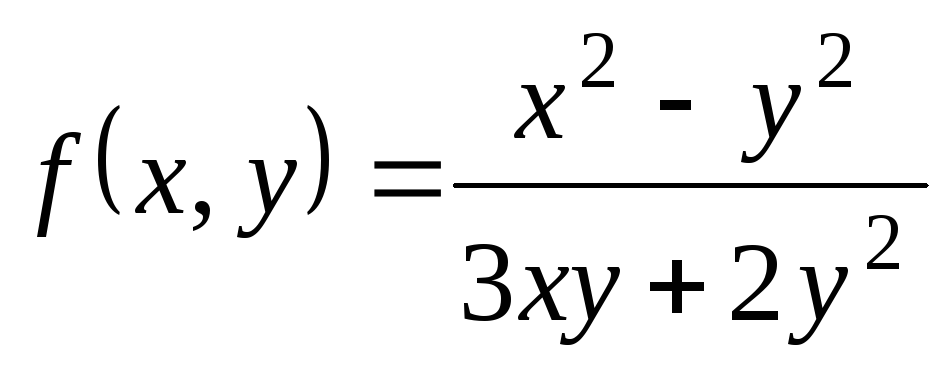 ,
, 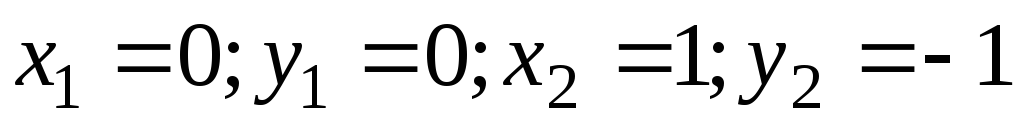 .
.
ЗАДАНИЕ 4
Найдите
![]() для функции
для функции![]() и значение частной производной в
указанной точке (M):
и значение частной производной в
указанной точке (M):
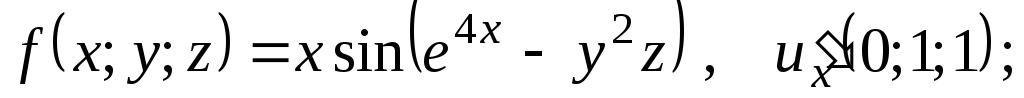 2)
2)
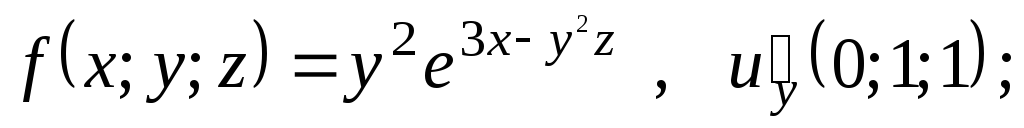
3)
![]() 4)
4)![]()
5)![]() 6)
6)![]()
7)![]() 8)
8)![]()
9)![]() 10)
10)![]() .
.
ЗАДАНИЕ 5
Найдите частные
производные функции
![]() .
В ответе приведите
значения
частных производных
.
В ответе приведите
значения
частных производных
![]() ,
,![]() ,
,![]() для данной функции
для данной функции![]() в точке
в точке![]() с точностью до двух знаков после запятой:
с точностью до двух знаков после запятой:
1.
![]() ;
2.
;
2.![]() ;
;
3.
![]() ;
4.
;
4.![]() ;
;
5.
![]() ;
6.
;
6.![]() ;
;
7.![]() ;
8.
;
8.![]() ;
;
9.
![]() ;
10.
;
10.![]() .
.
ЗАДАНИЕ 6
Найдите
все частные производные второго порядка
функции
![]() .
Найдите значения указанной частной
производной в указанной точке:
.
Найдите значения указанной частной
производной в указанной точке:
10)![]() .
.
ЗАДАНИЕ 7
Найти все частные производные второго порядка следующих функций.
Доказать, что
![]() :
:
|
1)
|
2)
|
|
3)
|
4) |
|
5)
|
6)
|
|
7)
|
8)
|
|
9)
|
10)
|
ЗАДАНИЕ 8
Найти все частные
производные второго порядка следующих
функций. Доказать, что
![]() :
:
|
1)
|
2)
|
|
3)
|
4)
|
|
5)
|
6)
|
|
7)
|
8)
|
|
9)
|
10)
|
ЗАДАНИЕ 9
Докажите, что функция ![]() удовлетворяет условию
удовлетворяет условию
![]()
1)![]()
2)![]()
3)![]() 4)
4)![]()
5)![]() 6)
6)![]()
7)![]() 8)
8)![]()
9)![]() 10)
10)![]() .
.
ЗАДАНИЕ 10
Дана функция
![]() Проверить, удовлетворяет ли она данному
уравнению.
Проверить, удовлетворяет ли она данному
уравнению.
|
№ |
|
Уравнение |
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
ЗАДАНИЕ 11
Дана функция
![]() .
Показать, что
.
Показать, что
![]() .
.
1)
![]() ;
;
![]() ;
;
2)
![]() ;
;
![]() ;
;
3)
![]() ;
;
![]() ;
;
4)
![]() ;
;
![]() ;
;
5)
![]()
![]() ;
;
6)
![]() ;
;
![]() ;
;
7)
![]() ;
;
![]() ;
;
8)
![]() ;
;
![]() ;
;
9)
![]() ;
;
![]() ;
;
10)![]() ;
;
![]() .
.
ЗАДАНИЕ 12
Найдите du
и
![]() для функции
для функции
![]() :
:
1)![]() ;
2)
;
2)![]() ;
;
3)![]() ;
4)
;
4)![]() ;
;
5)![]() ; 6)
; 6)![]() ;
;
7)![]() ; 8)
; 8)![]() ;
;
9)![]() ; 10)
; 10)![]() .
.
ЗАДАНИЕ 13
Составьте уравнение
касательной плоскости и нормали к
поверхности, заданной уравнением f(x;
y;
z)=0
в указанной точке
![]() :
:
1)![]() ;
;
2)![]() ;
;
3)![]() ;
;
4)![]() ;
;
5)![]() ;
;
6)![]() ;
;
7)![]() ;
;
8)![]() ;
;
9)![]() ;
;
10)![]() .
.
ЗАДАНИЕ 14
Дана функция
![]() и точка M0(x0;y0).
С помощью дифференциала вычислить
приближенное значение функции в данной
точке. Оценить абсолютную погрешность
вычислений:
и точка M0(x0;y0).
С помощью дифференциала вычислить
приближенное значение функции в данной
точке. Оценить абсолютную погрешность
вычислений:
1)
![]() ;M0(1,08;1,94);
;M0(1,08;1,94);
2)
![]() ; M0(3,04;3,95);
; M0(3,04;3,95);
3)
![]() ; M0(2,98;2)05);
; M0(2,98;2)05);
4)
![]() ; M0(1,06;2,92);
; M0(1,06;2,92);
5)
![]() ; M0(2,94;1,07);
; M0(2,94;1,07);
6)
![]() ; M0(1,96;1,04);
; M0(1,96;1,04);
7)
![]() ; M0(0,96;1,95);
; M0(0,96;1,95);
8)
![]() ; M0(3,96;1,03);
; M0(3,96;1,03);
9)
![]() ; M0(0,97;2,03);
; M0(0,97;2,03);
10)
![]() ; M0(2,98;3,91).
; M0(2,98;3,91).
ЗАДАНИЕ 15
Пользуясь правилом
дифференцирования сложной функции,
найдите![]() для
заданных функций
для
заданных функций![]()
![]()
![]() .
.
1) ![]()
![]()
![]() ;
;
2) ![]()
![]()
![]() ;
;
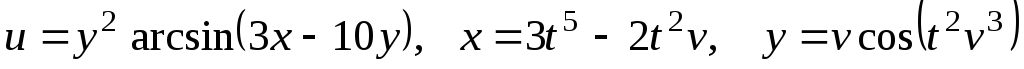 ;
;
4) ![]() ;
;
5) ![]() ;
;
6) ![]() ;
;
7) ![]() ;
;
8) ![]() ;
;
9) ![]() ;
;
10) ![]() .
.
ЗАДАНИЕ 16
Вычислить производные сложных функций:
1)
![]() где
где![]()
![]()
![]()
![]()
2)
![]() где
где![]()
![]()
![]()
3)
![]() ,
где
,
где![]() ,
,![]()
![]()
4)
![]() ,
где
,
где![]()
![]() ;
;![]()
5)
![]() где
где![]()
![]()
![]()
6)
![]() где
где![]()
![]() ;
;![]()
7)
![]() где
где![]()
![]() ;
;![]()
![]()
8)
![]() где
где![]() ,
,![]()
![]()
9)
![]() где
где![]() ,
,![]() ;
;![]()
10)
![]() где
где![]()
![]() ;
;![]()
ЗАДАНИЕ 17
Найдите![]() для
функции, заданной неявно:
для
функции, заданной неявно:
1)
![]() ;
2)
;
2)![]() ;
;
3)
![]() ; 4)
; 4)![]() ;
;
5)
![]() ;
6)
;
6)![]() ;
;
7)
![]() ;
8)
;
8)![]() ;
;
9)
![]() ;
10)
;
10)![]() .
.
ЗАДАНИЕ 18
Найдите
![]() для функции
для функции![]() ,
заданной неявно указанным уравнением:
,
заданной неявно указанным уравнением:
1)
![]() ; 2)
; 2)![]() ;
;
3)
![]() ; 4)
; 4)![]() ;
;
5)
![]() ; 6)
; 6)![]() ;
;
7)
![]() ; 8)
; 8)![]() ;
;
9)
![]() ; 10)
; 10)![]() .
.
ЗАДАНИЕ 19
Продифференцировать: а) сложную функцию; б) функцию заданную неявно:
1. а)
![]() ,где
,где
![]() ;
;
б)
![]() .
.
2. а)
![]() ,где
,где
![]() ;
;
б)
![]() .
.
3. а)
![]() ,где
,где
![]() ;
;
б)
![]() .
.
4. а)
![]() ,где
,где
![]() ;
;
б)
![]() .
.
5. а)
![]() ,где
,где
![]() ;
;
б)
![]() .
.
6. а)
![]() ,где
,где
![]() ;
;
б)
![]() .
.
7. а)
![]() ,где
,где
![]() ;
;
б)
![]() .
.
8. а)
![]() ,где
,где
![]() ;
;
б)
![]() .
.
9. а)
![]() ,где
,где
![]() ;
;
б)
![]() .
.
10. а)
![]() ,где
,где
![]() ;
;
б)
![]() .
.
ЗАДАНИЕ 20*
Найдите якобиан
![]() заданной системы функций:
заданной системы функций:
1)
![]() 2)
2)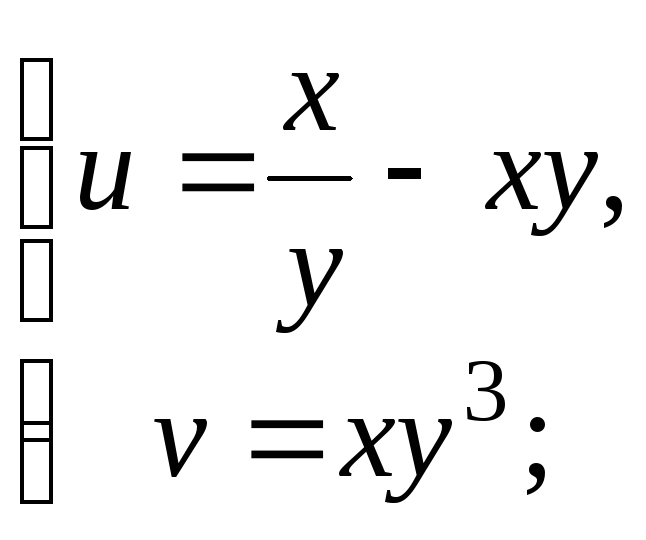
3)
![]() 4)
4)![]()
5)
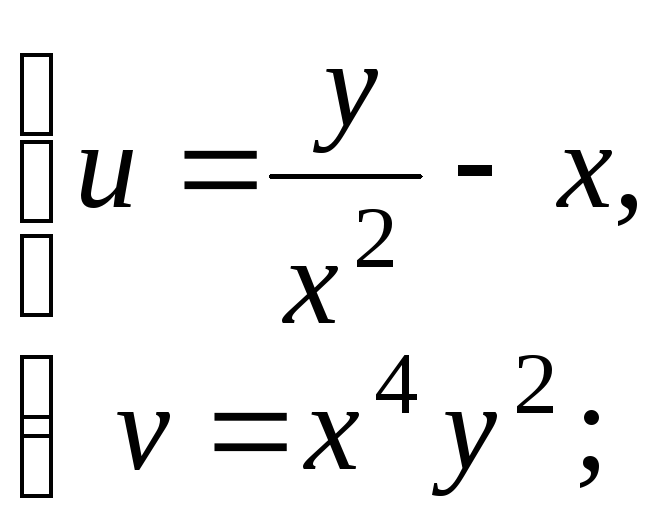 6)
6)![]()
7)
![]() 8)
8)![]()
9)
![]() 10)
10)![]() .
.
ЗАДАНИЕ 21*
Функции
![]() независимых переменныхx
и y
заданы неявно системой уравнений.
Найдите
независимых переменныхx
и y
заданы неявно системой уравнений.
Найдите
![]() ,
,![]() :
:
1)
![]() 2)
2)![]()
3)
![]() 4)
4)![]()
5)
![]() 6)
6)![]()
7)
![]() 8)
8)![]()
9)
![]() 10)
10)![]() .
.
ЗАДАНИЕ 22*
В декартовой прямоугольной системе координат Оxy область (D) задана системой неравенств. Найдите область (G) в системе координат O'uv, в которую перейдет (D) в результате преобразования координат
![]()
|
№ п/п |
Неравенства, задающие область (D) |
Уравнения преобразования координат |
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
|
11 |
|
|
ЗАДАНИЕ 23
В декартовой
прямоугольной системе координат Оxy
область (D)
задана системой неравенств. Найдите
область (G)
в системе координат O'uv
, в которую перейдет (D)
в результате преобразования координат
![]()
|
№ п/п |
Неравенства, задающие область (D) |
Уравнения преобразования координат |
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
ЗАДАНИЕ 24
Найдите
![]() и
и![]() в точке
в точке![]() :
:
1)![]() ; 2)
; 2)![]() ;
;
3)
![]() ;4)
;4)
![]() ;
;
5)
![]() ;6)
;6)
![]() ;
;
7)
![]() ;
8)
;
8)![]() ;
;
9)
![]() ;
10)
;
10)![]() .
.
ЗАДАНИЕ 25
Дана функция
![]() ,
точкаA(x0,y0)
и вектор
,
точкаA(x0,y0)
и вектор
![]() .
Найдите
.
Найдите
1) grad
z
в точке A;
2) производную в точке A
по направлению вектора
![]() :
:
1)
![]() ;
; ![]() ;
; ![]() ;
;
2)
![]() ;
; ![]() ;
; ![]() ;
;
3)
![]() ;
; ![]() ;
; ![]() ;
;
4)
![]() ;
; ![]() ;
; ![]() ;
;
5)
![]() ;
;
![]() ;
; ![]() ;
;
6)
![]() ;
;
![]() ;
; ![]() ;
;
7)
![]() ;
;
![]() ;
; ![]() ;
;
8)
![]() ;
; ![]() ;
; ![]() ;
;
9)
![]() ;
; ![]() ;
;
![]() ;
;
10)
![]() ;
; ![]() ;
; ![]() .
.
ЗАДАНИЕ 26
Дана функция
![]() .
Найти в точке
.
Найти в точке![]() производную по направлению
производную по направлению![]() ,
градиент функции и его модуль:
,
градиент функции и его модуль:
1)
![]()
![]() ,
,![]() ,
,![]() ;
;
2)
![]()
![]() ,
,![]() ,
,![]() ;
;
3)
![]()
![]() ,
,![]() ,
,![]() ;
;
4)
![]()
![]() ,
,![]() ,
,![]() ;
;
5)
![]()
![]() ,
,![]() ,
,![]() ;
;
6)
![]()
![]() ,
,![]() ,
,![]() ;
;
7)
![]()
![]() ,
,![]() ,
,![]() ;
;
8)
![]()
![]() ,
,![]() ,
,![]() ;
;
9)
![]()
![]() ,
,![]() ,
,![]() ;
;
10)
![]()
![]() ,
,![]() ,
,![]() .
.
ЗАДАНИЕ 27
Даны функция трех переменных u = f (x, y, z), точка M0 (x0; y0; z0) и вектор
![]() (а1,
а2,
а3)
. Найдите 1) grad
u в точке М0;
2) производную в точке М0
по направлению вектора
(а1,
а2,
а3)
. Найдите 1) grad
u в точке М0;
2) производную в точке М0
по направлению вектора
![]() :
:
1)
![]() M0 (1;
-2; 1) ;
M0 (1;
-2; 1) ; ![]() (-1;
2; 2) ;
(-1;
2; 2) ;
2)
u = ln|3x2
– 2y + z| ; M0
(1; 1; 0) ; ![]() (0;
4; 3) ;
(0;
4; 3) ;
3)
![]() M0 (1;
1; 2) ;
M0 (1;
1; 2) ; ![]() (-3;
0; 4) ;
(-3;
0; 4) ;
4)
![]() M0 (1;
2; 2) ;
M0 (1;
2; 2) ; ![]() (3;
0; -4) ;
(3;
0; -4) ;
5)
![]() M0 (2;
2; 1) ;
M0 (2;
2; 1) ; ![]() (1;
-2; 2) ;
(1;
-2; 2) ;
6)
u = ln|10 – x2
– y2
– z2|
; M0 (2;
2; 1) ; ![]() (-4;
0; 3);
(-4;
0; 3);
7)
![]() M0 (3;
4; 0) ;
M0 (3;
4; 0) ; ![]() (2;
-1; 2) ;
(2;
-1; 2) ;
8)
u = x2y2
+ x2z2
+ y2z2
; M0
(-1; 2; 1) ; ![]() (0;
6; 8);
(0;
6; 8);
9)
![]() M0 (3;
4; 0) ;
M0 (3;
4; 0) ; ![]() (2;
2; -1) ;
(2;
2; -1) ;
10)
u = ln|12 – x2
– y2
+ z| ; M0
(1; 1; -5) ; ![]() (3;
0; -4) .
(3;
0; -4) .