11. Ряды Фурье
Система непрерывных
на отрезке [a;
b]
функций
называетсяортонормированной,
если
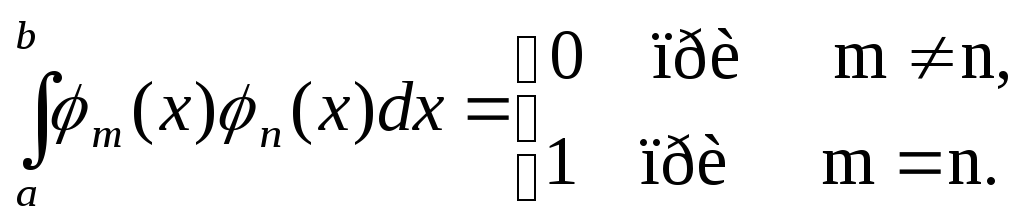
Примером ортонормированных систем являются:
1)
,
,
,
,
,
. . . ,
,
,
. . .
на отрезке [– ; ];
2)
,
,
,
,
,
... ,
,
,
...на отрезке [a;
b
]; здесь T
= b
– a,
;
3) система полиномов Лежандра
,
,
n
= 1, 2, 3, ... на отрезке [–1; 1 ].
Имеется множество других примеров ортонормированных систем функций. Ортонормированные системы функций играют роль ортонормированного базиса в некотором пространстве Гильберта функций, определённых на промежутке [a, b]. Любой функции f(x) из этого пространства ставится в соответствие ряд
~
, (1)
где Ck находится по формуле
,
k
= 0, 1, 2, .... (2)
При этом коэффициенты Ck, вычисляемые по формулам (2), называются коэффициентами Фурье функции f(x), а ряд (1) – рядом Фурье функции f(x).
Важную роль играют
полные ортонормированные системы
функций. Говорят, что функция f(x),
определённая на промежутке [a;
b],
является функцией с интегрируемым
квадратом,
если f(x)
и
интегрируемы на [a;
b]
(интеграл может быть и несобственным).
Теорема.
Пусть
– ортонормированная система функций
на промежутке [a;
b].
Следующие утверждения равносильны:
для любой функции f(x) с интегрируемым квадратом справедливо равенство
,
где
Ck
– коэффициенты Фурье по системе
;
для любой функции f(x) с интегрируемым квадратом
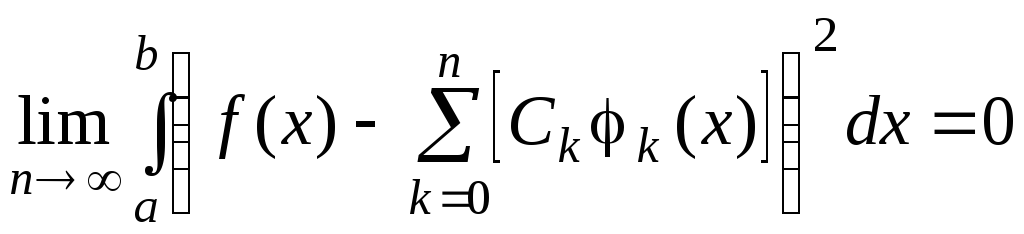
(при выполнении этого равенства говорят, что ряд Фурье функции f(x) сходится к f(x) в среднем);
3)
если f(x)
– функция с интегрируемым квадратом и
для любого k 
,
то
.
Ортонормированная система функций, обладающая любым из условий 1), 2), 3) (а следовательно, и двумя другими), называется полной.
Приведённые выше примеры ортонормированных систем функций обладают свойством полноты.
Если
– полная ортонормированная система
функций, то для любой функции с
интегрируемым квадратом на [a,
b],
знак «~» в формуле (1) можно в некотором
смысле заменить на «=» (фразу «в некотором
смысле» проясняет пункт 2) в формулировке
теоремы).
Будем говорить, что функции f(x) и g(x) с интегрируемым квадратом на [a, b] равны в смысле среднеквадратичного отклонения, если
,
и будем при этом писать f(x) =c.o. g(x).
Теорема.
Пусть
– ортонормированная система функций
на [a;
b]
и пусть f(x)
и g(x)
– функции с интегрируемым квадратом
на [a;b].
Тогда f(x)
= c.o.
g(x)
на [a;
b]
в том и только в том случае, если
коэффициенты Фурье функций f(x)
и g(x)
совпадают.
Чаще других применяют тригонометрическую ортонормированную систему
,
,
,
,
,
... ,
,
,
...
на
[a;
b],
T
= b
– a,
.
Ряд Фурье по системе этих функций обычно
называют тригонометрическим
рядом Фурье:
,
, n
= 0, 1, 2, ... ,
, n
= 1, 2, 3, ... .
Функция f(x)
называется кусочно-монотонной
на отрезке [a;
b],
если этот отрезок можно разбить на
конечное число интервалов
,
в каждом из которыхf(x)
монотонна. Аналогично определяется
понятие кусочно-непрерывной функции
при этом слово «монотонность» заменяется
на «непрерывность».
Теорема (Дирихле). Если функция f(x), определённая на отрезке [a;b] является на нём кусочно-непрерывной, кусочно-монотонной и ограниченной, то её тригонометрический ряд сходится во всех точках отрезка [a;b] к некоторой функции S(x). Кроме того:
1) если x – точка непрерывности функции f(x), то S(x) = f(x);
2) если x – точка разрыва (устранимая или первого рода) функции f(x), то
;
3)
.
Типовой пример
Разложить в тригонометрический ряд Фурье функцию
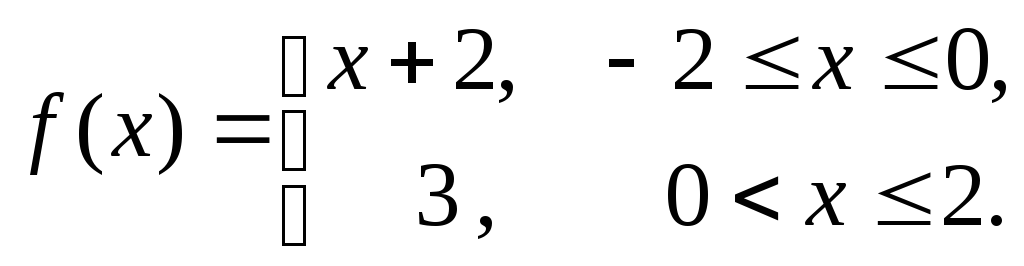
►Заданная
функция кусочно-непрерывна, кусочно-монотонна
и ограничена на [–2, 2], следовательно,
её можно разложить в тригонометрический
ряд Фурье. Найдём коэффициенты Фурье.
Имеем T
= 4,
.
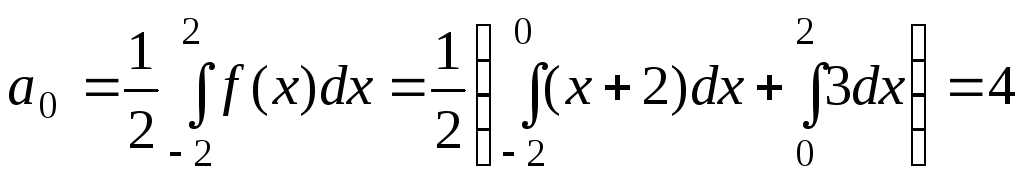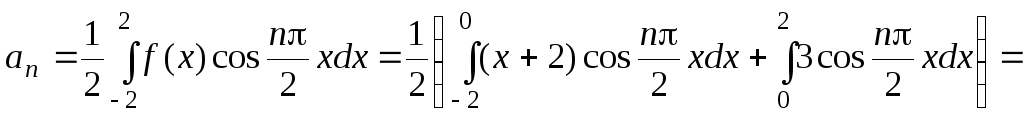
, n
= 1, 2, 3, ... ,
.
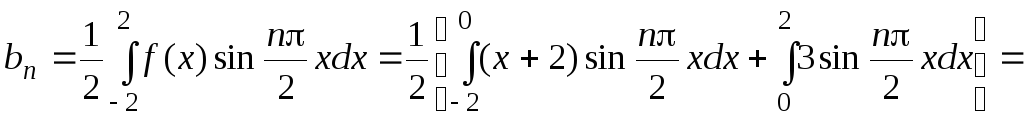
Таким образом,
.
Причём
◄
Типовой пример
Разложить в тригонометрический ряд Фурье функцию
,
–1 < x
< 2.
►Данная функция удовлетворяет условиям теоремы Дирихле. Ввиду непрерывности f(x) на (–1; 2)
.
Имеем
T
= 3,
.
Найдём коэффициенты an
и bn.
.
,
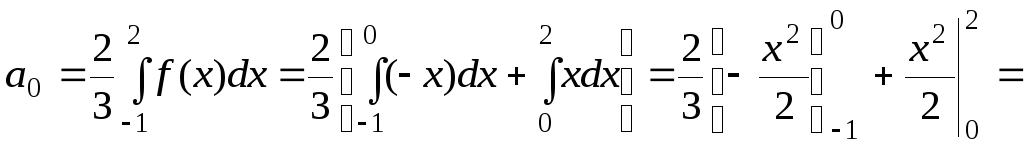
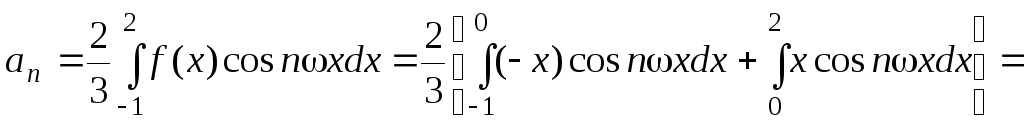
n = 1, 2, 3, ... ,
.
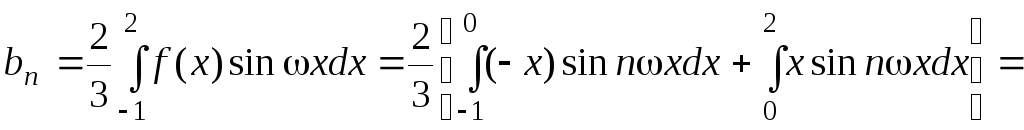
Таким образом,
, –1
< x
< 2,
где an, bn, n 1 найдены выше.◄
Если функция f(x),
определённая на интервале
и удовлетворяющая условиям теоремы
Дирихле, является чётной, то в её
разложении в ряд Фурье будут участвовать
лишь косинусы:
,
т.е.
все
окажутся равными нулю. Если жеf(x)
является нечётной функцией на
,
то её ряд Фурье будет содержать лишь
синусы:
.
Если
ставится задача разложить функцию f(x),
определённую на интервале
в ряд по косинусам, то её доопределяют
на интервале
чётным образом и разлагают новую функциюf1(x)
в тригонометрический ряд Фурье на
интервале
;
этот ряд Фурье будет содержать лишь
косинусы. Ввиду того, чтоf(x)
и f1(x)
совпадают на
,
при этом получается разложение функцииf(x)
в ряд по косинусам
,
где
.
Аналогично,
если требуется разложить функцию f(x),
определённую на
в ряд по синусам, тоf(x)
продолжают на
нечётным образом и разлагают новую
(нечётную) функциюf2(x)
в тригонометрический ряд Фурье на
интервале
;
этот ряд будет содержать лишь синусы.
В результате получим разложениеf(x)
в ряд по синусам:
,
где
.
Типовой пример
Разложить функцию
,
определённую на интервале
,
в ряд Фурье: а) по косинусам; б) по синусам.
►а) Имеем
, 
.
Запишем разложение f(x) в ряд по косинусам:
, 0
< x
< .
б) Имеем
.
Отсюда получаем разложение f(x) в ряд Фурье по синусам:
, 0
< x
< .◄
Ещё одним важным примером ортонормированной системы функций является
на
отрезке [a;b];
здесь, как и прежде T
= b
– a,
.
Любую функцию, удовлетворяющую условиям
теореме Дирихле, можно разложить в ряд
Фурье по этой системе (при этом справедлива
теорема Дирихле):
. (14)
Коэффициенты Фурье находятся по формуле
.
Ряд
(14) называется рядом
Фурье в комплексной форме.
При этом между Cn
и коэффициентами Фурье an,
bn
функции f(x)
ортонормированной системы
существует следующая связь:
,
,
.
Типовой пример
Разложить функцию f(x) = x на интервале (0; ) в ряд Фурье в комплексной форме.
►В нашем случае T = , = 2. Имеем
,
.
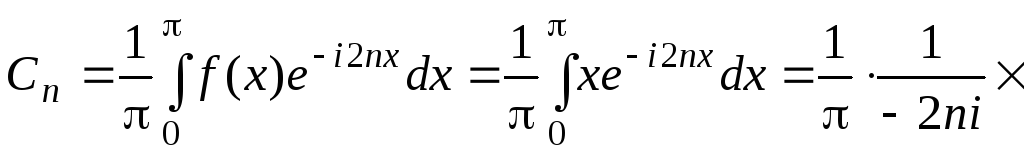
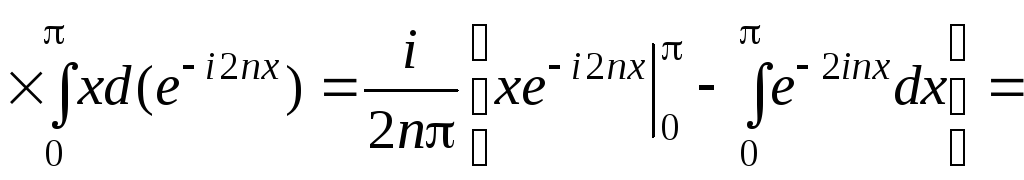
Таким образом,
.◄