5. Ряд Тейлора

Мы доказали, что сумма степенного ряда в любой точке интервала сходимости бесконечно дифференцируема. Выразим коэффициенты ряда через производные суммы

. Положим здесь . Все члены ряда, кроме нулевого, исчезают, и.

. Положим , тогда.

. .

. .

Продолжая этот процесс, получим . Заменив коэффициенты полученными выражениями, представим ряд как

.

Ряд, стоящий в правой части этой формулы, называется рядом Тейлора функции . В частном случае, когдаи ряд принимает вид

, его принято называть рядом Маклорена. Напомним, что эти ряды получены в предположении, что - сумма степенного ряда их - точка интервала сходимости.

Теперь рассмотрим обратную задачу: какой должна быть функция , чтобы её можно было представить в виде суммы степенного ряда? Первое, что очевидно, это то, чтодолжна быть бесконечно дифференцируемой функцией (так как сумма ряда бесконечно дифференцируема). Второе - то, что коэффициенты ряда должны быть равны. Поэтому предположим, что дана бесконечно дифференцируемая функция, мы нашли коэффициенты ряда по формуле, составили формальный ряди нашли область его сходимости. Будет ли сумма этого ряда на области сходимости равна?

ТЕОРЕМА. Для того, чтобы бесконечно дифференцируемая функция в окрестности точкиразлагалась в ряд Тейлора, необходимо и достаточно, чтобы, т.е. остаток ряда стремится к нулю при .

6. Разложение в ряд Маклорена элементарных функций

,

,

,

7. Решение задач на разложение функций в ряд

Большинство задач, в которых требуется разложить элементарную функцию в ряд по степеням , решается применением стандартных разложений. К счастью, любая основная элементарная функция имеет свойство, которое позволяет это сделать.

Типовые примеры

1. Разложить функцию по степеням.

►Имеем. Ряд сходится при.◄

2. Разложить функцию по степеням.

►Имеем . Область сходимости:.◄

3. Разложить функцию по степеням.

►Имеем . Ряд сходится при.◄

4. Разложить функцию по степеням.

►Имеем . Ряд сходится при.◄

5. Разложить функцию по степеням.

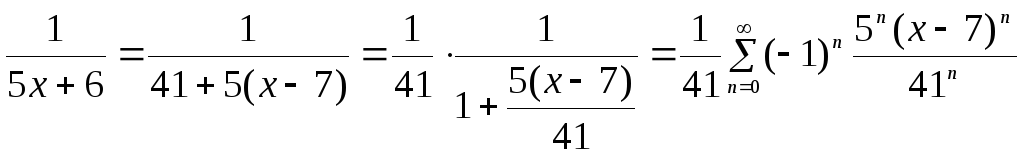►Имеем. . Область сходимости.◄

6. Разложить функцию по степеням.

►Разложение в ряд простых рациональных дробей второго типа получается почленным дифференцированием соответствующих разложений дробей первого типа. В этом примере

◄

7. Разложить функцию по степеням.

►Если рациональная дробь не является простой, она сначала представляется в виде суммы простых дробей: , а затем действуем, как в примере 5: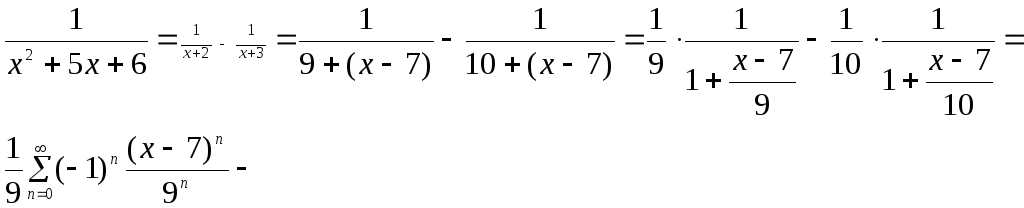, где.◄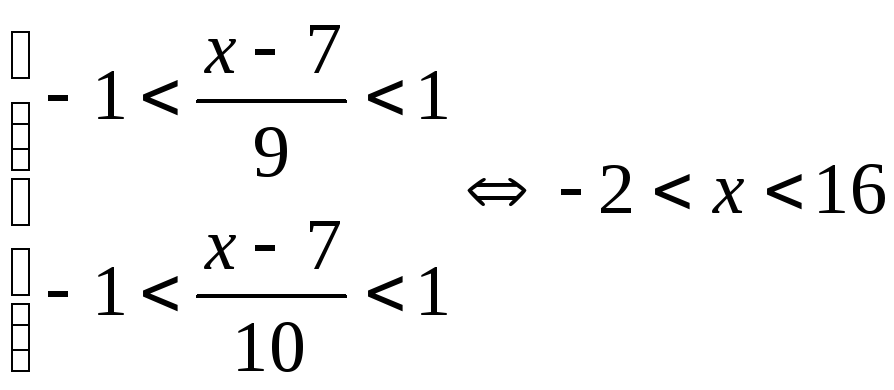

8. Разложить в ряд Тейлора в окрестности функцию.

►Разложим в ряд производную данной функции , воспользовавшись табличным разложением для функции. Имеем

. Проинтегрировав общий член полученного ряда, и, учитывая, что y(0)=0, получим искомое разложение: .◄

9. Разложить функцию в ряд Тейлора по степеням х.

►Разложим на элементарные дроби

Воспользуемся готовой формулой

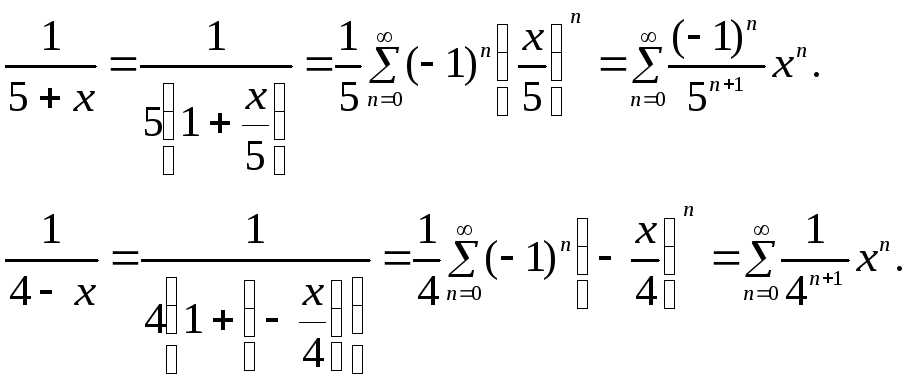
Сложив эти два выражения, окончательно получим

.◄