ГЛАВА. Числовые и функциональные ряды

§1. Числовые ряды. Свойства сходящихся рядов

1. Пусть бесконечная числовая последовательность с вещественными или комплексными членами.

Выражение

(1)

называется числовым рядом, числа – элементами (членами) ряда. Формула, по которой в зависимости от номера члена ряда получается числовое значение этого члена, называется общим членом ряда.

Сумма n первых членов ряда (1) называется n-й частичной суммой этого ряда.

Например, - первая, вторая, третья частичные суммы ряда. Очевидно, что частичные суммы составляют бесконечную последовательность.

Ряд (1) называется сходящимся, если последовательность его частичных сумм имеет конечный предел

(2)

Этот предел s называется суммой ряда (1).

Если предел (2) не существует или бесконечен, то ряд (1) называется расходящимся.

Ряд , членами которого являются все члены ряда (1), начиная с-го , без изменения их порядка, называетсяn-м остатком ряда (1). Обозначают .

Типовой пример

Исследовать на сходимость ряд, полученный суммированием членов бесконечной геометрической прогрессии, ,. (3)

►Если , то частичная сумма ряда (3) будет. Пусть, тогда= =. Следовательно, ряд (3) сходится. Пусть , тогдаи ряд (3) расходится. Приполучим рядa+a+a+..., . Очевидно, такой ряд расходится.

При , получим рядa–a+a–a+....

Очевидно, предела не имеет и ряд расходится.◄

Типовые примеры

1) Найти сумму ряда .

►Общий член ряда . Эту дробь можно представить в виде суммы двух простых дробей

.

Поэтому n-ю частичную сумму ряда можно записать следующим образом:

.

Имеем .◄

2) Найти сумму ряда

►Составим последовательность частных сумм

,

,

,

тогда, если , то.

Следовательно, .◄

Задача Доказать непосредственно сходимость ряда и найти его сумму:

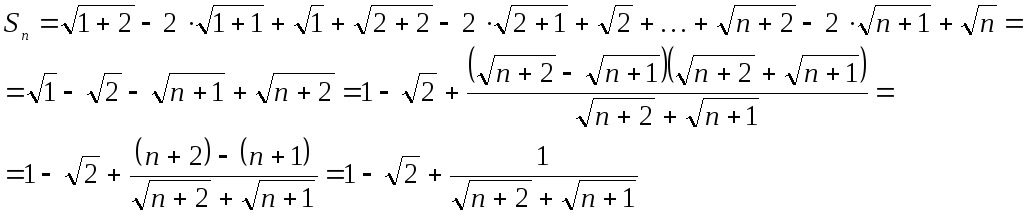► Следовательно,. ◄ ТЕОРЕМА 1. Ряд сходится тогда и только тогда, когда сходится его некоторый остаток.

Сделаем вывод из этого свойства: отбрасывание конечного числа начальных членов ряда или добавление в его начало нескольких новых членов не влияет на сходимость ряда.

Типовой пример

Доказать, что ряд сходится и найти его сумму.

►Ранее была получена формула Тейлора для функции

, (5)

и доказано, что при.Подставляя в (5), получаем

. (6)

Здесь – частичная сумма полученного числового ряда, а остаточный членявляетсяn-ым остатком этого ряда. Поскольку при всех , то, согласно теореме 1, ряд сходится, а его сумма равна.◄

2. ТЕОРЕМА (необходимое условие сходимости). Если ряд сходится, то.

Следствие

Если , то ряд расходится.

Типовые примеры

1) Исследовать на сходимость гармонический ряд .

►Имеем .

Предположим, что гармонический ряд сходится. Тогда , нопри любом. Получили противоречие. Следовательно, наше предположение о сходимости гармонического ряда неверное. Он расходится. ◄

2) Исследовать сходимость ряда .

►Поскольку , то ряд расходится, т.к. не выполнено необходимое условие. ◄

Отметим без доказательства следующие свойства сходящихся рядов.

1. Если , то, т.е. сходящиеся ряды можно умножать на число.

2. Если ,, то. т.е. сходящиеся ряды можно почленно складывать и вычитать.

Сходящиеся ряды обладают сочетательным (ассоциативным) свойством. Если объединить члены сходящегося ряда в произвольные группы, заключая члены ряда в скобки, не меняя их местоположения, то сумма ряда не изменится. Заметим, что опускать скобки нельзя. Например, ряд (1–1)+(1–1)+... сходится, а ряд 1–1+1–1+... расходится.