
Министерство образования и науки РФ
 Пензенский
государственный университет
Пензенский
государственный университет
Кафедра «Автоматика и телемеханика»
Автоматические системы
Пояснительная записка к курсовой работе
по дисциплине «Теория автоматического управления»
выполнила:
ст. гр. 11ПА1
Каренкова А.Ю.
проверила:
доцент
Алексеева М.Б
Пенза 2013 год
 Задание
к курсовой работе
Задание
к курсовой работе
-
Составить систему 3-го порядка из типовых звеньев, задав их коэффициенты самостоятельно.
-
Записать для заданной системы дифференциальное уравнение и передаточную функцию. Синтезировать аналитические выражения для ее АЧХ и ФЧХ.
-
С использованием какого-либо программного средства построить переходную, АЧХ и ФЧХ характеристики.
-
Записать нули и полюса системы и отобразить их на координатной плоскости.
-
Оценить устойчивость системы с использованием критериев Гурвица, Найквиста и Михайлова.
 Реферат
Реферат
Пояснительная записка содержит 19 листов формата А4, 2 рисунка, 1 приложение, 1 источник.
АВТОМАТИЧЕСКАЯ СИСТЕМА, ПЕРЕДАТОЧНАЯ ФУНКЦИЯ, КОЭФФИЦИЕНТ ПЕРЕДАЧИ, УСТОЙЧИВОСТЬ СИСТЕМЫ.
Цель работы – записать передаточные функции замкнутой и разомкнутой систем, для заданной динамической системы определить временные и частотные характеристики, найти полюса и нули системы, определить устойчивость системы.
Содержание
Введение
………………………………………………………………
 5
5
-
 Составление
системы 3-го порядка из типовых звеньев…….6
Составление
системы 3-го порядка из типовых звеньев…….6 -
Составление для заданной системы дифференциального
уравнения и передаточной функции. Синтез данных
аналитических выражений для ее
АЧХ и ФЧХ ………………………………………………………. 7
-
Построение переходной, импульсной, АЧХ и ФЧХ
характеристик в MATLAB…………………………………….8
-
Нахождение нулей и полюсов системы ……………………...8
-
Определение устойчивости системы по
критериям Найквиста, Гурвица, Михайлова…………………..9
-
Определение устойчивости по критерию Найквиста…….9
-
Определение устойчивости по критерию Гурвица……..11
-
Определение устойчивости по критерию Михайлова….12
-
Вывод по работе………………………………………………..13
-
Список использованных источников…………………………14
-
Приложение А
 Введение
Введение
В нашу жизнь прочно вошли автоматические системы управления. Данные системы могут использоваться в различных областях жизни и деятельности человека. Виды их соответствуют основным классификационным признакам. В данной курсовой работе мы проектируем автоматическую систему, состоящую из последовательно соединенных звеньев, строим ее основные характеристики, решаем вопрос об устойчивости данной системы.
-
Составление системы 3-го порядка из типовых звеньев
Задаем таблицу коэффициентов для передаточных функций:
Таблица 1
-
К1
К2
К3
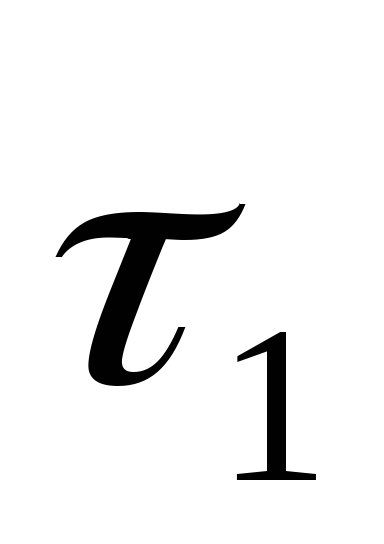
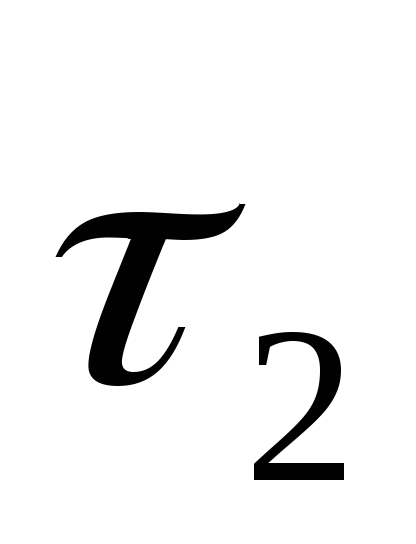
5
3
1
0.14
0.01
Задаем передаточные функции для звеньев системы:
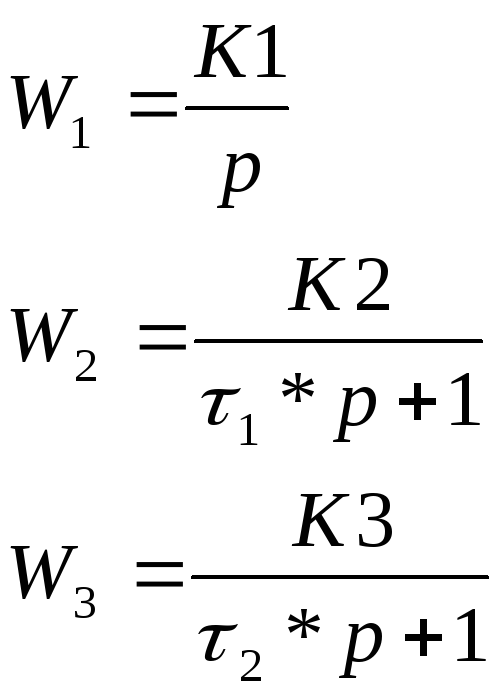 -
идеальное интегрирующее звено
-
идеальное интегрирующее звено
 -
инерционное звено
-
инерционное звено
- инерционное звено
Мы составили автоматическую систему 3-го порядка.

Рисунок 1
Система 3-го порядка
-
Составление для заданной системы дифференциального уравнения и передаточной функции. Синтез данных аналитических выражений для ее АЧХ и ФЧХ
Составим передаточную функцию для разомкнутой системы:
Т.к. соединение звеньев последовательное, передаточные функции звеньев перемножаются:
![]()
![]() ,
,
где К=К1*К2*К3 Запишем передаточную функцию замкнутой системы:
![]()
![]() =
=![]()
Посчитаем значение коэффициентов:
а![]() =
=![]() =
0.0014
=
0.0014
 а
а![]() =
=![]()
К=К1*К2*К3=5*3*1=15
Составим дифференциальное уравнение для заданной системы:
а![]() *
*![]()
![]() +
+
![]() +
+![]() =K*X
=K*X![]()
Синтезируем выражения для АЧХ и ФЧХ:
Для АЧХ:
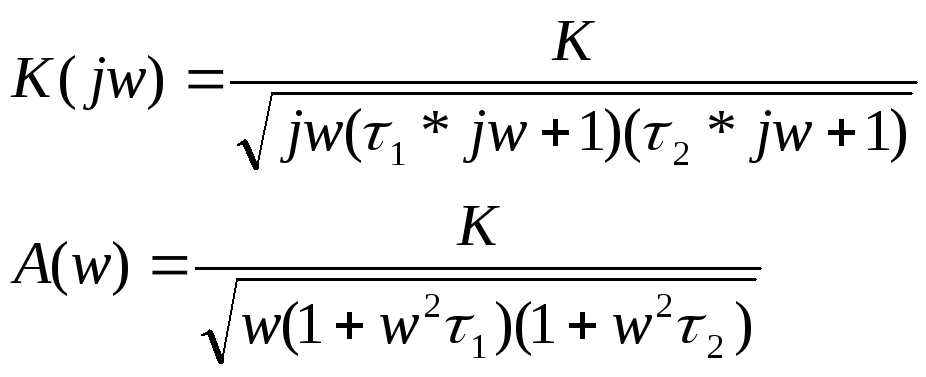
Для ФЧХ:
![]()
-
Построение переходной, импульсной, АЧХ и ФЧХ характеристик в MATLAB.
Построенные характеристики приведены в приложении А
-
Нахождение нулей и полюсов системы
Рассмотрим передаточную функцию для замкнутой системы:
![]() =
=![]()
Так как числитель данной функции является целым числом, это значит, что нулей у данной функции нет.
Найдем полюса в данной системе, для этого найдем корни характеристического уравнения, т.е. знаменателя передаточной функции :
![]() =0
=0
0.0014p![]() +0.15p
+0.15p![]() +p+15=0
+p+15=0
Корни данного уравнения:
![]()
![]()
![]()
Отобразим вычисленные полюса на комплексной плоскости, изображенной на рисунке 1:
Рисунок 2
-
 Определение
устойчивости системы по критериям
Найквиста, Гурвица, Михайлова.
Определение
устойчивости системы по критериям
Найквиста, Гурвица, Михайлова.
5.1 Устойчивость по критерию Найквиста
Для устойчивости замкнутой системы необходимо и достаточно чтобы амплитудно-фазовая характеристика устойчивой разомкнутой системы при изменении ω от 0 до ∞ не охватывала точку с координатами {-1, j0}.
Условия границы устойчивости по критерию Найквиста:
При
K=Kmax
вектор w(j![]() )
= -1+j0,
)
= -1+j0,
w(j![]() )
=
)
=
![]() +j0
;
+j0
;
Выразим отсюда Kmax:
Kmax=
- (![]() )
)
Kmax=
- ( -
![]()
Kmax=
![]()
Сгруппируем члены с мнимой частью:
Kmax=
![]() (1)
(1)
Рассмотрим отдельно мнимую часть, которая равна 0:
![]()
В результате преобразования, получим:
![]() =
=
![]()
Подставим
в
выражение (1)
![]() ,
получим:
,
получим:
Kmax
=
![]()
 Заданный
коэффициент передачи меньше максимального,
значит, данная система устойчива.
Заданный
коэффициент передачи меньше максимального,
значит, данная система устойчива.
