24. Изгиб балки или рамы сопровождается искривлением ее оси. Перемещения балки в сечении z подразделяются на линейные – прогиб у и смещение z и угловые – угол поворота  (рис 6.5).

Осевые перемещения, как правило, несоизмеримо малы, т.е. z<<y и ими пренебрегают.

Искомые перемещения при изгибе у и  могут быть найдены следующими методами:

а) методом начальных параметров (МНП);

б) энергетическим методом.

Особенностью энергетических методов является то, что один расчет, произведенный для

бруса позволяет определить лишь одно перемещение. Поэтому, чтобы построить эпюры

перемещений придется решить ряд задач для нескольких характерных точек бруса.

Энергетические методы применяют обычно тогда, когда необходимо найти перемещение

только в одной-двух точках, например в центре бруса или на его концах. Эти методы особенно удобны при решении статически неопределимых задач. В таких задачах возникает необходимость расчета перемещений для ограниченного числа точек бруса.

Метод Мора является универсальным методом определения любых перемещений

сечений бруса при любой нагрузке. Для каждого из внутренних силовых факторов (ВСФ) Qy,

Mx, Mz, N, My, Qx составляют свой интеграл Мора. Запись интегралов для любого из ВСФ

можно посмотреть в курсе лекций [1]. Общее перемещение есть сумма интегралов Мора для

каждого внутреннего силового фактора.

В пособии рассматривается решение задач определения перемещений только от

внутреннего изгибающего момента Мх. Перемещение от момента рассчитывается как интеграл

Мора:

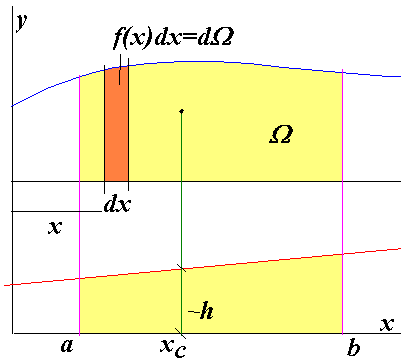
Δ_KF=_i∫_Li((M_F(x)M₁(x)dx)/EI_Z) – интеграл Мора.  Δ_KF – обобщенное перемещение точки К от заданной системы сил. M_F(x) – закон изменения на i^–ом участке изгибающего момента, вызванного действием внешних сил, приложенных к балке.

25. Рассмотрим интеграл, от произведения эпюр моментов, возникающий в формуле Мора,  у х b a  f(x)(kx+m)dx,

где y=f(x) нелинейная эпюра моментов (обычно от действия распределенной нагрузки), аy=kx+m - линейная. Выведем простое правило вычисления этого интеграла. Раскроем скобки и преобразуем  у х b a  f(x)(kx+m)dx = k у х b a  f(x)xdx + m у х b a  f(x)dx.

Второй интеграл это просто площадь нелинейной эпюры  у х b a  f(x)dx = W,

а первый - статический момент  у х b a  xf(x)dx = S

площади нелинейной фигуры относительно оси y. Так как координата центра тяжести имеет вид xc = S/W,

получим  у х b a  f(x)(kx+m)dx = kxcW+ mW = W(kxc+m) = Wh.

Правило Верещагина можно сформулировать так - интеграл от произведения нелинейной эпюры и линейной равен произведению площади нелинейной и ординаты линейной, вычисленной под центром тяжести нелинейной. 

26. Анализ деформированного состояния показывает, что оно обладает свойствами, совершенно аналогичными свойствам напряженного состояния. Среди множества осей, которые могут быть проведены через исследуемую точку, существуют три взаимно перпендикулярные оси, в системе которых угловые деформации отсутствуют. Эти оси называются главными осями деформированного состояния, а линейные деформации в этой системе - главными деформациями. [1]

Анализ деформированного состояния основан на чисто геометрических соотношениях, и поэтому все сказанное остается справедливым для любого однородного тела, независимо от механических свойств материала. [2]

Те́нзор напряже́ний — тензор второго ранга, состоящий из девяти величин, представляющих механические напряжения в произвольной точке нагруженного тела. Эти девять величин записываются в виде таблицы, в которой по главной диагонали стоят нормальные напряжения в трёх взаимно перпендикулярных осях, а в остальных позициях — касательные напряжения, действующие на трёх взаимно перпендикулярных плоскостях.

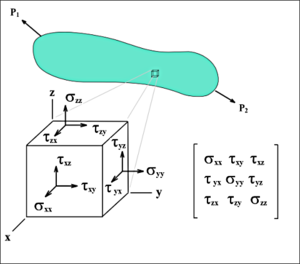
Полный тензор механического напряжения элементарного объёма тела. Буквой σ обозначены нормальные механические напряжения, а касательные буквой τ.

Компоненты тензора напряжений  в декартовой системе координат  (то есть ) вводят следующим образом. Рассматривают бесконечно малый объём тела (сплошной среды) в виде прямоугольного параллелепипеда, грани которого ортогональны координатным осям и имеют площади . На каждой грани  параллелепипеда действуют поверхностные силы. Если обозначить проекции этих сил на оси  как , то компонентами тензора напряжений называют отношение проекций силы к величине площади грани, на которой действует эта сила:

По индексу  здесь суммирования нет. Компоненты , ,, обозначаемые также как , , — это нормальные напряжения, они представляют собой отношение проекции силы  на нормаль к площади рассматриваемой грани :

 и т. д.

Компоненты , ,, обозначаемые также как , , — это касательные напряжения, они представляют собой отношение проекции силы  на касательные направления к площади рассматриваемой грани :

 и т. д.

При отсутствии собственного момента импульса сплошной среды, а также объемных и поверхностных пар тензор напряженийсимметричен (так называемый закон парности касательных напряжений), что является следствием уравнения баланса момента импульса. В частности, тензор напряжений симметричен в классической теории упругости и гидродинамике идеальной и линейно-вязкой жидкостей.

Через произвольную точку тела можно провести бесчисленное множество сечений, на которых возникает напряжение σ и τ, в общем случае отличающиеся друг от друга в зависимости от ориентации площадки. Совокупность напряжений, возникающих на множестве площадок, проведенных через рассматриваемую точку, называют напряженным состоянием в точке.  В окрестности точки В вырезаем элементарные параллелепипед. Поворачивая элементарный параллелепипед вокруг т.В, можно найти такое его положение, при котором на гранях действует только нормальное напряжение, а касательное будет равным 0. Теория упругости доказывает, что для любого тела при любой нагрузке для любой точки можно найти такую ориентацию параллелепипеда, и это будет единственное его положение. Такие площадки, на которых действуют нормальные напряжения, называются главными. Напряжения σ на этих площадках – главные напряжения. Направления σ – главные направления. Р – полное напряжения на рассматриваемой площадке. Если в задаче одно из главных напряжений не равно 0, то такие задачи называются одноосными или линейными. Если не равны 0 два главные напряжения – двухосные или плоские. Если не равны 0 три главные напряжения – трехосные или пространственные.

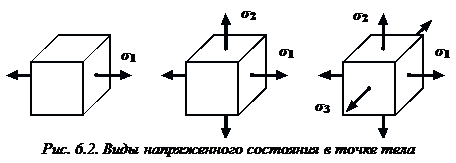
виды напряженного состояния:

линейное (одноосное) напряженное состояние,

плоское (двухосное) напряженное состояние,

объемное (трехосное) напряженное состояние.

С линейным напряженным состоянием мы уже сталкивались при изучении центрального растяжения (сжатия).

 В задачах сопромата часто встречается плоское напряженное состояние. Его характерным признаком является полное отсутствие нормальных и касательных напряжений на двух параллельных гранях параллелепипеда.

Будем полагать, что при плоском напряженном состоянии напряжения не возникают на гранях элементарного параллелепипеда с нормалью x. Тогда вместо объемного параллелепипеда с целью упрощения, мы будем на рисунках показывать проекцию параллелепипеда на плоскость . (штриховкой будем указывать внутреннюю область элемента).

Объемное напряженное состояние в курсе сопротивления материаловпрактически не изучается.

27. При изучении плоского напряженного состояния будем рассматривать только наклонные площадки, которые перпендикулярны граням параллелепипеда, на которых отсутствуют нормальные и касательные напряжения (рис. 6.4).

Положение наклонной площадкиопределяется углом , образующим внешнюю нормаль к этой площадке с осью z. Угол  положителен, если отсчитывается против хода часовой стрелки.

Нормальные и касательные напряжения на наклонной площадке, проходящей через точку К, определяются по формулам:

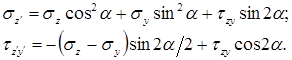
Из формул нормальных и касательных напряжений на наклонных площадках, проходящих через рассматриваемую точку, видно: напряжения в наклонных площадках являются непрерывными функциями угла и могут иметь экстремальные значения: максимумы и минимумы.

Найдем угол наклона площадки , при котором нормальное напряжение принимает экстремальное значение.

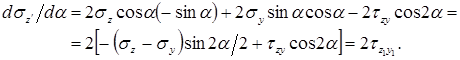
Приравняем формулу к нулю. Получим формулу экстремального значения угла наклона площадки:

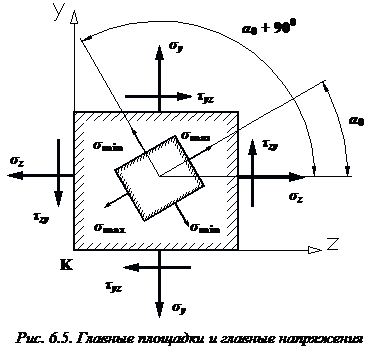 Найдем углы и , определяющие положение двух взаимно перпендикулярных площадок, на которых возникают экстремальные нормальные напряжения и в рассматриваемой точке К (рис. 6.5).

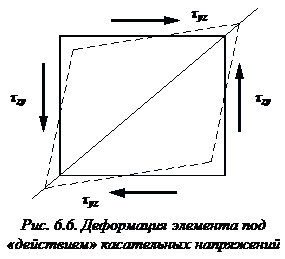
Максимальное нормальное напряжение всегда направлено в сторону, где сходятся касательные напряжения . (см. рис. 6.6.)

Касательные напряжения «создают» дополнительное удлинение одной из диагоналей.