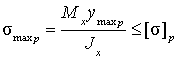10. Упругими называют деформации, исчезающие после снятия вызвавшей их нагрузки.

Остаточные (пластические) – часть полных деформаций не исчезающая после разгружения элемента.

Хрупкость — свойство материала разрушаться без образования заметных остаточных деформаций. Является противоположным свойству пластичности. Материалы, обладающие этим свойством, называются хрупкими. Для таких материалов удлинение при разрыве не превышает 2…5 %, а в ряде случаев измеряется долями процента. К хрупким материалам относятся чугун, высокоуглеродистая инструментальная сталь, стекло, кирпич, камни и др. Диаграмма растяжения хрупких материалов не имеетплощадки текучести и зоны упрочнения.

 Пластические при статических испытаниях до разрушения получают значительные остаточные деформации. Примеры пластичных материалов большинство металлов, металл

Пластичность - свойство твердых материалов изменять без разрушения форму и размеры под влиянием нагрузки или внутренних напряжений, устойчиво сохраняя образовавшуюся форму после прекращения этого влияния.ических сплавов, пластмасс.

11. Пластичный материал

Для пластичного материала [s]_r=[s]_c. В данном случае рационально использовать симметричные профили (при этом s_maxr=s_maxс).

Экономичными являются профили с уменьшенной металлоемкостью в области нейтральной линии, такие как двутавр и швеллер. Показателем экономичности является удельный момент сопротивления . Чем выше величина w_x, тем профиль более экономичен.

Для круга	wx=0,141.
Для кольца d/D=0,7	wx=0,294.
Для двутавра №10	wx=0,955.
Для двутавра №20	wx=1,33

Сечение следует располагать таким образом, чтобы силовой фактор действовал в плоскости максимальной жесткости.

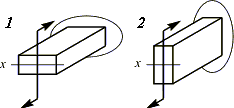
Случай 2 более выгодный, т.к.

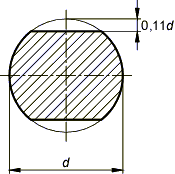
Простое увеличение размеров сечения не всегда эффективно. Так, если у круглого сечения вырезать сегменты высотой в пределах 0,11d, получится более экономичный профиль, чем сплошной круг.

Хрупкий материал

Для хрупкого материала , поэтому в данном случае целесообразно использовать несимметричные относительно нейтральной линии профили, например, тавровый:

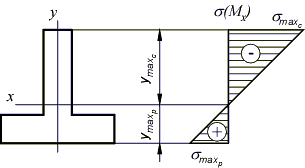
Размеры поперечного сечения должны удовлетворять двум условиям:

(5.6)

 

(5.7)

Из подобия треугольников эпюры σ(М_х) следует, что .

Если 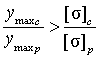, опасными являются сжатые волокна и расчет на прочность следует вести по формуле (5.6).

Если 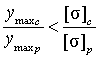, опасными являются растянутые волокна и расчет на прочность следует вести по формуле (5.7)

[σ]=σ₀/ n где σ₀-опасное напряжение (σ_Т. – для деталей из пластичного материала, σ_ВР.- для деталей из хрупкого материала) n- коэффициент запаса прочности, показывающий, во сколько раз допускаемое напряжение меньше опасного. Выбор величины коэффициента запаса прочности зависит от состояния материала (хруп- кое или пластичное), характера приложения нагрузки (статическая, динамическая, повторно- переменная) и некоторых общих факторов.

12. Таким образом, моментом (статическим моментом) площади фигуры относительно оси называется произведение площади на расстояние от ее центра тяжести до оси. Осевой момент инерции фигуры - это интеграл произведений элементарных площадей на квадраты их расстояний до рассматриваемой оси. Формулы осевого момента инерции произвольной фигуры (см. рис. 4.1) относительно осей x и y:

Полярный момент инерции фигуры относительно данной точки (полюса) - это интеграл произведений элементарных площадей на квадраты их расстояний до полюса:

Если через полюс проведена система взаимно перпендикулярных осей x и y, то , и формула полярного момента инерции равна сумме осевых моментов инерции относительно осей x и y:

Из формул осевых и полярного моментов инерции видно: значения осевых и полярного моментов инерции всегда положительны, так как координаты и расстояние возведены в квадрат.

Центробежный момент инерции фигуры - это интеграл произведений элементарных площадей на их расстояния до осей x и y:

Моменты инерции измеряются в единицах длины в четвертой степени (как правило, см4).

Понятие момента инерции поперечного сечения ввел в 1834 г. французский ученый Н. Перси.

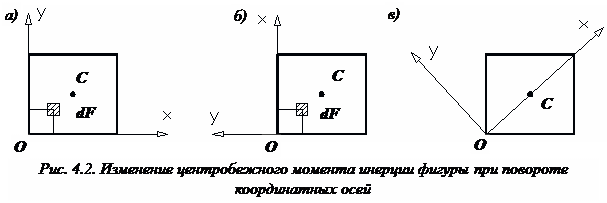
13. Пусть две взаимно перпендикулярные оси x и y проходят через центр тяжести C поперечного сечения стержня. Проведем другие оси координат и , параллельные осям x и y. Обозначим a и b координаты центра тяжести С в новых осях и (рис. 4.3, а).

Тогда формулы осевых и центробежных моментов инерции фигуры относительно параллельных осей и :

Первые слагаемые в формулах осевых и центробежных моментов инерции фигуры относительно параллельных осей названы собственными моментами инерции. Вторые (подчеркнутые) слагаемые называются переноснымимоментами инерции.

Отметим, что координаты a и b необходимо подставлять в формулы моментов инерции фигуры относительно параллельных осей с учетом их знаков, что является крайне важным для третьей из приведенных формул.

14.
14.

Главные оси имеют важное практическое применение. Каким свойством обладают главные оси?

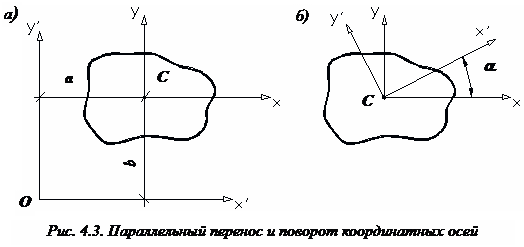
Центробежный момент инерции может быть положительным, отрицательным, а также равным нулю в зависимости от положения координатных осей. Рассмотрим квадрат (рис. 4.2, а).

Центробежный момент инерции квадрата () относительно осей положителен, поскольку координаты всех элементов площади положительны. При повороте осей вокруг начала координат на угол 900 (рис. 4.2 б) знак центробежного момента инерции становится отрицательным, так как в этом случае координаты x всех элементарных площадей положительны, а координаты y – отрицательны.

Можно найти положение двух взаимно перпендикулярных осей, при котором . Такие оси называются главными осями. Главные оси для квадрата изображены на (рис. 4.2, в).

Если фигура имеет ось симметрии, то эта ось является одной из главных осей (другая ей перпендикулярна).

Главные оси, проходящие через центр тяжести поперечного сечения стержня, называются главными центральными осями.

Пусть нам известны собственные моменты инерции , и относительно двух взаимно перпендикулярных осей x и y, проходящих через центр тяжести C поперечного сечения стержня. Проведем через точку C другие оси и , повернутые относительно осей x и y на угол (рис. 4.3, б). Будем считать этот угол положительным при повороте осей координат против хода часовой стрелки.

Моменты инерции поперечного сечения при повороте осей координатопределяются по формулам:

;

.

Из формул моментов инерции при повороте осей координат видно, что сумма собственных осевых моментов инерции не изменяется при повороте координатных осей: 

Две взаимно перпендикулярные оси, проходящие через центр тяжести фигуры, относительно которых центробежный момент инерции равен нулю, называются главными центральными осями инерции. Тогда из третьей формулы моментов инерции при повороте осей координат легко можно определить направление этих осей:

Из полученного выражения найдем два значения угла , которые отличаются друг от друга на угол , которые определяют положение двух главных центральных осей.

15. Моменты сопротивления простых фигур (табл. 4.1):

·     прямоугольник ;

·   треугольник   ;

·     круг  ;

·     кольцо   .

16. Чистый сдвиг – это такой вид деформации при котором в поперечном сечении детали возникает только поперечная сила Q. Чистый сдвиг – частный случай плоского напряженного состояния, при ко-

тором по граням прямоугольного элемента действуют только касательные

напряжения.

При чистом сдвиге главные напряжения одинаковы по величине,

противоположны по знаку (σ1=–σ3=τxy) и направлены под углом 45о

к оси стержня (третья главная площадка элемента совпадает с ненагруженной фа-

садной гранью элемента, следовательно σ2=0).  

Принимая во внимание, что касательные напряжения распределены равномерно по поперечному сечению А, их значение определяется соотношением:

 

.                                       (2.29) 

 

Экспериментально установлено, что в пределах упругих деформаций величина касательных напряжений пропорциональна относительному сдвигу(закон Гука при сдвиге):

 

,                                                (2.30)

 

где G – модуль упругости при сдвиге (модуль упругости второго рода).

17. Кручение – вид деформации при котором в сечении детали возникает только крутящий момент Т. Крутящий момент, возникающий в поперечном сечении стержня, определяетсяметодом сечений. Крутящий момент равен алгебраической сумме скручивающихмоментов, приложенных к любой из частей стержня. Эпюра крутящих моментов – это график, показывающий изменения крутящего момента по длине вала .

ПРАВИЛО ЗНАКОВ ДЛЯ ЭПЮРЫ КРУТЯЩИХ МОМЕНТОВ

При построении эпюры крутящих моментов используется правило знаков:

Скручивающий момент, вращающий рассматриваемую часть стержня против ходачасовой стрелки при взгляде на поперечное сечение, вызывает в этом сечении положительный крутящий момент, направленный по ходу часовой стрелки, противодействуя скручивающему моменту.

18. Вращающийся стержень, работающий на кручение называют валом. Стержень, используемый как упругий элемент, который работает на скручивание, называется торсионом. Касательные напряжения , возникающие в условиях кручения, определяются по формуле:

,

где r — расстояние от оси кручения.

Очевидно, что касательные напряжения достигают наибольшего значения на поверхности вала при  и при максимальном крутящем моменте , то есть

,

где W_p — полярный момент сопротивления.

Гипотезы при кручении

1. Выполняется гипотеза плоских сечений: поперечное сечение бруса, плоское и перпендикулярное продольной оси, после деформациии остается плоским и перпендикулярным продольной оси.

2.  Радиус, проведенный из центра поперечного сечения бруса, после деформации остается прямой линией (не искривляется).

3. Расстояние между поперечными сечениями после деформации не меняется. Ось бруса не искривляется, диаметры поперечных сечений не меняются.

Закон распределения по сечению - напряжения распределены вдоль радиуса поперечного сечения по линейному закону: в центре сечения они равны нулю (рис. 6.8, а), а в точках наружного контура достигают наибольшего значения .

условие прочности при кручении в таком виде:

.

19.  деформация кручения: одно поперечное сечение повернется на некоторый угол относительно другого (расстояние между сечениями останется прежним, если угол поворота мал). В поперечных сечениях стержня, при кручении, возникнет только одновнутреннее усилие – крутящий момент ().

Угол закручивания цилиндрического стержня в границах упругих деформаций под действием момента T может быть определён из уравнения закона Гука для случая кручения

где:

 — геометрический полярный момент инерции;

 — длина стержня;

G — модуль сдвига.

Отношение угла закручивания φ к длине  называют относительным углом закручивания

Условие жесткости требует, чтобы максимальный относительный угол закручивания , был меньше или в предельном случае равен допускаемому углу закручивания единицы длины вала, т.е.

 .   

20. Общие понятия о деформации изгиба.

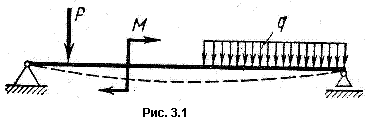
Весьма часто стержни подвергаются действию поперечной нагрузки или внешних пар (рис. 3.1).

При этом в поперечных сечениях стержня возникают изгибающие моменты, т.е. внутренние моменты, плоскость действия которых перпендикулярна плоскости поперечного сечения стержня.

При действии такой нагрузки ось стержня искривляется.

Указанный вид нагружения называют изгибом. Стержни, работающие в основном на изгиб, обычно называют балками. Изгиб называют чистым, если изгибающий момент является единственным внутренним усилием, возникающим в поперечном сечении стержня.

Чаще, однако, в поперечных сечениях стержня наряду с изгибающими моментами возникают тоже и поперечные силы. Такой изгиб называют поперечным.

Если плоскость действия изгибающего момента (силовая плоскость) проходит через одну из главных центральных осей поперечного сечения стержня, изгиб называют простым или плоским (применяется также название: прямой изгиб).

Если плоскость действия изгибающего момента в сечении не совпадает ни с одной из главных осей сечения, изгиб называют косым.

Далее будет показано, что при плоском изгибе ось балки и после деформации остается в плоскости внешних сил - силовой плоскости. При косом изгибе плоскость деформации не совпадает с силовой плоскостью.

Дифференциальные зависимости при изгибе; -первая диф. зависимость: q=dQ(x)/dx. Первая производная от перерезывающей силы по длине балки равна погонной нагрузке -вторая диф. зависимость: Q(x)=dM(x)/dx.Величина Q(х)=-а tg угла наклона на эпюры М ( касательной эпюры) к оси эпюры -третья диф. зависимость q=d² M(x)/dx² Когда на рассматриваемом участке действует, кроме того, расспределенный момент интенсивностью m, H·м/м, формула принимает следующий вид; dM/dx=Q+m

21. Эпюры поперечных сил и изгибающих моментов нужны для наглядного представления о характере изменения внутренних силовых факторов по длине балки. Также эпюры поперечных сил и изгибающих моментов строят с целью определения опасных сечений, в которых возникают наибольшие касательные и нормальные напряжения.

Поперечная сила в рассматриваемом поперечном сечении численно равна алгебраической сумме всех внешних сил (активных и реактивных), действующих на отбрасываемую часть балки при использовании метода сечений.

Изгибающий момент в рассматриваемом поперечном сечении численно равен алгебраической сумме моментов всех усилий, приложенных к отбрасываемой части балки относительно горизонтальной оси, проходящей через центр тяжестисечения.

Если на участке балки отсутствует распределенная нагрузка (), то эпюра поперечных сил на этом участке представляет собой прямую, параллельную оси балки (рис. 7.6). По дифференциальной зависимости распределенной нагрузки и поперечной силы: поскольку , то и . Следовательно, .

Эпюра изгибающих моментов на участке, где , – прямая линия. Причем, если , то прямая идет вверх, а если , прямая идет вниз. Если , то изгибающий момент постоянен, поскольку .

ПРАВИЛО ПОСТРОЕНИЕ ЭПЮР – СКАЧКИ И ИЗЛОМЫ

Под сосредоточенной силой (P) на эпюре поперечных сил (рис. 7.6, а) имеется скачок на величину этой силы и по ее направлению, а на эпюре изгибающих моментов – излом, угол которого направлен навстречу нагрузке.

ПРАВИЛО ПОСТРОЕНИЕ ЭПЮР – ПРИСУТСТВУЕТ РАСПРЕДЕЛЕННАЯ НАГРУЗКА

Если на участке балки имеется равномерно распределенная нагрузка: эпюра поперечных сил представляет собой наклонную прямую (рис. 7.6, б), идущую вниз, если нагрузка направлена вниз (и наоборот). Эпюра на этом участке, согласно третьей формуле дифференциальных зависимостей, изменяется по квадратичной параболе, выпуклость которой направлена навстречу нагрузке.

ПРАВИЛО ПОСТРОЕНИЕ ЭПЮР – ЭКСТРЕМУМ

Если эпюра поперечной силы проходит через нулевое значение, то в этом сечении балки на эпюре изгибающих моментов имеется экстремум (последнее вытекает из дифференциальной зависимости ). В точках, соответствующих началу и концу участка, в пределах которого действует распределенная нагрузка, параболическая и прямолинейная части эпюры переходят одна в другую плавно (без излома).

ПРАВИЛО ПОСТРОЕНИЕ ЭПЮР – ВНЕШНИЙ МОМЕНТ

Сосредоточенный внешний момент M (рис. 7.6, в) никак не отражается на эпюре . На эпюре в месте приложения этого момента имеется скачок на его величину.

Заметим, что построение эпюр поперечных сил и изгибающих моментов ввел в практику расчета балок на изгиб французский ученый Жан Антуан Шарль Бресс (1822 – 1883 гг.) в 1859 г.

правила знаков:

1. Поперечная сила положительна, если она стремится сдвинуть левую часть балки вверх относительно правой или правую часть балки вниз относительно левой, как бы вращая обе части балки по часовой стрелке (рис. 19);

2. Изгибающий момент положителен, если он изгибает балку выпуклостью вниз, и отрицателен, если выпуклостью вверх.

22. При изгибе балки одни слои ее растягиваются, другие сжимаются. Между ними находится нейтральный слой, который лишь искривляется, не изменяя при этом своей длины. Линия пересечения нейтрального слоя с плоскостью поперечного сечения совпадает со второй главной осью инерции и называется нейтральной линией (нейтральной осью).

От действия изгибающего момента в поперечных сечениях балки возникают нормальные напряжения, определяемые по формуле

где  М – изгибающий момент в рассматриваемом сечении;

I – момент инерции поперечного сечения балки относительно нейтральной оси;

у – расстояние от нейтральной оси до точки, в которой определяются напряжения.

Как видно из формулы (8.1), нормальные напряжения в сечении балки по ее высоте линейны, достигая максимального значения в наиболее удаленных точках от нейтрального слоя.

где W – момент сопротивления поперечного сечения балки относитель¬но нейтральной оси.

Гипотезу плоских сечений при изгибе можно объяснить на примере: нанесем на боковой поверхности недеформированной балки сетку, состоящую из продольных и поперечных (перпендикулярных к оси) прямых линий. В результате изгиба балки продольные линии примут криволинейное очертание, а поперечные практически останутся прямыми и перпендикулярными к изогнутой оси балки.

Формулировка гипотезы плоских сечения: поперечные сечения, плоские и перпендикулярные к оси балки до деформации, остаются плоскими и перпендикулярными к изогнутой оси после ее деформации.

Это обстоятельство свидетельствует: при изгибе выполняется гипотеза плоских сечений, как при растяжении и кручении

слой, в котором нормальные напряжения о равны нулю; такой слой называют нейтральным слоем (НС). 

При изгибе балки одни слои ее растягиваются, другие сжимаются. Между ними находится нейтральный слой, который лишь искривляется, не изменяя при этом своей длины. Линия пересечения нейтрального слоя с плоскостью поперечного сечения совпадает со второй главной осью инерции и называется нейтральной линией (нейтральной осью).

От действия изгибающего момента в поперечных сечениях балки возникают нормальные напряжения, определяемые по формуле

где  М – изгибающий момент в рассматриваемом сечении;

I – момент инерции поперечного сечения балки относительно нейтральной оси;

у – расстояние от нейтральной оси до точки, в которой определяются напряжения.

Как видно из формулы (8.1), нормальные напряжения в сечении балки по ее высоте линейны, достигая максимального значения в наиболее удаленных точках от нейтрального слоя.

где W – момент сопротивления поперечного сечения балки относитель¬но нейтральной оси.

23. Условия прочности при изгибе |мах.σ_сжат|≤[σ_сжат] |махσ_растяж|≤[σ_растяж]

при изгибе целого бруса высотой 2h между частями бруса, разделенными продольными слоями, возникает взаимодействие, в результате которого и возникают касательные напряжения (рис. 1, в).

Касательное напряжение в любой точке поперечного сечения (рис. 2) определяется, как и парное напряжение, возникающее в продольном сечении, по формуле Журавского;

где - поперечная сила в рассматриваемом сечении;  - статический момент относительно нейтральной оси поперечного сечения той его части, которая расположена по одну сторону от прямой KL, проведенной параллельно нейтральной оси через исследуемую точку; b - ширина поперечного сечения на уровне исследуемой точки; - момент инерции всего сечения относительно нейтральной оси.

ледовательно, искривления поперечных сечений не сказываются на законе распределения нормальных напряжений и их значений. В балке прямоугольного и круглого сечений максимальные касательные напряжения возникают в тех точках, где нормальные напряжения равны нулю (на нейтральной оси), и, наоборот, в крайних точках сечения, где нормальные напряжения максимальны, касательные напряжения равны нулю. Поэтому за опасные можно принять точки, наиболее удаленные от нейтральной оси, что подтверждается практикой эксплуатации балок, работающих на изгиб. Однако в случае тонкостенных профилей (например, двутавра) необходимо проверить прочность балки и в точках, где полка сочленяется со стенкой, поскольку здесь возникают значительные как нормальные, так и касательные напряжения.