
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОУ ВПО ¾НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ¿
Т.И.Семенко, О.В.Скворцова
ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ ПО МАТЕМАТИЧЕСКОМУ АНАЛИЗУ
Множества. Функции. Предел и непрерывность
Утверждено Редакционно-издательским советом НГПУ в качестве учебно-методического пособия
НОВОСИБИРСК 2010
ÓÄÊ 517(075.8) ÁÁÊ 22.161ÿ73 1 Ñ301
Рецензенты:
кандидат физико-математических наук, доцент Омского государственного университета
Н.С.Зиндинова;
кандидат физико-математических наук, профессор Новосибирского государственного педагогического университета
Г.Я.Ярахмедов
Семенко, Т.И.
С301 Индивидуальные задания по математическому анализу. Множества. Функции. Предел и непрерывность: учеб. - метод. пособие/Т.И.Семенко, О.В.Скворцова. Новосибирск: Изд. НГПУ, 2010. 140 с.
Сборник содержит индивидуальные задания по темам "Множества" , "Функции" , "Предел и непрерывность" , "Вычисление пределов" , снабженные указаниями к решению задач, а также подробными решениями задач одного из вариантов.
Пособие адресовано студентам математических факультетов педагогических университетов.
ÓÄÊ 517(075.8) ÁÁÊ 22.161ÿ73 1
c Семенко Т.И., Скворцова О.В, 2010
c ГОУ ВПО "Новосибирский государственный педагогический университет" , 2010
Введение
В связи с введением новых государственных образовательных стандартов значительная часть работы по освоению учебного материала переносится на самостоятельные, внеаудиторные занятия студентов.
Настоящее учебное пособие, адресованное студентам и преподавателям математических факультетов педагогических университетов, может быть полезно при организации самостоятельной работы студентов, изучающих вводный курс математического анализа.
Книга состоит из четырех разделов, в каждом из которых содержится по 16 вариантов индивидуальных заданий по одной из тем: "Множества" , "Функции" , "Предел и непрерывность" , "Вычисление пределов" . Каждый раздел сопровождается указаниями к решению задач по соответствующей теме и подробными решениями задач одного из вариантов (нулевого варианта). Все варианты задания по теме "Вычисление пределов" снабжены ответами. Задачи, отмеченные знаком *, не являются обязательными для выполнения студентами.
Сборник составлен с учетом опыта организации самостоятельной работы студентов 1-го курса математического факультета преподавателями кафедры математического анализа Новосибирского государственного педагогического университета. Ими же составлена большая часть вошедших в данное пособие задач.
Пособие предназначено в первую очередь для студентов оч- ного отделения математического факультета, однако может быть рекомендовано и студентам - заочникам.
3

1. Индивидуальное задание по теме "Множества"
Вариант •0
1. Найдите все элементы числовых множеств A; B; A B; A ∩B;
A \ B; B \ A; A∆B; åñëè |
|
|
|
|
|
|
|
|
|
|
| |x| < (x + 1) |
2 |
; |
||||||||
à) A = {x [− =2; =2] | tg 3x > 1} ; B = x R |
|
||||||||||||||||||||
á) A = x |
|
N |
|
20 |
|
N ; B = x |
|
N{ |
x2 |
|
14x + 33 |
|
0 : |
} |
|||||||
{ |
|
|
| |
|
|
|
} |
|
|
| |
|
|
− |
|
≤ |
} |
|
|
|||
|
x |
|
|
B) |
(A C). |
|
|
||||||||||||||
2*. Докажите равенство |
A (B |
C) = (A |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
{ |
|
|
|
|
|
|
|
|
\ |
|
|
|
||
3*. Докажите, что если A \B = A, òî B \A: ∩ |
|
|
|
|
|||||||||||||||||
4. Докажите иррациональность числа |
√ |
2 |
: |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
5. Докажите иррациональность числа |
√3 r= ; ãäå I; à |
|
|
||||||||||||||||||
r Q \ {0}: |
|
|
|
|
|
|
|
|
|
|
|||||||||||
√
6*. Докажите неравенство a2 + b2 ≤ |a| + |b|, справедливое для всех чисел a è b.
7.Решите уравнение |x − 2| = |x2 − 5x + 6|:
8.Решите неравенство 4|x − 3| > |x2 + 2x − 3|:
9*. Докажите методом математической индукции справедливое для всех натуральных чисел равенство
|
1 |
|
+ |
|
1 |
+ : : : + |
|
1 |
|
= |
1 |
· |
3n |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
5 |
· |
8 |
8 |
· |
11 |
(3n + 2) |
· |
(3n + 5) |
15 |
3n + 5 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
10. Выясните, является ли множество A ограниченым снизу, огра-
ниченным сверху, ограниченным, и найдите его нижнюю и верхнюю грани, а также наименьший и наибольший элементы (в слу- чае их существования), если
a) A = {x R | √ |
x |
2 |
|
≥ 2} |
; á) A = {x I | 24 x |
2 |
|
1 |
} ; |
|||
|
− |
|
|
≤ |
|
|||||||
3 |
x |
|
16 |
|||||||||
â) A = { |
2 |
|
|
|
− |
} : |
|
|
|
|
|
|
4n − |
3 |
| n N |
|
|
|
|
|
|||||
5n2 |
|
|
|
|
|
|
||||||
4

Вариант •1
1. Найдите все элементы числовых множеств A; B; A B; A ∩B;
A \ B; B \ A; A∆B; åñëè |
|
1 |
{ |
|
|
|
|
|
|
} |
|
|||
20 |
|
|
|
|
|
|
|
|
|
|||||
à) A = {x N | |
|
N |
} ; B = x N | 3x2 − 32x − 8 6 0 ; |
|
||||||||||
x |
|
|||||||||||||
á) A = {x [− ; ] | cos 2x > |
|
} ; B = |
|
x R | x2 − x − 12 < 0 |
: |
|||||||||
2 |
A |
|||||||||||||
2*. Докажите равенство |
A \ (B \ C) = ( |
\ |
B) |
|
(A |
∩ |
C): |
} |
||||||
|
|
|
{ |
|
|
|
||||||||
3*. Докажите, что если A B; òî A ∩ B = A: |
|||
4. Докажите иррациональность числа |
√ |
8 |
: |
5. Докажите иррациональность числа |
· r; ãäå I; à r Q : |
||
6*. Докажите, что для любого числа x справедливы неравенства
−|x| 6 x 6 |x|: |
|
|
x + |
3 |
|
x + 1 < 2: |
|||||||
8. |
Решите неравенство |
|
|||||||||||
7. |
Решите уравнение |
|
x |
− 1 |
|
= |
x |
− 1 |
: |
|
|
||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
− | |
|
|
|
|
| |
индукции справедливое |
|||
9*. Докажите методом |математической| |
|
|
|
|
|||||||||
|
|
x + 1 |
|
|
x + 1 |
|
|
||||||
для всех натуральных чисел равенство |
|
||||||||||||
|
12 + 22 + 32 + : : : + n2 = |
1 |
n · |
(n + 1) · (2n + 1) : |
|||||||||
|
|
|
|||||||||||
|
|
6 |
|||||||||||
10. Выясните, является ли множество A ограниченым снизу, огра-
ниченным сверху, ограниченным, и найдите его нижнюю и верхнюю грани, а также наименьший и наибольший элементы (в слу- чае их существования), если
a) A = {x Z | |
x |
3 |
|
< 0} ; á) A = {x Q | |
x |
3 |
≤ 0} ; |
||||
|
− |
|
|
− |
|||||||
2x 1 |
2x 1 |
||||||||||
2 |
|
|
|
− |
|
|
|
− |
|||
â) A = { |
n |
| n N |
} : |
|
|
|
|
||||
n2 + 2 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
Вариант •2 |
|
|
|
|
1. Найдите все элементы числовых множеств A; B; A B; A ∩B; |
|||||||||||
A \ B; B \ A; A∆B; åñëè |
|
|
|
|
|
||||||
à) A = {x N | |
|
x |
N; x ≤ 20} ; B = {x N | |
|
x |
N; x ≤ 20} ; |
|||||
4 |
6 |
||||||||||
5

á) A = {x R | |
x |
|
≥ 0} ; B = x R | x3 + x2 − x − 1 < 0 : |
|||||||
x2 |
1 |
|||||||||
|
− |
|
|
) = (A |
\ |
B) |
|
(A |
\ |
C). |
2*. Докажите равенство |
||||||||||
|
|
|
|
A \ (B ∩ C{ |
|
|
} |
|||
3*. Докажите, что если A C è B C; òî A B C:
4.Докажите иррациональность числа 2 log3 5:
5.Докажите иррациональность числа + r; ãäå I; à r Q:
6*. Докажите, что для любых чисел a; b справедливо неравенство |a + b| ≤ |a| + |b|:
7.Решите уравнение |x − 4; 2| · (x − 4; 2) = −1:
8.Решите неравенство |x| > |x + 1|:
9*. Докажите методом математической индукции справедливое для всех натуральных чисел равенство
13 + 23 + 33 + : : : + n3 = 14 · n2 · (n + 1)2 :
10. Выясните, является ли множество A ограниченым снизу, огра-
ниченным сверху, ограниченным, и найдите его нижнюю и верхнюю грани, а также наименьший и наибольший элементы (в слу- чае их существования), если
a) A = {x Z | |
x |
3 |
< 0} ; á) A = {x I | |
2x |
3 |
≤ 0} ; |
|||
2 − |
x |
|
− |
||||||
x 1 |
|
1 |
|||||||
â) A = |
|
|
− |
: |
|
|
− |
|
|
{n | n N} |
|
|
|
|
|
||||
|
3 |
|
|
|
|
|
|
|
|
Вариант •3
1. Найдите все элементы числовых множеств A; B; A B; A ∩B;
A \ B; B \ A; A∆B; åñëè |
|
|
|
|
|
|
|
|
|
|
x |
2 |
− x − 2 |
|
|
||||||||||||
à) A = x |
|
R |
| |
x3 |
− |
3x2 + 2x |
≤ |
0 ; B = x |
|
R |
| |
|
≥ |
0 ; |
|||||||||||||
|
|
||||||||||||||||||||||||||
2*. |
|
{ |
|
|
|
|
|
} |
{ |
|
|
|
|
x − 1 |
|
} |
|||||||||||
|
|
|
|
|
|
x |
|
|
} |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|||||
|
|
{ |
|
|
|
|
|
|
|
; B = {x Z | |
x + 5 |
< 0} : |
|||||||||||||||
á) A = |
x Z | cos |
|
|
= 1; |x| ≤ 10 |
|
||||||||||||||||||||||
|
3 |
x − 4 |
|||||||||||||||||||||||||
|
Докажите равенство |
(A \ B) \ C = (A \ C) \ |
(B \ C) |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
3*. Докажите, что если C A è C B; òî C A ∩ B: |
|
|
|
|
|||||||||||||||||||||||
4. Докажите иррациональность числа √ |
2 |
+ |
√ |
3 |
: |
|
|
|
|
|
|
|
|
||||||||||||||
5. Докажите иррациональность числа r − ; ãäå I; à r Q:
6

6*. Докажите, что для любых чисел a; b справедливо равенство
|a − b| = |b − a|:
7.Решите уравнение | tg x| = tg x:
8.Решите неравенство |x − 3| + |x + 3| > 8:
9*. Докажите методом математической индукции справедливое для всех натуральных чисел равенство
1·2·3+2·3·4+: : :+n·(n+1)·(n+2) = 14 ·n·(n+1)·(n+2)·(n+3) :
10. Выясните, является ли множество A ограниченым снизу, огра-
ниченным сверху, ограниченным, и найдите его нижнюю и верхнюю грани, а также наименьший и наибольший элементы (в слу- чае их существования), если
a) A = {x R |
|
x |
|
4 |
< 1} ; á) A = {x Q |
|
|
|
|
x |
4 |
≤ 1} ; |
|
||||||||||||||
| |
− |
|
| |
|
− |
|
|
||||||||||||||||||||
2x |
3 |
2x |
3 |
|
|||||||||||||||||||||||
â) A = { |
|
2 |
+ 1 |
|
|
|
− |
} : |
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
||||
n |
|
| |
|
n N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
Вариант •4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1. Найдите все элементы числовых множеств A; B; A B; A ∩B; |
|||||||||||||||||||||||||||
A \ B; B \ A; A∆B; åñëè |
|
|
|
|
|
|
|
|
|
x |
2 |
− 8x − 12 |
|
|
|||||||||||||
à) A = |
{ |
x |
|
[0; 2 ] |
| |
sin x < 0 |
} |
; B = |
x |
|
R |
| |
|
|
|
≥ |
0 ; |
||||||||||
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
{ |
|
|
|
|
|
x − 4 |
|
} |
|||||||||
á) A = {x Z |
| |
2 |
Z} ; B = {x Z | |
|
x + 3 |
≤ 0} : |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||
x |
|
x + 1 |
|
|
|
|
|||||||||||||||||||||
2*. Докажите включение (A B) \ C (A \ C) B. 3*. Докажите, что если C A ∩ B, òî C A è C B:
4.Докажите иррациональность числа log3 4:
5.Докажите иррациональность числа r= , ãäå I; à r Q:
6*. Докажите, что равенство |a + b| = |a| + |b| справедливо тогда и только тогда, когда a · b ≥ 0.
7.Решите уравнение |x2 + 4x − 21| = −(x2 + 4x − 21):
8.Решите неравенство ||x + 1| − |x − 1|| < 1:
9*. Докажите методом математической индукции справедливое для всех натуральных чисел равенство 1 + 3 + : : : + (2n −1) = n2:
7
10. Выясните, является ли множество A ограниченым снизу, огра-
ниченным сверху, ограниченным, и найдите его нижнюю и верхнюю грани, а также наименьший и наибольший элементы (в слу- чае их существования), если
|
|
|
|
|
3x − 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2√ |
|
|
|
|
|
||||||||||||
a) A = x |
|
R |
| |
|
≥ − |
1 ; á) A = x |
|
Q |
| |
3 |
− |
x < 1 ; |
||||||||||||||||||||||||
|
|
{ |
|
|
|
|
x + 1 |
|
} |
|
{ |
|
|
|
|
|
|
|
|
|
|
} |
||||||||||||||
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
â) A = {1 + |
|
|
+ |
|
+ : : : + |
|
| n N} : |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
2 |
22 |
2n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Вариант •5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1. Найдите все элементы числовых множеств A; B; A B; A ∩B; |
||||||||||||||||||||||||||||||||||||
A \ B; B \ A; A∆B; åñëè |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x − 3 |
|
|
|
|
|
|||||||||||||||
à) A = |
x |
|
[0; ] |
| |
tg2 |
2x < 3 |
|
; B = |
x |
|
R |
| |
|
|
≤ |
0 |
|
; |
||||||||||||||||||
|
|
{ |
|
|
|
|
|
|
|
|
|
} |
{ |
|
|
|
|
|
|
x + 1 |
} |
|||||||||||||||
|
|
|
|
|
|
|
|
x2 + x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
− |
2 |
|
|
|
|||||||
á) A = x |
|
Z |
|
| |
− |
10 |
≤ |
0 ; B = x |
|
|
Z |
| |
|
|
≤ |
0 : |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
{ |
|
|
|
x + 5 |
} |
||||||||||||||||||
2*. |
Докажите равенство |
(A |
|
|
B)} A = A |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
{ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∩ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3*. Докажите, что если A B = C, òî A C è B C: |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. Докажите иррациональность числа √ |
20: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
ãäå |
I; |
à |
|
r Q: |
||||||||||||||||||||||||||||
5. Докажите иррациональность числа |
r + ; |
|
|
|
|
|
||||||||||||||||||||||||||||||
6*. Докажите справедливость равенства |a·b| = |a|·|b| для любых
чисел a è b. |
√ |
|
|
|
|
|
|
|
||
8. |
Решите |
|
x |
(x |
|
2 |
1) < 20 : |
|||
7. |
Решите уравнение |
|
(x − 5) |
|
= −x |
1 |
|
|||
|
|
|
|
|
|
|
|
|
+ 2: |
|
|
|
неравенство |
|
|
|
|
|
|
|
|
|
|
|
| · |
|
− |
| |
|
|
||
|
|
|
|
|
|
|||||
9*. Докажите методом математической индукции справедливое для всех натуральных чисел равенство
1 · 2 + 2 · 5 + : : : + n · (3n − 1) = n2 · (n + 1) :
10. Выясните, является ли множество A ограниченым снизу, огра-
ниченным сверху, ограниченным, и найдите его нижнюю и верхнюю грани, а также наименьший и наибольший элементы (в слу- чае их существования), если
a) A = x |
|
Z |
|
| |
3x − 1 |
≥ − |
1; x < 0 ; |
|
|
|
|
|
||||||||||||
|
{ |
|
|
|
|
x + 1 |
|
|
|
|
} |
n2 − 1 |
|
|
|
|
||||||||
á) A = |
|
x |
|
|
Q |
|
x |
|
0; |
x |
|
1 |
|
|
< x |
|
; â) A = |
|
n |
|
N : |
|||
|
{ |
|
|
|
|
| |
|
|
≥ |
| |
|
− |
|
| |
|
} |
{ |
|
| |
|
|
} |
||
|
|
|
|
|
|
|
|
|
n |
|
||||||||||||||
8

Вариант •6
1. Найдите все элементы числовых множеств A; B; A B; A ∩B;
A \ B; B \ A; A∆B; åñëè |
1 |
|
{ |
15 |
|
} |
|||
24 |
|
|
|
||||||
à) A = {x [− ; ] | cos 2x < |
2 |
} ; B = |
|
x R | 3x2 − 7x + 2 < 0 |
; |
||||
á) A = {x N | |
|
N} ; B = {x N | x > |
|
} : |
|
||||
x |
x + 2 |
|
|||||||
2*. Докажите равенство (A ∩ B) A = A.
3*. Докажите, что если (A) = (B), ãäå (A) - булеан, или совокупность всех подмножеств, множества A, (B)- булеан мно-
жества B, òî A = B. |
|
|
|
|
|
|
|
|
4. Докажите иррациональность числа log |
2 |
7: |
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
r − ; |
ãäå |
I; |
à |
r Q: |
||||
5. Докажите иррациональность числа |
|
|
||||||
6*. Докажите, что |a| < c; ãäå c > 0, тогда и только тогда, когда
−c < a < c .
7. Решите уравнение | − x2 + 2x − 3| = 1:
√
8. Решите неравенство (x + 1)2 ≤ −x − 1:
9*. Докажите методом математической индукции справедливое для всех натуральных чисел равенство
1 |
|
1 |
1 |
|
n |
|
|
|
+ |
|
+ : : : + |
|
= |
|
: |
1 · 2 |
2 · 3 |
n · (n + 1) |
n + 1 |
||||
10. Выясните, является ли множество A ограниченым снизу, огра-
ниченным сверху, ограниченным, и найдите его нижнюю и верхнюю грани, а также наименьший и наибольший элементы (в слу- чае их существования), если
a) A = x |
|
Q |
|
7x − 10x2 − 1 > 0 ; |
|
|
|
|
|
|
||||||
{ |
|
|
| |
|
|
|
|
|
} |
|
n2 + 1 |
|
|
|
||
|
|
x |
− |
2 |
|
|
|
|
||||||||
á) A = x |
|
R |
|
|
|
|
|
1 , â) A = |
|
|
|
n |
|
N : |
||
|
| √x + 4 |
≥ |
{ 3n2 | |
|
||||||||||||
{ |
|
} |
|
} |
||||||||||||
Вариант •7
1. Найдите все элементы числовых множеств A; B; A B; A ∩B; A \ B; B \ A; A∆B; åñëè
9

{ |
| x |
|
} |
{x { |
| |
|
|
|
2− x |
} |
} |
|||||
à) A = {x |
|
[0; 2 ] |
| sin 3x ≥ 0} ; B = |
x |
R | −x2 |
− 5x + 6 ≥ |
0 ; |
|||||||||
á) A = x Z |
25 |
|
Z ; B = |
Z |
x 10 |
> 1 : |
|
|||||||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
||
2*. Докажите равенство A \ (A \ B) = A ∩ B. |
|
|
||||||||||||||
3*. Докажите, что множество |
A ∩ B есть элемент множества |
|||||||||||||||
(A B), ãäå (A B) - булеан, или совокупность всех подмно- |
||||||||||||||||
жеств, множества A B. |
|
√ |
|
|
|
: |
|
|
|
|
||||||
4. Докажите иррациональность числа |
12 |
|
|
|
||||||||||||
5. Докажите иррациональность числа |
√ |
|
; ãäå |
I; à |
|
|||||||||||
r · |
|
|||||||||||||||
r Q \ {0}:
6*. Докажите, что |a| > c; ãäå c > 0, тогда и только тогда, когда a < −c èëè a > c.
7.Решите уравнение |(x2+3x+8)+(2x−1)| = |x2+3x+8|+|2x−1|:
8.Решите неравенство |2x − 1| < |x − 1|:
9*. Докажите методом математической индукции справедливое для всех натуральных чисел равенство
1 |
+ |
1 |
+ : : : + |
1 |
|
= |
n |
: |
1 · 5 |
5 · 9 |
(4n − 3) · (4n + 1) |
4n + 1 |
|||||
10. Выясните, является ли множество A ограниченым снизу, огра-
ниченным сверху, ограниченным, и найдите его нижнюю и верхнюю грани, а также наименьший и наибольший элементы (в слу- чае их существования), если
a) A = {x I | log3(2x − 1) < 0} ; |
|
|
|
|
|
||||||||
{ |
|
|
| |
√ |
|
|
≥ |
} |
{2n | |
|
|
} |
|
|
x + 4 |
|
|||||||||||
á) A = x |
|
R |
|
|
x − 2 |
|
1 ; â) A = |
1 |
|
n |
|
N : |
|
|
|
|
|
|
|
|
|||||||
Вариант •8
1. Найдите все элементы числовых множеств A; B; A B; A ∩B;
A \ B; B \ A; A∆B; åñëè
à) A = x R | x3 − 5x2 − 6x < 0 ; B = x R | x3 − 4x < 0 ;
|
|
|
|
|
20 |
|
|
|
|
|
|
x2 |
|
2x |
|
1 |
|
|
|
á) A = |
{ x |
|
N |
| |
|
N ; B = x} |
|
N |
| |
{ |
− |
|
− |
|
< 1 : |
} |
|||
x |
|
|
x + 1 |
|
|||||||||||||||
|
{ |
|
} |
{ |
|
|
} |
|
|||||||||||
2*. Докажите равенство A ∩ (B \ C) = (A \ C) ∩ (B \ C).
10

3*. Докажите равенство (A ∩ B) = (A) ∩ (B).
4. Докажите иррациональность числа |
log5 3: |
||
|
√ |
|
; ãäå I; à |
5. Докажите иррациональность числа |
r= |
||
r Q \ {0}:
6*. Докажите, что для всех чисел a è b справедливо неравенство
|a − b| ≥ |a| − |b|:
7. Решите уравнение |x2 + 4x + 2| = 5x + 16 :
3
8. Решите неравенство ||x + 1| − |x − 1|| < 1:
9*. Докажите методом математической индукции справедливое для всех натуральных чисел равенство
1 |
+ |
1 |
+ : : : + |
1 |
= |
n |
: |
|
|
|
|
||||
1 · 3 |
3 · 5 |
(2n − 1) · (2n + 1) |
2n + 1 |
10. Выясните, является ли множество A ограниченым снизу, огра-
ниченным сверху, ограниченным, и найдите его нижнюю и верхнюю грани, а также наименьший и наибольший элементы (в слу- чае их существования), если
a) A = x R | log3 |
(x2 + 1) − log3 (2x + 3) ≤ 0 ; |
} |
|||||||||||
{ |
|
|
| |
|
|
|
≥ |
} |
{ |
n |
| |
|
|
á) A = {x |
|
Q |
|
21 |
|
2x |
|
4 ; â) A = |
|
n + 1 |
|
n} |
N : |
|
|
|
|
|
|
|
|
||||||
Вариант •9
1. Найдите все элементы числовых множеств A; B; A B; A ∩B;
A \ B; B \ A; A∆B; åñëè |
|
|
|
|
|
|
|
|
|
(3 − x) · (x + 1) > 0 ; |
||||||||||||
à) A = x |
|
R |
x2 > 5x |
− |
6 ; B = x |
|
R x2 |
|||||||||||||||
á) |
|
{ |
|
| |
5 |
|
} |
{ |
x2 |
+| 9x· |
+ 20 |
|
|
} |
||||||||
|
A = |
{x Z | |
|
Z} |
; B = {x Z | |
|
|
|
|
|
|
|
> 0} : |
|||||||||
|
x |
|
|
|
x + 4 |
|
||||||||||||||||
2*. Докажите включение A ∩ B ∩ C A \ (A \ (B C)). |
|
|||||||||||||||||||||
3*. Докажите, что A = B, тогда и только тогда, когда |
|
|
||||||||||||||||||||
(A \ B) (B \ A) = . |
|
|
|
√ |
|
: |
|
|
|
|
|
|
|
|
||||||||
4. Докажите иррациональность числа |
6 |
√ |
|
|
|
|
|
|
|
|||||||||||||
5. Докажите иррациональность числа |
|
r · |
|
|
ãäå |
|
|
à |
||||||||||||||
|
; |
I; |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
r Q \ {0}:
6*. Докажите, что равенство |a − b| = |a| − |b| справедливо тогда
11

и только тогда, когда ab ≥ 0 è |a| ≥ |b|.
7. |
Решите уравнение | cos x| − cos x − 3 = 0: |
||
8. |
Решите неравенство x2 + 2√ |
(x + 3)2 |
− 10 ≤ 0: |
9*. Докажите методом математической индукции справедливое для всех натуральных чисел равенство
1 |
+ |
1 |
+ : : : + |
1 |
|
= |
n |
: |
|
|
|
|
|
||||
1 · 4 |
4 · 7 |
(3n − 2) · (3n + 1) |
3n + 1 |
|||||
10. Выясните, является ли множество A ограниченым снизу, огра-
ниченным сверху, ограниченным, и найдите его нижнюю и верхнюю грани, а также наименьший и наибольший элементы (в слу- чае их существования), если
a) A = {x R | log3(x + 1) − log3 (2x − 3) ≥ 0} ; |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
á) A = {x I | x2 |
− x − 3 ≤ 0} ; â) A = { |
|
|
|
+ 1 |
|
| n N} : |
|
|
||||||||||||||
3n |
|
|
|
||||||||||||||||||||
|
|
n |
|
|
|||||||||||||||||||
|
|
|
|
|
Вариант •10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. Найдите все элементы числовых множеств A; B; A B; A ∩B; |
|||||||||||||||||||||||
A \ B; B \ A; A∆B; åñëè |
|
|
|
|
|
|
|
|
|
|
|
2 |
x |
|
|
2 |
|
||||||
|
|
|
|
sin 2x > 0} ; B = {x R | |
x |
|
|
|
0} ; |
||||||||||||||
à) A = {x [0; 2 ] |
| |
|
− |
|
− |
|
≥ |
||||||||||||||||
|
|
|
|
|
|||||||||||||||||||
|
|
|
x |
|
|
|
|||||||||||||||||
2*. |
{ |
x |
|
} |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
á) A = x N | |
5 |
|
N; x < 15 ; B = {x N | |
|
|
x − 1 |
|
|
< 4} : |
|
|||||||||||||
|
Докажите равенство |
(A ∩ B) \ C = (A \ C) ∩ (B \ C) |
. |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
3*. Докажите, что если A ∩ B = , òî (A) ∩ (B) = { }. |
|
|
|||||||||||||||||||||
4. Докажите иррациональность числа log6 8: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
5. Докажите иррациональность числа |
|
√ |
|
|
ãäå |
I; |
à |
|
|
|
|||||||||||||
r= |
; |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
r Q \ {0}:
6*. Докажите, что для всех чисел a è b справедливо неравенство
||a| − |b|| ≤ |a − b|.
7.Решите уравнение | tg x| + tg x − 2 = 0:
8.Решите неравенство ||3 − x| − 2| ≤ |x − 1|:
9*. Докажите методом математической индукции справедливое для всех натуральных чисел равенство
(1 − |
1 |
) · |
(1 − |
1 |
) : : : |
(1 − |
1 |
) = |
n + 2 |
: |
|
|
|
|
|||||||
4 |
9 |
(n + 1)2 |
2n + 2 |
12

10. Выясните, является ли множество A ограниченым снизу, огра-
ниченным сверху, ограниченным, и найдите его нижнюю и верхнюю грани, а также наименьший и наибольший элементы (в слу-
чае их существования), если |
|
{ |
} |
||||||
|
n + 2 |
|
− |
|
|
||||
a) A = {x R | |
log3 |
x + 1 |
≤ 0} ; á) A = |
x Q | |
x2 ≤ 2 ; |
||||
2x |
|
3 |
|||||||
â) A = { |
|
| n N} |
: |
|
|
|
|
||
n − 2 |
|
|
|
|
|||||
Вариант •11
1. Найдите все элементы числовых множеств A; B; A B; A ∩B;
A \ B; B \ A; A∆B; åñëè |
|
|
; B = |
{x R | x + 5 |
≥ 2} ; |
|
||||||||
à) A = |
x [0; ] | tg 2x < √3 |
|
||||||||||||
|
{ |
|
|
|
|
|
|
|
x + 6 |
x3 + 2x2 |
||||
2*. |
|
(A }B) C A (B C) |
|
|||||||||||
|
{ |
|
|
|
} |
|
4 |
|
||||||
á) A = x N | x2 − x − 2 > 0 ; B = {x N | |
x − |
3 |
|
30 |
< 0} : |
|||||||||
x2 |
x |
− |
||||||||||||
|
Докажите включение |
|
|
\ |
\ |
− |
|
|
|
|||||
|
|
. |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||||
3*. Докажите, что если A B, òî (A) (B): |
|||
4. Докажите иррациональность числа |
√ |
45 |
: |
5. Докажите иррациональность числа |
r + ; ãäå I; à r Q: |
||
6*. Докажите, что равенство |a−b| = ||a|−|b|| справедливо тогда и только тогда, когда a · b ≥ 0.
7.Решите уравнение |x + 3| + |2x − 1| = 7:
8.Решите неравенство |x2 − 2x| > x2 − |2x|:
9*. Докажите методом математической индукции справедливое для всех натуральных чисел равенство
1 |
+ |
2 |
+ |
3 |
+ : : : + |
n |
= 2 − |
n + 2 |
: |
2 |
22 |
23 |
2n |
2n |
10. Выясните, является ли множество A ограниченым снизу, огра-
ниченным сверху, ограниченным, и найдите его нижнюю и верхнюю грани, а также наименьший и наибольший элементы (в слу- чае их существования), если
a) A = {x R | log3 (x + 1) + log3 (2x − 3) < 1} ; |
|
|||||
|
|
|
|
5n + 2 |
|
|
á) A = {x Z | |
√2x2 − 4x + 9 > 1} ; â) A = { |
| n N} : |
||||
3n |
||||||
13

Вариант •12
1. Найдите все элементы числовых множеств A; B; A B; A ∩B;
A \ B; B \ A; A∆B; åñëè |
|
1 |
|
|
{ |
|
|
|
|
1 |
|
|
|
1 |
|
} |
||||
à) A = {x [− ; ] | cos 3x < |
} ; B = |
x R | x2 + 5x + 6 < 0 |
; |
|||||||||||||||||
|
|
|||||||||||||||||||
|
2 |
|||||||||||||||||||
á) A = x Z | x2 + 5x ≥ 0 ; B = {x Z | |
|
≤ − |
|
} : |
|
|||||||||||||||
x − 3 |
10 |
|
||||||||||||||||||
2*. |
Докажите равенство |
(A} |
B) |
|
C = (A |
|
C) |
|
(B |
|
C). |
|
||||||||
{ |
\ |
\ |
\ |
\ |
|
|||||||||||||||
|
|
\ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3*. Докажите, что если A B, òî B A:
4.Докажите иррациональность числа lg 2:
5.Докажите иррациональность числа =r; ãäå I; à r Q\{0}: 6*. Докажите, что равенство |a − b| = |a| + |b| справедливо тогда и только тогда, когда a · b ≤ 0.
7. Решите уравнение |5 − 2x| + |x + 3| = 2 − 3x:
1
8. Решите неравенство |x − 1| < 4 − x:
9*. Докажите методом математической индукции справедливое для всех натуральных чисел равенство
1 |
+ |
2 |
+ |
3 |
+ : : : + |
n |
= |
3 |
· (1 − |
2n + 3 |
) : |
|
|
|
|
|
|
||||||
3 |
32 |
33 |
3n |
4 |
3n+1 |
10. Выясните, является ли множество A ограниченым снизу, огра-
ниченным сверху, ограниченным, и найдите его нижнюю и верхнюю грани, а также наименьший и наибольший элементы (в слу- чае их существования), если
a) A = {x R | log (x + 1) + log (2x − 3) > 1} ;
{ √3 3 }
á) A = x Q | 2x2 − 4x + 9 > 1 ;
{ }
1
â) A = n − 10 | n N; n ≠ 10 :
Вариант •13
1. Найдите все элементы числовых множеств A; B; A B; A ∩B; A \ B; B \ A; A∆B; åñëè
14

|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x + 5 |
|||
à) A = {x [− ; ] | sin 2x > |
|
|
} ; B = {x |
R |
| |
|
> 3} ; |
|||||||||||||||||||||
2 |
x + 3 |
|||||||||||||||||||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
2x |
|
|
|
|
||||
á) A = {x Z | |
|
Z} ; B = {x Z |
| |
|
|
− |
≥ 1} : |
|||||||||||||||||||||
x |
x2 + 3 |
|||||||||||||||||||||||||||
2*. Докажите равенство (A ∩ B) \ C = (A \ C) ∩ (B \ C). |
||||||||||||||||||||||||||||
3*. Докажите, что если A |
|
|
B |
|
|
|
|
C, òî A |
B |
|
C: |
|||||||||||||||||
|
|
иррациональность числа |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
4. |
Докажите |
|
|
|
|
|
\ |
|
|
|
|
|
|
3 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√3: |
|
|
|
|
|
|||||
5. |
Докажите иррациональность числа √ |
|
=r; |
ãäå I; à |
||||||||||||||||||||||||
|
||||||||||||||||||||||||||||
r Q \ {0}: |
|
равенство |
a |
|
|
|
= |
|a| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
6*è. Докажите. |
|
|
, справедливое для всех чисел |
|||||||||||||||||||||||||
b |
|b| |
|||||||||||||||||||||||||||
a |
b |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
7. |
Решите уравнение |x + 2| = |
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
||||||||||||
3 |
− |
x |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
8. |
Решите неравенство |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|x + 2| − |x| > 1: |
|
|
|
|
|
|||||||||||||||||
9*. Докажите методом математической индукции справедливое для всех натуральных чисел равенство
|
7 |
|
+ |
|
7 |
+ : : : + |
|
|
|
7 |
|
= 1 − |
1 |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
· |
8 |
8 |
· |
15 |
(7n |
− |
6) |
· |
(7n + 1) |
7n + 1 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
10. Выясните, является ли множество A ограниченым снизу, огра-
ниченным сверху, ограниченным, и найдите его нижнюю и верхнюю грани, а также наименьший и наибольший элементы (в слу-
чае их существования), если |
|
â) |
|
|
}n2 + 2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
á) |
|
{ |
|
5x 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
√ |
|
|
|
√ |
6 − 5x ≥ 0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
a) A = x R | 5x − 6 + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
A = |
{x I | |
8 |
− |
≤ 0} |
|
; A = { |
|
|
|
|
|
| n N} : |
|
|
|
|
||||||||||||
|
4x |
|
|
|
n |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Вариант •14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1. Найдите все элементы числовых множеств A; B; A B; A ∩B; |
|||||||||||||||||||||||||||||
A \ B; B \ A; A∆B; åñëè |
|
|
|
|
|
|
|
|
|
|
|
(x |
2) |
2 |
|
|
25 |
; |
|
||||||||||
à) |
A = {x [0; 2 ] | sin 2x < 0} ; B = |
x R |
| |
|
|
≤ |
|
||||||||||||||||||||||
á) |
|
6 |
|
− |
3 |
|
|
≤} |
0 : |
||||||||||||||||||||
A = {x Z | |x − 3| ≤ 7} |
; B = |
x |
|
Z |
| |
x |
|
+ 9x |
− |
18 |
|||||||||||||||||||
|
{ |
|
C) |
|
(B |
|
|
|
|
} |
|||||||||||||||||||
2*. Докажите равенство |
|
(A \ B) |
C = (A |
∩ |
\ |
\ |
C). |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
∩ |
{ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
3*. Докажите, что если A B C, òî A \ B C: 4. Докажите иррациональность числа lg 5:
15

5. Докажите иррациональность числа √r · √ ; ãäå I; à
r Q \ {0}: √
6*. Докажите неравенство a2 + b2 ≤ |a| + |b|, справедливое для всех чисел a è b.
7.Решите уравнение x2 + |x − 2| − 10 = 0:
8.Решите неравенство |x2 − 2x − 3| > x2 − 2x − 3:
9*. Докажите методом математической индукции справедливое для всех натуральных чисел равенство
1 |
|
+ |
|
|
1 |
+ : : : + |
|
|
|
|
|
1 |
|
|
|
|
|
|
= |
1 |
(1 |
− |
|
1 |
|
) : |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
1 · 3 |
3 · 5 |
(2n − 1) · (2n + 1) |
2 |
2n + 1 |
|
|
|
||||||||||||||||||||||||||||||||||
10. Выясните, является ли множество A ограниченым снизу, огра- |
|
||||||||||||||||||||||||||||||||||||||||
ниченным сверху, ограниченным, и найдите его нижнюю и верх- |
|
||||||||||||||||||||||||||||||||||||||||
нюю грани, а также наименьший и наибольший элементы (в слу- |
|
||||||||||||||||||||||||||||||||||||||||
чае их существования), если2 |
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
a) A = x R | −(x − 1) + 6x − 12 ≥ 0 ; |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
{ |
|
|
|
|
|
|
2x + 5 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
} |
|
|
|
|
|
|
|
|
|
|||||||||
á) A = {x Q |
| |
|
|
|
|
|
> 1} ; â) A = { |
|
|
|
| n N} : |
|
|
|
|
||||||||||||||||||||||||||
|
2 + 5x |
|
n + 2 |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант •15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1. Найдите все элементы числовых множеств A; B; A B; A ∩B; |
|
||||||||||||||||||||||||||||||||||||||||
A \ B; B \ A; A∆B; åñëè |
|
|
|
|
|
x R | |x| + 1 ≥ (x + 1) |
2 |
} |
; |
||||||||||||||||||||||||||||||||
à) A = |
|
x |
|
|
[− ; ] | ctg 2x < 1} ; B = |
|
|
||||||||||||||||||||||||||||||||||
á) A = |
{ x |
|
N |
|
16 |
|
|
N ; B = x |
{N |
|
|
x2 |
|
7x + 1 |
|
0 : |
|
|
|||||||||||||||||||||||
|
|
{ |
|
|
| |
|
|
|
|
|
|
} |
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
− |
|
|
|
≤ |
} |
|
|
|
|||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
B) |
C. |
|
|
|
|
||||||||||||||||||||
2*. Докажите равенство |
A \ |
|
C) = (A |
\ |
\ |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(B { |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
3*. Докажите, что если A |
|
B = B, òî A |
|
B: |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
4. Докажите |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
иррациональность числа |
√2: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
r Q \ {0}: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
r=√ |
|
|
|
|
|
|
|
|
, ñïðà- |
|
|||||||||||||
5. Докажите иррациональность числа |
|
|
|
|
|
; ãäå |
|
I; à |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
√ √
6*. Докажите неравенства |a| ≤ a2 + b2 è |b| ≤ a2 + b2 ведливые для всех чисел a è b.
7.Решите уравнение |x + 6| = |x2 − 5x + 9|:
8.Решите неравенство 3x2 − |x − 3| > 9x − 2:
16

9*. Докажите методом математической индукции справедливое для всех натуральных чисел равенство
1 |
+ |
1 |
+ : : : + |
1 |
= |
1 |
· ( |
1 |
− |
1 |
) : |
|
|
|
|
|
|
||||||
3 · 7 |
7 · 11 |
(4n − 1) · (4n + 3) |
4 |
3 |
4n + 3 |
10. Выясните, является ли множество A ограниченым снизу, огра-
ниченным сверху, ограниченным, и найдите его нижнюю и верхнюю грани, а также наименьший и наибольший элементы (в слу- чае их существования), если
a) A = x |
|
R |
| |
√ |
2 − x |
≥ |
2 ; á) A = x |
|
I |
| |
32 |
|
x2 |
≤ |
1 |
; |
|||
3 + x |
|
81 |
|||||||||||||||||
{ |
|
} |
{ |
|
|
|
} |
||||||||||||
â) A = { |
|
2 + 3 |
|
| n N} : |
|
|
|
|
|
|
|
|
|
|
|||||
2n |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
3n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Указания к решению задач индивидуального задания по теме "Множества"
Решение задач нулевого варианта
Задача 1
Найдите все элементы числовых множеств A; B; A B; A∩B;
A \ B; B \ A; A∆B; åñëè |
|
|
|
|
|
|
|
2 |
|
||||||
à) A = x |
[− =2; =2] | tg 3x > 1} ; B = x R |
| |x| < (x + 1) ; |
|||||||||||||
á) A = { x |
|
N |
|
20 |
|
N ; B = x |
|
N{ |
x2 |
|
14x + 33 |
|
0 : |
} |
|
|
| x |
|
− |
≤ |
|||||||||||
{ |
|
} |
{ |
|
| |
|
} |
|
|||||||
Решение.
Для того, чтобы найти элементы указанных множеств, необходимо воспользоваться определениями объединения, пересече- ния и разности двух множеств. Но прежде необходимо понять, из каких элементов состоят данные множества. Для этого вам потребуется решить либо квадратное, либо дробно-рациональное, либо тригонометрическое неравенства.
17
Как решить квадратное неравенство?
1.Найти корни квадратного трехчлена (например, через дискриминант).
2.Изобразить корни квадратного трехчлена на числовой прямой, эти корни (если их два различных) разбивают числовую прямую на три промежутка.
3.Определить знак квадратного трехчлена на каждом промежутке.
Как решить дробно-рациональное неравенство?
1.Разложить на множители числитель и знаменатель дроби.
2.Применить метод интервалов: найти корни сомножителей числителя и знаменателя; изобразить их в порядке возрастания на числовой прямой; определить знак дробно-рационального выражения на каждом промежутке.
Как решить тригонометрическое неравенство? Воспользоваться графиком соответствующей тригонометрической функции или тригонометрическим кругом.
Пусть a (−1; 1), ò.å. |a| < 1.
Тогда решением неравенства cos x ≥ a будет совокупность промежутков вида [− arccos a + 2 n; arccos a + 2 n]; n Z
(ðèñ. 1).
arccos a+2πn |
arccos a+2πn |
|
a |
a |
-arccos a+2πn |
2π-arccos a+2πn |
! и #. 1 |
! и #. 2 |
Напомним, что арккосинусом числа a, |a| ≤ 1, называется такое число b из промежутка [0; ], что cos b = a.
Решением неравенства cos x ≤ a будет совокупность промежутков вида [arccos a + 2 n; 2 − arccos a + 2 n]; n Z
18
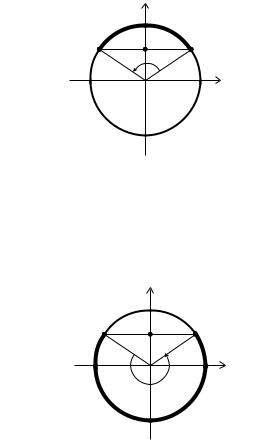
(ðèñ. 2).
Решением неравенства sin x ≥ a будет совокупность промежутков вида [arcsin a + 2 n; − arcsin a + 2 n]; n Z (ðèñ. 3).
π-arcsin a+2πn |
a |
arcsin a+2πn |
! и #. 3
Напомним, что арксинусом числа a, |a| ≤ 1, называется такое число b из промежутка [− =2; =2], ÷òî sin b = a.
Решением неравенства sin x ≤ a будет совокупность промежутков вида [− − arcsin a + 2 n; arcsin a + 2 n]; n Z (ðèñ.4).
−π-arcsin a+2πn |
a |
arcsin a+2πn |
! и #. 4
Пусть теперь a - произвольное число.
Решением неравенства tg x ≥ a будет совокупность промежутков вида [arctg a + n; =2 + n); n Z.
Напомним, что арктангенсом числа a называется такое число b из промежутка (− =2; =2), ÷òî tg b = a.
19
Решением неравенства tg x ≤ a будет совокупность промежутков вида (− =2 + n; arctg a + n]; n Z.
Решением неравенства ctg x ≥ a будет совокупность промежутков вида ( n; arcctg a + n]; n Z.
Напомним, что арккотангенсом числа a называется такое число b из промежутка (0; ), что ctg b = a.
Решением неравенства ctg x ≤ a будет совокупность промежутков вида [arcctg a + n; + n); n Z.
Неравенства вида cos kx ≥ a (соответственно, sin kx ≥ a, tg kx ≥ a, ctg kx ≥ a) решают с помощью замены kx = t, при этом получают неравенство вида cos t ≥ a ( соответственно, sin t ≥ a, tg t ≥ a, ctg t ≥ a), и, следовательно, промежутки для t, затем находят x = t=k:
а) Пусть даны множества A = {x [− =2; =2] | tg 3x > 1} ; B = {x R | |x| < (x + 1)2} :
Найдем элементы множества A. Это множество состоит из чисел x отрезка [− =2; =2], для которых выполняется неравенство tg 3x > 1. Найдем все такие числа, т.е. решим неравенство tg 3x > 1 и из всех его решений выберем только те, которые принадлежат отрезку [− =2; =2].
Пусть 3x = t, тогда tg t > 1 и, следовательно,
t (arctg 1 + n; =2 + n) =4 + n < t < =2 + n
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
n |
|||||||||
=4+ n < 3x < =2+ n |
|
|
|
+ |
|
|
|
|
< x < |
|
|
+ |
|
; n Z : |
|||||||||||||||||||||||||||||
12 |
3 |
6 |
3 |
||||||||||||||||||||||||||||||||||||||||
По условию x [− =2; =2], тогда найдем такие n Z, äëÿ |
|||||||||||||||||||||||||||||||||||||||||||
которых одновремено справедливы неравенства |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
≥ − |
|
|
|
|
|
|
n |
|
≤ |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
è |
|
|
|
+ |
|
|
|
|
|
|
|
|
: |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
12 |
|
3 |
2 |
6 |
|
|
|
3 |
|
2 |
|
|
|
|
|
|
|
||||||||||||||||||||
Такими значениями для n будут −1; |
0; |
1 (проверьте!). |
|||||||||||||||||||||||||||||||||||||||||
|
Итак, решениями неравенства tg 3x > 1 в промежутке [− =2; =2] |
||||||||||||||||||||||||||||||||||||||||||
будут все значения x, принадлежащие объединению промежут- |
|||||||||||||||||||||||||||||||||||||||||||
êîâ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
( |
|
− |
|
; |
|
− |
|
|
) |
( |
|
; |
|
|
) ( |
|
+ |
|
|
; |
|
+ |
|
|
) ; ò.å. |
|||||||||||||||||
|
12 |
3 |
6 |
3 |
12 |
6 |
12 |
3 |
6 |
3 |
|||||||||||||||||||||||||||||||||
20
A = (− 4 ; − 6 ) (12 ; 6 ) (512 ; 2 ) :
Найдем элементы множества B. Это множество состоит из всех чисел x, удовлетворяющих неравенству |x| < (x + 1)2. Ðå- шим это неравенство. Так как (x + 1)2 ≥ 0 ïðè âñåõ x, то, применяя свойство модуля |x| < c −c < x < c, имеем:
|x| < (x + 1)2 −(x + 1)2 < x < (x + 1)2x > −(x + 1)2 è x < (x + 1)2
x > −x2 − 2x − 1 è x < x2 + 2x + 1x2 + 3x + 1 > 0 è x2 + x + 1 > 0
√√
|
|
|
|
|
|
x < |
|
−3 − |
5 |
|
èëè x > |
−3 + |
5 |
: |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||
Èòàê, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
− |
3 − |
√ |
|
|
) |
( |
−3 + |
√ |
|
; + |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
B = |
|
|
; |
5 |
5 |
: |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
(−∞ |
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
∞) |
|
|
|
|||||||||||||||||||||||||
Изобразим множества A è B на числовой прямой (рис. 5). |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
π |
|
|
|
|
π |
|
|
|
π |
|
|
5π |
π |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
6 |
|
|
|
12 |
6 |
|
12 |
2 |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
3−?5 |
|
|
|
|
|
|
|
|
|
−3+?5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
! и #. 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Теперь несложно найти A B; A ∩ B; A \ B; B \ A; A∆B: |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
A |
|
B = |
; |
|
|
3 − 5 |
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
−3 + 5 |
; + |
; |
|||||||||||||||||
|
− |
|
) (− 4 |
− |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
(−∞ |
2 |
|
|
|
|
6 ) ( |
2 |
|
|
∞) |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
A ∩ B = ( |
|
; |
|
) ( |
|
|
; |
|
|
) ; |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
12 |
6 |
12 |
|
2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
21

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
A |
\ B = (− |
|
; − |
|
|
) ; |
|
|
|
|
|
|
|||||||
|
|
|
4 |
6 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
3 − |
√ |
|
|
|
|
|
|
−3 + √ |
|
|
|
|
|||||
B |
|
A = |
; |
|
5 |
|
|
|
5 |
; |
|
|
||||||||||
\ |
|
|
|
|
|
|
|
|
|
|
|
|
12 ) |
|||||||||
|
|
(−∞ |
− |
2 |
|
|
) ( |
2 |
|
|
|
|||||||||||
|
|
|
( |
|
5 |
) ( |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
; |
|
|
|
; +∞) ; |
|
|
|
|||||||||||
|
|
|
6 |
12 |
|
2 |
|
|
|
|||||||||||||
|
|
|
A∆B = (A \ B) (B \ A): |
N} ; |
||||||||||||||||||
б)Пусть даны множества A = {x N | x |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
||
{ |
|
|
|
|
|
|
|
} A |
|
|
|
|
|
|
|
|
|
|
|
|||
B = x N | x2 − 14x + 33 ≤ 0 : |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Найдем элементы множества |
|
: это все натуральные числа |
||||||||||||||||||||
x, которые являются делителями числа 20 (т.е. делят число 20 нацело). Перечислим их: 1, 2, 4, 5, 10, 20. Следовательно,
A = {1; 2; 4; 5; 10; 20}:
Найдем элементы множества B: это все натуральные числа x, которые удовлетворяют неравенству x2 − 14x + 33 ≤ 0. Числа 3 и 11 являются корнями квадратного трехчлена x2 − 14x + 33, следовательно, все числа принадлежащие отрезку [3; 11] являются решениями неравенства x2 − 14x + 33 ≤ 0, но нас интересуют только натуральные числа этого отрезка, поэтому
B = {3; 4; 5; 6; 7; 8; 9; 10; 11}:
Тогда A B = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 20};
A∩ B = {4; 5; 10};
A\ B = {1; 2; 20};
B \ A = {3; 6; 7; 8; 9; 11};
A∆B = (A \ B) (B \ A) = {1; 2; 3; 6; 7; 8; 9; 11; 20}:
22
Задача 2
∩
Докажите равенство A \ (B C) = (A \ B) (A \ C).
Решение.
Сначала можно убедиться в истинности равенства с помощью рисунка, изобразив множества A; B è C в виде пересекающих-
ся кругов.
Доказать равенство двух множеств A è B, значит доказать два включения: A B è B A. Сначала показывают, что все элементы множества A содержатся во множестве B, а затем, что все элементы множества B содержатся во множестве A. Например, чтобы доказать включение A B, фиксируют какой-либо элемент x â A и путем логических рассуждений, основанных на
определениях и свойствах, устанавливают, что этот элемент принадлежит и B. В силу того, что элемент в A выбран произволь-
ным образом, доказанное распространяют на все элементы множества A.
Вернемся к нашему примеру. Докажем сначала включение
∩
A \ (B C) (A \ B) (A \ C). Пусть x A \ (B C), x - произ-
вольно выбран в этом множестве, тогда по определению разности множеств получим: x A è x = B C, далее, используя опреде-
ление объединения множеств , имеем: x A è (x = B è x = C). Применяя к последнему высказыванию об элементе x соответ-
ствующие свойства алгебры высказываний, получим конъюнкцию двух высказываний: (x A è x = B) è (x A è x = C).
Теперь, применяя к полученным высказваниям определения разности и пересечения множеств, получим, что x A \ B è
x A \ C, ò.å. x (A \ B) ∩ (A \ C). В силу произвольности x |
||
Справедливость |
∩ |
A \ (B C) (A \ B) ∩ (A \ C) |
имеем: A \ (B C) (A \ B) |
|
(A \ C). |
включения доказывается аналогично (для этого необходимо провести обрат-
ные рассуждения - "снизу вверх"). Поскольку
∩
A \ (B C) (A \ B) (A \ C) è (A \ B) ∩ (A \ C) A \ (B C),
∩
òî A \ (B C) = (A \ B) (A \ C), что и требовалось доказать.
23

Задача 3
Докажите, что если A B = A, òî B A:
Решение.
Äàíî: A B = A
Доказать: B A.
Доказательство: Требуется доказать, что при заданном условии множество B является частью множества A, ò.å. ÷òî âñå ýëå-
менты множества B принадлежат и множеству A.
Пусть x - произвольный элемент множества B, тогда (в силу
определения объединения множеств ) x также элемент объединения множества B ñ каким-либо другим множеством, например с множеством A, ò.å. x - элемент множества B A, íî B A = A B (по свойсту объединения двух множеств), а A B = A по условию, тогда x - элемент множества A. В силу произвольности x, имеем, что любой элемент множества B принадлежит множеству A, ò.å. B A.
|
|
|
|
|
|
Задача 4 |
|
|
|
|
|
|
|
|
||
|
Докажите иррациональность числа √ |
|
: |
|
|
|
|
|||||||||
|
2 |
|
|
|
|
|||||||||||
|
Решение. |
|
|
|
|
|
√ |
|
|
|||||||
|
Докажем от противного. Пусть |
2 |
рациональное число. То- |
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||||
гда оно представимо в виде несократимой дроби |
p=q |
, ãäå p Z, |
||||||||||||||
|
|
, ò.å. √ |
|
|
|
|
|
|
|
|
|
|
|
. Èç ïî- |
||
|
N |
|
|
èëè |
2 |
|
2. Отсюда 2q2 |
= p2 |
||||||||
q |
|
2 = p=q |
|
2 = p |
=qделится на 2, но тогда само |
|||||||||||
следнего равенства следует, что p2 |
|
|
|
|
|
|
|
|
|
|||||||
число p делится на 2, и, следовательно, p2 делится на 4, т.е. p2 = 4k; ãäå k N.
Èòàê, 2q2 = 4k; èëè q2 = 2k. Отсюда получаем, что q2 äå- лится на 2, а значит, и q делится на 2. Таким образом, получили, что и p, è q делятся на одно и то же число 2. Но мы предполагали, что дробь p=q несократима (т.е. числа p è q не имеют общих
делителей). Полученное противоречие приводит√ к выводу, что наше предположение√ о рациональности числа 2 неверно. Сле- довательно, число 2 - иррациональное.
24

Задача 5
√
Докажите иррациональность числа 3 r= ; ãäå I; à
r Q \ {0}:
Решение. |
√3 r= Q, ò.å. √3 r= = r1, |
Докажем от противного. Пусть |
тогда r= = r13, отсюда = r=r13. Получили, что - число
рациональное, но по условию оно ирра√öèîнальное. Полученное противоречие доказывает, что число 3 r= не может быть раци-
ональным, и, значит, оно иррациональное.
Задача 6
√
Докажите неравенство a2 + b2 ≤ |a| + |b|, справедливое для всех чисел a è b.
Решение.
Äàíî: a; b R
√
Доказать: a2 + b2 ≤ |a| + |b|
Доказательство: Так как обе части данного неравенства по-
ложительны для всех a; |
b R, имеем |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
2 |
2 |
|
2 |
2 |
|
+ b |
|
|
( |
2 |
2 |
|||
√a + b |
|
|
|2 |
a + b ) ≤ (2|a| + |b|) |
|||||||
|
≤ |a| |
2 | |
√2 |
||||||||
|
|
|
a + b |
≤ |a| + 2|a||b| + |b| |
|
||||||
a2 + b2 ≤ a2 + 2|a||b| + b2 0 ≤ 2|a||b| :
Таким образом, данное неравенство равносильно неравенству 2|a||b| ≥ 0, которое справедливо для всех чисел a è b.
Задача 7
Решите уравнение |x − 2| = |x2 − 5x + 6|:
Решение.
Для того, чтобы решить уравнение или неравенство, содержащие неизвестные под знаком модуля, необходимо раскрыть
25
знак модуля. Снять модуль с выражения A(x) мы можем в том
случае, если нам известно какой знак имеет это выражение при всех значениях входящей в него переменой: |A(x)| = A(x), åñëè
A(x) ≥ 0 è |A(x)| = −A(x), åñëè A(x) ≤ 0. Для определения
знака выражения под модулем достаточно найти нули (корни) этого выражения, т.е. те числа, в которых выражение принимает значение 0. В точках, находящихся слева или справа от этих корней, выражение под модулем сохраняет знак.
Вернемся к нашему уравнению. Выражение под модулем в левой части уравнения обращается в ноль при x = 2, а выраже-
ние под модулем в правой части уравнения обращеатся в ноль при x = 2 è x = 3. Имеем:
|x − 2| = |x2 − 5x + 6| |x − 2| = |(x − 2)(x − 3)|
|x − 2| = |x − 2||x − 3| :
Число x = 2 является решением данного уравнения. Найдем другие решения, отличные от 2. При x ≠ 2 имеем
|x − 2| = |x − 2||x − 3| |x − 3| = 1; x ≠ 2
x−3 = 1 èëè x−3 = −1; x ≠ 2 x = 4 èëè x = 2; x ≠ 2
x = 4 :
Ответ: x = 2 è x = 4.
Задача 8
Решите неравенство 4|x − 3| > |x2 + 2x − 3|:
Решение.
Сначала найдем значения переменной x, при которых выра-
жения под модулем левой и правой частей неравенства обращаются в ноль. Это числа 3, -3 и 1. Они разбивают всю числовую прямую на четыре промежутка: (−∞; −3]; (−3; 1]; (1; 3]; (3; +∞),
на каждом из которых все выражения под модулем сохраняют знак:
26

åñëè x (−∞; −3]; òî x2 + 2x − 3 ≥ 0; à x − 3 < 0; åñëè x (−3; 1]; òî x2 + 2x − 3 ≤ 0; à x − 3 < 0; åñëè x (1; 3]; òî x2 + 2x − 3 > 0; à x − 3 ≤ 0;
åñëè x (3; +∞); òî x2 + 2x − 3 > 0; è x − 3 > 0.
Раскрывая знак модуля на каждом из промежутков, получим совокупность четырех систем неравенств:
1) { |
x ≤ −3 |
|
|
|
|
|
−4(x − 3) > x2 + 2x − 3 |
|
|
|
|
|
|
2) |
−3 < x ≤ 1 |
|
|
|
|
|
{ |
−4(x − 3) > −x2 − 2x + 3 |
|
|
|
|
|
3) |
1 < x ≤ 3 |
|
|
|
|
|
{ |
−4(x − 3) > x2 + 2x − 3 |
|
|
|
|
|
4) { |
x > 3 |
|
|
|
|
|
4(x − 3) > x2 + 2x − 3 |
(−3 − |
√ |
|
|
|
|
Решением системы 1) является промежуток |
|
|
, |
|||
|
|
24; |
−3] |
|||
решением системы 2) является промежуток (−3; 1], решением си- |
||||||
стемы 3) является промежуток |
(1; −3+ |
√ |
|
|
, система 4) решений |
|
24) |
||||||
|
|
|
||||
не имеет. Совокупность решений всех четырех систем является решением заданного неравенства:
√ |
|
√ |
|
|
√ |
|
|
√ |
|
|
(−3− |
24; −3] (−3; 1] (1; −3+ 24) = (−3− |
|
24; −3+ |
24) : |
||||||
√√
Ответ: x (−3 − 24; −3 + 24).
Задача 9
Докажите методом математической индукции справедливое для всех натуральных чисел равенство
|
1 |
|
+ |
|
1 |
+ : : : + |
|
1 |
|
= |
1 |
· |
3n |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
5 |
· |
8 |
8 |
· |
11 |
(3n + 2) |
· |
(3n + 5) |
15 |
3n + 5 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
27

Решение.
Обозначим P (n) высказывание о переменной n N:
|
|
1 |
|
+ |
|
1 |
+ : : : + |
|
1 |
|
|
|
|
= |
|
1 |
· |
|
3n |
|
. |
|
|||
5 |
· |
8 |
8 |
· |
11 |
(3n + 2) |
· |
(3n + 5) |
15 |
|
3n + 5 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
· 3 |
3 · 1 |
|
|
|
|
||||||
1. Проверим истинность P (1): |
|
= |
|
- верно. |
|
||||||||||||||||||||
5 |
8 |
15 |
|
|
- èñ- |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + 5 |
|
|
|||||||||
2. Предположим теперь, что для· |
некоторого· |
n |
N P (n) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
тинно, и докажем, что это предположение влечет истинность
P (n + 1).
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||||||||
P (n + 1) : |
|
|
|
|
|
|
|
+ |
|
|
|
|
+ : : : + |
|
|
|
|
|
|
|
|
|
+ |
|||||||||||||||
|
|
|
5 · 8 |
|
8 · 11 |
(3n + 2) · (3n + 5) |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 3(n + 1) |
|
|||||||||
+ |
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
· |
|
|
|
|
|
: |
|||||||||||||||||
(3(n + 1) + 2) |
· |
(3(n + 1) + 5) |
15 |
3(n + 1) + 5 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как, согласно предположению, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
· |
3n |
|
|||||||||
|
|
|
|
+ |
|
|
|
|
|
+ : : : + |
|
|
|
|
|
= |
|
|
|
; |
||||||||||||||||||
5 |
· |
8 |
8 |
· |
11 |
|
(3n + 2) |
· |
(3n + 5) |
15 |
3n + 5 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
то левая часть равенства P (n + 1) примет вид |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
· |
|
3n |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
; |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
15 |
3n + 5 |
(3n + 5) |
· |
(3n + 8) |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
преобразуем получившееся выражение и покажем, что оно равно правой части равенства P (n + 1).
1 |
· |
3n |
+ |
|
|
1 |
|
|
|
|
|
|
|
|
= |
3n(3n + 8) + 15 |
= |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
15 |
3n + 5 |
(3n + 5) |
· |
(3n + 8) |
15(3n + 5)(3n + 8) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9n2 |
+ 24n + 15 |
|
|
|
|
|
(3n + 5)(3n + 3) |
|
||||||||||
|
|
= |
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
= |
|
||
|
|
15(3n + 5)(3n + 8) |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
15(3n + 5)(3n + 8) |
|
|||||||||||||||
|
|
|
|
|
|
(3n + 3) |
|
|
|
|
1 |
|
· |
|
3(n + 1) |
|
|||||
|
|
|
|
= |
|
|
|
= |
|
|
|
|
: |
|
|||||||
|
|
|
|
|
15(3n + 8) |
15 |
3(n + 1) + 5 |
|
|||||||||||||
Из 1 и 2, согласно принципу математической индукции, следует истинность P (n) ïðè âñåõ n N.
28

Задача 10
Выясните, является ли множество A ограниченым снизу, огра-
ниченным сверху, ограниченным, и найдите его нижнюю и верхнюю грани, а также наименьший и наибольший элементы (в слу- чае их существования), если
a) A = {x R | √ |
x |
|
|
2 |
|
|
|
|
|
|
|
|
2 |
1 |
|
|
|
− |
|
≥ 2} ; á) A = {x I | 24 x ≤ |
|
|
} ; |
||||||||||
3 |
|
x |
16 |
|||||||||||||
á') A = {x I | 24 x |
− |
|
|
1 |
|
} ; â) A = |
{ |
2 |
|
|
|
} : |
|
|||
2 |
≥ |
|
4n − |
3 |
| |
n N |
|
|||||||||
|
|
|
|
|||||||||||||
|
16 |
5n2 |
|
|
||||||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
à)A = {x R | |
√ |
3 |
−x ≥ 2}. Сначала найдем элементы это- |
|||||||||||||
|
|
|
x |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
−
го множества√ . Оно состоит из всех чисел, удовлетворяющих нера-
x − 2
венству 3 − x ≥ 2, которое, в свою очередь, равносильно нера-
x − 2
венству 3 − x ≥ 4. Решим последнее неравенство:
x − 2 |
≥ |
4 |
|
|
x − 2 |
|
− |
4 |
≥ |
0 |
|
5x − 14 |
≥ |
0 |
|
|||||||||||
3 |
− |
x |
|
3 |
− |
x |
|
|
3 |
− |
x |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
5x − |
14 |
≤ |
0 |
|
x |
|
[14=5; 3) : |
|
|
||||||||||||
|
|
|
|
|
x |
− |
3 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Èòàê, A = [14=5; 3). Это множество ограничено (и сверху, и снизу), обладает наименьшим элементом (min A = 14=5), max A
не существует, inf A = 14=5, sup A = 3. |
|
|
|
|
|
|
||||||||||||
á) A = |
{x I | 24 x2 |
≤ |
1 |
}. Это множество состоит из всех |
||||||||||||||
16 |
||||||||||||||||||
иррациональных чисел, удовлетворяющих неравенству |
|
|||||||||||||||||
24 x2 |
≤ |
1 |
, которое, в свою очередь, равносильно неравенству |
|||||||||||||||
16 |
||||||||||||||||||
24 x2 |
≤ 2 4. Решим последнее неравенство: |
|
√ |
|
|
|||||||||||||
24 x2 |
2 4 |
|
4 |
− |
x2 |
4 |
x2 |
≥ |
8 |
x |
|
|
||||||
8 |
||||||||||||||||||
|
≤ |
|
|
|
|
≤ − |
|
|
| | ≥ |
|
|
|||||||
√√
x ≤ − 8 èëè x ≥ 8 :
29

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
A = I ∩ (−∞; − 8] [ |
|
|
8; +∞) . Это множество не ограни- |
|||||||||||||||||||||||||||||||||||||||||||||||||||
÷åíî íè |
сверху, ни снизу, не обладает крайними элементами, |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
inf A = −∞, sup A = +∞. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
á') A = {x I | 24 x2 ≥ |
1 |
|
}. Это множество состоит из всех |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
16 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
иррациональных чисел, удовлетворяющих неравенству |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
24 x2 ≥ |
1 |
|
, которое, в свою очередь, равносильно неравенству |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
16 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
24 x2 ≥ 2 4. Решим последнее неравенство: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
24 x2 ≥ 2 4 4 − x2 ≥ −4 x2 ≤ 8 |x| ≤ √ |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
8 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
( √ |
|
√ |
|
|
|
− 8 ≤ x ≤ |
8 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
A = I ∩ [− |
8; 8] . Это множество ограни÷åíî è ñâåðõó, è |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
снизу, обладает крайними элементами, т.к. |
− |
√ |
8 I |
è |
|
√ |
I |
, |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
, |
max A = sup A = √ |
|
|
. |
|
|
|
|
|
8 |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
= |
|
8 |
8 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
min A = inf A 2 |
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
â) A = { |
4n − 3 |
| n N} : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
5n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
Множество A состоит из чисел вида |
|
4n2 − 3 |
|
|
|
n |
|
N. |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
4n2 − 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5n2 |
|
, ãäå |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
> 0 ïðè âñåõ n |
|
|
N è |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
5n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
4n2 − 3 |
|
|
= |
4n2 |
|
|
|
|
|
|
3 |
= |
4 |
|
|
3 |
|
|
< |
4 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
5n2 − |
|
5n2 |
|
− 5n2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
5n2 |
|
|
|
|
5 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
ïðè âñåõ n N. Следовательно, A - ограничено. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
Покажем, что min A = 1=5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
Так как элементы множества A представимы формулой |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
4 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
− |
|
, то первый элемент множества A, т.е. элемент при n = 1, |
||||||||||||||||||||||||||||||||||||||||||||||||||||
5 |
5n2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
равен 1=5, а при увеличении n, значение выражения |
|
4 |
− |
|
3 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
5 |
|
5n2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
также увеличивается (т.к. мы отнимаем все меньшее число из 4=5). Следовательно, min A = 1=5.
Докажем, что max A не существует.
От противного. Пусть множество A обладаем наибольшим элементом, тогда он достигается при некотором значении
30

n0 N, ò.å. max A = |
4 |
− |
3 |
4 |
− |
3 |
> |
4 |
− |
3 |
|
||||||||
|
|
|
|
|
|
|
|
||||||||||||
5 |
5n02 . Íî 5 |
5(n0 + 1)2 |
5 |
5n02 |
|||||||||||||||
è |
( |
5 |
− 5(n0 |
+ 1)2 ) |
A, т.е. мы нашли элемент множества A, |
||||||||||||||
|
|
4 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
больший максимального. Полученное противоречие доказывает, что наше предположение неверно и, следовательно, max A íå ñó-
ществует.
Найдем нижнюю и верхнюю грани множества A. Так как минимальный элемент множества A существует и равен 1=5, то нижняя грань множества также равна числу 1=5, ò.å.
inf A = min A = 1=5. Докажем, что sup A = 4=5.
Во-первых, выше мы видели, что число 4=5 является верхней границей множества A, т.к. 4/5 больше любого элемента множества A. Во-вторых, для любого положительного числа " число 4=5 − " уже не является верхней границей множества A, ò.ê. ñó-
4 3
ществует элемент a множества A (т.е. элемент вида 5 − 5n2 )
такой, что
a > 4=5 − " каково бы ни было положительное число ". Действительно, можно подобрать такое натуральное число n, что выпол-
нится неравенство |
4 |
− |
3 |
> |
4 |
− ", поскольку оно равносильно |
||||||||
|
|
|
||||||||||||
5 |
5n2 |
5 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
неравенству |
3 |
< " |
5n2 |
> |
3 |
n2 > |
3 |
n > √ |
3 |
|
||||
|
|
|
|
|
||||||||||
5n2 |
" |
5" |
5" |
|
||||||||||
(в силу принципа Архимеда всегда можно найти натуральное число, большее любого наперед заданного).
Итак, множество A ограничено и сверху, и снизу; обладает наименьшим элементом, min A = 1=5, но не обладает наибольшим элементом; inf A = min A = 1=5, à sup A = 4=5.
31
