Метода Румянцев

женной ниже прямой (6.33), функция F1 (x1 , x2 ) = 2x1 + 4x2 − 440 принимает отрицательные значения, на другой, расположенной выше прямой (6.33), – положительные. Таким образом, первое из неравенств (6.30) выполняется на множестве точек, которое включает в себя прямую (6.33) и полуплоскость, расположенную ниже этой прямой. На рис. 6.10 соответствующая часть плоскости заштрихована.

Совершенно аналогично можно найти множества точек, удовлетворяющих второму и третьему неравенствам из системы (6.30). Они показаны на рис. 6.11, 6.12 штриховкой.

x1

2x1 + 2,5x2 = 320

Рис. 6.12. Решение неравенства 2x1 + 2,5x2 ≤ 320

Возьмем пересечение трех найденных множеств и выделим его часть, расположенную в первой четверти. В результате получим множество точек, удовлетворяющих всей совокупности ограничений (6.30), (6.31). Данное множество имеет вид пятиугольника, показанного на рис. 6.13. Его вершинами являются точки пересечения прямых, на которых неравенства (6.30), (6.31) пере-

110

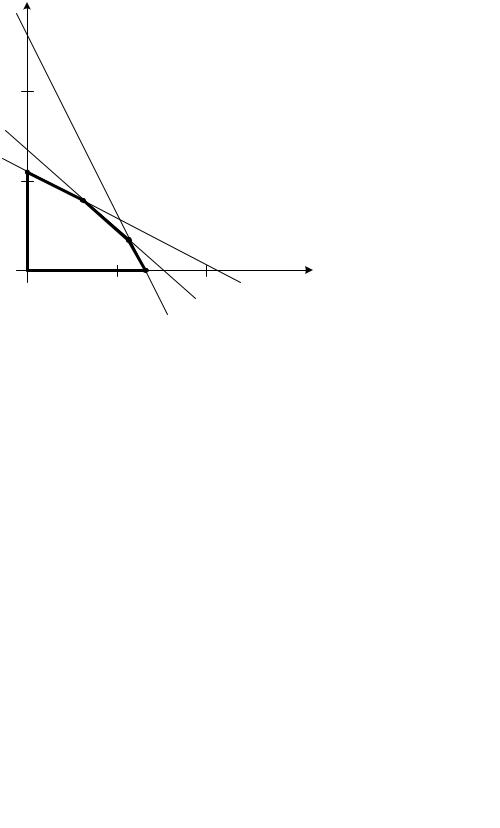
ходят в точные равенства. Координаты вершин пятиугольника указаны на рис. 6.13.

Любой точке М с целочисленными координатами ( x1 , x2 ), принадлежащей данному пятиугольнику, соответствует план выпуска стульев, который может быть выполнен при имеющихся запасах сырья и трудовых ресурсов (реализуемый план). Наоборот, если точка М не принадлежит пятиугольнику, то соответствующий план не может быть выполнен (нереализуемый план).

Рассмотрим на плоскости x1 , x2 линии

Уравнение (6.34) описывает семейство прямых, параллельных прямой

При параллельном переносе этой прямой вверх параметр С возрастает, при переносе вниз – убывает.

Свойства функции (6.32) тесно связаны с прямыми (6.34). Вдоль каждой из них она сохраняет постоянное значение равное С, а при переходе с одной прямой на другую ее значение меняется. Иными словами, прямые (6.34) – это линии уровня функции (6.32). Значение функции вдоль линии уровня (6.34) тем больше, чем больше число С, т. е. чем дальше от начала координат расположена эта линия. Отсюда следует важный вывод: оптимальный план должен располагаться на прямой семейства (6.34), наиболее удаленной от начала координат.

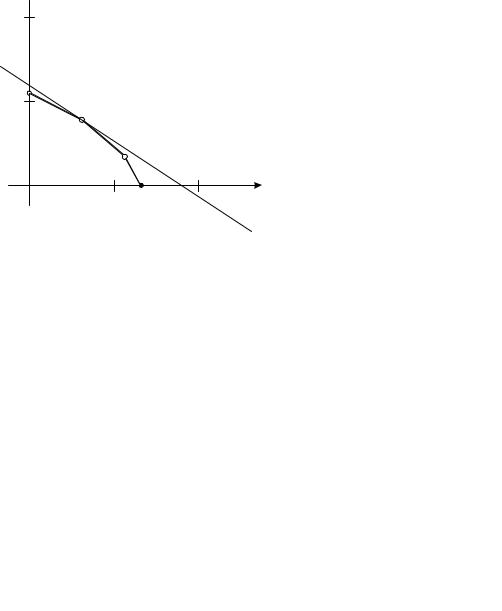
Этот вывод позволяет закончить решение задачи. Посмотрите на рис. 6.14. На нем воспроизведен пятиугольник реализуемых планов и проведена прямая

семейства (6.34), проходящая через точку M 2 с координатами (60,80). Она является предельной прямой семейства, имеющей общую точку с пятиугольником.

111

x2

Рис. 6.14. Определение оптимального плана производства стульев

Итак, оптимальный план найден. Он предписывает производить 60 стульев первого типа и 80 стульев второго типа. Стоимость этой продукции 72000 р. На выполнение данного плана нужно затратить: 440 м досок, 50 м2 обивочной ткани, 320 чел./ч рабочего времени. Оптимальный план требует полного использования запаса досок и трудовых ресурсов, в то время как обивочная ткань будет израсходована не полностью – останется 15 м2.

Последний вывод ясен из рис. 6.14. Точка M 2 , определяющая оптимальный план, является вершиной пятиугольника, лежащей на пересечении прямых

Уравнения прямых (6.36) получаются из первого и третьего условий системы (6.30) при замене их на строгие равенства. Это означает полный расход досок и

трудовых ресурсов. Однако точка M 2 лежит ниже прямой

0,5x1 + 0,25x2 = 65,

так что второе условие системы (6.30), связанное с ограниченностью запаса ткани, имеет в ней форму неравенства 50 < 65.

Проведенный анализ показывает, что дальнейшее увеличение стоимости продукции регламентируется запасом досок и трудовыми ресурсами.

В заключение сделаем несколько замечаний.

1. При практическом решении подобных задач вовсе не обязательно строить прямые семейства (6.34), как на рис. 6.14. Достаточно вычислить значения целевой функции (6.32) в точках пересечения прямых, ограничивающих ОДЗП (в рассмотренном случае это точки M1 , M 2 , M 3 , M 4 ) и выбрать среди них

точку, в которой это значение максимально.

2. Если координаты точек пересечения получились дробными, задача решается точно так же, только в окончательном решении отбрасываются дробные части полученных значений параметров оптимизации.

112

3. Если в двух соседних точках (например, M 2 , M 3 ) значения целевой функции оказались одинаковыми, это значит, что отрезок M 2 M 3 лежит на од-

ной линии уровня. В качестве решения задачи может быть выбрана любая точка этого отрезка, имеющая целочисленные координаты. Если точек с целочисленными координатами на отрезке нет, выбирают любую точку, в которой округление, вызванное отбрасыванием дробных частей, приводит к меньшему изменению значений параметров. (Таких точек может быть несколько.)

***

Мы рассмотрели две задачи линейного программирования. Небольшое количество переменных (4 маршрута и 2 вида продукции) позволило просто и наглядно получить их решение.

В настоящее время разработано большое количество компьютерных программ, реализующих общие алгоритмы решения задач линейного программирования для практически неограниченного количества параметров. Использование вычислительной техники при решении задач линейного программирования послужило основой широкого применения математических методов в экономике.

§5. Общие рекомендации. Что и как оптимизировать?

Мы познакомились с постановкой задач оптимизации и рассмотрели ряд способов минимизации функций (именно к этому сводится математическая сторона вопроса). Нами охвачена лишь небольшая часть известных методов решения подобных задач. Вместо дальнейшего изучения методов обратим внимание на другие, не менее важные вопросы.

Решение задач оптимизации состоит из следующих этапов:

1.Создание математической модели явления (объекта, процесса).

2.Определение целевой функции и важнейших параметров, подлежащих оптимизации.

3.Непосредственная минимизация некоторой функции (обычно большого числа переменных).

4.Внедрение результатов исследования.

Было бы ошибочно считать, что первые три из них относятся к исключительной компетенции математиков, и лишь на последнем этапе должны подключаться специалисты конкретной отрасли. Участие этих специалистов крайне необходимо и на первом, и особенно на втором этапе. В противном случае возможны серьезные просчеты. Н.С. Бахвалов описывает такую реально произошедшую ситуацию (Бахвалов Н.С. Численные методы. – М.: Наука, 1973. – 631с.):

«Производство сахара складывается из следующих этапов: выращивание сахарной свеклы, транспортировка, переработка на заводах. Математики, поставившие перед собой задачу оптимизировать производство сахарной свеклы, в первую очередь решили заняться минимизацией транспортных расходов. Эта задача была успешно решена, но хозяйственные руководители отказались принять полученный план перевозок к действию. Основой послу-

113

жил довод о том, что при оптимизации транспортировки свеклы ухудшались условия транспортировки других сельскохозяйственных культур, а также усложнялась организация переработки: некоторые заводы оказывались перегруженными, другие недогруженными.

За этими возражениями стояли такие соображения. Себестоимость сахара складывается из следующих составляющих (числа условные):

80% – стоимость сахарной свеклы,

5% – транспортные расходы,

15% – расходы по переработке.

Ожидаемая экономия от минимизации транспортных расходов составляет 10% этих расходов, т.е. всего 0,5% себестоимости сахара. В то же время эта перестройка требует больших хлопот и неизвестно, не произойдет ли более существенных потерь за счет каких-то неучтенных моментов.

Из описанной выше структуры себестоимости видно, что за счет оптимизации расходов по транспортировке и переработке трудно достигнуть существенного повышения эффективности. Внимательный анализ проблемы позволил обнаружить следующее обстоятельство. Выход сахара из тонны свеклы пропорционален ее сахаристости, которая изменяется по определенному закону в процессе созревания и падает в процессе хранения. В частности, при позднем начале уборки происходят большие потери из-за того, что на сахарные заводы поступает одновременно большое количество свеклы, и она там долго хранится.

В результате этого анализа была поставлена новая цель – оптимизация выхода сахара (при заданном оборудовании) и построена математическая модель, учитывающая изменение сахаристости в процессе копки и хранения свеклы.

Дальнейший анализ показал, что и эта модель обладает определенным дефектом. При оптимальном (согласно этой модели) графике работы копка должна начинаться, когда свекла еще находится в стадии интенсивного роста, что экономически невыгодно для непосредственных производителей. Для преодоления этого противоречия потребовалось, чтобы модель учитывала вопросы экономической заинтересованности производителей.»

Описанный случай весьма поучителен и позволяет сделать ряд полезных выводов.

Во-первых, никогда не следует браться за первую попавшуюся задачу только потому, что хорошо умеешь ее решать. Следует рассмотреть явление со всех сторон, выявить те факторы, которые оказывают наибольшее влияние на интересующий нас результат, и оптимизировать, в первую очередь, именно эти факторы. Если мы ставим целью снизить себестоимость чего-либо, то в первую очередь надо оптимизировать самую дорогостоящую операцию.

Во-вторых, улучшая что-то одно, мы неизбежно ухудшаем что-то другое. Поэтому, ставя задачу оптимизации, надо учитывать не только локальный выигрыш, но и все возможные проигрыши. Например, удешевление производства или строительства может привести к некоторому снижению качества, что потребует более частых ремонтов. В результате эксплуатация таких «более дешевых» изделий или объектов обойдется дороже.

В-третьих, оптимальные производственные планы или графики работ часто оказываются невыгодными для отдельных участников общей работы. Например, оптимизация транспортных расходов неизбежно снижает доходы транспортников. Поэтому результатом решения оптимизационной задачи должен быть не только производственный план или график работ, но и рекомендации по наилучшей организации оплаты труда и ценовой политике.

114

Сергей Алексеевич Румянцев

Основы математического моделирования и вычислительной математики

Курс лекций для студентов технических специальностей и инженеров

Редактор С.В. Пилюгина

620034, Екатеринбург, ул. Колмогорова, 66, УрГУПС Редакционно-издательский отдел

115