
Методичка по лабе Механики
.pdf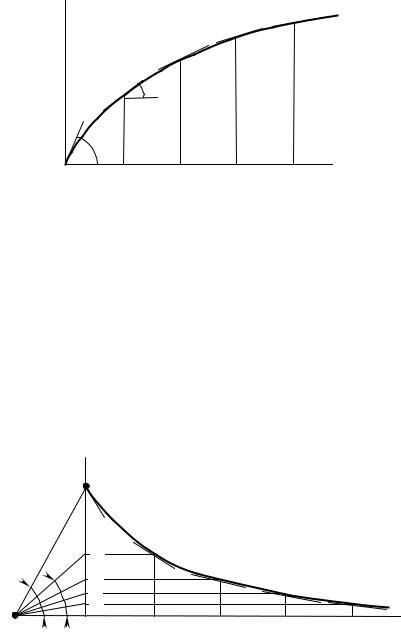
S |
|
|
A3 |
A4 |
|
|
A2 |
|
|
|
|
|
|
|
|
A1 |
Į1 |
|
|
|
Į0 |
|
|
t |
Ɉ |
A0 |
t2 |
t3 |
|
t1 |
t4 |
Ɋɢɫɭɧɨɤ 5.2 – Ƚɪɚɮɢɤ ɞɜɢɠɟɧɢɹ ɬɨɱɤɢ
Ɉɬɤɥɚɞɵɜɚɸɬ ɨɬ ɧɚɱɚɥɚ ɨɫɟɣ ɤɨɨɪɞɢɧɚɬ ȣO1t (ɪɢɫ. 5.3) ɨɬɪɟɡɨɤ Ɉ1Ʉ1,
ɪɚɜɧɵɣ ɟɞɢɧɢɰɟ ɜɪɟɦɟɧɢ ɜ ɩɪɢɧɹɬɨɦ ɦɚɫɲɬɚɛɟ, ɢ ɢɡ ɬɨɱɤɢ Ʉ1 ɩɪɨɜɨɞɹɬ ɩɪɹ-
ɦɵɟ, ɩɚɪɚɥɥɟɥɶɧɵɟ ɤɚɫɚɬɟɥɶɧɵɦ ɤ ɝɪɚɮɢɤɭ ɞɜɢɠɟɧɢɹ ɜ ɬɨɱɤɚɯ Ⱥ0, Ⱥ1, Ⱥ2,... ɞɨ ɩɟɪɟɫɟɱɟɧɢɹ ɫ ɨɫɶɸ ɨɪɞɢɧɚɬ. Ɉɬɪɟɡɤɢ, ɨɬɫɟɤɚɟɦɵɟ ɷɬɢɦɢ ɩɪɹɦɵɦɢ, ɧɚ ɨɫɢ
O1ȣ ɞɚɞɭɬ ɜ ɫɨɨɬɜɟɬɫɬɜɭɸɳɟɦ ɦɚɫɲɬɚɛɟ ɚɥɝɟɛɪɚɢɱɟɫɤɢɟ ɡɧɚɱɟɧɢɹ ɫɤɨɪɨɫɬɢ
ɬɨɱɤɢ ɜ ɦɨɦɟɧɬɵ t0 = 0, t1, t2, ...
|
|
ȣ |
|
|
|
|
ȣ0 ȼ0 |
|
|
|
Į1 |
ȣ1 |
ȼ1 |
|
Į0 |
ȼ2 |
|
||
ȣ2 |
|
|||
|
|
ȼ3 |
|
|
|
|
ȣ3 |
ȼ4 |
Ʉ1 |
ȣ4 |
t1 |
t2 |
t3 |
t |
|
Ɉ1 |
||||||
t4 |
Ɋɢɫɭɧɨɤ 5.3 – Ƚɪɚɮɢɤ ɫɤɨɪɨɫɬɢ ɬɨɱɤɢ
Ⱦɟɣɫɬɜɢɬɟɥɶɧɨ, ɧɚ ɪɢɫ. 5.3:
~ |
~ |
, tgĮ2 |
~ |
tgĮ0 X0, tgĮ1 |
X1 |
X2 ... |
|
|
ɉɪɢ O1K1 = 1 ɩɨɥɭɱɚɟɦ O1ȣ0 = Ɉ1K1 tgĮ0 = tgĮ0, O1ȣ1= tgĮ1, O1ȣ2 = tgĮ2,... |
|
|
ȼɨɫɫɬɚɜɢɜ ɩɟɪɩɟɧɞɢɤɭɥɹɪɵ ɤ ɨɫɢ t ɜ ɬɨɱɤɚɯ t1, t2, t3,... ɢ ɤ ɨɫɢ ȣ ɜ ɬɨɱɤɚɯ |
~ |
~ |
~ |
X1 |
, X2 |
, X3 ... , ɩɨɥɭɱɢɦ ɬɨɱɤɢ ȼ1, ȼ2, ȼ3,... ɝɪɚɮɢɤɚ ɫɤɨɪɨɫɬɢ. |
|
|
Ɇɚɫɲɬɚɛ ɫɤɨɪɨɫɬɢ ȝȣ, ɦ·ɪɚɞ–1/ɦɦ, ɨɩɪɟɞɟɥɹɟɬɫɹ ɩɨ ɮɨɪɦɭɥɟ |
11

ȝX |
ȝS |
|
, |
(5.3) |
||
|
|
|||||
|
ȝ |
M |
k |
|
||
|
|
|
1 |
|
|
|
ɝɞɟ k1 – ɪɚɫɫɬɨɹɧɢɟ Ɉ1Ʉ1 ɧɚ ɞɢɚɝɪɚɦɦɟ ɫɤɨɪɨɫɬɢ, ɦɦ.
5.3 ɉɨɫɬɪɨɟɧɢɟ ɞɢɚɝɪɚɦɦɵ ɭɫɤɨɪɟɧɢɹ
Ƚɪɚɮɢɤ ɭɫɤɨɪɟɧɢɹ ɫɬɪɨɹɬ ɚɧɚɥɨɝɢɱɧɨ.
Ɉɬɥɨɠɢɜ ɨɬ ɧɚɱɚɥɚ ɨɫɟɣ a02t ɨɬɪɟɡɨɤ 02K2, ɪɚɜɧɵɣ ɟɞɢɧɢɰɟ ɜɪɟɦɟɧɢ ɜ ɩɪɢɧɹɬɨɦ ɦɚɫɲɬɚɛɟ (ɪɢɫ. 5.4), ɩɪɨɜɨɞɢɦ ɢɡ ɬɨɱɤɢ K2 ɩɪɹɦɵɟ, ɩɚɪɚɥɥɟɥɶɧɵɟ ɤɚɫɚɬɟɥɶɧɵɦ ɤ ɝɪɚɮɢɤɭ ɫɤɨɪɨɫɬɢ ɜ ɬɨɱɤɚɯ ȼ1, ȼ2, ȼ3,…
Ɉɬɪɟɡɤɢ, ɨɬɫɟɤɚɟɦɵɟ ɷɬɢɦɢ ɩɪɹɦɵɦɢ ɧɚ ɨɫɢ 02ɚ, ɨɩɪɟɞɟɥɹɸɬ ɜ ɫɨɨɬɜɟɬ-
ɫɬɜɭɸɳɟɦ ɦɚɫɲɬɚɛɟ ɚɥɝɟɛɪɚɢɱɟɫɤɢɟ ɡɧɚɱɟɧɢɹ ɤɚɫɚɬɟɥɶɧɵɯ ɭɫɤɨɪɟɧɢɣ ɬɨɱɤɢ ɜ ɦɨɦɟɧɬɵ t0 = 0, t1, t2, t3, ...
ȼɨɫɫɬɚɜɢɜ ɩɟɪɩɟɧɞɢɤɭɥɹɪɵ ɤ ɨɫɢ t ɜ ɬɨɱɤɚɯ t1, t2, t3 …ɢ ɤ ɨɫɢ ɚ ɜ ɬɨɱɤɚɯ a1, a2, a3, …, ɩɨɥɭɱɢɦ ɬɨɱɤɢ ɋ1, ɋ2, ɋ3, ... ɝɪɚɮɢɤɚ ɤɚɫɚɬɟɥɶɧɨɝɨ ɭɫɤɨɪɟɧɢɹ.
|
ɚ |
|
|
|
|
|
K2 |
Ɉ2 |
t1 |
t2 |
t3 |
t4 |
t |
|
|
ɚɚ24 ɚ3 |
|
|
|
|
|
|
ɋ2 |
ɋ3 |
ɋ4 |
|
|
|
|
ɚ1 |
|
|
ɋ1
ɚ0 ɋ0
Ɋɢɫɭɧɨɤ 5.4 – Ƚɪɚɮɢɤ ɭɫɤɨɪɟɧɢɹ ɬɨɱɤɢ
Ɇɚɫɲɬɚɛ ɭɫɤɨɪɟɧɢɹ ȝɚ, ɦ·ɪɚɞ–2/ɦɦ, ɨɩɪɟɞɟɥɹɟɬɫɹ ɩɨ ɮɨɪɦɭɥɟ
ȝ |
ɚ |
ȝX |
|
|
|
ȝS |
|
, |
(5.4) |
|||
ȝ |
|
k |
2 |
|
ȝ |
|
k k |
2 |
||||
|
|
|
M |
|
|
|
M |
1 |
|
|
||
ɝɞɟ k2 – ɪɚɫɫɬɨɹɧɢɟ Ɉ2K2 ɧɚ ɞɢɚɝɪɚɦɦɟ ɭɫɤɨɪɟɧɢɹ, ɦɦ.
ɉɨɫɬɪɨɟɧɢɟ ɝɪɚɮɢɤɨɜ ɫɤɨɪɨɫɬɢ ɢ ɭɫɤɨɪɟɧɢɹ ɩɨ ɡɚɞɚɧɧɨɦɭ ɝɪɚɮɢɤɭ ɞɜɢɠɟɧɢɹ, ɨɫɧɨɜɚɧɧɨɟ ɧɚ ɡɚɜɢɫɢɦɨɫɬɹɯ
12
~ |
ds |
~ |
~ |
|
dX |
||||
X |
|
, a |
|
|
dt |
dt |
|||
|
|
ɹɜɥɹɟɬɫɹ ɦɟɬɨɞɨɦ ɝɪɚɮɢɱɟɫɤɨɝɨ ɞɢɮɮɟɪɟɧɰɢɪɨɜɚɧɢɹ.
Ɍɚɤ ɤɚɤ ɤɪɢɜɨɲɢɩ ɜɪɚɳɚɟɬɫɹ ɫ ɩɨɫɬɨɹɧɧɨɣ ɭɝɥɨɜɨɣ ɫɤɨɪɨɫɬɶɸ Ȧ2, ɬɨ ɦɨɠɧɨ ɫɱɢɬɚɬɶ, ɱɬɨ ɩɨ ɨɫɢ ɚɛɫɰɢɫɫ ɨɬɤɥɚɞɵɜɚɟɬɫɹ ɧɟ ɜɪɟɦɹ t, ɚ ɭɝɥɵ ɩɨɜɨɪɨɬɚ
ij2 ɡɜɟɧɚ 2, ɬɨ ɟɫɬɶ ɞɢɚɝɪɚɦɦɵ sɋ = sɋ (t), ȣɋ = ȣɋ (t), aɋ = aɋ(t) ɛɭɞɭɬ ɨɞɧɨɜɪɟɦɟɧɧɨ ɢ ɞɢɚɝɪɚɦɦɚɦɢ sɋ = sɋ (ij2), ȣɋ = ȣɋ (ij2), aɋ = aɋ(ij2).
Ɍɚɤɚɹ ɦɟɬɨɞɢɤɚ ɩɨɫɬɪɨɟɧɢɹ ɤɢɧɟɦɚɬɢɱɟɫɤɢɯ ɞɢɚɝɪɚɦɦ ɦɨɠɟɬ ɛɵɬɶ ɩɪɢɦɟɧɟɧɚ ɞɥɹ ɥɸɛɵɯ ɩɥɨɫɤɢɯ ɦɟɯɚɧɢɡɦɨɜ, ɤɚɤ ɫ ɧɢɡɲɢɦɢ, ɬɚɤ ɢ ɫ ɜɵɫɲɢɦɢ ɤɢɧɟɦɚɬɢɱɟɫɤɢɦɢ ɩɚɪɚɦɢ.
5.4 Ɋɟɡɭɥɶɬɚɬɵ ɝɪɚɮɢɱɟɫɤɢɯ ɪɚɫɱɟɬɨɜ ɡɚɧɨɫɹɬɫɹ ɜ ɬɚɛɥɢɰɭ 5.2. ɑɢɫɥɟɧ-
ɧɵɟ ɡɧɚɱɟɧɢɹ ɩɟɪɟɦɟɳɟɧɢɣ, ɫɤɨɪɨɫɬɟɣ ɢ ɭɫɤɨɪɟɧɢɣ ɨɩɪɟɞɟɥɹɸɬɫɹ ɩɨ ɮɨɪɦɭ-
ɥɚɦ
S yȝS |
, X y ȝX , a |
y ȝa , |
(5.5) |
|
c |
cc |
|
ɝɞɟ y, y', y'' – ɨɪɞɢɧɚɬɵ ɢɫɫɥɟɞɭɟɦɨɣ ɬɨɱɤɢ ɧɚ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɯ ɝɪɚɮɢɤɚɯ ɩɟ-
ɪɟɦɟɳɟɧɢɣ, ɫɤɨɪɨɫɬɢ ɢ ɭɫɤɨɪɟɧɢɹ, ɦɦ.
ɉɪɢ ɫɨɫɬɚɜɥɟɧɢɢ ɬɚɛɥɢɰ ɧɟɨɛɯɨɞɢɦɨ ɭɱɢɬɵɜɚɬɶ ɡɧɚɤ ɤɢɧɟɦɚɬɢɱɟɫɤɢɯ ɜɟɥɢɱɢɧ (ɩɨ ɞɢɚɝɪɚɦɦɚɦ).
13
|
|
|
|
|
|
|
|
|
Ɍɚɛɥɢɰɚ 5.2 |
|
|
|
|
|
Ɋɟɡɭɥɶɬɚɬɵ ɪɚɫɱɟɬɨɜ |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
ij,˚ |
|
S |
|
|
ȣ |
|
a |
|||
|
y, ɦɦ |
|
S, ɦ |
|
y', ɦɦ |
|
ȣ,ɦ/ɪɚɞ |
y'', ɦɦ |
|
a, ɦ/ɪɚɞ2 |
0 |
|
|
|
|
|
|
|
|
|
|
30 |
|
|
|
|
|
|
|
|
|
|
60 |
|
|
|
|
|
|
|
|
|
|
90 |
|
|
|
|
|
|
|
|
|
|
120 |
|
|
|
|
|
|
|
|
|
|
150 |
|
|
|
|
|
|
|
|
|
|
180 |
|
|
|
|
|
|
|
|
|
|
210 |
|
|
|
|
|
|
|
|
|
|
240 |
|
|
|
|
|
|
|
|
|
|
270 |
|
|
|
|
|
|
|
|
|
|
300 |
|
|
|
|
|
|
|
|
|
|
330 |
|
|
|
|
|
|
|
|
|
|
360 |
|
|
|
|
|
|
|
|
|
|
6 ɋɈȾȿɊɀȺɇɂȿ ɈɌɑȿɌȺ
6.1Ɉɬɱɟɬ ɨɮɨɪɦɥɹɟɬɫɹ ɧɚ ɱɟɬɵɪɟɯ ɫɬɪɚɧɢɰɚɯ ɮɨɪɦɚɬɚ Ⱥ4.
6.2ɇɚ ɫɬɪ. 1 ɩɨɦɟɳɚɟɬɫɹ ɬɢɬɭɥɶɧɵɣ ɥɢɫɬ ɫɨɝɥɚɫɧɨ ɭɫɬɚɧɨɜɥɟɧɧɨɦɭ ɨɛ-
ɪɚɡɰɭ.
6.3ɇɚ ɫɬɪ. 2 ɪɚɫɩɨɥɚɝɚɸɬɫɹ ɫɥɟɞɭɸɳɢɟ ɞɚɧɧɵɟ:
–ɰɟɥɶ ɪɚɛɨɬɵ;
–ɡɚɞɚɧɢɟ ɧɚ ɥɚɛɨɪɚɬɨɪɧɭɸ ɪɚɛɨɬɭ;
–ɧɟɨɛɯɨɞɢɦɵɟ ɩɪɢɛɨɪɵ ɢ ɦɚɬɟɪɢɚɥɵ;
–ɫɬɪɭɤɬɭɪɧɚɹ ɫɯɟɦɚ ɤɪɢɜɨɲɢɩɧɨ-ɩɨɥɡɭɧɧɨɝɨ ɦɟɯɚɧɢɡɦɚ;
–ɬɚɛɥɢɰɚ 1 (ɫɦ. ɬɚɛɥɢɰɭ 5.1) ɫ ɪɟɡɭɥɶɬɚɬɚɦɢ ɡɚɦɟɪɨɜ.
6.4ɇɚ ɫɬɪ. 3 ɪɚɫɩɨɥɚɝɚɸɬɫɹ ɫɥɟɞɭɸɳɢɟ ɞɚɧɧɵɟ:
–ɞɢɚɝɪɚɦɦɚ ɩɟɪɟɦɟɳɟɧɢɣ ɩɨɥɡɭɧɚ;
–ɞɢɚɝɪɚɦɦɚ ɫɤɨɪɨɫɬɢ ɩɨɥɡɭɧɚ;
–ɞɢɚɝɪɚɦɦɚ ɭɫɤɨɪɟɧɢɣ ɩɨɥɡɭɧɚ.
6.5ɇɚ ɫɬɪ. 4 ɪɚɫɩɨɥɚɝɚɸɬɫɹ:
–ɪɚɫɱɟɬɵ ɜɫɟɯ ɦɚɫɲɬɚɛɧɵɯ ɤɨɷɮɮɢɰɢɟɧɬɨɜ;
14

–ɬɚɛɥɢɰɚ 2 (ɫɦ. ɬɚɛɥɢɰɭ 5.2) ɫ ɪɟɡɭɥɶɬɚɬɚɦɢ ɢɡɦɟɪɟɧɢɣ ɤɢɧɟɦɚɬɢɱɟ-
ɫɤɢɯ ɜɟɥɢɱɢɧ;
–ɜɵɜɨɞɵ.
7 ɄɈɇɌɊɈɅɖɇɕȿ ȼɈɉɊɈɋɕ
1.Ʉɚɤɢɟ ɰɟɥɢ ɩɪɟɫɥɟɞɭɟɬ ɤɢɧɟɦɚɬɢɱɟɫɤɨɟ ɢɫɫɥɟɞɨɜɚɧɢɟ ɦɟɯɚɧɢɡɦɚ?
2.Ʉɚɤɢɟ ɦɟɬɨɞɵ ɤɢɧɟɦɚɬɢɱɟɫɤɨɝɨ ɢɫɫɥɟɞɨɜɚɧɢɹ ɜɵ ɡɧɚɟɬɟ?
3.ȼ ɱɟɦ ɨɬɥɢɱɢɟ ɦɟɬɨɞɚ ɩɥɚɧɨɜ ɨɬ ɦɟɬɨɞɚ ɞɢɚɝɪɚɦɦ?
4.ɇɚ ɱɬɨ ɜɥɢɹɟɬ ɜɵɛɨɪ ɜɟɥɢɱɢɧ k1 ɢ k2?
5.ȼ ɱɟɦ ɡɚɤɥɸɱɚɟɬɫɹ ɦɟɬɨɞ ɝɪɚɮɢɱɟɫɤɨɝɨ ɞɢɮɮɟɪɟɧɰɢɪɨɜɚɧɢɹ?
6.Ʉɚɤ ɢɡɦɟɧɹɬɫɹ ɝɪɚɮɢɤ ɫɤɨɪɨɫɬɢ ɢ ɫɚɦɚ ɫɤɨɪɨɫɬɶ ɬɨɱɤɢ, ɟɫɥɢ ɭɜɟɥɢɱɢɬɶ
(ɭɦɟɧɶɲɢɬɶ) ɡɧɚɱɟɧɢɟ k1?
7.ɑɬɨ ɬɚɤɨɟ «ɤɢɧɟɦɚɬɢɱɟɫɤɚɹ ɞɢɚɝɪɚɦɦɚ»?
8.Ɉɩɪɟɞɟɥɢɬɶ ɭɫɤɨɪɟɧɢɟ ɬɨɱɤɢ 1 ɝɪɚɮɢɱɟɫɤɢɦ ɫɩɨɫɨɛɨɦ:
ȣ
1
t
15
Ʌɢɬɟɪɚɬɭɪɚ
1.Ⱥɪɬɨɛɨɥɟɜɫɤɢɣ ɂ.ɂ. Ɍɟɨɪɢɹ ɦɟɯɚɧɢɡɦɨɜ ɢ ɦɚɲɢɧ: ɍɱɟɛɧ. ɞɥɹ ɜɭɡɨɜ. Ɇ. : ɇɚɭɤɚ, 1988. 604 ɫ.
2.Ɏɪɨɥɨɜ Ʉ.ȼ., ɉɨɩɨɜ ɋ.Ⱥ., Ɇɭɫɚɬɨɜ Ⱥ.Ʉ. ɢ ɞɪ. Ɍɟɨɪɢɹ ɦɟɯɚɧɢɡɦɨɜ ɢ ɦɟɯɚɧɢɤɚ ɦɚɲɢɧ: ɍɱɟɛ. ɞɥɹ ɜɭɡɨɜ. 2-ɟ ɢɡɞ., ɩɟɪɟɪɚɛ. ɢ ɞɨɩ. Ɇ. : ȼɵɫɲ. ɲɤ., 1998. 496 ɫ.
3.əɛɥɨɧɫɤɢɣ Ⱥ.Ⱥ., ɇɢɤɢɮɨɪɨɜɚ ȼ.Ɇ. Ʉɭɪɫ ɬɟɨɪɟɬɢɱɟɫɤɨɣ ɦɟɯɚɧɢɤɢ. ɑ. 1. ɋɬɚɬɢɤɚ. Ʉɢɧɟɦɚɬɢɤɚ: ɍɱɟɛ. ɞɥɹ ɬɟɯɧ. ɜɭɡɨɜ. 6-ɟ ɢɡɞ. ɢɫɩɪ. Ɇ. : ȼɵɫɲ. ɲɤ., 1984. 343 ɫ.
16
ɍɱɟɛɧɨɟ ɢɡɞɚɧɢɟ
Ɍɚɬɶɹɧɚ Ⱥɧɚɬɨɥɶɟɜɧɚ Ⱥɧɬɪɨɩɨɜɚ
Ʉɢɧɟɦɚɬɢɱɟɫɤɢɣ ɚɧɚɥɢɡ ɦɟɯɚɧɢɡɦɨɜ ɦɟɬɨɞɨɦ ɞɢɚɝɪɚɦɦ
Ɋɭɤɨɜɨɞɫɬɜɨ ɤ ɥɚɛɨɪɚɬɨɪɧɨɣ ɪɚɛɨɬɟ ɩɨ ɤɭɪɫɭ «Ɍɟɨɪɢɹ ɦɟɯɚɧɢɡɦɨɜ ɢ ɦɚɲɢɧ»
ɞɥɹ ɫɬɭɞɟɧɬɨɜ ɜɫɟɯ ɮɨɪɦ ɨɛɭɱɟɧɢɹ ɫɩɟɰɢɚɥɶɧɨɫɬɟɣ:
190302 – ɜɚɝɨɧɵ; 190303 – ɷɥɟɤɬɪɢɱɟɫɤɢɣ ɬɪɚɧɫɩɨɪɬ ɠɟɥɟɡɧɵɯ ɞɨɪɨɝ; 220401 – ɦɟɯɚɬɪɨɧɢɤɚ
Ɋɟɞɚɤɬɨɪ Ʌ.ɋ. Ȼɚɪɵɲɧɢɤɨɜɚ
ɉɨɞɩɢɫɚɧɨ ɜ ɩɟɱɚɬɶ 19.06.2009. Ɏɨɪɦɚɬ 60×84/16 . Ȼɭɦɚɝɚ ɨɮɫɟɬɧɚɹ. ɍɫɥ.-ɩɟɱ.ɥ. 1,0.
Ɍɢɪɚɠ 200 ɷɤɡ. Ɂɚɤɚɡ 189.
ɂɡɞɚɬɟɥɶɫɬɜɨ ɍɪȽɍɉɋ 620034, ȿɤɚɬɟɪɢɧɛɭɪɝ, ɭɥ. Ʉɨɥɦɨɝɨɪɨɜɚ, 66.
Ɍɟɥ.: (343) 245-43-90.
17
