
- •Ю. И. Масленников Электромагнетизм Тестовые задания
- •Предисловие
- •1. Электрическое поле (эп)
- •1.1. Расчетные формулы по теме «эп»
- •1.2. Тестовые задания по теме «эп»
- •2. Электроемкость и конденсаторы (эк)
- •2.1. Расчетные формулы по теме «эк»
- •2.2. Тестовые задания по теме «эк»
- •3. Законы постоянного тока (зпт)
- •3.1. Расчетные формулы по теме «зпт»
- •3.2. Тестовые задания по теме зпт
- •4.Магнитное поле тока (мпт)
- •4.1. Определения основных понятий мпт
- •4.2.Основные формулы раздела «мпт»
- •4.3. Тестовые задания по теме «мпт»
- •4.4. Задачи на тему мпт
- •5. Сила Лоренца (сл)
- •5.1. Расчётные формулы
- •5.2. Тестовые задания по теме «сл»
- •6. Электромагнетизм (эм)
- •6.1. Электромагнитная индукция и самоиндукция
- •6.2. Расчетные формулы по теме «эм»
- •6.3. Тестовые задачи по теме «эм»
- •7. Электромагнитные колебания (эмк)
- •7.1. Собственные незатухающие электромагнитные колебания
- •7.2. Собственные затухающие эмк
- •7.3. Расчетные формулы по теме «эмк»
- •7.4. Расчетные формулы в задании «переменный ток»
- •7.5. Тестовые задания по теме эмк
- •8.Библиографический список
- •Электромагнетизм Тестовые задания
- •620034, Екатеринбург, ул. Колмогорова, 66 Приложение
- •Приложение
7. Электромагнитные колебания (эмк)
7.1. Собственные незатухающие электромагнитные колебания
1.
Контур LC.
Электромагнитный колебательный контур
(ЭМК) состоит из конденсатора емкостью
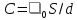 с емкостным сопротивлением
с емкостным сопротивлением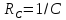 и катушки индуктивностью
и катушки индуктивностью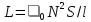 ,
индуктивным сопротивлением
,
индуктивным сопротивлением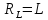 ,
где
– относительная диэлектрическая
проницаемость среды,
− относительная магнитная проницаемость
среды,
−
циклическая частота,
,
где
– относительная диэлектрическая
проницаемость среды,
− относительная магнитная проницаемость
среды,
−
циклическая частота,
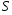 −
площадь, d
− расстояние между пластинами
конденсатора, N
–
число витков в катушке. Максимальная
энергия электрического (э) поля в
конденсаторе
−
площадь, d
− расстояние между пластинами
конденсатора, N
–
число витков в катушке. Максимальная
энергия электрического (э) поля в
конденсаторе
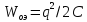 ,
максимальная энергия магнитного (м)
поля в катушке
,
максимальная энергия магнитного (м)
поля в катушке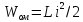 .
В любой момент времени суммарная энергия
.
В любой момент времени суммарная энергия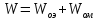 .
При удельном сопротивлении
.
При удельном сопротивлении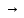 0
убыль энергии
0
убыль энергии
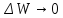 ,
отсюда
,
отсюда
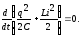
Учитывая,
что сила тока
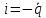 ,
а производная
,
а производная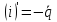 ,
запишем дифференциальное уравнение
,
запишем дифференциальное уравнение
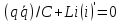 ;
;
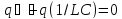 .
.
Решением дифференциального уравнения является функция
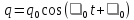 ,
,
где циклическая частота 0 = 2/Т0; 1/LC = 02.
В
ЭМК изменяются по гармоническому закону:
в конденсаторе
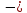 зарядq,
напряжение U,
напряженность электрического поля E,
плотность энергии электрического поля
зарядq,
напряжение U,
напряженность электрического поля E,
плотность энергии электрического поля
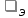 ,
энергия электрического поляWэ,
поверхностная плотность заряда ;
в катушке
,
энергия электрического поляWэ,
поверхностная плотность заряда ;
в катушке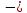 магнитный поток Ф, индукция магнитного
поляB,
напряженность магнитного поля H,
сила тока i,
плотность энергии магнитного поля М,
энергия магнитного поля
магнитный поток Ф, индукция магнитного
поляB,
напряженность магнитного поля H,
сила тока i,
плотность энергии магнитного поля М,
энергия магнитного поля
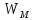 ,
ЭДС самоиндукции
,
ЭДС самоиндукции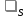 .
.
Ниже приведены соответствующие формулы:
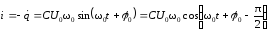 ,
,
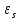
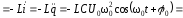
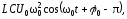
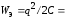
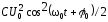 ,
,
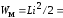
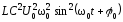 /
2.
/
2.
При
условии
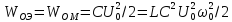 ,
получим
,
получим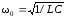 .
.
В
ЭМК заряд q
опережает силу тока i
по фазе на
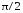 ,
а ЭДС самоиндукции
,
а ЭДС самоиндукции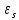 –
на π, сила тока i
опережает ЭДС самоиндукции
–
на π, сила тока i
опережает ЭДС самоиндукции
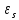 по фазе на π/2.
по фазе на π/2.
2. Контуры C; L; RLC в цепи переменного напряжения.
а)
На емкость
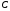 подано переменное напряжение
подано переменное напряжение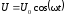 .
.
При
t0
=
0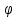 0
=
0;
R
= 0,
L
= 0.
В цепи сила тока
0
=
0;
R
= 0,
L
= 0.
В цепи сила тока
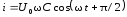 опережает
напряжение по фазе на
опережает
напряжение по фазе на
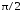 .
.
б)
На индуктивность
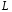 подано напряжение
подано напряжение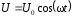 .
.
При
t0
=
0
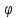 0
=
0;
R
= 0,
C
= 0.
В цепи сила тока
0
=
0;
R
= 0,
C
= 0.
В цепи сила тока
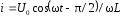 отстает от напряжения по фазе на
отстает от напряжения по фазе на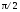 .
.
в)
На контур
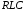 подано напряжение
подано напряжение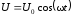 .
При условии
.
При условии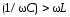 сила тока опережает напряжение по фазе
сила тока опережает напряжение по фазе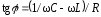 ,
а общее сопротивление цепи (импеданс)
,
а общее сопротивление цепи (импеданс)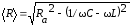 .
.
Закон
Ома
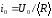 .
.
Резонанс
напряжения. При
условии
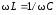 сдвиг фазыtg
φ
=0.
сдвиг фазыtg
φ
=0.
Ток
и напряжение совпадают по фазе. Сила
тока
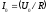 .
.
Активная мощность 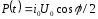 , реактивная мощность
, реактивная мощность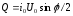 ,
действующее значение напряжения
,
действующее значение напряжения
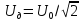 ,
действующее значение силы тока
,
действующее значение силы тока
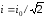 ,
определяемое по тепловому эффекту.
,
определяемое по тепловому эффекту.
7.2. Собственные затухающие эмк
При удельном сопротивлении ρ≠ 0 убыль энергии в контуре RLC равна джоулевой теплоте:

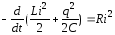 .
.
При
известном условии
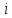 = –
= –
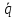 ,
,
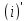 = –
= –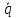 запишем дифференциальное уравнение:
запишем дифференциальное уравнение:
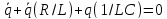 ,
,
где R/L = 2β, 1/LC = ω02. Решением дифференциального уравнения
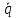 +
+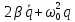 =
0
является функция
=
0
является функция
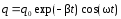 .
.
Затухающие
колебания характеризуются коэффициентом
затухания
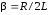 ,
циклической
частотой,
ω
=
,
циклической
частотой,
ω
=
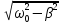 логарифмическим декрементом затухания
логарифмическим декрементом затухания
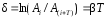 ,
добротностью
,
добротностью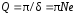 ,
временем релаксации
,
временем релаксации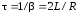 ,
в течение которого амплитуда колебаний
уменьшится вe
раз
(A1/Ai=
e),
волновым сопротивлением
~
,
в течение которого амплитуда колебаний
уменьшится вe
раз
(A1/Ai=
e),
волновым сопротивлением
~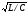 .
При значениях
<
Ra
добротность
контура Q
.
При значениях
<
Ra
добротность
контура Q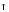 ,
число колебаний за время релаксации
Ne
,
число колебаний за время релаксации
Ne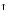 и
наоборот при
>Ra
, следует Q
и
наоборот при
>Ra
, следует Q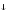 ,
число колебаний за время релаксации
Ne
↓,
τ↓.
,
число колебаний за время релаксации
Ne
↓,
τ↓.
