
Discrete.Math.in.Computer.Science,2002
.pdf
130 |
CHAPTER 4. |
INDUCTION, RECURSION AND RECURRENCES |
|||||||||
|
|
|
log2 n−1 |
|
|
log2 n−1 |
|
|
|||
|
= |
n |
|
|
log n − |
|
i |
+ n |
|
||
|
|
|
i=0 |
|
|
|
i=0 |
|
|
||
|
= |
n |
(log |
2 |
n)(log |
2 |
n) |
− |
(log2 n)(log2 n − 1) |
+ n |
|
|
|
|
|
|
|
|
2 |
|
|||
|
= |
O(n log2 n) . |
|
|
|
|
|
|
|||
A bit of mental arithmetic in the second last line of our equations shows that the log2 n will not cancel out, so our solution is in fact Θ(n log2 n).
4.6-4 Find the best big-O bound you can on the solution to the recurrence
T (n) = |
T (n/2) + n log n |
if n > 1 |
, |
1 |
if n = 1 |
assuming n is a power of 2. Is this bound a big-Θ bound?
The tree for this recurrence is
Problem Size |
Work |
n |
n |
n/2 |
n/2 log(n/2) |
|
|
log n |
|
levels |
|
n/4 |
n/4 log(n/4) |
n/8 |
n/8 log(n/8) |
2 |
2 log 2 |
Notice that the work done at the bottom nodes of the tree is determined by the statement T (1) = 1 in our recurrence, not by the recursive equation. Summing the work, we get
log2 n−1 n |
log |
n |
+ 1 = |
n |
||
i=0 |
2i |
2i |
||||
|
|
|
||||
|
|
|
|
|
||
|
|
|
|
= |
n |
|
|
|
|
|
≤ |
n |
|
log2 n−1 |
1 |
|
(log n − log 2i) |
+ 1 |
|||||
|
|
|
|
||||||
i=0 |
|
2i |
|||||||
|
|
|
|
|
|
|
|
|
|
log2 n−1 |
1 |
|
i |
|
|
||||
|
|
|
|
(log(n) − i) |
+ 1 |
||||
i=0 |
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
log2 n−1 |
1 |
i |
|
||||||
log n |
|
|
|
|
|
|
|
+ 1 |
|
i=0 |
2 |
|
|||||||
|
|
|
|||||||
|
|
|
|
|
|||||
≤ n(log n)(2) + 1 = O(n log n).
4.6. MORE GENERAL KINDS OF RECURRENCES |
131 |
In fact we have T (n) = Θ(n log n), because the largest term in the sum in our second line of equations is log(n), and none of the terms in the sum are negative. This means that n times the sum is at least n log n.
Removing Ceilings and Using Powers of b.
We showed that in our versions of the master theorem, we could ignore ceilings and assume our variables were powers of b. It might appear that these two theorems do not apply to the more general functions we have studied in this section any more than the master theorem does. However, they actually only depend on properties of the powers nc and not the three di erent kinds of cases, so it turns out we can extend them.
Notice that (xb)c = bcxc, and this proportionality holds for all values of x with constant of proportionality bc. Putting this just a bit less precisely, we can write (xb)c = O(xc). This suggests that we might be able to obtain Big-Θ bounds on T (n) when T satisfies a recurrence of the form
T (n) = aT (n/b) + f (n)
with f (nb) = Θ(f (n)), and we might be able to obtain Big-O bounds on T when T satisfies a recurrence of the form
T (n) ≤ aT (n/b) + f (n)
with f (nb) = O(f (n)). But are these conditions satisfied by any functions of practical interest? Yes. For example if f (x) = log(x), then
f (bx) = log(b) + log(x) = Θ(log(x)).
4.6-5 Show that if f (x) = x2 log x, then f (bx) = Θ(f (x)).
4.6-6 If f (x) = 3x and b = 2, is f (bx) = Θ(f (x))? Is f (b(x)) = O(f (x))?
Notice that if f (x) = x2 log x, then
f (bx) = (bx)2 log bx = b2x2(log b + log x) = Θ(x2 log x).
However, if f (x) = 3x, then
f (2x) = 32x = (3x)2 = 3x · 3x,
and there is no way that this can be less than or equal to a constant multiple of 3x, so it is neither Θ(3x) nor O(3x). Our exercises suggest the kinds of functions that satisfy the condition f (bx) = O(f (x)) might include at least some of the kinds of functions of x which arise in the study of algorithms. They certainly include the power functions and thus polynomial functions and root functions, or functions bounded by such functions.
There was one other property of power functions nc that we used implicitly in our discussions of removing floors and ceilings and assuming our variables were powers of b. Namely, if x > y (and c ≥ 0) then xc ≥ yc. A function f from the real numbers to the real numbers is called (weakly) increasing if whenever x > y, then f (x) ≥ f (y). Functions like f (x) = log x and f (x) = x log x are increasing functions. On the other hand, the function defined by
x if x is a power of b f (x) = x2 otherwise
is not increasing even though it does satisfy the condition f (bx) = Θ(x).
132 |
CHAPTER 4. INDUCTION, RECURSION AND RECURRENCES |
Theorem 4.6.1 Theorems 4.5.2 and 4.5.3 apply to recurrences in which the xc term is replaced by an increasing function for which f (bx) = Θ(f (x)).
Proof: We iterate the recurrences in the same way as in the proofs of the original theorems, and find that the condition f (x) = Θ(x) applied to an increasing function gives us enough information to again bound one the to one kind of recurrence above and below with a multiple of the other solution. The details are similar to those in the original proofs so we omit them. 
In fact there are versions of Theorems 4.5.2 and 4.5.3 for recurrence inequalities also. The proofs involve a similar analysis of iterated recurrences or recursion trees, and so we omit them.
Theorem 4.6.2 Let a and b be positive real numbers with b > 2 and let f : R+ → R+ be an increasing function such that f (bx) = O(f (x)). Then every solution t(x) to the recurrence
t(x) |
≤ |
at(x/b) + f (x) |
if x ≥ b |
, |
||
|
c |
if 1 |
≤ |
x < b |
|
|
|
|
|
||||
where a, b, and c are constants, satisfies t(x) = O(h(x)) if and only if every solution T (x) to the recurrence
T (n) ≤ |
aT (n/b) + f (n) |
if n > 10 |
, |
d |
if n = 1 |
where n is restricted to powers of b, satisfies T (n) = O(h(n)).
Theorem 4.6.3 Let a and b be positive real numbers with b ≥ 2 and let f : R+ → R+ be an increasing function such that f (bx) = O(f (x)). Then every solution T (n) to the recurrence
T (n) |
≤ |
at( n/b ) + f (n) |
if n > 1 |
, |
|
d |
if n = 1 |
|
satisfies T (n) = O(h(n)) if and only if every solution t(x) to the recurrence
t(x) |
≤ |
aT (x/b) + f (x) |
if x ≥ b |
, |
||
|
d |
if 1 |
≤ |
x < b |
|
|
|
|
|
||||
satisfies t(x) = O(h(x)).
Problems
1. (a) Find the best big-O upper bound you can to any solution to the recurrence
T (n) = |
4T (n/2) + n log n |
if n > 1 |
1 |
if n = 1 . |
(b)Assuming that you were able to guess the result yougot in part (a), prove, by induction, that your answer is correct.
2.Is the big-O upper bound in the previous exercise actually a big-Θ bound?
4.6. MORE GENERAL KINDS OF RECURRENCES |
133 |
||
3. Show by induction that |
|
|
|
T (n) = |
8T (n/2) + n log n |
if n > 1 |
|
d |
if n = 1 |
||
|
|||
has T (n) = O(n3) for any solution T (n).
4.Is the big-O upper bound in the previous problem actually a big-Θ upper bound?
5.Show by induction that any solution to a recurrence of the form
T (n) ≤ 2T (n/3) + c log3 n
is O(n log3 n). What happens if you replace 2 by 3 (explain why)? Would it make a di erence if we used a di erent base for the logarithm (only an intuitive explanation is needed here).
6.What happens if you replace the 2 in the previous exercise by 4? What if you replace the log3 by logb? (Use recursion trees.)
7.Give an example (di erent from any in the text) of a function for which f (bx) = O(f (x)). Give an example (di erent from any in the text) of a function for which f (bx) is not O(f (x)).
8.Give the best big O upper bound for the recurrence T (n) = 2T (n/3 − 3) + n, and then prove by induction that your upper bound is correct.
9.Find the best big-O upper bound you can to any solution to the recurrence defined on nonnegative integer powers of two by
T (n) ≤ 2T ( n/2 + 1) + cn.
Prove, by induction, that your answer is correct.

134 |
CHAPTER 4. INDUCTION, RECURSION AND RECURRENCES |
4.7Recurrences and Selection
One common problem that arises in algorithms is that of selection. In this problem you are given n distinct data items from some set which has an underlying order. That is, given any two items, it makes sense to talk about one being smaller than another. Given these n items, and some value i, 1 ≤ i ≤ n, you wish to find the ith smallest item in the set. For example in the set {3, 1, 8, 6, 4, 11, 7}, the first smallest (i = 1) is 1, the third smallest (i = 3) is 4 and the seventh smallest (i = n = 7) is 11. An important special case is that of finding the median, which is the case of i = n/2 .
4.7-1 How do you find the minimum (i = 1) or maximum (i = n) in a set? What is the running time? How do you find the second smallest? Does this approach extend to finding the ith smallest? What is the running time?
4.7-2 Give the fastest algorithm you can to find the median (i = n/2 ).
In Exercise 4.7-1, the simple O(n) algorithm of going through the list and keeping track of the minimum value seen so far will su ce to find the minimum. Similarly, if we want to find the second smallest, we can go through the list once, find the smallest, remove it and then find the smallest in the new list. This also takes O(n) time. However, if we extend this to finding the ith smallest, the algorithm will take O(in) time. Thus for finding the median, it takes O(n2) time.
A better idea for finding the median is to first sort the items, and then take the item in position n/2. Since we can sort in O(n log n) time, this algorithm will take O(n log n) time. Thus if i = O(log n) we might want to run the algorithm of the previous paragraph, and otherwise run this algorithm. 2
All these approaches, when applied to the median, take at least some multiple of (n log n) units of time. 3 As you know, the best sorting algorithms take O(n log n) time also. As you may not know, there is actually a sense in which one can prove every comparison-based sorting algorithm takes Ω(n log n) time This raises the natural question of whether it is possible to do selection any faster than sorting. In other words, is the problem of finding the median element of a set significantly easier than the problem of ordering (sorting) the whole set.
Recursive Selection Algorithm
Suppose for a minute that we magically knew how to find the median in O(n) time. That is, we have a routine MagicMedian, that given as input a set A, returns the median. We could then use this in a divide and conquer algorithm for Select as follows;
Select(A, i, n)
(selects the ith smallest element in set A, where n = |A|) if (n = 1)
return the one item in A
2We also note that the running time can be improved to O(n + i log n) by first creating a heap, which takes O(n) time, and then performing a Delete-Min operation i times.
3An alternate notation for f (x) = O(g(x)) is g(x) = Ω(f (x)). Notice the change in roles of f and g. In this notation, we say that all of these algorithms take Ω(n log n) time.

4.7. RECURRENCES AND SELECTION |
135 |
else
p = M agicM edian(A)
Let H be the set of elements greater than p
Let L be the set of elements less than or equal to p if (i ≤ |L|)
Return Select(L, i, |L|)
else
Return Select(H, i − |L|, |H|)
By H we do not mean the elements that come after p in the list, but the elements of the list which are larger than p in the underlying ordering of our set. This algorithm is based on the following simple observation. If we could divide the set A up into a ”lower half” (L) and an ”upper” half (H), then we know which of these two sets the ith smallest element in A will be in. Namely, if i ≤ n/2 , it will be in L, and otherwise it will be in H. Thus, we can recursively look in one or the other set. We can easily partition the data into two sets by making two passes, in the first we copy the numbers smaller than p into L, and in the second we copy the numbers larger than p into H. 4
The only additional detail is that if we look in H, then instead of looking for the ith smallest, we look for the i − n/2 th smallest, as H is formed by removing the n/2 smallest elements from A. We can express the running time by the following recurrence:
T (n) ≤ T (n/2) + cn |
(4.22) |
From the master theorem, we know any function which satisfies this recurrence has T (n) = O(n).
So we can conclude that if we already know how to find the median in linear time, we can design a divide and conquer algorithm that will solve the selection problem in linear time. This is nothing to write home about (yet)!
Sometimes a knowledge of solving recurrences can help us design algorithms. First, let’s consider what recurrences have only solutions T (n) with T (n) = O(n). In particular, consider recurrences of the form T (n) ≤ T (n/b) + cn, and ask when they have solution T (n) = O(n). Using the master theorem, we see that as long as logb 1 < 1 (and since logb 1 = 0 for any b, this means than any b allowed by the master theorem works; that is, any b > 1 will work), all solutions to this recurrence will have T (n) = O(n). (Note that b does not have to be an integer.) Interpreting this as an abstract algorithm, and letting b = 1/b, this says that as long as we can solve a problem of size n by first solving (recursively) a problem of size b n, for any b < 1, and then doing O(n) additional work, our algorithm will run in O(n) time. Interpreting this in the selection problem, it says that as long as we can, in O(n) time, choose p to ensure that both L and H have size at most b n, we will have a linear time algorithm. In particular, suppose that, in O(n) time, we can choose p to ensure that both L and H have size at most (3/4)n. Then we will be able to solve the selection problem in linear time.
Now suppose instead of a MagicMedian box, we have a much weaker Magic Box, one which only guarantees that it will return some number in the middle half. That is, it will return a number that is guaranteed to be somewhere between the n/4th smallest number and the 3n/4th smallest number. We will call this box a MagicMiddle box, and can use it in the following algorithm:
4We can do this more e ciently, and “in place”, using the partition algorithm of quicksort.

136 |
CHAPTER 4. INDUCTION, RECURSION AND RECURRENCES |
Select1(A,i,n)
(selects the ith smallest element in set A, where n = |A| ) if (n = 1)
return the one item in A
else
p = M agicM iddle(A)
Let H be the set of elements greater than p
Let L be the set of elements less than or equal to p if (i ≤ |L|)
Return Select1(L, i, |L|)
else
Return Select1(H, i − |L|, |H|)
The algorithm Select1 is similar to Select. The only di erence is that p is now only guaranteed to be in the middle half. Now, when we recurse, the decision of the set on which to recurse is based on whether i is less than or equal to |L|.
This is progress, as we now don’t need to assume that we can find the median in order to have a linear time algorithm, we only need to assume that we can find one number in the middle half of the set. This seems like a much simpler problem, and in fact it is. Thus our knowledge of which recurrences solve to O(n) led us towards a more plausible algorithm.
Unfortunately, we don’t know a straightforward way to even find an item in the middle half. We will now describe a way to find it, however, in which we select a subset of the numbers and then recursively find the median of that subset.
More precisely consider the following algorithm (in which we assume that |A| is a multiple of
5.)
MagicMiddle(A) Let n = |A|
if (n < 60)
return the median of A
else
Break A into k = n/5 groups of size 5, G1, . . . , Gk for i = 1 to k
find mi, the median of Gi
Let M = {m1, . . . , mk } return Select1 (M, k/2 , k)
In this algorithm, we break A into n/5 sets of size 5, and then find the median of each set. We then (using Select1 recursively) find the median of medians and return this as our p.
Lemma 4.7.1 The value returned by MagicMiddle(A) is in the middle half of A.
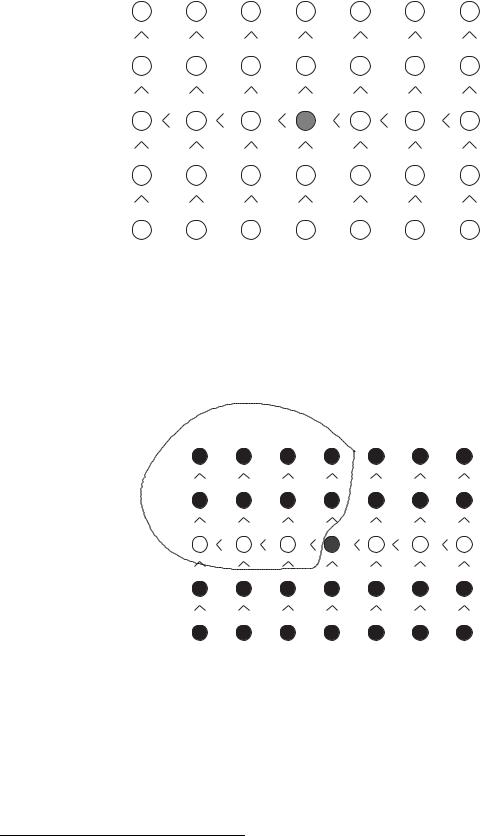
Proof: Consider arranging the elements in the following manner. For each set of 5, list them in sorted order, with the smallest element on top. Then line up all n/5 of these lists, ordered by their medians, smallest on the left. We get the following picture:
4.7. RECURRENCES AND SELECTION |
137 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
In this picture, the medians are in white, the median of medians is cross-hatched, and we have put in all the inequalities that we know from the ordering information that we have. Now, consider how many items are less than or equal to the median of medians. Every smaller median is clearly less than the median of medians and, in its 5 element set, the elements smaller than the median are also smaller than the median of medians. Thus we can circle a set of elements that is guaranteed to be smaller than the median of medians.
In one fewer than half the columns, we have circled 3 elements and in one column we have circled 2 elements. Therefore, we have circled at least5
1 |
n |
− 1 3 + 2 = |
3n |
− 1 |
||
2 |
|
5 |
10 |
|
||
elements.
So far we have assumed n is an exact multiple of 5, but we will be using this idea in circumstances when it is not. If it is not an exact multiple of 5, we will have n/5 columns (in
5We say “at least” because our argument applies exactly when n is even, but underestimates the number of circled elements when n is odd.
138 |
CHAPTER 4. INDUCTION, RECURSION AND RECURRENCES |
particular more than n/5 columns), but in one of them we might have only one element. It is possible that column is one of the ones we counted on for 3 elements, so our estimate could be two elements too large. 6 Thus we have circled at least
310n − 1 − 2 = 310n − 3
elements. It is a straightforward argument with inequalities that as long as n ≥ 60, this quantity is at least n/4. So if at least n/4 items are guaranteed to be less than the median, then at most 3n/4 items can be greater than the median, and hence |H| ≤ 3n/4.
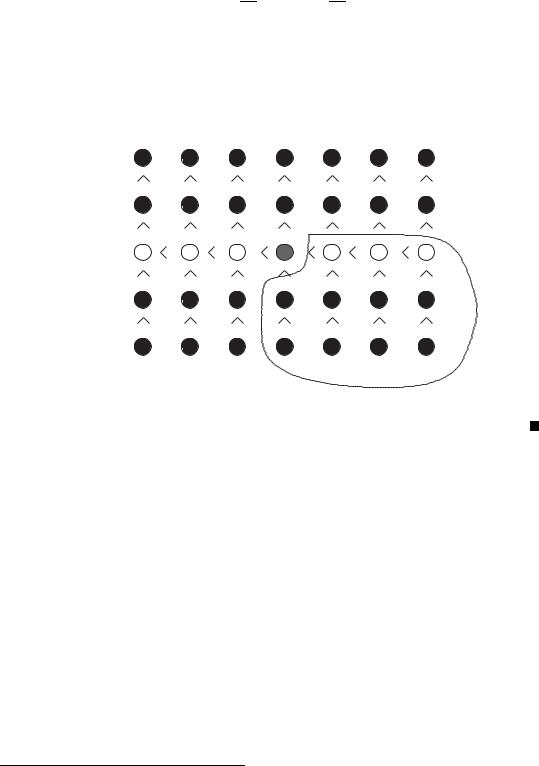
We can make the same argument about larger elements. A set of elements that is guaranteed to be larger than the median of medians is circled in the picture below:
By the same argument as above, this shows that the size of L is at most 3n/4.
Note that we don’t actually identify all the nodes that are guaranteed to be, say, less than the median of medians, we are just guaranteed that the proper number exists.
Since we only have the guarantee that MagicMiddle gives us an element in the middle half of the set if the set has at least sixty elements, we modify Select1 to start out by checking to see if n < 60, and sorting the set to find the element in position i if n < 60. Since 60 is a constant, this takes a constant amount of time.
4.7-3 Let T (n) be the running time of Select1 on n items. What is the running time of Magic Middle?
4.7-4 What is a recurrence for the running time of Select1?
4.7-5 Can you prove by induction that each solution to the recurrence for Select1 is O(n)?
The first step of MagicMiddle is to divide the items into sets of five; this takes O(n) time. We then have to find the median of each set. There are n/5 sets and we spend O(1) time per set, so the total time is O(n). Next we recursively call Select1 to find the median of medians;
6A bit less than 2 because we have more than n/5 columns.
4.7. RECURRENCES AND SELECTION |
139 |
this takes T (n/5) time. Finally, we do the partition of A into those elements less than or equal to the “magic middle” and those that are not. This too takes O(n) time. Thus the total running time is T (n/5) + O(n).
Now Select1 has to call Magic Middle and then recurse on either L or H, each of which has size at most 3n/4. Adding in a base case to cover sets of size less than 60, we get the following recurrence for the running time of Select1:
T (n) |
≤ |
T (3n/4) + T (n/5) + O(n) |
if n ≥ 60 |
(4.23) |
|
O(1) |
if n < 60 |
|
We can now verify by induction that T (n) = O(n). What we want to prove is that there is a constant k such that T (n) ≤ kn. What the recurrence tells us is that there are constants c and d such that T (n) ≤ T (3n/4) + T (n/5) + cn if n ≥ 60, and otherwise T (n) ≤ d. For the base case we have T (n) ≤ d ≤ dn for n < 60, so we choose k to be at least d and then T (n) ≤ kn for n < 60. We now assume that n ≥ 60 and T (m) ≤ km for values m < n, and get
T (n) ≤ T (3n/4) + T (n/5) + cn
≤ 3kn/4 + 2kn/5 + cn
=19/20kn + cn
=kn + (c − k/20)n .
As long as k ≥ 20c, this is at most kn; so we simply choose k this big and by the principle of mathematical induction, we have T (n) < kn for all positive integers n.
Uneven Divisions
This kind of recurrence is actually an instance of a more general class which we will now explore.
4.7-6 We already know that every solution of T (n) = T (n/2) + O(n) satisfies T (n) = O(n). Use the master theorem to find Big-O bounds to all solutions of T (n) = T (cn) + O(n) for any constant c < 1.
4.7-7 Use the master theorem to find Big-O bounds to all solutions of T (n) = 2T (cn)+O(n) for any constant c < 1/2.
4.7-8 Suppose you have a recurrence of the form T (n) = T (an) + T (bn) + O(n) for some constants a and b. What conditions on a and b guarantee that all solutions to this recurrence all have T (n) = O(n)?
Using the master theorem, for Exercise 4.7-6, we get T (n) = O(n), since log1/c 1 < 1. We also get O(n) for Exercise 4.7-7, since log1/c 2 < 1 for c < 1/2. You might now guess that as long as a + b < 1, the recurrence T (n) = T (an) + T (bn) + O(n) has solution O(n). We will now see why this is the case.
First let’s return to the recurrence we had, T (n) = T (3/4n) + T (n/5) + O(n), and let’s try to draw a recursion tree. This doesn’t quite fit our model, as the two subproblems are unequal, but we will try to draw it anyway and see what happens.
