- •«Математическое моделирование в логистике»
- •2013 Содержание
- •Введение
- •1. Моделирование в логистике
- •1.1. Классификация моделей
- •1.2. Научная база логистики и методология
- •2. Многокритериальная оптимизация в логистике
- •2.1. Включение целевых функций в ограничения
- •2.2. Метод последовательных уступок (метод главного критерия)
- •2.3. Метод экспертных оценок. Непосредственное назначение коэффициентов веса.
- •2.4. Оценки точности параметров в баллах
- •2.5. Статистический метод экспертных оценок
- •2.6. Метод бинарных (парных) соотношений
- •3. Транспортная задача
- •, , ,.
- •4. Базовые понятия теории графов
- •5. Сетевое планирование и управление
- •5.1. Элементы сетевого графика
- •5.2. Временные параметры сетевого графика
- •6. Задачи прокладки коммуникаций
- •6.1. Прокладка коммуникаций
- •6.2. Планирование сети дорог
- •10 9,928... 9,196...
- •7. Задачи поиска оптимальных путей
- •8. Задачи размещения
- •8.1. Размещение регулярных пунктов обслуживания
- •8.2. Размещение экстренных пунктов обслуживания
- •9. Задачи объезда
- •9.1. Маршрут китайского почтальона
- •9.2. Маршрут коммивояжера
- •Вопросы для самоконтроля
- •Список использованной литературы
4. Базовые понятия теории графов
Граф G задается
множеством точек или вершин
![]() и множеством
линий
и множеством
линий
![]() ,
соединяющих
между собой все или часть этих точек.
Сокращенная запись имеет вид
,
соединяющих
между собой все или часть этих точек.
Сокращенная запись имеет вид
![]() .
.
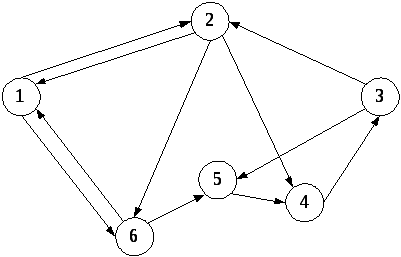
Ориентированные
графы (рис.
4.1,а): линии имеют направление и называются
дугами
![]() ,
где
,
где
![]() – исток,
– исток,![]() – сток.
– сток.
Неориентированные
графы (рис.
4.1,б): линии не имеют направления и
называются ребрами
![]() ,
где
,
где
![]() ,
,![]() – концевые
вершины.
– концевые
вершины.
Смешанные графы (рис. 4.1, в): часть линий имеет направление, часть – нет.
а)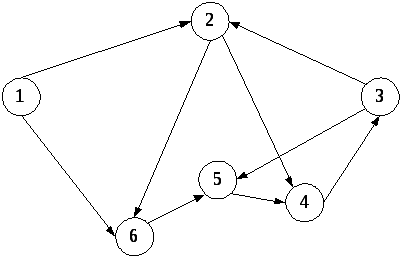
б)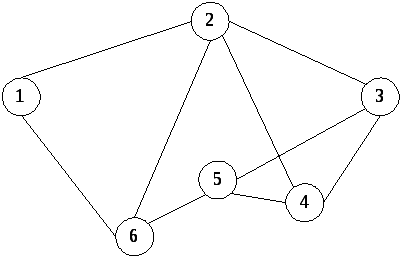
в)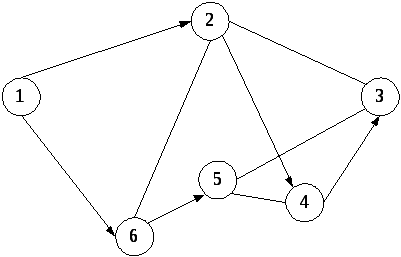
Рис. 4.1. Ориентированные и неориентированные графы
Мультиграфы:
имеются несколько парных ребер (рис.
4.2, а) или однонаправленных дуг (рис. 4.3,
а)
![]() ,
,![]() .
.
Псевдографы:
имеются ребра (рис. 4.2,б) или дуги (рис.
4.3,б) вида
![]() ,
которые называются петли.
,
которые называются петли.
Мульти-псевдографы: имеются парные ребра (рис. 4.2,в) или дуги (рис. 4.3,в), а также петли.
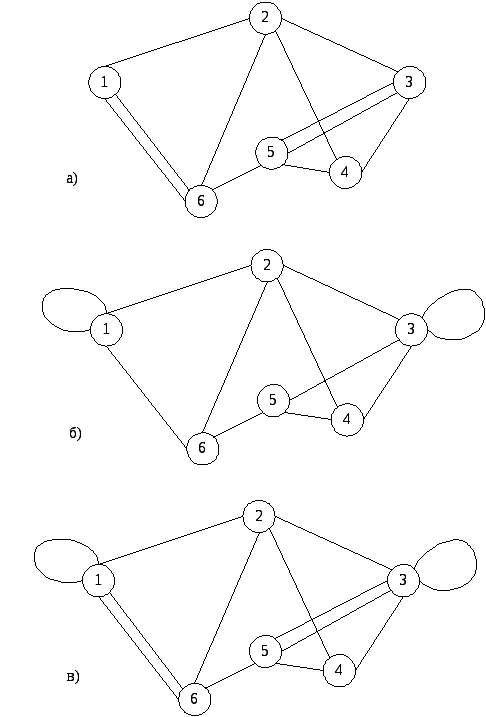
Рис. 4.2. Неориентированные мульти- и псевдографы
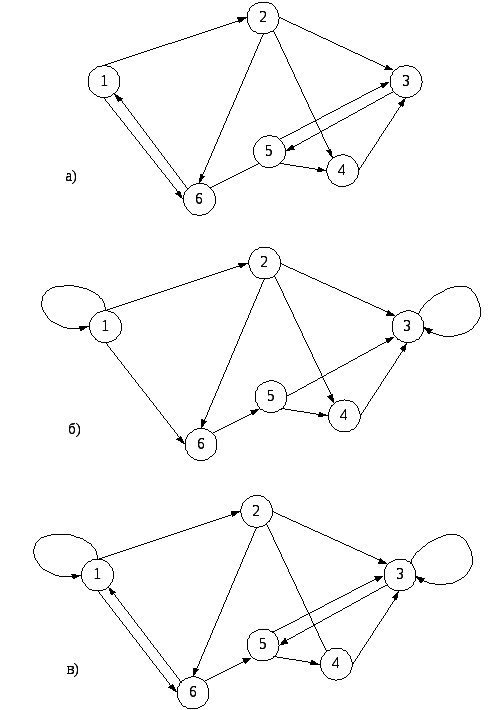
Рис. 4.3. Ориентированные мульти- и псевдографы
Способы задания графов:
1. Графический способ.
Связи между вершинами отображаются в виде линий (для неориентированных графов) или линий со стрелками (для ориентированных графов).
2. Матрица
смежности
![]() .
.

Матрицы смежности однозначно задают как неориентированные (в этом случае матрица симметрична относительно главной диагонали), так и ориентированные графы и смешанные графы.
Для смешанных графов эквивалентно выглядит задание ребра и пары разнонаправленных дуг. Никаких проблем не возникает с псевдографами (петле соответствует единица на главной диагонали), тогда как мультиграфы заданы быть не могут. В качестве примера зададим несколько графов при помощи матриц смежности.
Матрицы смежности для орграфа на рис. 4.1.,а
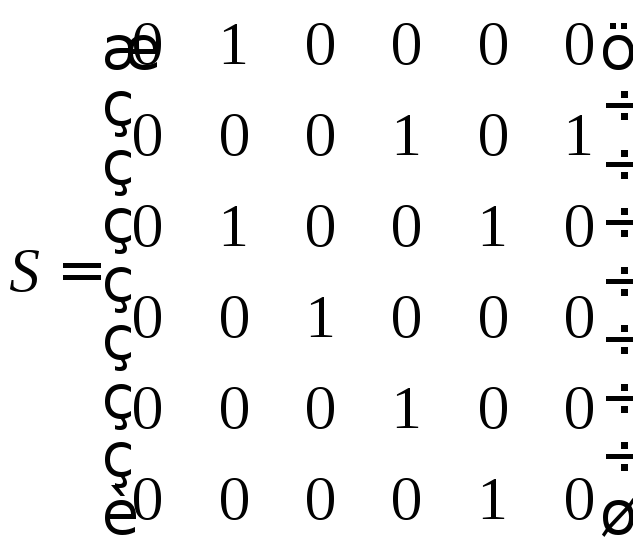 ,
,
для графа на рис. 4.2,б
 .
.
3. Матрица
инциденций
![]() .
.
Для ориентированных графов:

для неориентированных графов:

Матрицы инциденций
однозначно задают как неориентированные,
так и ориентированные графы. В принципе
нет никаких препятствий для задания
смешанных графов – в отличие от матрицы
смежности в этом случае задание ребра
и пары разнонаправленных дуг будет
отличаться. Никаких проблем не возникает
с мультиграфами (и в ориентированном и
в неориентированном случаях), а также
неориентированными псевдографами.
Неоднозначность возникает при задании
ориентированных псевдографов: на
пересечении строки, помеченной петлей,
и столбца, помеченного вершиной, на
которой эта петли присутствует, по
правилу должны одновременно находиться
как 1 так и
![]() .
Из этой ситуации имеется выход – вместо
одной матрицы
.
Из этой ситуации имеется выход – вместо
одной матрицы
![]() граф задается двумя матрицами – матрицей
истоков
граф задается двумя матрицами – матрицей
истоков
![]() и матрицей стоков
и матрицей стоков
![]() :
:
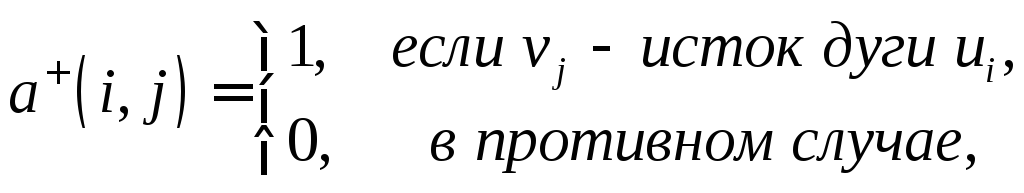

В качестве примера зададим несколько графов при помощи матриц инциденций.
Матрицы инциденций для орграфа на рис. 4.1.,а
 ,
,
для графа на рис. 4.2,б
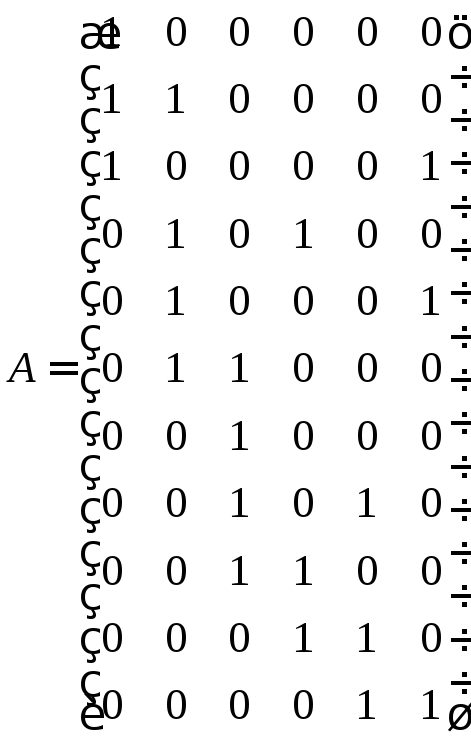 .
.
4. Функциональное
представление
![]() и
и![]() :
:
![]() ,
если существует дуга
,
если существует дуга
![]() ;
;
![]() ,
если существует дуга
,
если существует дуга
![]() .
.
При помощи
функционального представления однозначно
задаются как неориентированные (в этом
случае
![]() ),
так и ориентированные и смешанные графы.
Как и в случае с матрицей смежности, для
смешанных графов эквивалентно выглядит
задание ребра и пары разнонаправленных
дуг. Никаких проблем не возникает с
псевдографами (если вершина
),
так и ориентированные и смешанные графы.
Как и в случае с матрицей смежности, для
смешанных графов эквивалентно выглядит
задание ребра и пары разнонаправленных
дуг. Никаких проблем не возникает с
псевдографами (если вершина![]() имеет петлю, то и в
имеет петлю, то и в![]() ,
и в
,
и в![]() войдет вершина
войдет вершина![]() ).
Мультиграфы заданы быть не могут. В
качестве примера зададим при помощи
функционального представления:
).
Мультиграфы заданы быть не могут. В
качестве примера зададим при помощи
функционального представления:
орграф на рис. 4.1, а
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
граф на рис. 4.2, б
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Взвешенные графы
Иногда дугам или ребрам графа G сопоставляются (приписываются) числа, называемые весом, или длиной, или стоимостью (ценой) дуги или ребра. Тогда граф G называется графом со взвешенными дугами (ребрами). Иногда веса приписываются вершинам графа, и тогда получается граф со взвешенными вершинами. Если в графе веса приписаны и дугам, и вершинам, то он называется просто взвешенным.
Вес (длина,
стоимость) пути (маршрута)
![]() ,
представленного последовательностью
дуг (ребер)
,
представленного последовательностью
дуг (ребер)
![]() – число
– число![]() ,
равное сумме весов всех дуг (ребер),
входящих в путь (маршрут). Причем если
дуга (ребро) входит в него несколько
раз, соответствующий вес также учитывается
многократно.
,
равное сумме весов всех дуг (ребер),
входящих в путь (маршрут). Причем если
дуга (ребро) входит в него несколько
раз, соответствующий вес также учитывается
многократно.
Базовые определения
|
Неориентированные графы
|
Ориентированные графы
|
|
Петля – ребро, начальная и конечная вершины которого совпадают. |
Петля – дуга, начальная и конечная вершины которой совпадают. |
|
Смежные вершины – вершины, соединенные ребром. |
Смежные вершины – вершины, соединенные дугой. |
|
Смежные ребра – ребра, имеющие общие концевые вершины. |
Смежные дуги – дуги, имеющие общие концевые вершины. |
|
Степень
вершины
|
Полустепенъ
исхода (захода)
вершины
|
|
Маршрут – последовательность ребер, в которой конечная вершина всякого ребра, отличного от последнего, является начальной вершиной следующего. |
Путь (или ориентированный маршрут) – последовательность дуг, в которой конечная вершина всякой дуги, отличной от последней, является начальной вершиной следующей. |
|
Цепь – маршрут, в котором каждое ребро используется не больше одного раза. |
Ориентированная цепь (или орцепь) – путь, в котором каждая дуга используется не больше одного раза. |
|
Простая цепь – маршрут, в котором каждая вершина используется не более одного раза. |
Простая орцепь – путь, в котором каждая вершина используется не более одного раза. |
|
Замкнутый маршрут (цикл) – маршрут, в котором начальная вершина является конечной. |
Замкнутый путь (орцикл) – путь, в котором начальная вершина первой дуги совпадает с конечной вершиной последней дуги. |
|
Простой цикл – замкнутый маршрут, в котором одна и та же вершина используется только один раз (за исключением начальной и конечной вершин, которые совпадают). |
Простой орцикл (контур) – замкнутый путь, в котором одна и та же вершина используется только один раз (за исключением начальной и конечной вершин, которые совпадают). |
|
Неориентированные графы |
Ориентированные графы |
|
Гамильтонов цикл – простой цикл, проходящий через все вершины графа. |
Гамильтонов цикл – контур, проходящий через все вершины графа. |
|
Эйлеров цикл – замкнутая цепь, проходящая через все ребра графа. |
Эйлеров цикл – замкнутая орцепь, проходящая через все дуги графа. |
|
Связный граф – граф, в котором для любой пары вершин существует маршрут. Иначе – граф несвязный. | |
|
|
Сильно
связный граф –
граф, в котором для любой пары вершин
|