2.2 Регістри
Здвигові регістри являють собою схему, що складається зі зв'язаних між собою однобітових елементів пам'яті, розташованих в одному корпусі, цей корпус називається інтегральна схема.
Елементи пам'яті є тригери з'єднані один з одним таким чином, що вихід одного служить входом іншого. Входи-виходи регістра здвигу організовані параллельно – послідовно. Використається для тимчасового зберігання даних, і перетворення даних з паралельної в послідовну форму й навпаки. Кількість тригерів визначається розрядністю числа.
Розрізняють:
- здвигові регістри зі зрушенням вправо;
- здвигові регістри зі зрушенням уліво;
- реверсивні здвигові регістри.
У
своїй роботі я буду використати трьох
розрядний реверсивний регістр здвигу.
Для реалізації даної схеми 
складаємо
функціональну таблицю автомата,
яка знаходиться
в таблиці 2.2.1.
Таблиця 2.2.1- функціональна таблиця трьох розрядного реверсивного регістру здвигу
|
A |
X |
t |
t+1 |
Тригери |
Z1 |
Z2 |
Z3 | |||||||||
|
Y1 |
Y2 |
Y3 |
Y1 |
Y2 |
Y3 |
Ys1 |
Yr1 |
Ys2 |
Yr2 |
Ys3 |
Yr3 | |||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
~ |
0 |
~ |
0 |
~ |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
~ |
0 |
~ |
0 |
1 |
0 |
0 |
1 |
|
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
~ |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
|
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
~ |
0 |
1 |
~ |
0 |
0 |
1 |
1 |
|
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
~ |
1 |
0 |
0 |
|
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
|
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
~ |
0 |
1 |
0 |
1 |
1 |
0 |
|
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
~ |
0 |
~ |
0 |
1 |
1 |
1 |
|
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
~ |
0 |
~ |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
~ |
0 |
1 |
0 |
0 |
1 |
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
~ |
0 |
0 |
1 |
1 |
|
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
~ |
0 |
1 |
0 |
0 |
~ |
1 |
0 |
0 |
|
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
~ |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
|
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
~ |
0 |
~ |
0 |
1 |
0 |
1 |
1 |
0 |
|
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
~ |
0 |
~ |
0 |
~ |
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
~ |
0 |
~ |
0 |
~ |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
~ |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
|
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
~ |
0 |
1 |
0 |
|
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
~ |
0 |
0 |
1 |
0 |
1 |
1 |
|
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
~ |
0 |
~ |
1 |
0 |
0 |
|
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
~ |
0 |
0 |
1 |
0 |
~ |
1 |
1 |
0 |
|
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
~ |
0 |
~ |
0 |
0 |
1 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
~ |
0 |
~ |
1 |
0 |
0 |
0 |
0 |
|
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
~ |
1 |
0 |
~ |
0 |
0 |
0 |
1 |
|
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
~ |
0 |
~ |
0 |
0 |
1 |
1 |
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
~ |
1 |
0 |
1 |
0 |
0 |
|
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
~ |
0 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
~ |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
~ |
0 |
~ |
0 |
~ |
0 |
1 |
1 |
1 |
Згідно таблиці 2.2.1 будуємо карти Карно, і отримуємо функцію для кожного входу кожного тригеру.
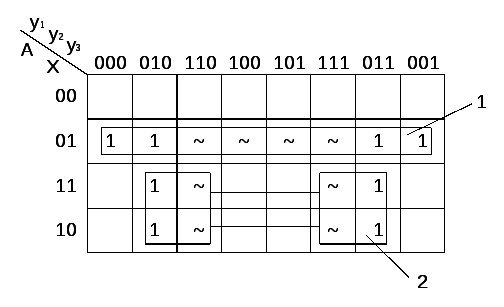
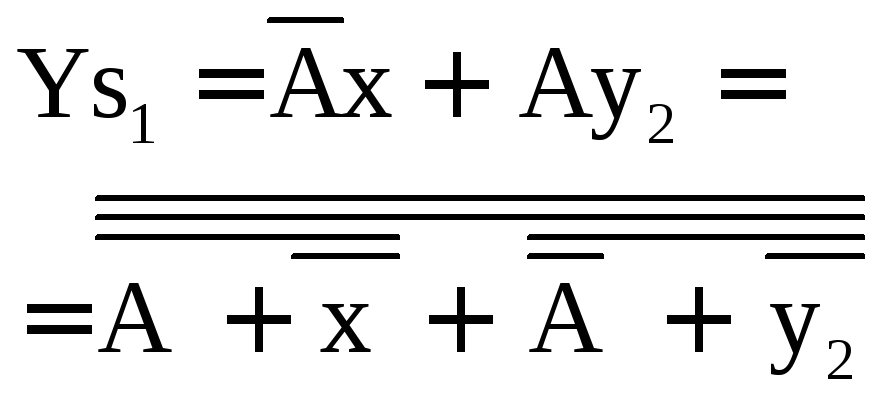
рис. 2.2.1
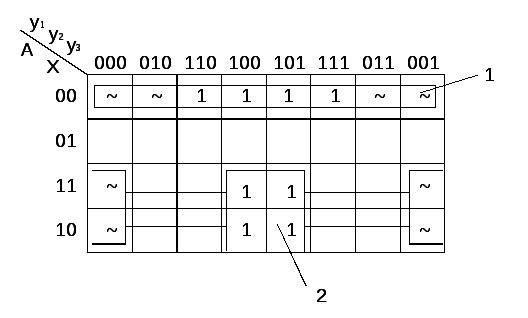
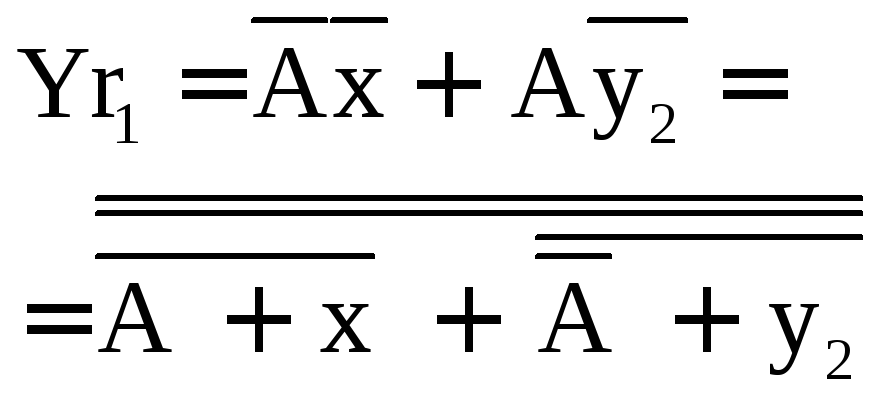
рис. 2.2.2
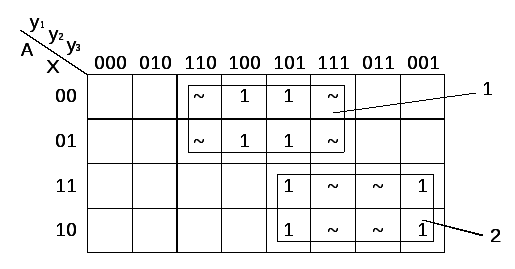
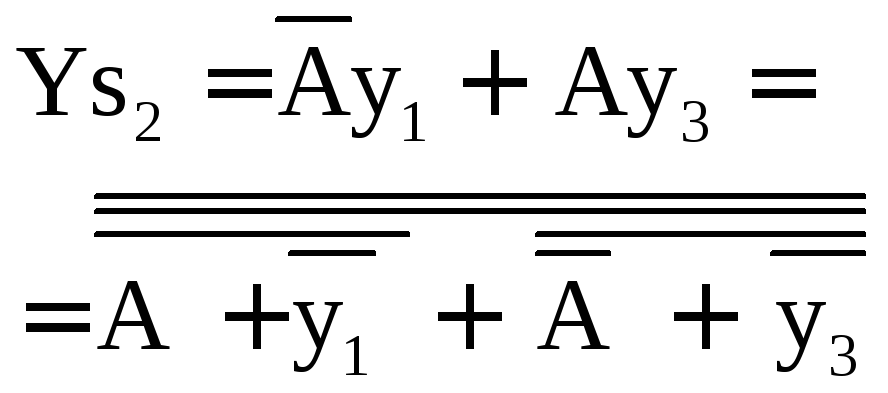
рис. 2.2.3
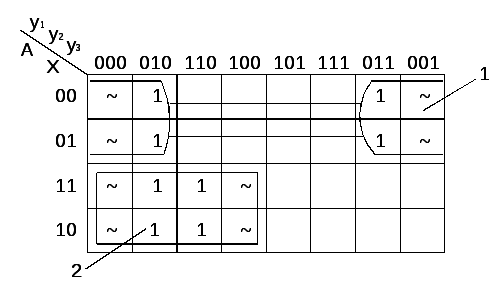
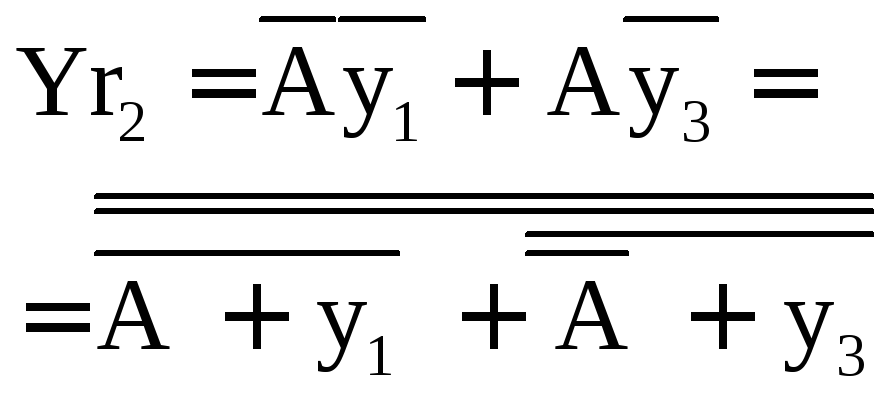
рис. 2.2.4
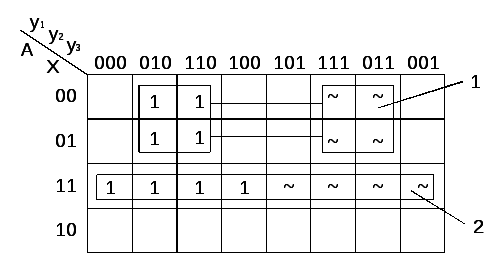
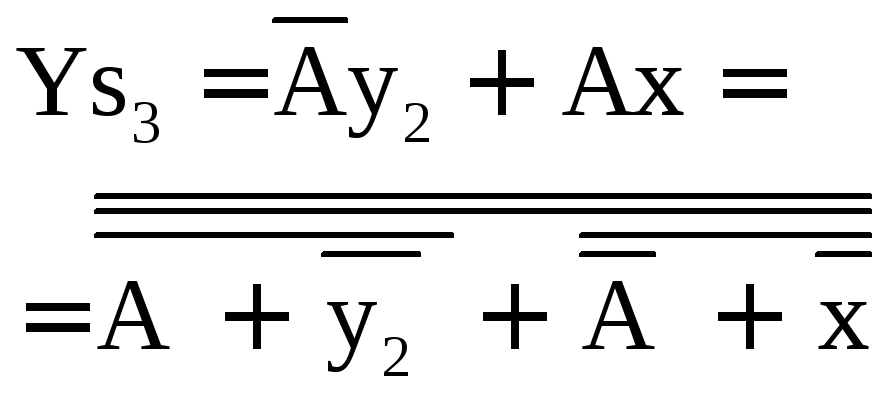
рис. 2.2.5
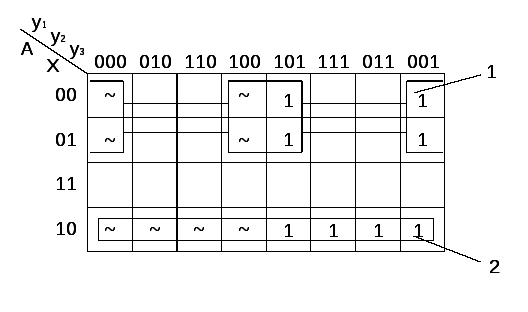
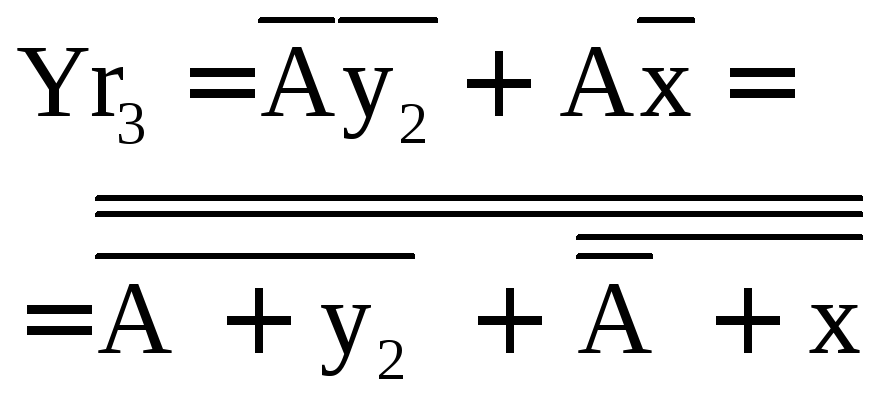
рис. 2.2.6
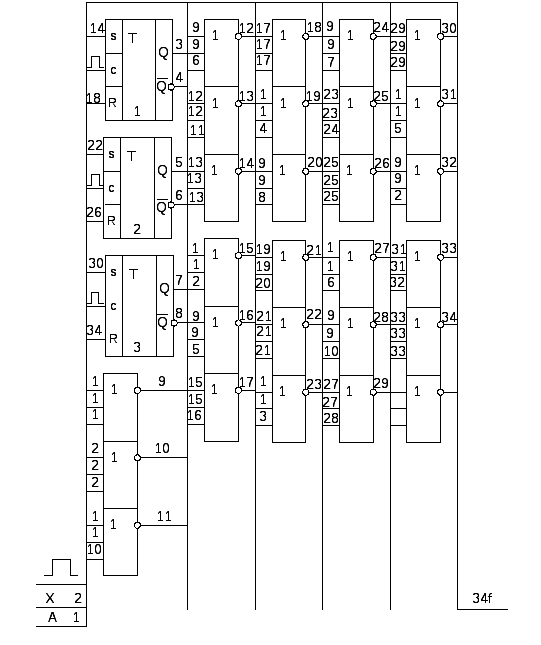
Рис. 2.2.7 – схема трьох розрядного реверсивного регістру здвигу