1.2Синтез функції, заданої аналітичним способом на комутаторах
Комутатором (мультиплексором) називається комбінаційний пристрій, що має
декілька
входів і один вихід, призначене для
комутації в бажаному порядку сигналів
з декількох вхідних шин на одну вихідну.
Завдяки мультиплексора здійснюється
тимчасове розділення інформації, що
поступає по різних каналах.
Входи мультиплексора діляться на інформаційні, адресні та стробуючі . На інформаційні входи подається інформація, що передається на вихід
мультиплексора. Адресні входи допомагають вибирати потрібний інформаційний вхід, а на стробуючий вхід подається стробуючий сигнал, що вирішує підключення вибраного входу на один загальний або залежно від
конструкції комутатора на два вихода.
Кількість інформаційних та адресних входів взаємозв'язане. Якщо число
адресних входів n, то число інформаційних входів 2n, а стробуючий вхід, як
правило, один. За відсутності стробуючого сигналу, тобто С=0, а в деяких мультиплексорах при С=1 зв'язок між інформаційними входами і виходом відсутній.
Наявність стробуючого входу дозволяє синхронізувати роботу мультиплексора з роботою інших вузлів, а також нарощувати його розрядність.
Нижче приведена таблиця роботи любого комутатора
Таблиця 1.2
-
Адресні входи
Вхід синхронізації
Вихід
А0
А1
З
Q
-
-
0
0
0
0
1
B0
1
0
1
B1
0
1
1
B2
1
1
1
B3
Залежно від кількості інформаційних входів розрізняють
комутатори: К4-1, К8-1 і До 16-1. Умовне графічне позначення комутатора К4-1 приведене на мал.
Рисунок 1.5
Мультиплексори
можуть використовуватися не тільки як
комутатори, але і для інших цілей. Одна
з перспективних областей їх використання
- реалізація комбінаційних, а у ряді
випадків і логічних схем. На мультиплексорах
можна реалізувати будь-яку логічну
функцію, що містить до n+
1 змінною,
де n
- число
адресних входів.
У курсовій роботі необхідно реалізувати функцію, задану аналітичним способом, залежну від п'яти змінних. Задану функцію можна побачити вище.
Синтез комбінаційних схем за допомогою комутаторів проводиться із декількох операцій, а саме:
Скласти таблицю істинності перед тим треба спростити ф-ю, якщо це треба. Моя таблиця істинності знаходиться на наступній сторінці.
Щоб реалізації на чотирьох комутаторах К4-1 функції п'яти незалежних змінних необхідно:
на адресні входи подати сигнал А1 = Х3 та А0 = Х4
на інформаційні входи треба подати сигнал який випливає із
комбінації стовпців Х5 та F цей стовбець в моєї таблиці названий В.
П
риклад
комбінацій Х5
та F:
сигнали стробуючий вхід
Таблиця1.3
|
|
F |
В |
|
0 |
0 |
0 |
|
0 |
1 | |
|
1 |
1 |
1 |
|
0 |
1 | |
|
0 |
1 |
|
|
0 |
1 | |
|
1 |
0 |
|
|
0 |
1 |
Для заповнення таблиці 1.2.3 треба вихідну ф-ю спростити, перетворити:
F
9=
Х1Х4+ Х1(Х5+ Х2Х3)
= Х1+ Х4+ Х1Х5Х2Х3= Х1+ Х4+ Х1(
Х5Х2 +Х5Х3)=
=
Х1+Х4+Х1Х5Х2+Х1Х5Х3=
Х1(Х2+Х2)(Х3+Х3)(Х4+Х4)(Х5+Х5)
+ (Х1+Х1)(Х2+Х2)(Х3+Х3)
Х
4(Х5+Х5)
+ Х1Х2(Х3+Х3)(Х4+Х4)Х5
+ Х1(Х2+Х2)Х3(Х4+Х4)Х5=
Х
1(Х2Х3+
Х2Х3+ Х2Х3+
Х2Х3)(Х4Х5+ Х4Х5+
Х4Х5+ Х4Х5) +
Х1Х2(Х3Х4+ Х3Х4+
Х3Х4+
+
Х3Х4)Х5+ (Х1Х2+ Х1Х2+ Х1Х2+
Х1Х2)(Х3Х5+ Х3Х5+
Х3Х5+ Х3Х5)Х4 +
Х1Х3Х5(Х2Х4+
+
Х2Х4+
Х2Х4+Х2Х4) =
=
Х1Х2Х3Х4Х5+
Х1Х2Х3Х4Х5+
Х1Х2Х3Х4Х5+
Х1Х2Х3Х4Х5+
Х1Х2Х3Х4Х5+
Х1Х2Х3Х4Х5+
+
Х1Х2Х3Х4Х5+
Х1Х2Х3Х4Х5+
Х1Х2Х3Х4Х5+
Х1Х2Х3Х4Х5+
Х1Х2Х3Х4Х5+
Х1Х2Х3Х4Х5+
+
Х1Х2Х3Х4Х5+
Х1Х2Х3Х4Х5+
Х1Х2Х3Х4Х5+
Х1Х2Х3Х4Х5+
Х1Х2Х3Х4Х5+
Х1Х2Х3Х4Х5+
+
Х1Х2Х3Х4Х5+
Х1Х2Х3Х4Х5+
Х1Х2Х3Х4Х5+
Х1Х2Х3Х4Х5+
Х1Х2Х3Х4Х5+
Х1Х2Х3Х4Х5+
+
Х1Х2Х3Х4Х5+
Х1Х2Х3Х4Х5+
Х1Х2Х3Х4Х5+
Х1Х2Х3Х4Х5+
Х1Х2Х3Х4Х5+
Х1Х2Х3Х4Х5+
+
Х1Х2Х3Х4Х5+
Х1Х2Х3Х4Х5+
Х1Х2Х3Х4Х5+
Х1Х2Х3Х4Х5+
Х1Х2Х3Х4Х5+
Х1Х2Х3Х4Х5+
+
Х1Х2Х3Х4Х5+
Х1Х2Х3Х4Х5+
Х1Х2Х3Х4Х5+
Х1Х2Х3Х4Х5.
Fсднф
= Х1Х2Х3Х4Х5
+ Х1Х2Х3Х4Х5
+Х1Х2Х3Х4Х5
+Х1Х2Х3Х4Х5
+Х1Х2Х3Х4Х5
+
+
Х1Х2Х3Х4Х5
+ Х1Х2Х3Х4Х5
+ Х1Х2Х3Х4Х5
+ Х1Х2Х3Х4Х5
+Х1Х2Х3Х4Х5
+
+
Х1Х2Х3Х4Х5
+ Х1Х2Х3Х4Х5
+ Х1Х2Х3Х4Х5
+ Х1Х2Х3Х4Х5
+Х1Х2Х3Х4Х5
+
+
Х1Х2Х3Х4Х5
+ Х1Х2Х3Х4Х5
+ Х1Х2Х3Х4Х5
+ Х1Х2Х3Х4Х5
+Х1Х2Х3Х4Х5
+
+
Х1Х2Х3Х4Х5
+ Х1Х2Х3Х4Х5
+ Х1Х2Х3Х4Х5
+ Х1Х2Х3Х4Х5
+Х1Х2Х3Х4Х5
+
+
Х1Х2Х3Х4Х5
+ Х1Х2Х3Х4Х5.
Будуємо талицю істиності
Таблиця 1.4
|
№ |
Х1 |
Х2 |
Х3 |
Х4 |
Х5 |
F |
B | |
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
В0 |
1 |
|
1 |
0 |
0 |
0 |
0 |
1 |
1 | ||
|
2 |
0 |
0 |
0 |
1 |
0 |
1 |
В1 |
1 |
|
3 |
0 |
0 |
0 |
1 |
1 |
1 | ||
|
4 |
0 |
0 |
1 |
0 |
0 |
1 |
В2 |
1 |
|
5 |
0 |
0 |
1 |
0 |
1 |
1 | ||
|
6 |
0 |
0 |
1 |
1 |
0 |
1 |
В3 |
1 |
|
7 |
0 |
0 |
1 |
1 |
1 |
1 | ||
|
8 |
0 |
1 |
0 |
0 |
0 |
1 |
В0' |
1 |
|
9 |
0 |
1 |
0 |
0 |
1 |
1 | ||
|
10 |
0 |
1 |
0 |
1 |
0 |
1 |
В1' |
1 |
|
11 |
0 |
1 |
0 |
1 |
1 |
1 | ||
|
12 |
0 |
1 |
1 |
0 |
0 |
1 |
В2' |
1 |
|
13 |
0 |
1 |
1 |
0 |
1 |
1 | ||
|
14 |
0 |
1 |
1 |
1 |
0 |
1 |
В3' |
1 |
|
15 |
0 |
1 |
1 |
1 |
1 |
1 | ||
|
16 |
1 |
0 |
0 |
0 |
0 |
1 |
В0'' |
|
|
17 |
1 |
0 |
0 |
0 |
1 |
0 | ||
|
№ |
Х1 |
Х2 |
Х3 |
Х4 |
Х5 |
F |
B | |
|
18 |
1 |
0 |
0 |
1 |
0 |
1 |
В1" |
1 |
|
19 |
1 |
0 |
0 |
1 |
1 |
1 | ||
|
20 |
1 |
0 |
1 |
0 |
0 |
1 |
В2'' |
|
|
|
1 |
0 |
1 |
0 |
1 |
0 | ||
|
22 |
1 |
0 |
1 |
1 |
0 |
1 |
В3" |
1 |
|
23 |
1 |
0 |
1 |
1 |
1 |
1 | ||
|
24 |
1 |
1 |
0 |
0 |
0 |
1 |
В0''' |
|
|
25 |
1 |
1 |
0 |
0 |
1 |
0 | ||
|
26 |
1 |
1 |
0 |
1 |
0 |
1 |
В1"' |
1 |
|
27 |
1 |
1 |
0 |
1 |
1 |
1 | ||
|
28 |
1 |
1 |
1 |
0 |
0 |
0 |
В2"' |
0 |
|
29 |
1 |
1 |
1 |
0 |
1 |
0 | ||
|
30 |
1 |
1 |
1 |
1 |
0 |
1 |
В3"' |
1 |
|
31 |
1 |
1 |
1 |
1 |
1 |
1 | ||
21
Роботу комутаторів можна показати таблицею істинності. Ця таблиця істиності показує які сигнали треба подавати строби комутаторів і в ній показано коли включається перший другий ітд. Входи.
Таблиця 1.5
|
X1 |
X2 |
C1 |
C2 |
C3 |
C4 |
|
0 |
0 |
1 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
0 |
1 |
В нашій роботі треба побудувати схему за допомогою комутатора 555КП1,
Тепер будуємо схему комутаторів із загальною шиною.
Рисунок1.6
Побудувавши схему на 4-х комутаторах будуємо схему із 5-ти комутаторів.
На стробуючий вхід комутаторів подаємо сигнал «0».
На інформаційні входи 4-х комутаторів подаємо значення із стовпця В, а на інформаційні входи 5-го ком-ра подаємо виходи із перших 4-х ком.
На управляючі входи 1-х 4-х подаемо сигнал Х3 та Х4 а на 5-й ком. подаємо Х1 та Х2.
Інвертні виходи з ком. інвертуємо і отримуємо прямий сигнал.
Нижче
приводжу малюнок із загальною шиною
5-ти комутаторів.
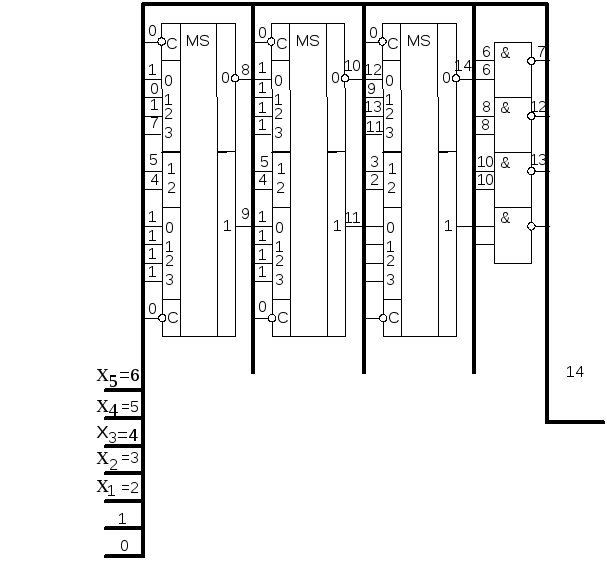
Рисунок1.7