Васильев

Тема: Основы моделирования. Линейное программирование.

5. В суточный рацион включают два продукта питания П1 и П2, причем продукта П1 должно войти в дневной рацион не более 200 ед. Стоимость 1 ед. продукта П1 составляет 2 р., про­дукта П2 — 4р. Содержание питательных веществ в 1 ед. про­дукта, минимальные нормы потребления указаны в табл.

Питательные вещества	Минимальная норма потребления	Содержание питательных веществ в 1 ед. продукта
		П1	П2
A	120	0.2	0.2
B	160	0.4	0.2

Определить оптимальный рацион питания, стоимость ко­торого будет наименьшей.

l. этап: Анализ условия задачи.

Все количественные данные можно записать в виде таблицы

ll. этап: Обозначаю неизвестные величины.

Обозначим через х1 и х2 количество единиц продуктов П1 и П2 которое войдёт в дневной рацион.

III. этап: Cоставляю систему ограничений

П1 и П2 не должно быть отрицательным

X1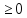 X2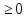

Известно также, количество продукта П1, которое должно войти в дневной рацион ограничен X1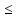200

По условию его количество должно быть больше или равно 120, то есть имеем ещё ограничение: 0.2*X1+0.2.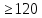

Аналогичное используя минимальные нормы потребления вещества В получим ограничение  0.4*X1+0.2*X2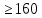

IV. этап: Составляю целевую функцию.

Учитывая, стоимость продуктов должна быть минимальной, целевая функция задачи будет иметь вид:

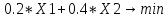
Математическая модель:

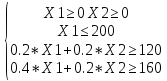
V. этап: Графическое решение задачи

На полуплоскости изображаются неравенства, выраженные из ограничений:

x	y1	y2
100	50	-700
90	75	-550
80	100	-400
70	125	-250
60	150	-100
50	175	50
40	200	200
30	225	350
20	250	500
10	275	650
0	300	800
-10	325	950
-20	350	1100
-30	375	1250
-40	400	1400

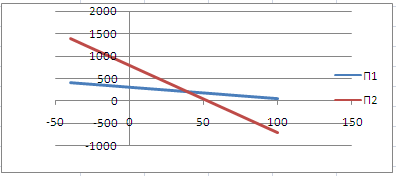
Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи. Анализ графического решения???

VI. этап: Применяю «Поиск решения» для определения:

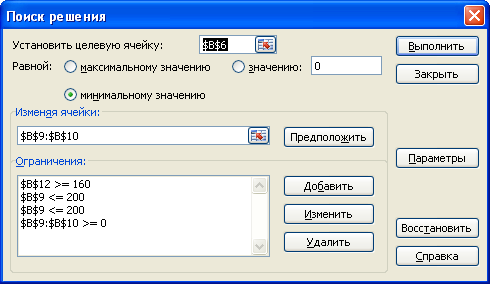
Результат:

Прямая Z(x) = const пересекает область в точке D. Так как точка D получена в результате пересечения прямых (а) и (б), то ее координаты удовлетворяют уравнениям этих прямых:

X1=200 0,2x1+0,2x2=120

Решив систему уравнений, получим: x1 = 200, x2 = 400

Откуда найдем минимальное значение целевой функции:

Z=2*200+4*400=400+1600=2000р.

Ответ: Для получения минимальной стоимости рациона необходимо в суточный рацион включить 200 ед. продукта П1 и 400 ед. продукта П2 , при этом стоимость будет наименьшей 2000р. Графическое решение и решение Поиском решений совпадают?????

Вывод: Изучил основные понятия математического моделирования, линейного программирования. Получил навыки построения математических моделей.