-
Метод касательных (Ньютона).
Тема: Решение нелинейного уравнения методом касательных (Ньютона).
Постановка
задачи:
Найти корень нелинейного уравнения
методом
касательных с точностью
.
Краткая
теория:
Дано нелинейное уравнение F(x)
=0,
где функция у
= F(x)
определена и непрерывно-дифференцируема
для всех
,
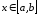причем функция меняет знак на концах
этого отрезка т.е. F(a)
·
F(b)
<
0.
Приближенное решение ξ ; и погрешность приближения Δξ; находятся по следующей схеме:
если
F(b)
·
F"(x)
> 0 на [a,b],
то
;
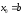если
F(a)
·
F"(x)
> 0 на [a,b],
то
;
,
.
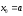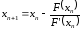Приближенное решение ξ, и погрешность приближения Δξ:
,
.
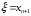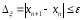Блок-схемы:
Отделение корней Метод касательных
Текст программы:
Program Metod_Kasateln;
Const Eps=0.0001; H=0.25;
Var alfa,beta,X,dX, x1,x2,y1,y2:Real; k:integer;
Function F(xf:Real):Real;
Begin
F:=Cos(xf-1)-Sqr(xf)/3
End;
Function dF(Xf:Real):Real;
Begin
dF:=-Sin(xf-1)-2/3*xf
End;
Function d2F(x1,x2:Real):Real;
Function ddF(xf:Real):Real;
Begin
ddF:=-Cos(xf-1)-2/3
End;
Var s:Real;
Begin
S:=0;
While x1<=x2 do
Begin
S:=S+ddF(x1);
x1:=x1+H/2;
End;
d2F:=S;
End;
Procedure M_Kas(a,b:Real; Var Xn,dX1:Real;var k:integer);
Var Xn1:Real;
Begin
If F(a)*d2F(a,b)>0
Then Xn:=a
Else Xn:=b;
dX1:=1;
While Abs(dx1)>EPS do
Begin
Xn1:=Xn;
Xn:=Xn1-F(Xn1)/dF(Xn1);
dX1:=Xn1-Xn; inc(k);
End;
End;
Begin {Отделение корней}
Write('Введите промежуток : '); ReadLn(Alfa,Beta);
x1:=alfa;
x2:=x1+H;
y1:=F(x1);
While x2<=beta do
Begin
y2:=F(x2);
If y1*y2<=0
Then
Begin
WriteLn('Корень определен на промежутке ( ',x1:0:2,' ; ',x2:0:2,' )');
M_Kas(x1,x2,X,dX,k);
WriteLn('X = ',X:10:8,' +- ',dX:10:8); WriteLn(‘Количество итерации=’,k);
End;
If y1*y2=0
Then
Begin
x2:=x2+H; y2:=F(x2);
End;
x1:=x2; x2:=x1+H; y1:=y2;
End;
If X=0 Then WriteLn('На этом промежутке корней НЕ СУЩЕСТВУЕТ.');
End.
Тестовый пример:
Найти
корень нелинейного уравнения
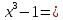0
x1=1.00.
Второй и третий корень мнимый.
Введите промежуток : -5 5
Корень определен на промежутке ( 1.00 ; 1.10 )
X = 1.00000001 +- -0.00000768
Количество итерации=5
Протокол:
Проверка и вывод
Проверка и вывод:
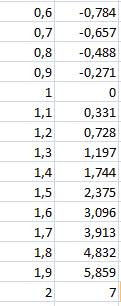
Решение
задачи:
0.
График уравнения:
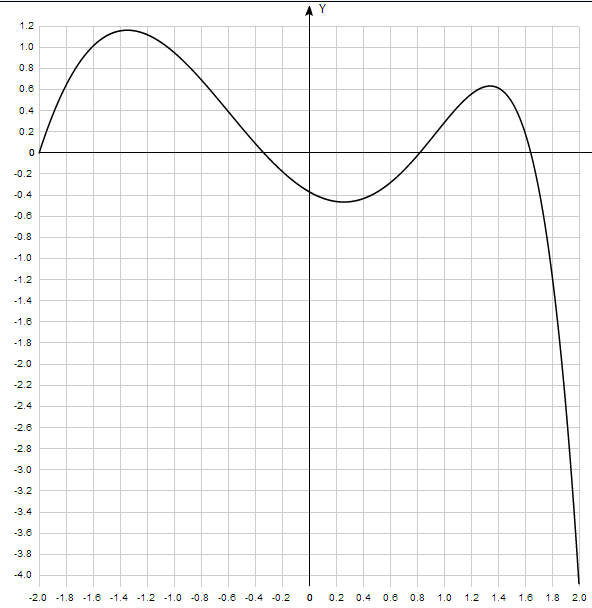
Протокол:
Введите промежуток: -5 5
Корень определен на промежутке (-2.0 ;-1.90)
X = -1.99830693 +- 0.00000000
Количество итерации=3
Корень определен на промежутке (-0.4 ;-0.3)
X = -0.33600869 +- -0.00001653
Количество итерации=4
Корень определен на промежутке (0.8;0.9)
X = 0.820235501 +- 0.00000031
Количество итерации=5
Корень определен на промежутке (1.6;1.7)
X = 1.64271501 +- 0.000005
Количество итерации=4
Отделим
корни уравнения графически (и программно).
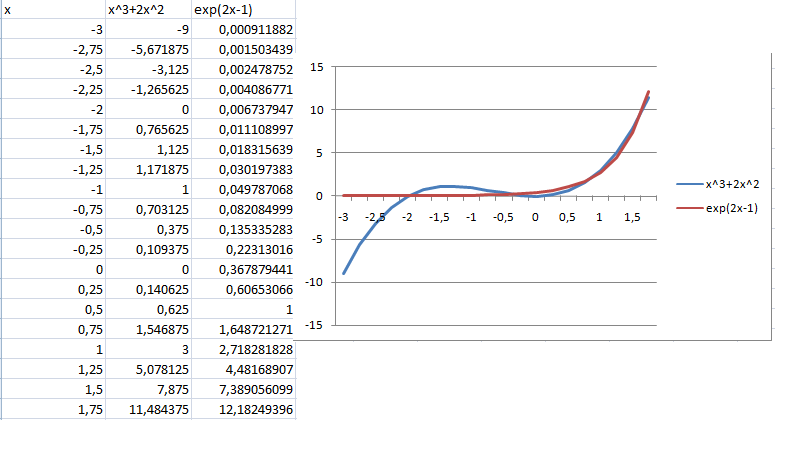
Для этого построим график функци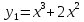и
и
и найдем абсциссы точек пересечения
графиков этих функций:
.
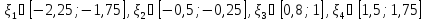Проверка и вывод:
В качестве примера рассмотрим первый и второй корень.
Уточним корни методом касательных:
1)
.
Для этого определим знаки функции
и второй её производной
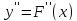на этом отрезке [-2,25;-1,75].
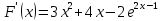
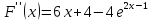
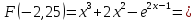-9,000911882<0
,
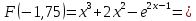0,754516003>0
.
Тогда
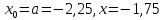
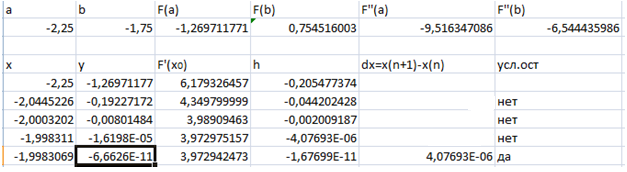
Применяем
формулу
.
Оценим
погрешность приближения. Так как
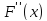не меняет свой знак на данном отрезке,
то
достигает своего наибольшего и наименьшего
значения на концах отрезка [-2,25;-1,75],
поэтому
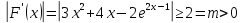для любого
.
Тогда используя оценку погрешности
для
любого
.
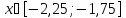Получим
,
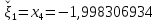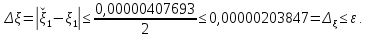
Следовательно, приближенное значение первого корня равно
.
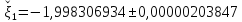Запишем приближенное значение корня только верными значащими цифрами в узком смысле.
.
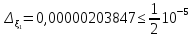
Округлим
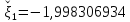до
.
Получим
,
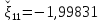с погрешностью округления
.
.
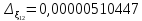Найдем
число верных знаков для
.
.
.
.
.
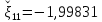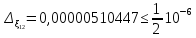
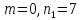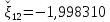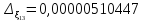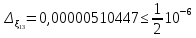
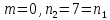Следовательно
.
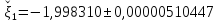Ответ:
2)
.
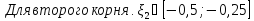Для
этого определим знаки функции
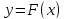и второй её производной
на этом отрезке
.
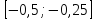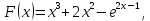
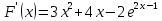
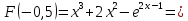0,239664717>0
-0,11375516<0
.
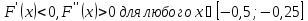Тогда
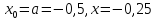
Применяем
формулу
.
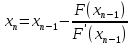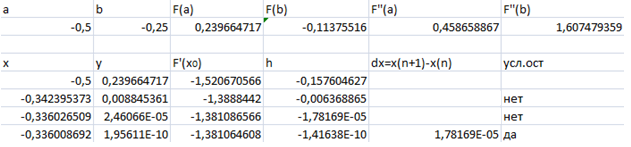
Оценим
погрешность приближения. Так как
не меняет свой знак на данном отрезке,
то
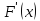достигает своего наибольшего и наименьшего
значения на концах отрезка
,
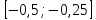поэтому
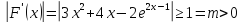для любого
.
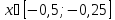Тогда используя оценку погрешности
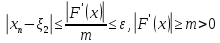для
любого
.
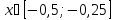Получим
,
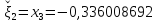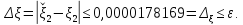
Следовательно, приближенное значение второго корня равно
.
Запишем приближенное значение корня только верными значащими цифрами в узком смысле.
.
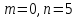Округлим
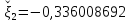до
.
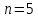Получим
,
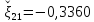с погрешностью округления
.
.
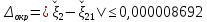Найдем
число верных знаков для
.
.
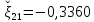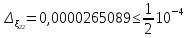
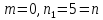Следовательно
.
Ответ: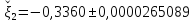
.